Artículo

 

Pronóstico de concentraciones máximas diarias de ozono: caso estación SEMAPA, Red MoniCA

 

 

Marcelo Gorritty Portillo

Coordinación de Post Grado en Ingeniería Sanitaria y Ambiental - CPISA
Universidad Mayor de San Andrés - UMSA Av. Mcal. Santa Cruz N° 1175, Casilla 10772, La Paz, Bolivia

e-mail: mgorritty@americatextil.com

 

 

---

Resumen

Se describen los resultados preliminares en el desarrollo de modelos de pronóstico de las concentraciones máximas diarias de ozono troposférico mediante el empleo de técnicas de regresión lineal múltiple. Los datos provienen de la Red MoniCA del municipio de Cercado, Cochabamba, para una estación de monitoreo automático ubicada en SEMAPA. Se desarrollan procedimientos de filtración de datos y un análisis de estacionalidad para los mismos. Los modelos utilizan mediciones de variables meteorológicas obtenidas en el sitio y son además validados estadísticamente. Se obtienen resultados para dos grupos de datos estacionales trimestrales y un grupo de datos semestral, los cuales son comparados con un modelo de persistencia.

Palabras clave: Ozono, pronóstico, modelos estadísticos, regresión.

---

 

 

1    Introducción

Cerca de la superficie de la tierra y en especial a nivel urbano, el ozono (O₃) se convierte en un contaminante tóxico y altamente reactivo. Desde varias décadas atrás, se han venido desarrollando estudios [3][8] que han generado técnicas de predicción de las concentraciones de contaminantes atmosféricos y que han sido implementadas paulatinamente en sistemas de alerta e información de la calidad del aire para áreas densamente pobladas. Actualmente, se cuentan con sistemas de pronóstico de la calidad del aire en diversas ciudades del mundo que emplean modelos avanzados de predicción en base a datos disponibles, en especial sobre variables meteorológicas o concentraciones de contaminantes primarios en algunos casos.

Por sus características, los modelos de pronóstico resultan altamente dependientes del sitio geográfico en especial por su relación con variables meteorológicas. No existe ninguna garantía que modelos utilizados en otras regiones puedan ser extrapolados más allá de las condiciones en las que fueron desarrollados [16]. Se presentan en este documento, resultados preliminares de un primer intento en el desarrollo de modelos de pronóstico de concentraciones máximas diarias de ozono, siendo el alcance específico los datos de concentraciones de ozono y mediciones de variables meteorológicas de la estación de monitoreo automático de SEMAPA [1][2], perteneciente a la Red MoniCa del municipio del Cercado de la ciudad de Cochabamba.

Existe una gran cantidad de modelos de pronóstico, aceptándose en general una amplia clasificación referida a modelos de regresión, series de tiempo y valores extremos [16][14]. Es de nuestro interés para el presente trabajo utilizar modelos de regresión, como una primera aproximación, dejando los otros modelos a futuros trabajos bajo esta línea de investigación. Se deja la última referencia para una descripción más detallada de los mismos.

La más familiar de las metodologías empleadas en la literatura revisada se refiere a la regresión lineal. En su forma más simple, los modelos de regresión lineal múltiple son usados para enlazar las concentraciones del contaminante atmosférico con variables meteorológicas del lugar [6].

La alta dependencia de la calidad de los modelos con la calidad de los datos, ha llevado, en el presente trabajo, a seleccionar cuidadosamente los mismos aunque se cuenta con una limitación en la cantidad de ellos. Se ha tomado en cuenta el periodo de datos desde agosto 2003 a julio 2005 para la estación automática de SEMAPA, la cual cuenta con un analizador de O₃ de radiación UV y mediciones a intervalos de muestreo de 15 min. [1]. Si bien se encuentran estudios con datos obtenidos en un rango de tiempo de hasta 10 años [15], el rango utilizado se considera suficiente para una primera aproximación en el análisis de modelos a corto plazo (modelos que se utilizan en la predicción de datos para algunos meses del año en base a un análisis estacional).

El modelo clásico de persistencia (O_3,t+1=O_3,t), es utilizado como base de comparación de los modelos de regresión. Los modelos son evaluados y comparados utilizando subconjuntos de los datos que no han sido empleados en el desarrollo de los mismos.

 

2    Metodología

2.1 Tratamiento de datos

La estación de monitoreo automático ubicada en SEMAPA, genera 96 datos al día con intervalos de 15 minutos para concentraciones de O₃ además de datos de radiación solar (RAD), humedad relativa (HR), temperatura (T), velocidad del viento (WS) y dirección del viento (WD), registrándose además el día juliano (DJ) y la fecha. Debido a la configuración en el almacenamiento de datos, los mismos no se mantienen en una base de datos única sino que se encuentran disponibles en archivos ordenados por fechas de almacenamiento. El rango de datos confiables disponibles se remonta a junio del 2003 para el caso del ozono, y agosto del mismo año para las variables meteorológicas, aunque la estación ha estado operando desde un par de años antes. A fin de contar con una base de datos consistente, los registros de los archivos se someten a un proceso inicial de filtración descrito como sigue.

2.1.1 Filtración primaria

Inicialmente, los datos se transfieren a una sola base bajo un mismo formato de almacenamiento. Como datos crudos, se encuentran en formato tipo texto. Se realiza una revisión detallada ya que son posibles tres tipos de error: a) error de operación, b) error de medición y c) error de almacenamiento.

El primer error se debe a datos perdidos por interrupción de la operación en la estación y abarca tanto a ozono como a variables meteorológicas al mismo tiempo. En el segundo tipo de error, el dato se presenta con valores nulos (NULL) o valores tipo NAN (not a number). Para el error tipo c) los datos presentan valores válidos pero se adjuntan caracteres extras o valores alfanuméricos que deben ser separados. Son parte del último tipo de error los datos que contienen mezcla de comas y puntos para la posición de los decimales.

2.1.2 Filtración Secundaria

Los datos almacenados en un solo conjunto de análisis son procesados para la búsqueda de valores negativos que no necesariamente se presentan para el ozono y las variables meteorológicas en los mismos días. Adicionalmente, se generan fechas para las variables meteorológicas ya que estas son almacenadas solamente con el día juliano respectivo y de modo inverso, se generan días julianos para los datos de ozono. En la generación de fechas y días julianos se emplean algoritmos desarrollados en MATLAB. Finalmente, para todos los datos, se transforman los valores del tiempo TIME en formato numérico ya que se emplean luego para análisis de frecuencias.

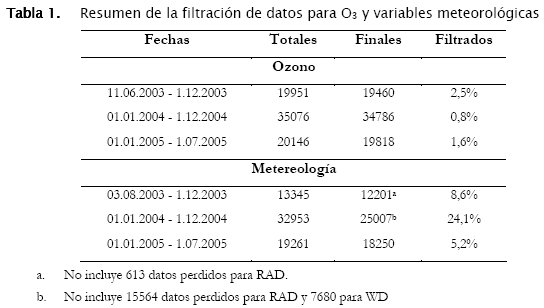
En la Tabla 1, se presenta el resumen de la filtración de datos. Las variables meteorológicas presentan un mayor porcentaje de filtración, en especial en el año 2004, con un 24.1% de los valores retirados.

Entre los datos iniciales de ozono y las variables meteorológicas existe además un desfase de prácticamente dos meses lo que induce a no contar con estos datos para el análisis de regresión. Los valores perdidos de RAD y WD mencionados al pie de la tabla no son considerados ya que, como se explica más adelante, no son variables con correlaciones estadísticamente significativas para el ozono.

2.2 Análisis de estacionalidad

En un procedimiento estadístico de regresión como el empleado en este trabajo, es de gran importancia tratar de estratificar un gran conjunto de datos en subconjuntos de análisis lo más homogéneos posible.

Aunque existen metodologías estadísticas para el análisis estadístico de conglomerados de datos [12][7] y su validación estacional, en el presente trabajo se utiliza una aproximación más simple referida al análisis de promedios horarios. La hipótesis se basa en que la variación climática típica de ciertos periodos anuales, se refleja también en una estacionalidad de los datos de ozono. Esta metodología es empleada en trabajos de referencia [10] y se explica por sí sola al visualizar en gráficos con escala horaria los valores de las variables promediadas según diferentes grupos de datos anuales.

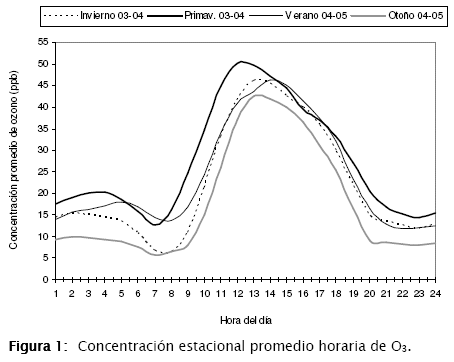
En este caso, se utilizan grupos de valores para la primavera 2003 y 2004, verano 2004 y 2005, otoño 2004 y 2005 e invierno 2003 y 2004. En la Figura 1, se muestran las concentraciones de ozono para los promedios horarios respecto a las estaciones del año. Puede observase una clara estacionalidad referida especialmente para la primavera y el otoño.

Los máximos se encuentran distribuidos alrededor del medio día. Las curvas muestran una fuerte estacionalidad en especial en las horas de la madrugada hasta pasado el medio día. En horas de la tarde las concentraciones tienden a ser más homogéneas. Está claro que por la estacionalidad observada, los modelos de pronóstico a corto plazo serán diferentes en especial para la primavera y el otoño.

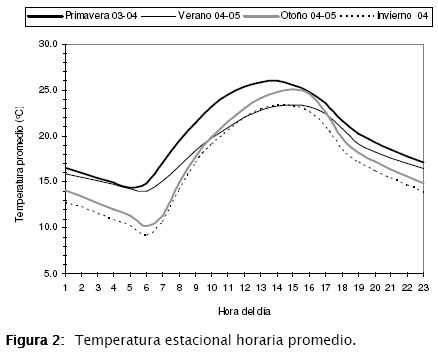
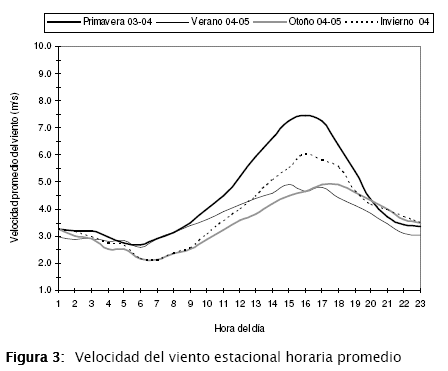
En las Figuras 2 y 3 se presentan los análisis de estacionalidad para la temperatura y la velocidad del viento.

 

En el caso de la temperatura, los valores obtenidos en primavera son más altos que los de verano para todas las horas del día a diferencia de lo que comúnmente se cree. Así mismo, las mayores concentraciones de ozono se presentan en primavera a pesar de que la dispersión es mayor debido a las mayores velocidades del viento mostradas en la Figura 3.

Los resultados mostrados sugieren que la estacionalidad en los datos de ozono está presente y que la generación de modelos de pronóstico debe respetar esta estacionalidad mientras no se cuente con mayor cantidad de datos anuales para generar un modelo a largo plazo. La EPA sugiere el uso de un mínimo de cuatro años de datos para el desarrollo de un modelo de persistencia [6].

2.3 Regresión Lineal Múltiple

Un análisis de regresión es un método que caracteriza las relaciones entre una variable respuesta Y, la cual se asume que es aleatoria, y una o más variables independientes. En un modelo de RLM, la expresión anterior asume la forma siguiente:

Bajo esta relación, existen supuestos importantes que no pueden ser violados de modo que el ajuste sea estadísticamente significativo: a) Y debe ser una variable aleatoria independiente con distribución normal, b) el término del error es una variable independiente y c) el término del error está normalmente distribuido.

Como primer paso, los conjuntos de datos de concentraciones máximas diarias de O₃ que se utilizan en el proceso de regresión, se validan en términos de su distribución normal. Para esto se utilizan procedimientos estadísticos disponibles en herramientas de software. Adicionalmente, es posible realizar una depuración de datos en términos de valores atípicos y diagramas de cajas, aunque estos valores se revisan cuidadosamente antes de eliminarlos ya que pueden no estar relacionados con problemas sistemáticos de medición. Se ha reportado [15] que una transformación logarítmica para los datos de ozono proporciona un mejor ajuste en términos de distribución normal, la cual se utiliza en los valores analizados.

A continuación, se deben seleccionar las variables independientes X_i más representativas sobre una relación lineal con la variable respuesta Y. En este punto, es común calcular la matriz de correlación del coeficiente de Pearson. Esta matriz contiene la correlación estadística, que mide la fuerza de la relación lineal entre las variables. Más allá de esto, está claro que la disponibilidad de datos es un primer criterio para seleccionar X_i. Para el caso que se describe, el conjunto de variables independientes está inicialmente descrito por WD, WS, T, HR y RAD. Es posible considerar además T_max que es la temperatura máxima diaria, [O₃]_max,t-1 la concentración máxima diaria de ozono del día anterior y T_max,_t-1 referida como T_max del día anterior [9].

Una vez definidas la variables predictoras, el procedimiento para el cálculo de los coeficientes β_i de la ecuación (1) obedece a un proceso de regresión de mínimos cuadrados. En este punto, los modelos de RLM se encuentran mucho más documentados que otro tipo de modelos y son ampliamente utilizados en otras disciplinas, por lo que existen herramientas de software que automatizan grandemente este proceso de cálculo.

Una medida natural de los efectos de las variables meteorológicas en el grado de ajuste del modelo es el coeficiente de determinación R². Mientras mayor sea éste, más satisfactorio es el ajuste del modelo a los datos. Sin embargo, debe existir un camino óptimo para decidir qué combinación de variables predictoras influyen más y mejor en el rendimiento del modelo. Para el caso que nos ocupa, se emplea el método escalonado de selección de variables o método stepwise. En este método, cada vez que se añade una nueva variable al modelo, se verifica que persista la importancia de todas las variables preexistentes.

Finalmente, se realiza una comprobación de los supuestos b) y c) mediante un análisis de los residuos, verificando la normalidad en la distribución de los mismos así como los coeficientes de auto correlación y de auto correlación parcial. Un estadístico adecuado para contrastar que las observaciones son independientes es el de Box-Lung [7].

2.4 Modelos de estudio

En base a la ecuación (1), un primer modelo a desarrollarse tiene la siguiente forma general:

Donde B_i se define estadísticamente como el estimado de β_i. De aquí en adelante se prescinde del uso del subíndice max.

Existe un segundo modelo [10] que obedece a la ley exponencial:

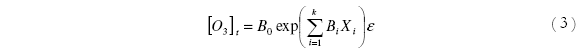
La transformación logarítmica presenta la siguiente ecuación:

Con el fin de comprobar el grado de ajuste de modelos lineales desarrollados bajo un enfoque fenomenológico, se estudian también los siguientes modelos:

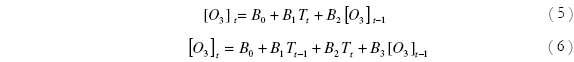
Las ecuaciones (5) y (6) son propuestas de Robeson & Stein [13] y Jorquera [9] respectivamente. En ambas ecuaciones, el término T se refiere a la temperatura máxima diaria. El subíndice t es el valor de la variable para el día del pronóstico y t-1 para el valor del día anterior.

Para el estudio de los modelos descritos, se utiliza el método escalonado para la determinación de los parámetros B_i en el caso de las ecuaciones (3) y (4). Para la regresión en base a las ecuaciones (5) y (6) no se emplea el método escalonado y en su lugar se introduce el modelo para su regresión tal como se lo propone.

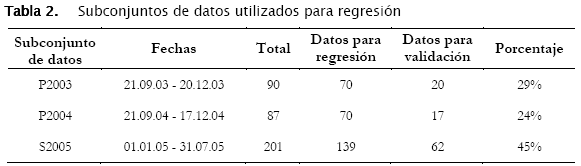
En la Tabla 2 se describen los subconjuntos de datos considerados en la regresión luego de aplicar un algoritmo para la determinación de los máximos diarios para el ozono y las variables meteorológicas.

Los subconjuntos de datos pertenecen a la primavera del 2003 y del 2004 y al primer semestre del 2005. Se recomienda un 25% de datos para la validación [6].

 

3    Resultados

3.1 Análisis de normalidad

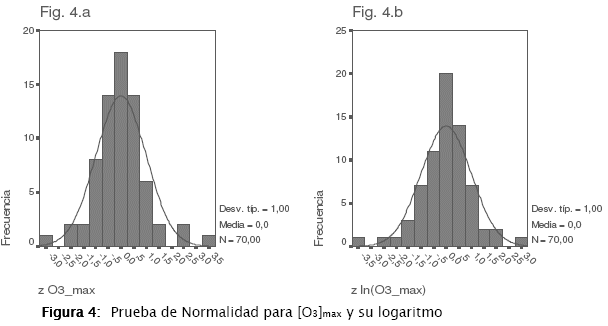
En la Figura 4 se muestran las distribuciones de frecuencias de las concentraciones máximas diarias de ozono normalizadas. La Fig. 4.b representa el logaritmo de la concentración de O₃ estandarizado con un coeficiente de asimetría de —0,356 que resulta menor al de la Fig. 4.a de 0,586, indicando una desviación menor a la Normal.

Las variables estandarizadas nos permiten realizar además un análisis de los percentiles. Si cualquiera de las distribuciones fuera Normal, teniendo en cuenta que la variable estandarizada tiene media 0 y desviación estándar 1, en el intervalo [-1,1] se concentraría aproximadamente el 69 por 100 de la distribución o, lo que es lo mismo, los percentiles 16 y 48 deberían coincidir con los valores -1 y 1. Para la Fig. 4.a y 4.b, estos valores son de [-0,8; 0,7] y [-0,8; 0,8]. El análisis se puede extender para los percentiles 2,5 y 97,5 bajo el rango [-2 , 2] que en esta caso dan [-2,3; 26] y [-2,7; 2,2] respectivamente.

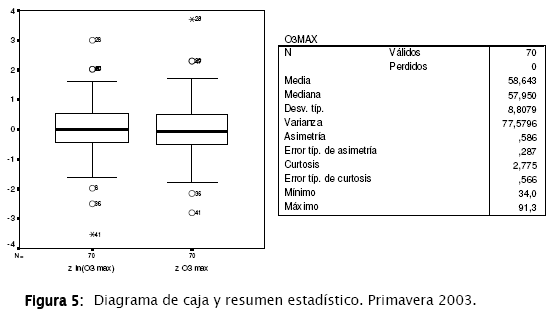
En la Figura 5 se muestra un diagrama de caja para la distribución de los datos atípicos y los datos extremos. Se puede ver una ligera asimetría para la variable estandarizada del O_3,max lo que confirma los resultados de la diferencia en el coeficiente.

Los valores atípicos se encuentran más de una vez y media el rango intercuartílico respecto de los límites superiores e inferiores de las cajas. Lo notorio en este caso es la presencia de datos extremos. Para la variable z O_3,max , el caso etiquetado como 28 corresponde a una lectura de 91,3 ppb (la media es de 58,6 ppb) identificado también como Máximo en el cuadro adjunto a la gráfica. Sin embargo, aunque aparece como un extremo, el dato no puede ser retirado ya que no hay indicios de una mala medición o un mal funcionamiento del equipo para esa fecha (esto se identifica en el procedimiento de filtrado anteriormente explicado).

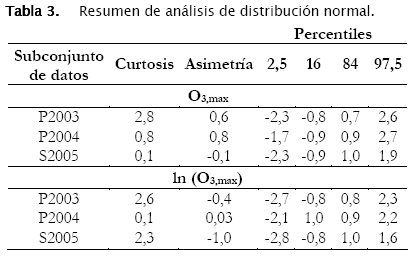
Los resultados para los subconjuntos de datos P2004 y S2005 son muy similares. Las variaciones se dan en términos del grado de ajuste de la distribución normal en especial sobre el coeficiente de asimetría y la curtosis. En los subconjuntos P2003 y P2004 la transformación logarítmica permite un mejor ajuste a la distribución dado que los coeficientes de curtosis y asimetría disminuyen y los límites para los percentiles se aproximan más a los teóricos, en especial para P2004. En la Tabla 3 se resumen estos resultados, encontrándose además que para S2005, la mejor distribución normal se presenta sin la transformación logarítmica indicada.

3.2 Análisis de correlación

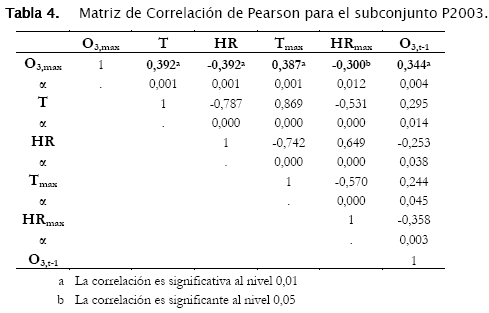
Para cada subconjunto de datos se aplica el cálculo de la Matriz de Correlación de Pearson tomando en cuenta las variables dependientes [O₃]_max y ln[O₃]_max. Se utilizan todas las variables predictoras obtenidas: temperatura (T), dirección del viento (WD), velocidad del viento (WS) y humedad relativa (HR) correspondientes al máximo diario de ozono; además de la temperatura máxima diaria (T_max), la humedad máxima diaria (HR_max), la velocidad del viento máxima diaria (WS_max) y las concentraciones máximas diarias del día anterior para el ozono [O₃]_{max, t-1} y la temperatura (T_{max, t-1}). En cuanto a la radiación solar, además de contarse con una gran pérdida de datos (Tabla 1) y a pesar de su inherente significado físico, se ha reportado una alta correlación lineal entre esta variable y la temperatura ambiente, considerándose que la segunda actúa como un sustituto natural de la primera [11].

La Tabla 4 muestra sólo las correlaciones estadísticamente significativas con un nivel de significancia α de hasta 0,05 para el subconjunto [O₃]_max P2003. Sobre estas variables predictoras se aplica el procedimiento de regresión en base a las ecuaciones (2), (4) y (5). El modelo descrito por la ecuación (6) no puede ser correlacionado dado que la variable T_{max, t-1} no ofrece una correlación lineal significativa en este caso.

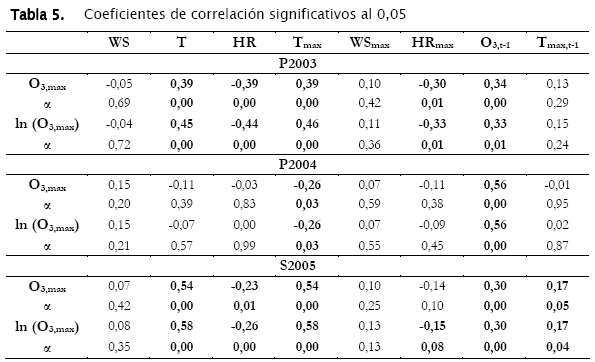
Un resumen de las correlaciones obtenidas se muestra en la Tabla 5. Notese que las variables de interés para la correlación varían de acuerdo al grupo de datos lo que justifica el hecho de que los modelos tengan no sólo coeficientes diferentes sino también variables predictoras diferentes.

El subconjunto de datos P2004 muestra sólo dos variables predictoras con correlación lineal significativa. En todos los casos, la correlación de la variable ln[O₃]_max es ligeramente mejor que la de O_3,max. El único subconjunto de datos que podrá generar un modelo mediante la ecuación (6) será el S2005 dado que tiene una correlación significativa para T_max,t-1. Para P2004, solo se podrá realizar el procedimiento de regresión con las ecuaciones (1) y (2). En general, se puede decir que los valores de regresión son bajos salvo T y T_max para S2005 (0,58 ambos) y O_3,t-1 (0,56) para P2004.

Desde el punto de vista práctico de un sistema de pronóstico, las variables T y HR, aunque correlacionadas en P2003 y S2005, no ofrecen la facilidad de su predicción comparadas con los valores máximos diarios de T, WS y HR.

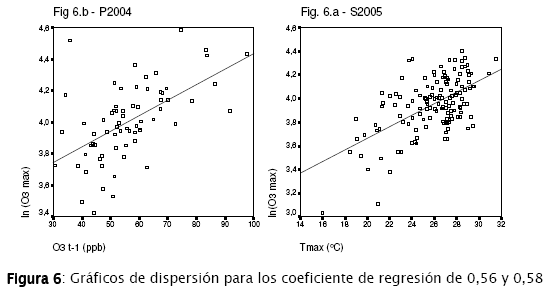
Las Figuras 6.a y 6.b muestran la relación gráfica de las correlaciones más altas encontradas mediante dos gráficos de dispersión junto con las líneas de regresión sobrepuestas.

Una vez reconocidas las principales variables predictoras, el sistema de regresión escalonada (stepwise) se encarga de seleccionar aquellas combinaciones más significativas.

3.3 Modelos de pronóstico

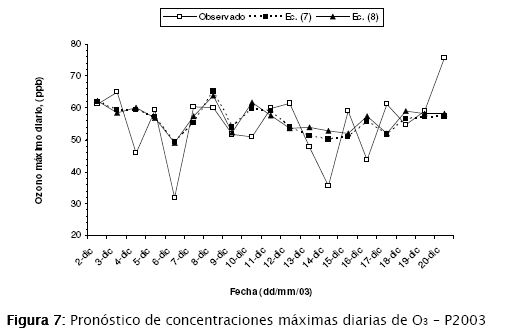
Para el subconjunto de datos P2003, el análisis de regresión proporciona los siguientes modelos,

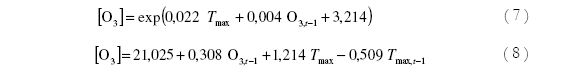
Comparados frente a los datos de validación separados para este subconjunto (Tabla 2), muestran el comportamiento de la Figura 7.

Los coeficientes de determinación R² para las ecuaciones (7) y (8) son de 0,267 y 0,239 respectivamente. Esto indica, por ejemplo para el primer valor, que todas la variables incluidas en el modelo pueden explicar el 26,7 % de las variaciones en la variable respuesta, mientras que el 73,3 % restante representa la variación de los residuos.

Puede verse en la Figura 7 que el modelo realiza una predicción por defecto en el caso de los valores extremos altos o bajos. Esta característica es propia de los modelos de regresión lineal desarrollados [16].

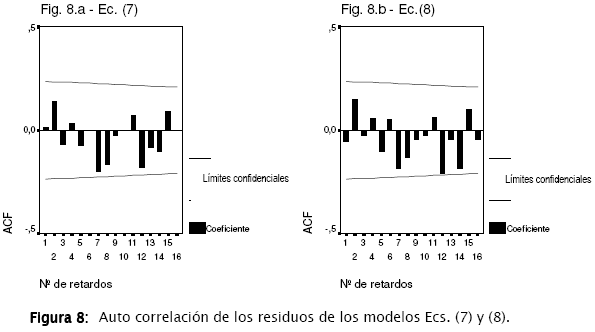
A fin de verificar la hipótesis de la independencia de los residuos, se muestra en la Figura 8 un análisis de auto correlación de los mismos para los dos modelos anteriores.

Ningún nivel de retardo (hasta 16) presenta un coeficiente de auto correlación (ACF) mayor al de los límites establecidos como dos veces el error estándar. Esto valida estadísticamente la hipótesis inicial sobre la independencia de los residuos. Se debe mencionar que, a través de pruebas estadísticas, se han encontrado problemas de colinealidad [7] en los dos modelos descritos por (7) y (8) y que posiblemente esta sea la causa de la pobre correlación mostrada en la Figura 7.

El análisis de regresión para el subconjunto de datos P2004 permite obtener el modelo de pronóstico:

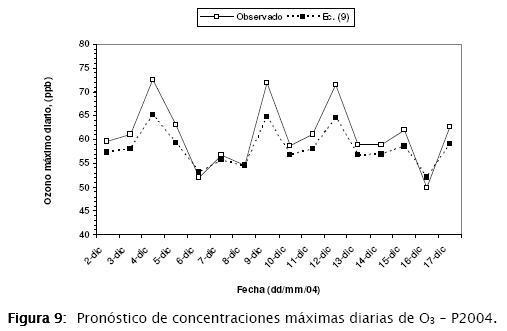
Si se analiza la Tabla 5 para P2004, se verifica que las variables predictoras estadísticamente significativas son T_max y O_3,t-1. Sin embargo, el proceso de regresión escalonado, indica que la variable T_max deja de ser significativa para el modelo el momento en que se añade la variable O_3,t-1 y es por eso que en la ecuación (9) solamente aparece la última variable mencionada. A continuación se muestra el gráfico de pronóstico obtenido.

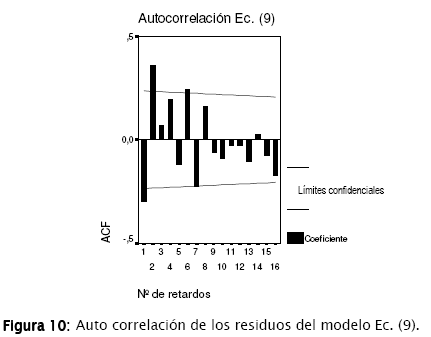
Para la ecuación (9), el coeficiente de determinación R² es de 0,314. Se ha probado adicionalmente un modelo conforme la ecuación (8), obteniéndose un R² de 0,370, que sin embargo, presenta elevados problemas de colinealidad en sus variables. En la Figura 10, el análisis de auto correlación muestra para este caso una violación a la hipótesis de la independencia de los residuos.

Lo anterior indica que debería generarse un mejor tipo de modelo para este caso. El modelo alternativo se denomina de error autocorrelacionado (AR) y su desarrollo está fuera del alcance de este artículo [5]. Sin embargo, según la Figura 9, el pronóstico en general presenta un mejor comportamiento que el obtenido para el subconjunto de datos P2003. Obsérvese también el mismo problema relacionado a la predicción por defecto para los valores más altos.

Finalmente, en el caso del subconjunto S2005, el modelo obtenido resulta en la siguiente relación,

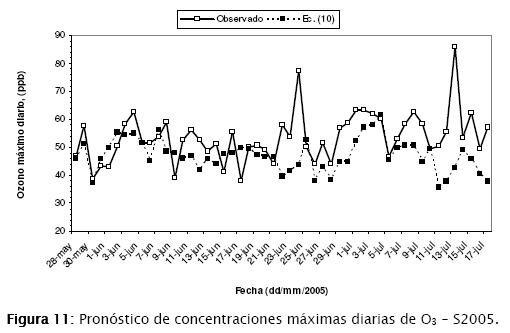
Como puede verse, este modelo ajusta la humedad relativa diaria máxima, lo cual confirma los resultados de correlación obtenidos en la Tabla 5. Sin embargo, el procedimiento de regresión escalonado retira la variable T_max aunque esta tenga un valor de correlación lineal significativo. La Figura 11 presenta la relación de pronóstico.

Para este caso, la cantidad de datos utilizada para la generación del modelo es mucho mayor que los anteriores subconjuntos (201 frente a 90). El coeficiente de determinación R² es de 0,408, un valor mucho más significativo que los anteriores casos. Al analizar la Figura 11 se puede apreciar sin embargo un conjunto de valores no pronosticados, en especial para el rango del 21,06 en adelante.

Al igual que para los residuos del modelo de la ecuación (9), el análisis estadístico de la ecuación (10) presenta una violación de la independencia de los residuos, indicando la necesidad de generar un modelo alternativo de error autocorrelacionado (AR).

3.4 Estadística de comparación

Wilmott [13] ha presentado un conjunto de estadísticos que han sido adoptados comunmente para la comparación del rendimiento de modelos de pronóstico. Dos mediciones muy utilizadas son el error medio absoluto (MAE en inglés) y la raíz del error cuadrático medio (RMSE) las cuales resumen las diferencias entre los valores observados y los pronosticados. El último estadístico puede ser descompuesto en el RMSE sistemático (RMSEs), el cual evalúa el rendimiento del modelo y de las variables predictoras incluidas y el RMSE asistemático (RMSEα) que se debe a los residuos y que no puede ser controlado. Un buen modelo se considera que tiene un RMSEα mucho mayor al RMSEs.

Un parámetro de comparación más útil es descrito por el índice de ajuste o "index of agreement" (IA), el cual se define como:

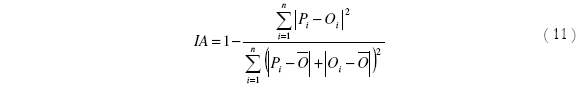
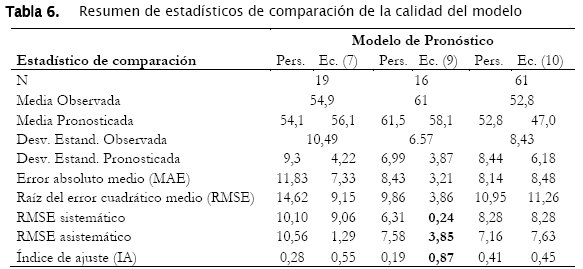
Donde P_i y O_i son las concentraciones pronosticadas y observadas respectivamente. El IA varía entre 0 y 1 donde el 0 representa la peor situación de ajuste. La Tabla 6 presenta un resumen de los estadísticos de comparación aplicados a los modelos estudiados.

En la Tabla 6 es evidente que el modelo de la Ec (9) presenta los mejores parámetros de ajuste en cuanto al IA (0,87) y la diferencia entre RMSEs < RMSEα. En todos los casos, los modelos planteados resultan en un mejor Indice de Ajuste que los modelos de persistencia.

Por lo visto, el uso de una mayor cantidad de datos para la generación del modelo de la ecuación (10) no ha contribuido en lograr un modelo de mayor alcance para los tiempos de predicción.

 

4    Conclusiones

Inicialmente, se debe comentar que una importante proporción del tiempo empleado en obtener los resultados descritos en este documento se ha empleado en el tratamiento de los datos. Una conclusión inmediata sobre este punto resulta en la necesidad de establecer un protocolo de almacenamiento de datos para las estaciones de la red de monitoreo automático, independientemente de las variables que se manejen. El enfoque ideal será tener a disposición de cualquier investigador, una base de datos histórica que sea permanentemente alimentada. De este modo, los esfuerzos podrán ser mejor enfocados hacia el desarrollo de mejores y más confiables modelos.

El análisis de estacionalidad descrito, se ha basado en un enfoque puramente aritmético y gráfico. Debe analizarse la posibilidad de mejorar el procedimiento de homogenización de grupos de datos utilizando técnicas de análisis de conglomerados u otras herramientas estadísticas que garanticen una mejor agrupación de los mismos. Sin embargo, como una primera aproximación, la estacionalidad ha sido verificada.

Con referencia a trabajos revisados, el caso de la estación de SEMAPA fue el único que contaba con la medición de variables meteorológicas en el mismo sitio, el grado de correlación encontrado frente a las concentraciones máximas diarias de ozono es bajo. En dos casos [9][11], las estaciones meteorológicas se encontraban en sitios distantes de las estaciones de medición de la calidad del aire y aún así, los valores de correlación reportados son más altos que los del presente caso. Es posible que la restricción en la cantidad de datos utilizados no permita mejorar esta correlación.

Aunque no se detalló el análisis de colinealidad [7] realizado para los modelos obtenidos, en la mayoría de ellos se encontraron variables que presentaban una alta colinealidad. Este puede ser un factor adicional que afecta al grado de rendimiento de los pronósticos obtenidos.

Como conclusión final, podemos indicar que se hace necesario el desarrollo de modelos que tomen en cuenta la auto correlación del error, dado que la hipótesis básica de la dependencia de los residuos fue violada en dos de los tres modelos.

 

Referencias

[1] Bascopé D., La Red de Monitoreo de la Calidad del Aire de Cochabamba. Acta Nova-Revista de Ciencias y Tecnología. Universidad Católica San Pablo. Vol.1, N°3, 282-291, Cochabamba, Bolivia. Julio/Diciembre 2001

[2] Bascopé D., Resultados del monitoreo atmosférico en la ciudad de Cochabamba. Acta Nova-Revista de Ciencias y Tecnología. Universidad Católica San Pablo. Vol.2, N°1, pp.116-129, Cochabamba, Bolivia, Diciembre 2002.

[3] D.M. Holland y T. Fitz-Simons. Fitting statistical distributions to air quality data by maximum likelihood method. Atmospheric Environment Vol. 16, No. 5, pp. 1017-1076, 1982.

[4] D.S. Miller et al. Ozone forecasting tool development to support forecasting for the EPA AIRNow Program. Sonoma Technology Inc. Technical Report, 2002.

[5] Damon J., Guillas S., The inclusion of exogenous variables in functional autoregressive ozone forecasting. Institut de Statistique d l´Université de Paris. Rapport Technique N°4, 2001.

[6] EPA, Guidelines for Developing an Air Quality (Ozone and PM_2.5) Forecasting Program. EPA-456/R-03-002. Junio 2003.

[7] Ferrán A. Magdalena, SPSS para Windows. Análisis Estadístico. Ed. McGraw-Hill. México, 2001.

[8] G. McCollister. Linear Stochastic Models for forecasting daily maxima and hourly concentrations of air pollutions.. Atmospheric Environment Vol. 9, pp. 417-423, 1975.

[9] Jorquera H. et. al. Forecasting ozone daily maximum levels at Santiago, Chile. Atmospheric Environment Vol. 32, No. 20, pp. 3415-3424, 1998.

[10] La Tran B., Regression modelling of air pollution from highway vehicle. Master Thesis, Hanoi University of Technology. Septiembre 2002

[11] M. Hubbard y W.G. Cobourn. Development of a regression model to forecast ground-level ozone concentration in Louisville, KY.. Atmospheric Environment Vol. 32, No. 14/15, pp. 2637-2647, 1998.

[12] Milton J.S., Arnold J.C., Probabilidad y Estadística. Ed. McGraw-Hill. México, 2004.

[13] S.M. Robeson y D.G. Steyn. Evaluation and comparison of statistical forecast models for daily maximum ozone concentrations. Atmospheric Environment Vol. 24B, No. 2, pp. 303-312, 1990.

[14] Seinfeld J.H., Pandis S.N. , Atmospheric chemistry and physics: From air pollution to climate change. Ed. Wiley-Interscience. USA, 1998.

[15] Th. Slini, K. Karatzas y A. Papadopoulos. Regression analysis and urban air quality forecasting: an application for the city of Athens . Global Nest: the Int. J. Vol 4, No 2-3, pp 153-182. 2002

[16] Thompson M. et al., A review of statistical methods for the meteorological adjustment of trophospheric ozone. National Research Center for Statistics and the Environment, University of Washington. Technical Report Series, 1999.