Apunte

 

Teoría general para flexión y corte (régimen elástico)

 

 

Héctor Claiman, Cristian Reppeto

 

 

---

 

 

(Simplificación del método propuesto por Gere-Timoshenko)

En los capítulos 9.4 y 9.8 del libro Mecánica de los Materiales de los autores (ver apéndice en jpg) citados se aborda el problema general de la flexión y corte para el caso en que los ejes y y z no sean Principales de Inercia y por razones prácticas no se desea determinar los mismos y descomponer la flexión oblicua en dos flexiones normales como es habitual.

Este es el caso para secciones abiertas (simples o compuestas) formadas, por ejemplo, por perfiles donde no se disponen de los momentos de inercia principales y sí se cuenta (o es más fácil calcularlos) con momentos de inercia respecto a ejes ortogonales no principales. Un ejemplo de ello son las secciones que se muestran en las figuras 9.13 y 9.15 del libro de Timoshenko.

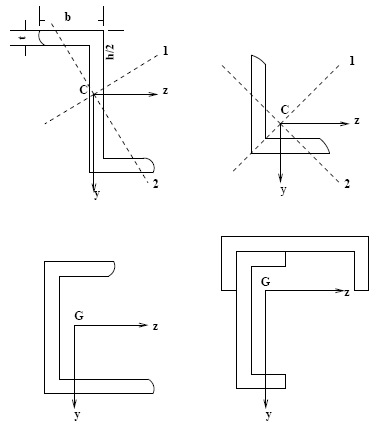
Siguiendo a Timoshenko y respetando la convención por él adoptada, para una sección cualquiera sometida a flexión:

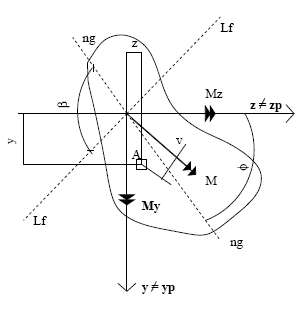
Resulta según Timoshenko:

Fórmula de difícil memorización, donde el eje neutro tiene por ecuación:

más fácil en cambio es de recordar la expresión general (Fliess-11.153)

(β menor ángulo entre Lf y n_g-n_g) y aprovechar esta expresión que formalmente es idéntica a la ecuación 2 para determinar en forma práctica las tensiones τ y σ para los casos planteados donde la misma sea de mayor utilidad.

En efecto, para un par de ejes conjugados n y v cualesquiera siempre es posible determinar matemáticamente el ángulo que forman entre ellos (Lf y n_g-n_g son conjugados de inercia en el baricentro y para la figura dada):

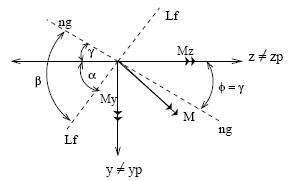
En Fliess, 2do curso, figura 11.22. Los ejes z e y no son ejes principales.

Donde

Desarrollando se puede llegar a demostrar la igualdad de las expresiones 1 y 11.153. A nosotros nos interesa M no según z e y sino asumir que z es un eje neutro n-n e y es eje neutro z-z en cuyo caso existen dos líneas de fuerzas, conjugadas respectivamente de ellas:

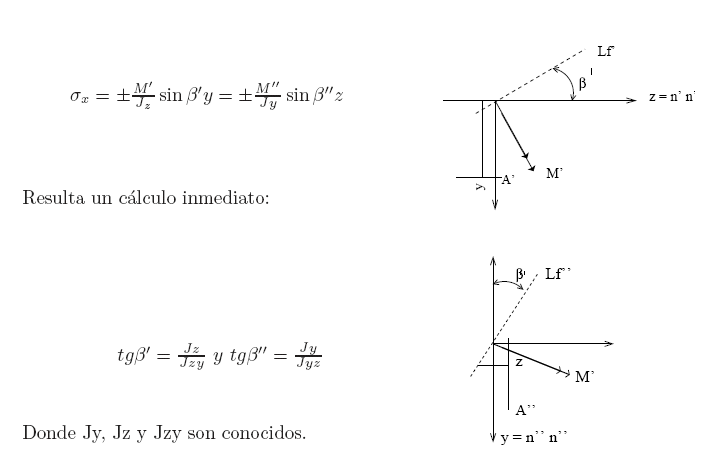
En efecto, lo único que hemos hecho es aplicar la fórmula de la flexión oblicua descomponiendo la flexión también en coordenadas oblicuas para aprovechar el conocimiento de Jy, Jz y Jzy de cálculo rápido en los casos que nos interesa.

 

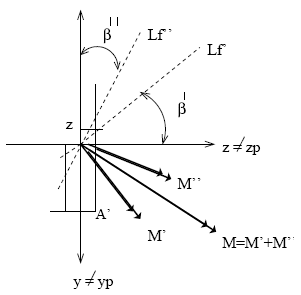
De donde se pueden encontrar M' y M" ya que todos los datos son conocidos. Las direcciones de M' y M" o de sus respectivas líneas de fuerzas son también las coordenadas oblicuas del problema.

Esto resulta de utilidad no tanto en flexión sino cuando quiere determinarse tensiones de corte en perfiles donde se conoce por la propiedad de los mismos (espesor delgado y distribución constante en el ancho) que la τ_xresultante resulta tangente a la línea media del perfil, no conociéndose su valor, pero conociéndose Jy, Jz y Jzy siendo z e y no principales.

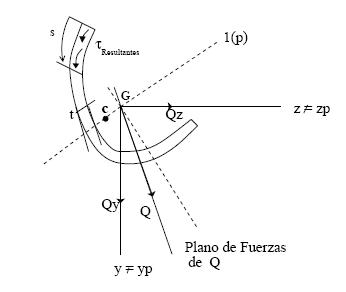
El plano de corte puede no coincidir con la línea de fuerza (intersección del plano de momentos con la sección). En lugar de descomponer según 1 y 2 (z_p e y_p) se puede en forma general (Timoshenko, 9.8):

(Suma algebraica porque se conocen las direcciones y todas son coincidentes).

Este procedimiento permite también, conocida la ley de distribución de las τ_xresultante determinar la posición del centro de corte, C, planteando la equivalencia de los momentos de las fuerzas Qy y Qz, respectivamente en los momentos según x de las fuerzas interiores de Corte que nos dan la abcisa y la ordenada de C. Sin embargo, son de difícil memorización y se debe ser cuidadoso con los signos, por lo que también es útil el procedimiento anterior para determinar la posición del centro de corte y las tensiones τ_r resultantes, plantearnos para Qy solamente: (para Qz similarmente).

Se debe tener presente siempre, y para cualquiera de los procedimientos a utilizar, que las fórmulas nacen de suponer dM/dx = Q, sólo participan entonces aquellos M variables con x. Las fuerzas de resbalamiento son las originadas por ellos. Por ejemplo, si existieran pares constantes en una dirección y flexión variable en otra, la línea de fuerza (que resulta de componer todos los momentos) no coincide con la traza del plano de corte que es la que se utiliza).

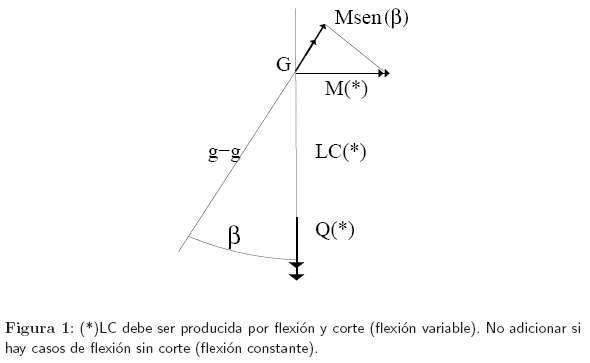
Ejemplo:

En forma genérica

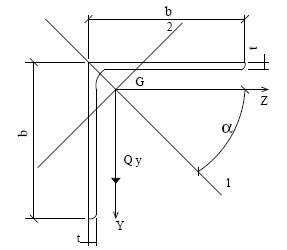
Si se da Q=Qy, Jy, Jz y Jzy, Calcular

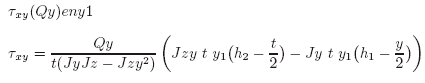
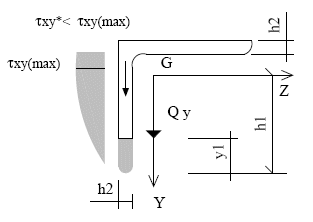
fórmula general (muy engorrosa)

Otra forma: Clásica

Q_y = Q₁+ Q₂

 

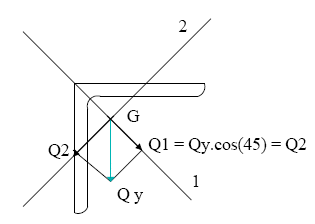
Los Q_h se anulan (Q'_h + Q''_h), los Q_v se suman Q_y = Q'_v + Q''_v

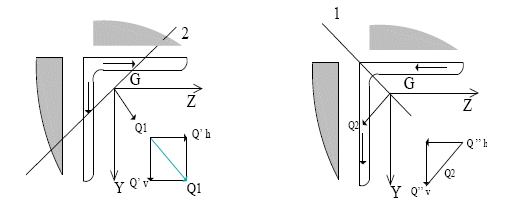
Otra forma: Propuesta del Ing. Héctor Claiman, para este ejemplo simple conviene el método clásico

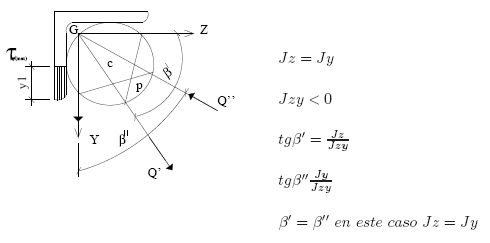
Sólo para τ_xy por sencillez, pero válido para cualquier τ.

 

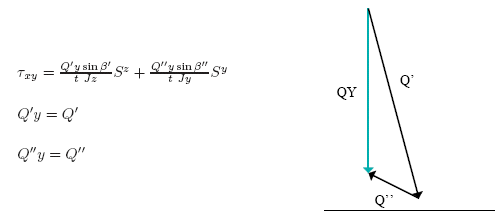
El mismo ejemplo:

En forma numérica. Determinación de τ_xy-max para el perfil de la figura, Angulo 100-100-10

Fórmula General, τ_xy-máx:

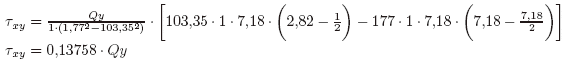
Por descomposición de Qy en Q1 y Q2, τ_xymáx:

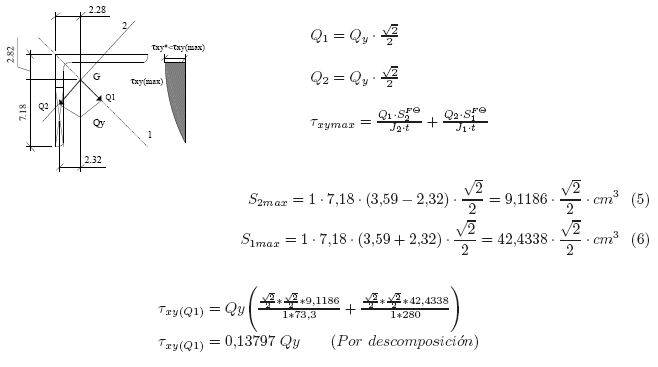
Por el método simplificado de suponer que trabaja el alma solamente, τ_xymedia:

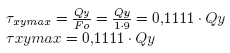
Vemos que la aproximación da un error >20% con τ_xy en defecto.

Por descomposición según Q' y Q" (Respectivos conjugados de z e y), τ_xymáx:

 

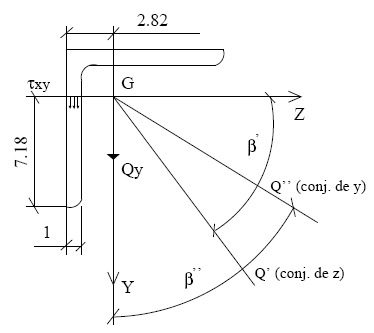
Resumen (la unidad de τ = [Q]/cm²)

Ejemplo:

Con el método propuesto para perfiles compuestos. (Genérico)

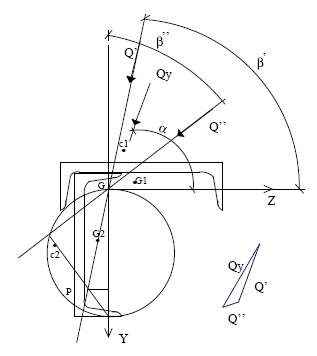
Coordenadas Oblicuas.

Q" dirección conjugada de y

Q' dirección conjugada de z

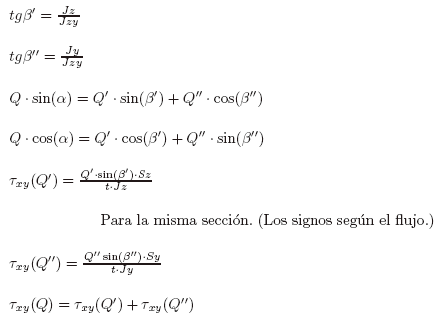
Caso Particular: Q = Qy se resuelve (similar).

g-g conjugada de "y"

β ángulo entre g-g e "y"

c₁ y c₂ centro de corte de los perfiles simples (son datos o se calculan previamente)

Comentario:

Existe otra fórmula general más complicada

o bien τ_xy(Qy) = t_xy(Q2) simplificando ya que se conoce Q₂ en C₂.

 

Ejemplo Genérico:

Determinar la posición del centro de corte según z (de la misma forma que según y). Ver la sencillez del método. Mediante la descomposición de Q_total en Q_parciales para cada perfil proporcional a sus rigideces flexionales respecto del eje z(eje de referencia respecto del que se calcula la coordenada del centro de corte total, ver pág 10).

No interesa la dirección ni el valor de Q para el centro de corte, si, como se reparte entre perfiles, es un concepto geométrico independiente de las solicitaciones. Depende de la distribución interna, relación entre las partes, de las tensiones tangenciales.

Ejemplo: Determinar la posición de Q_y (la abcisa según Z solamente) para que no haya torsiones en la sección compuesta.

Suponemos 2 UPN 200.

Aquí es muy fácil el cálculo de los momentos de inercia respecto de z e y.

F₁ = F₂ = 32,2cm⁴

J_zG2 = J_yG1 = 1910.cm⁴

J_zG1 = J_yG2 = 148.cm⁴

Posición de G:

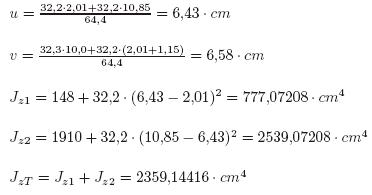
Posición de e₂:

Otra forma(Timoshenko)

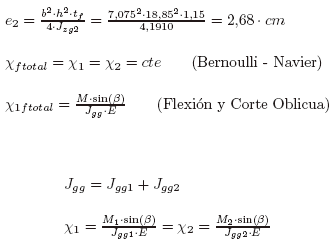
J_gg: Momento de inercia respecto de g1 — g1 (conjugados de LC₁) de la sección 1.

Luego como M = M₁ + M₂, M₁ = (J_gg1/J_ggT) * M y M₂ = (J_gg2/J_ggT) * M, distribución de M según rigideces a flexión de los perfiles.

Posición de s: (por donde debe pasar Q_y respecto de G). Ver Timoshenko 9.5 - pág 521.

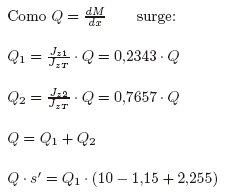
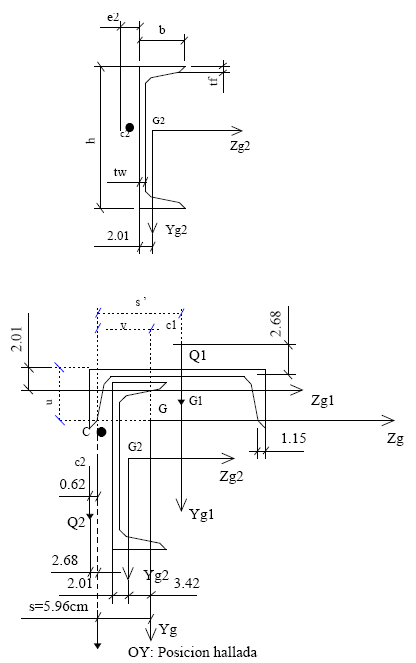
s' = 9,378cm, desde G₁, o sea, s = 5,96cm desde G. Similarmente respecto de "y” nos daría la otra coordenada del centro de corte del perfil compuesto.