Artículo Científico

 

Minimización de funcionales en Espacios de Banach Reflexivos

 

 

Edson Arrázola Iriarte

UNINCOR, Minas Gerais - Brasil
e-mail: eaai86@ig.com.br

 

 

---

 

 

1. Introducción

El clásico Teorema de existencia de Weierstrass nos dice que el problema de minimización

tiene solución, si el funcional Φ : A ⊂ X → es continuo en un subconjunto compacto A de un espacio de Banach X de dimensión finita. Por ejemplo, si A = [a, b] es un intervalo cerrado, la función Φ tiene un mínimo, mas aún, Φ es una función acotada. Entretanto, no es inmediato que funciones continuas en toda la recta tengan esta propiedad. La función Φ(u) = — u² + 1 tiene mínimo en el intervalo [—1,1], pero no está acotada inferiormente ni alcanza su mínimo en . Vemos entonces que no basta la continuidad del funcional Φ para que el problema de minimización

tenga solución. Necesitamos de una condición adicional que esté relacionada con el comportamiento de la función fuera de un subconjunto compacto de X. En efecto, si Φ : → es una función continua restricta a un intervalo cerrado I, tiene mínimo en I. Si Φ se hace suficientemente grande fuera de I, este mínimo también será un mínimo en (mínimo absoluto). Mas precisamente, se tiene el

Teorema 1.1 Si Φ : → es una función continua tal que

entonces, Φ alcanza su mínimo en .

Análogamente, si X = ^N y Φ es una función continua que se hace suficientemente grande fuera de una bola cerrada, el problema (1) tiene solución, ver Teorema 2.1.

Desafortunadamente, el Teorema de Weierstrass no es útil cuando se trata de espacios de Banach de dimensión infinita, puesto que, "bolas cerradas en estos espacios no son compactas". Esta dificultad se resuelve usando el Teorema de Eberlein-Šmulian. Teorema 3.1, que nos garantiza que una sucesión acotada en un espacio de Banach reflexivo, posee una subsucesión débilmente convergente.

En estas notas discutimos las condiciones sobre el funcional Φ que nos garantizan la existencia de solución para el problema de minimización (1). En la primera parte estudiamos el caso X = ^N . En la segunda parte, estudiamos el caso de los espacios de Banach de dimensión infinita. Suponemos que el lector está familiarizado con los conceptos básicos de Análisis Funcional, sin embargo, muchos de los conceptos aquí utilizados y sus consecuencias son introducidos en el momento en que se hacen necesarios. Para más detalles, sugerimos consultar el libro de Brezis [4] o el de Kreyszig [2], que son excelentes referencias sobre el asunto.

Finalmente, observemos que si u₀ ∈ X es solución de (1), y el funcional Φ : X → es Frechét diferenciable, u₀ será un punto crítico de Φ, o sea,

que corresponde a la clásica ecuación de Euler-Lagrange. Además, si Φ es estrictamente convexo, u₀ será único. Estos tópicos serán discutidos en una segunda parte de este trabajo. Al lector interesado sugerimos consultar [1].

 

2. Minimización en ^N

La demostración del siguiente Lema puede encontrarse en [3].

Lema 2.1 (Weierstrass) Sean (A, d) un espacio métrico compacto y Φ : A → una función continua. Entonces Φ alcanza su mínimo en A, o sea, existe u₀ ∈ A tal que

Teorema 2.1 Sea Φ : ^N → una función

(i) continua

y (ii) coerciva , o sea,

Entonces Φ alcanza su mínimo en ^N .

Demostración: Como Φ es coerciva, existe R > 0 tal que para |u|> R

La bola cerrada B_R = {u ∈ ^N : |u| ≤ R} es compacta, entonces por el Teorema de Weierstrass, existe u₀ ∈ B_R tal que Φ(u₀) ≤ Φ(u), ∀u ∈ B_R. Por otro lado, si u B_R se tiene que Φ(u) > Φ(u₀). Por consiguiente

Observación 2.1 Este resultado nos garantiza la existencia del mínimo, pero no nos dice nada sobre la unicidad, ver por ejemplo la función Φ : → definida por Φ(u) = u² si u ≠ 0 , Φ(0) = 0. Esta función es continua en y es tal que Φ(u) ≥ 0 para todo u ∈ . Luego, u = 0 es un mínimo de Φ. Es claro que en cualquier vecindad de 0 existen puntos u ≠ 0 tales que Φ(u) = 0.

 

3. Minimización en espacios de dimensión infinita

En lo que sigue, si X es un espacio de Banach, designaremos por X' = L(X, ) el dual topológico de X, o sea, el espacio de los funcionales lineales y continuos sobre X. El espacio X' está dotado de la norma

El dual de X' se denota por X", y es conocido como bidual de X. El dual de X' está dotado de la norma

Definamos la inyección canónica J : X —> X" como sigue: sea u ∈ X fijo, la aplicación φ → φ(u) de X' en es lineal y continua sobre X'. Asi pues,

Claramente J es lineal y una isometría, o sea, ||Ju||_x" = ||u||_X. Decimos que X es reflexivo si J(X) = X". Cuando X es reflexivo se identifican X y X". Observemos que todo espacio de Hilbert H es reflexivo, ver [2].

3.1. Convergencia débil

3.1  For the development of Functional Analysis, the most important concepts introduced by Hilbert (1906) were what he calls "continuity" and "complete continuity", which correspond to what will later be called the "strong " and "weak" topologies on Hilbert space. (Jean Dieudonné - 1981)

3.2  (Riesz - 1918) Un espacio de Banach es de dimensión finita si y solamente si la bola cerrada unitaria es compacta.

Este famoso resultado nos dice que en espacios de Banach de dimensión infinita existen sucesiones acotadas (u_n) que no poseen subsucesiones convergentes. Esta pérdida de compacidad en espacios de Banach de dimensión infinita, es responsable por algunas dificultades que se encuentran en el cálculo de variaciones y en la teoría de las ecuaciones diferenciales parciales. Para resolver estas dificultades, en 1906, Hilbert introdujo el concepto de convergencia débil.

Definición 3.1 (Convergencia débil) Sea X un espacio de Banach. Una sucesión (u_n) converge débilmente a u ∈ X, escribimos u_n → u, si

Recordemos que una sucesión (u_n) en X converge fuertemente, o converge en norma, si ||u_n - u|| → 0.

Observación 3.1 Cualquier sucesión fuertemente convergente es débilmente convergente, sin embargo la recíproca es falsa. En el caso de espacios de Banach de dimensión finita, los dos conceptos coinciden, ver [2].

Observación 3.2 Una sucesión (u_n) débilmente convergente, u_n → u, es acotada. Más aún

La demostración de esta afirmación puede encontrarse en [4] o en [2].

Si H es un espacio de Hilbert, el Teorema de representación de Riesz nos garantiza que si φ ∈ H', existe un único v ∈ H que lo representa, o sea, existe un único v ∈ H tal que

Entonces, u_n → u si y solamente si (v,u_n) → (v,u) ui para todo v ∈ X.

Ejemplo 3.1 Consideremos el siguiente espacio de Hilbert

con el producto interno definido por

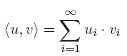
La sucesión e_n = (0,... , 0, 1, 0,...) es tal que e_n → 0 = (0, 0, ...). En efecto se tiene que

La demostración del siguiente Teorema puede encontrarse en Yosida [5].

Teorema 3.1 (Eberlein - Šmulian) Un espacio de Banach X es reflexivo si y solamente si toda sucesión acotada (u_n) posee una subsucesión (u_nj) débilmente convergente. Por lo tanto, bolas cerradas en X son débilmente compactas.

3.2. Semicontinuidad inferior

Decimos que el funcional Φ : X → es débilmente continuo si para una sucesión (u_n) tal que u_n → u se tiene que Φ(u) = lím Φ(u_n)

Ya vimos que en espacios de dimensión finita, el problema de minimización (1) tiene solución si Φ es un funcional continuo y coercivo. Parece natural que en el caso de los espacios de dimensión infinita, si "debilitamos" la continuidad del funcional garantizamos la existencia de solución para el problema (1), sin embargo, esta condición es incompatible con la coercividad como veremos en el siguiente ejemplo.

Ejemplo 3.2 Supongamos que Φ : l₂ → es un funcional

(i) débilmente continuo, y

(ii) coercivo

La sucesión (e_n) es tal que e_n → 0 y ||e_n|| = 1 . Sea r > 0 arbitrario, entonces r e_n → 0 y ||re_n|| = r . Como Φ es débilmente continuo se tiene que

lo que contradice la coercividad de Φ.

Observemos que si en (2) tuviésemos que Φ(u) ≤ lím Φ(u_n), la incompatibilidad desaparece, esta condición es conocida como semicontinuidad inferior.

Definición 3.2 Decimos que el funcional Φ : X → es semicontinuo inferior si para cualquier sucesión (u_n) ⊂ X tal que u_n → u se tiene que

Si esta desigualdad es válida para toda sucesión (u_n) ⊂ X tal que u_n → u, decimos que el funcional Φ es débilmente semicontinuo inferior.

Observación 3.3 Es claro que si Φ es débilmente semincontinuo inferior es semicontinuo inferior, pues cualquier sucesión fuertemente convergente es débilmente convergente.

Ejemplo 3.3 La función Φ : → definida por

es semicontinua inferior, si y solamente si c ≤ 0.

Ejemplo 3.4 La función Φ : → definida por

es semicontinua inferior. Entretanto, si Φ(u) = u + 1 para u ≥ 0, y Φ(u) = —u para u < 0, Φ no es semicontinua inferior.

Ejemplo 3.5 Sea Φ : [a, b] → una función continua. Entonces Φ es débilmente semicontinua inferior. En efecto, los conceptos de convergencia fuerte y débil coinciden, luego

Teorema 3.2 Sea X un espacio de Banach reflexivo y sea Φ : X → un funcional

(i) débilmente semicontinuo inferior y

(ii) coercivo, o sea,

Entonces Φ es acotado inferiormente y alcanza su mínimo en X

Demostración: Como Φ es coercivo existe R > 0 tal que para ||u|| > R

Sea

donde B_R = {u ∈ X : ||u|| ≤ R}. Entonces, existe (u_n) ⊂ B_R tal que Φ(u_n) → ρ. Como (u_n) es una sucesión acotada y X es reflexivo, por el Teorema de Eberlein-Šmulian, posee una subsucesión (u_nj) tal que u_nj → u₀ . Es claro que

Usando la observación 3.2 concluimos que u₀ ∈ B_R, entonces Φ(u₀) ≥ ρ. Finalmente, como Φ es débilmente semicontinuo inferior se tiene que

de ahí el resultado                                                                                           

Observación 3.4 Otra demostración de este teorema puede encontrarse en [1].

 

Referencias

[1] Dragiša Mitrović y Derko Zubrinić, Fundamentals of Applied Functional Analysis, Addison Wesley Logman, 1998.

[2] Erwin Kreyszig, Introductory Functional Analysis and Applications, John Wiley and Sons Inc., 1978.        [ Links ]

[3] Elon Lages Lima, Espagos Métricos, Projeto Euclides, IMPA, Rio de Janeiro, 1977.        [ Links ]

[4] Haïm Brézis, Análisis Funcional, Alianza Editorial, 1984.         [ Links ]

[5] K. Yosida, Functional Analysis, Springer, 1965.        [ Links ]