Historia de las Ciencias

 

¿Qué es lo que Dios hizo? Escueta historia de los números desde Adán hasta hoy

(1ra Parte)

 

 

Oscar Pino O.

Sociedad Boliviana de las Ciencias
e-mail: opinoo@latinmail.com

 

 

---

Resumen

Contamos la manera en que Dios se las arregló con el hombre para hacerle creer que tuvo participación en la sabia construcción del universo, logrando así levantarle la autoestima e inducirle a comprender la obra de su divina creación. Esto, en cuanto a los números se refiere.

---

 

 

"Dios hizo los números enteros, el resto es obra del hombre"

Leopold Kronecker

 

La concepción

"Dios algunas veces geometriza"

Platón

Al parecer hemos aceptado, final y humildemente, que hace 4,4 millones de años éramos unos simples animalejos, desgarbados, ceñudos, encorvados, pequeños, temerosos, hambrientos, pobladores de ramas, presas frecuentes y carnívoros ocasionales. Como australopithecus amanensis¹ no conocíamos el lenguaje y nos comunicábamos por chillidos disparejos que bastaban para el único objetivo que por entonces ocupaba todo nuestro interés: sobrevivir. Poco tiempo después (unos 100.000 años) pasamos a ser australopithecus afarensis², tan velludos e indefensos como antes, pero de caminar más airoso pues nos equilibrábamos sobre nuestras patas posteriores, lo que dejaba nuestras manos libres para utilizarlas en la ocasión pertinente. Un tanto luego (unos 500.000 años) éramos australopithecus boisei³ y aunque todavía no habíamos encontrado muchas maneras de ocupar inteligentemente nuestras manos ya nos servían para dar de pedradas al enemigo. Finalmente, los pulgares opuestos se develaron muy útiles por lo que nos transformamos en el homo habilis⁴ (entre 2,3 y 1,5 millones de años) y nos dedicamos a deshojar unas ramitas finas para comer gusanos y a correr detrás de algún conejo provistos como estábamos de largos palos que habíamos delicadamente afilado con premeditación y alevosía. Seguidamente, (pasados unos 600.000 años) se nos soltó la lengua. Convertidos en el pithecantropus erectus⁵, aprovechamos el fuego y las largas noches de invierno para sentarnos a escuchar las noticias del día y a comentar la extinción de nuestro primo hermano el homo neanderthalensis⁶. Vaya uno a saber si eso pasó porque no supieron adaptarse al medio, o si no tuvieron la prudencia de aliarse con los perros, como lo hicimos nosotros, o si los empujamos un poquito a que se vayan porque sentíamos que el mundo era demasiado pequeño para ellos y nosotros. Lo cierto es que, por entonces, se nos ocurrió decir "una cabeza", "dos manos", "muchos pasos". Habíamos descubierto la singularidad, la dualidad y la pluralidad. Bastaba. No necesitábamos mayor precisión en nuestras cuentas. En efecto, Dios había instruido a los números para que sólo aparezcan cuando los necesitemos. Y en aquellos tiempos sólo necesitábamos tres números: uno, dos, muchos.

Cuentan que un señor feudal irritóse al ver que, en una de las torres de su castillo, se había instalado un oscuro e irreverente cuervo. El animal, en su intento de anidar, ensuciaba el lugar con insistencia. El castellano decidió eliminar al intruso por lo que subió armado y decidido a la torre. Al verlo, el cuervo se alejó yéndose a posar en un árbol cercano donde esperó que el castellano descendiese. Este pensó: "si subo con un amigo, lo verá bajar, regresará y acabaré con él". Pero el cuervo viendo que eran dos, no regresó hasta que los dos hubieron bajado. El castellano no se rindió y subió con dos amigos, pero sin éxito. El cuervo sabía que eran tres. Empecinado, el señor del castillo subió con tres amigos y fracasó. Pero cuando subió con cuatro (con él eran cinco personas) y aparentaron marcharse todos, el cuervo regresó y halló la muerte. Lamentablemente la inocente avecilla sólo sabía contar hasta cuatro.

Pero una vez que la ambición se instala se desenfrena, así que sobrepasamos pronto al cuervo que cuenta hasta cuatro (ver recuadro) y dejamos de ser sólo el homo habilis para ser el homo sapiens⁷. Contamos nuestros dedos, contamos nuestras cosas, nos contamos nosotros, y en un supremo acto de soberbia pasamos largas noches contando las estrellas. Entonces descubrimos que había una cantidad más grande que todas las que habíamos encontrado, la que daba razón de los astros del cielo y de los granos de arena en las playas del mar: el infinito.

Por fin teníamos un sistema completo: uno, dos, tres, cuatro,..., un millón, muchos, infinito.? Para qué serviría un número más grande que un millón? Nada parecía tener una cardinalidad más grande que un millón y si la tenía era "muchos" y si era aún mayor era "infinito".

Pero Dios le tenía preparada una zancadilla a nuestra angurria de conteo. Dejó que partamos el pan y dividamos la herencia. Así la unidad se quebró surgiendo, de sus retazos, las fracciones. Entonces dijimos "un medio", "un tercio", "un cuarto", "un quinto"... y las fracciones de numerador igual a uno aparecieron, prometiendo describir perfectamente todo pedazo de unidad bajo la forma de la suma de unas cuantas, bien escogidas, de entre ellas. Por ejemplo:

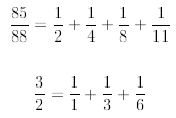
Quedan, como testimonio de ese momento de la historia de nuestro intelecto, muchas tablillas de arcilla y unos cuantos papiros. En efecto, una vez que nos asentamos sobre las fértiles tierras de entrerríos⁸, pasamos largos años estudiando el comportamiento de los números y su relación con la realidad. Aprendimos a medir. Inventamos la posesión de la tierra y nos la distribuimos. Calculamos longitudes, áreas y volúmenes. Construimos templos, edificios, puentes, caminos, ciudades y una herramienta nueva: la matemática. Más que el yunque y el martillo, mucho más que el azadón y la hoz, la matemática pretendía ser el instrumento ideal para comprender y dominar nuestro entorno, es decir nuestra realidad. Y sin embargo...

"Las proposiciones matemáticas, en cuanto tienen que ver con la, realidad, no son ciertas; y en cuanto son ciertas, no tienen nada que ver con la realidad"

Albert Einstein

No obstante, como Sumerios, dejamos una cierta herencia. Dividimos la tierra y el tiempo. Creamos las leyes. Asignamos nombres a las constelaciones y Gilgamesh⁹ se llevó la creación en un barco mientras llovía interminablemente. Los conceptos de infinito y eternidad echaron raíces en nuestro intelecto mientras que la idea de la inmortalidad nos embriagaba. Por entonces faltaban 3000 años para el advenimiento del Salvador.

Alrededor de Babilonia, comenzamos a abandonar los "un pan", "dos niños", "tres árboles" para decir "uno", "dos", "tres". El úmero se desprendía de la cosa. El número como número, por sí y sin referencia concreta, se hacía. El número nacía.

 

El nacimiento

"Dios algunas veces aritmetiza"

C. G. J. Jacobi

Hace cuarenta siglos, en el valle del Nilo, alguno de nosotros pensó: "Dejaré constancia de que la manera justa de repartir una hogaza de pan entre diez obreros, es la de dar un décimo a cada uno... y probaré que es cierto". Tomó un papiro y escribió:

"Cada obrero recibe de hogaza. Multiplica por 10. Hazlo de esta forma:

En efecto, como...

la solución es correcta.

Luego añadió, en el mismo documento, la manera de repartir con justicia, 2, 6, 7, 8 y 9 hogazas de pan entre 10 obreros y otros problemas muy interesantes, como el cálculo de áreas de triángulos, rectángulos, trapecios y círculos, pendientes, alturas, bases y volúmenes de pirámides y las progresiones aritmética y geométrica.

Dos siglos después, hacia el año 1650 antes de Cristo, Ahmes, escriba del Faraón, copió¹⁰ ese pergamino. Así quedó constancia del uso adecuado que dimos, en ese entonces, a los números naturales, a las fracciones positivas que tienen numerador 1 y a la fracción excepcional: .

En consecuencia, podemos decir que, grosso modo, los números llamados naturales (sin el cero) y las fracciones positivas de numerador uno (además de la fracción ) eran todo nuestro instrumental matemático (en cuanto a herramientas de cálculo se refiere); esto hace, más o menos, cuarenta siglos. Y pensamos que eran suficientes...

 

La infancia

Mucho después, hacia el siglo siete antes de Cristo, en Grecia, provistos de una escritura numérica deficiente pero hábiles en geometría, nos dimos a la tarea de comprender las relaciones entre los objetos geométricos y descubrimos el armonioso mundo de las proporciones. A fin de razonar más claramente dejamos de lado el número-cantidad para manejar el número-longitud. Y lo hicimos, sin vanidades aparentes, con mucha destreza.

Dada una unidad, el número era su multiplicidad¹¹. De ahí que una vez representada la unidad por un segmento de recta, otro segmento de recta podía representar cualquier número y la comparación de los segmentos establecía la relación (proporción) entre ambos. El producto de un número por si mismo a.a estaba obviamente representado por el cuadrado que se podía construir sobre un segmento de longitud a (cuadrado de lado a) razón por la cual decimos hoy "a cuadrado" cuando vemos a².

En la Grecia de esos tiempos no sólo estudiamos las proporciones entre segmentos de recta, mas también nos interesamos en las relaciones que diferentes objetos como las curvas cónicas, superficies y cuerpos regulares, guardan entre ellos y con otros. Habíamos, total e imperceptiblemente, alcanzado un alto grado de civilización. Las proporciones o fracciones racionales eran producto del sofisticado nivel de abstracción al que habíamos llegado.

Pero en el ámbito científico toda seguridad es engañosa. Convencidos, como estábamos, de que el universo de todos los números era el universo de los números fraccionarios, enunciamos el famoso principio de la conmensurabilidad: "Estando dados dos números cualesquiera, siempre es posible encontrar múltiplos de ellos que sean iguales". En otros términos, pensábamos que si un hombre y un niño comienzan a andar levantando ambos el pié derecho al mismo tiempo, al cabo de un cierto tiempo estarán nuevamente en la misma situación. Y esto, aunque el hombre y el niño den pasos de diferente longitud. Nada más lógico ni más claro... ¿no es verdad?

Pero Hippasus¹², miembro de la Escuela Pitagórica, observó que tan evidente principio no es cierto. En efecto, si tratamos de evaluar la longitud de la diagonal de un cuadrado cuyo lado vale una unidad, descubriremos que el principio de conmensurabilidad es una atroz mentira. En otras palabras la longitud de la diagonal no es el cociente de dos números enteros. La relación que existe entre el lado y la diagonal de un cuadrado nos intrigó, no sólo en el seno de la Grecia clásica sino desde mucho antes, cuando en tierras de la bella Babilonia disponíamos de una aritmética bien desarrollada y un sistema numérico libre de ataduras religiosas. En ese entonces ya calculamos la raíz cuadrada de 2 con 5 decimales exactos mediante la definición de una sucesión recursiva muy ingeniosa.¹³ Obtuvimos, escrito en el sistema sexagesimal, el siguiente resultado:

"la raíz cuadrada de 2 es 1; 24, 51, 10"

que en nuestro sistema decimal es , es decir 1,414212963...

En los sutras¹⁴, el valor de la raíz cuadrada de 2 es (en sistema sexagesimal) 1; 24, 51,10,37 es decir: 1.414215818... El valor real de la raíz de 2 está entre ambos, más cerca del primero que del segundo. Pero ese precioso acto de humildad que consiste en aceptar que podemos acercarnos a la verdad tanto como queramos sin jamás llegar a alcanzarla, no formaba aún parte de nuestro patrimonio. En Grecia, amábamos la belleza y la perfección era para nosotros uno de sus ingredientes substanciales. Descubrir que no existía un número natural cuyo cuadrado sea el doble el cuadrado de otro número natural pareció echar por tierra nuestra manera de concebir un universo en el que, como toda la escuela pitagórica lo sustentaba, "todo era número".

De la relación entre la diagonal y el lado de un cuadrado surgía ante nosotros una proporción misteriosa que contradecía a la razón, una especie de valor fuera de norma... un número irracional.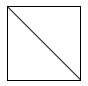
Inmediatamente comenzamos a sospechar de otra proporción que desde siempre había escapado a nuestros cálculos: la relación entre el perímetro de un círculo y su diámetro.

Este "número"¹⁵, que actualmente llamamos π, ha sabido eludir nuestra curiosidad y conservar el secreto de su irracionalidad hasta la era moderna¹⁶Pero por entonces sabíamos muy poco sobre él. En Palestina lo asimilamos al 3 un tanto para simplificar las cosas¹⁷. Como constructores de las pirámides hallamos el área de un círculo construyendo un cuadrado sobre su diámetro y disminuyéndola de de su valor.¹⁸ Mucho después, Arquímedes trabajó arduamente para conocerlo y se acercó a él más que sus predecesores gracias al método que obtuvo de Antífone: construyó polígonos regulares inscritos y circunscritos y midió sus perímetros. Gracias a él pudimos enunciar: "La longitud de la circunferencia de todo círculo es menor que 3 veces el diámetro más del mismo diámetro y es mayor que 3 veces el diámetro más del diámetro".¹⁹

Todo pasó como si, navegantes de un río cuyas aguas creíamos ser las únicas, llegásemos, llevados por el mismo río, a las puertas monumentales del océano. Los números irracionales, infinitamente más infinitos que los racionales, se presentaron así ante el espíritu humano.

(Continuará...)

 

Notas

¹Vivió hace entre 4,2 y 3,8 millones de años, pesaba entre 30 y 55 kilos, medía aproximadamente 1,2 metros, tenía un volumen cerebral de entre 400 y 500 cc, era vegetariano, no hablaba y no fabricaba instrumentos. Se lo considera el primero en nuestra estirpe.

²Muy parecido al anterior aunque de estatura ligeramente superior (1,40 m aprox.). La famosa Lusy era una afarensis.

³De más peso (unos 80 kilos), de más capacidad craneana (530 cc), más vegetariano que carnívoro, es poco probable que fabricase algunos instrumentos pero ya utilizaba un lenguaje rudimentario.

⁴Habitante de las sabanas, es el autor de los primeros instrumentos de piedra. Su capacidad craneana alcanzó los 670 cc.

⁵Pesaba entre 60 y 80 kilos, su altura era de 1,65 metros aproximadamente, fabricaba instrumentos y hablaba, dominaba el fuego. Su capacidad cerebral era de 1250 cc.

⁶Capacidad craneana: 1750 cc.

⁷En media tiene un peso de 70 kilos, 1,70 m de estatura, es omnívoro, habla mucho, fabrica de todo y su capacidad craneana es de 1400 cc, 350 cc menos que el homo neanderthalensis, del cual se separó (según la genética) hace 550.000 años

⁸Mesopotamia. Región situada entre el Tigris y el Éufrates, actualmente Irak, considerada durante mucho tiempo el lugar donde se ubicó el paraíso terrenal.

⁹La versión judía de esta epopeya sumeria pone a Noé en el centro de su relato.

¹⁰Papiro Rhind, por A. Henry Rhind el primer occidental que lo compró. Actualmente es posesión del Museo Británico. Actualmente se prefiere hacer referencia al Papiro Ahmes, lo que parece más justo.

¹¹Euclides en su obra "Elementos" define al número como "la multiplicidad de la unidad".

¹²Hippasus de Metaponto luego de tener el valor develar la falsedad del principio de conmensurabilidad, base matemático-religiosa de la Escuela Pitagórica, fue fondeado (ahogado en alta mar) como castigo a su coraje.

¹³E1 análisis numérico en tiempos de Babilonia será objeto de otro artículo.

¹⁴Textos religiosos-matemático de las indias orientales.

¹⁵Recordemos que la matemática griega sólo reconocía como números a los múltiplos de la unidad. Ni siquiera el 1 era un número de pleno derecho, menos π.

¹⁶La irracionalidad de π fue demostrada por Legendre en 1794.

¹⁷Un pasaje de la Biblia (1 Reyes 7:23) indica: "Hizo fundir asimismo un mar de diez codos de un lado al otro perfectamente redondo. Tenía cinco codos de altura y a su alrededor un cordón de treinta codos". Se trata de un cilindro de 5 codos de altura y de base un círculo cuyo diámetro mide 10 y cuya circunferencia es evaluada en 30 codos, lo que implica un valor aproximado de 3 para pi.

¹⁸3.16049...

¹⁹3.1408<π<3.1429

 

Referencias

[1] Santa Biblia. Reina Valera 95, Sociedades Bíblicas Unidas, 1999.        [ Links ]

[2] E. T. Bell. Men of mathematics. 1975.        [ Links ]

[3] David Bergamini. Mathematics. Time-Life Books, 1969.        [ Links ]

[4] Nicolás Bourbaki. Eléments d'Histoire des Mathématiques.        [ Links ]

[5] J. J. O'Connor y E. F. Robertson. An overview of Babylonian Mathematics. School fo mathematics and statistics, St. Andrews University of Scotland.

[6] O. Pino. Construcción axiomática de los números. Inédito.        [ Links ]

[7] L. Rodríguez y O. Pino. Irracionalidad y Trascendencia. Inédito.