Services on Demand
Journal
Article
Indicators
Related links
Share
Acta Nova
On-line version ISSN 1683-0789
RevActaNova. vol.2 no.1 Cochabamba Dec. 2002
Divulgación Científica
Procesos Geométricos Infinitos: Camino Hacia los Fractales
Alvaro Carrasco C.
Carrera de Matemática
Universidad Mayor de San Simón
Cochabamba, Bolivia
e-mail: acarras@fcyt.umss.edu.bo
En este trabajo mostramos que sencillos procesos geométricos como contracciones dilataciones reflexiones y traslaciones, en su iteración al infinito pueden generar objetos geométricos de gran complejidad e irregularidad, pero con gran autosimilaridad y belleza a los cuales se les llaman atractores o fractales. Se mostrará la generación de estos atractores usando el Algoritmo de Iteración Aleatorio, mediante el programa FRACTINT.
1. Preliminares matemáticos
Definición 1 Sea ƒ : Χ ![]() X una función en un espacio métrico (Χ,d), entonces:
X una función en un espacio métrico (Χ,d), entonces:
(i) el punto xƒ
Χ se llama punto fijo si ƒ(xƒ) = xƒ
(ii) se llama contractiva si existe una constante 0 ≤ s < 1 tal que
d(ƒ(x), ƒ(y)) ≤ sd(x,y)
para todo x, y
Χ, cualquier s se llama factor de contractividad.
(iii) las iteraciones de ƒ se definen recursivamente por ƒ(n+1)(x) = ƒ (ƒ(n)(x)), n = 0,1,2,..., con ƒ(0)(x) = x.
Teorema 2 Sea ƒ : Χ ![]() Χ una función contractiva en un espacio métrico completo (Χ,d). Entonces ƒ tiene exactamente un único punto fijo xƒ
Χ una función contractiva en un espacio métrico completo (Χ,d). Entonces ƒ tiene exactamente un único punto fijo xƒ ![]() Χ y para cualquier x
Χ y para cualquier x ![]() Χ, la sucesión (ƒ(n)(x)) con n = 0,1,2,... converge a xƒ.
Χ, la sucesión (ƒ(n)(x)) con n = 0,1,2,... converge a xƒ.
El teorema intuitivamente dice que una función contractiva mapea Χ en si mismo y, lo más importante, que para alcanzar su punto fijo se puede iterar la función a partir de un punto arbitrario.
Definición 3 Sea (Χ, d) un espacio métrico entonces se define el espacio de los fractales (![]() (Χ),h(d)) donde
(Χ),h(d)) donde ![]() (Χ) = {A
(Χ) = {A ![]() Χ, A ≠
Χ, A ≠ ![]() : A es compacto1} y la métrica de Hausdorff, h(A,B) = máx{d(A,B),d(B,A)}.
: A es compacto1} y la métrica de Hausdorff, h(A,B) = máx{d(A,B),d(B,A)}.
Donde d(A,B) es la distancia entre conjuntos, la cual se define por
max {min d(x, y) : y ![]() B :x
B :x ![]() A}
A}
La definición anterior dice que el espacio de los fractales se construye en función del espacio "base" Χ y sus elementos son conjuntos, además dicho espacio se hace métrico también en función de la métrica d.
Teorema 4 [2] Sea (Χ,d) un espacio métrico completo entonces (![]() (Χ),h) es completo.
(Χ),h) es completo.
La importancia de la completitud del espacio de los fractales radica en que una sucesión de Cauchy en dicho espacio siempre converge (y los fractales existen!).
Lema 5 Sea w : Χ ![]() Χ una función contractiva en un espacio métrico (Χ, d) con factor de contractividad s, entonces:
Χ una función contractiva en un espacio métrico (Χ, d) con factor de contractividad s, entonces:
(i) w mapea
(Χ) en si mismo
(ii) w:
(Χ)

(Χ) definida por w(B) = {w(x) :x
B} para todo B

(Χ), es una función contractiva en (
(Χ),h(d)) con factor de contractividad s.
El lema intuitivamente dice que teniendo una función contractiva en el espacio "base" se puede construir una función contractiva, en el espacio de los fractales.
Lema 6 Sea (Χ,d) un espacio métrico y sea {wn : n = 1,2,3,... , N} funciones contractivas en (![]() (Χ),h(d)). Sea sn el factor de contractividad de wn y sea la función W :
(Χ),h(d)). Sea sn el factor de contractividad de wn y sea la función W :![]() (Χ)
(Χ) ![]()
![]() (Χ) definida por
(Χ) definida por
W(B) = w1(B) U w2(B) U ... U wn(B)
para cada B ![]()
![]() (Χ), entonces W es contractiva con factor de contractividad s = máx{sn : n = 1,2,3,..., N}
(Χ), entonces W es contractiva con factor de contractividad s = máx{sn : n = 1,2,3,..., N}
Una función contractiva da un punto fijo en el espacio base o en el espacio de los fractales, el lema anterior indica que tenemos que la unión de funciones contractivas generan en el espacio de los fractales una función contractiva más interesante, ya que al ser unión de funciones contractivas su punto fijo no es un punto en el sentido usual, lo es considerado como un conjunto de puntos en el espacio de los fractales. De manera que un fractal2 se obtiene como punto fijo de una función contractiva en el espacio de los fractales.
Definición 7 Un Sistema de Funciones Iteradas (I.F.S.) consiste de un espacio métrico (Χ, d) junto con un número finito de funciones contractivas wn :Χ ![]() Χ. Se denotará un I.F.S. por {Χ;wn,n = 1,2,3,... ,N}.
Χ. Se denotará un I.F.S. por {Χ;wn,n = 1,2,3,... ,N}.
Nota 8 Hasta el momento se usó un espacio métrico general (Χ,d), en lo que sigue tomaremos como Χ = ![]() n con n = 2,3 es decir el plano o el espacio y la métrica d, será la Euclidiana.
n con n = 2,3 es decir el plano o el espacio y la métrica d, será la Euclidiana.
2. Atractores en el plano
Las transformaciones que usaremos en la construcción de atractores en el plano son las siguientes: dilataciones, estiramientos, rotaciones, reflecciones y traslaciones o composiciones de las mismas, los efectos de estas transformaciones se pueden ilustrar en la siguiente figura:
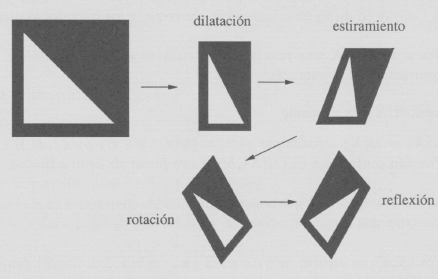
Aunque las matrices de estas tranformaciones están dadas [1], también se las puede determinar formando un sistema de ecuaciones que asocie las imágenes de los vértices de un cuadrado (por ejemplo) con las imágenes del mismo y se tendrá la transformación buscada. Se usa como conjunto iniciador un cuadrado unitario para observar los efectos de las transformaciones y garantizar la contracción de la misma.
El siguiente paso es informático pues debemos iterar este I.F.S., usando un conjunto iniciador arbitrario pues por el teorema 2 y el lema 6 sabemos de la existencia del atractor3, para esto y en adelante usaremos el programa FRACTINT4.
Este programa itera cada transformación en forma aleatoria mediante el Algoritmo de Iteración Aleatorio y al cabo de un número finito de iteraciones se van poniendo los puntos en el monitor que corresponden a los puntos fijos que definen las transformaciones, una particularidad del algoritmo es que itera con más frecuencia las transformaciones menos contractivas para llenar el fractal más rapidamente, esto se hace asociando a cada transformación un peso o probabilidad p, que corresponde a su factor de escala con relación a las otras transformaciones.
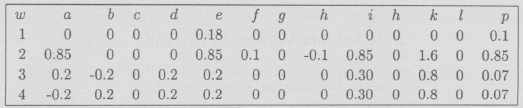
Como las transformaciones afines en el plano se escriben
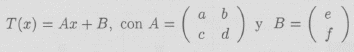
En dicho programa las funciones contractivas deben ser escritas como sigue
![]()
donde
![]()
y si es el factor de contractividad de la i-ésima transformación.
2.1. Construcción de atractores a través de I.F.S.
Como dice el viejo adagio "una imagen dice más que mil palabras", de la misma forma exponemos ejemplos con los cuales se muestra la construcción de atractores a partir de sencillos procesos geométricos y su iteración al infinito, mediante el programa FRACTINT.
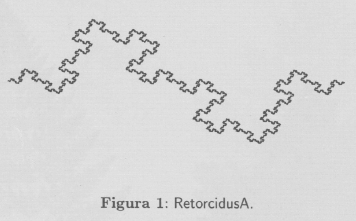
Ejemplo 1 Supongamos que un niño luego de comer su dulce, forma la siguiente figura con el palito que sostenía el dulce (que llamaremos generatriz):

Observemos que a partir del objeto iniciador el palito, se le asocia una nueva estructura. Nos preguntamos que estructura lograría si repitiese su aventura anterior en cada uno de los nueve segmentos actuales y más aún si repitiese este proceso al infinito5! Para responder esta pregunta, observemos que la estructura anterior es obtenida por la primera iteración de un I.F.S. entonces si deseamos saber sobre el conjunto obtenido por la repetición al infinito del anterior proceso geométrico tendremos que hallar el atractor de dicho I.F.S.
La descripción del mismo empieza por la siguiente observación:
Ahora observe la siguiente sucesión de transformaciones, las cuales modelan cada parte del conjunto generatriz:
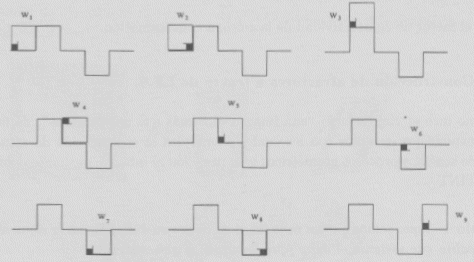
de lo anterior se sigue que el I.F.S. está constituido por las siguientes funciones:
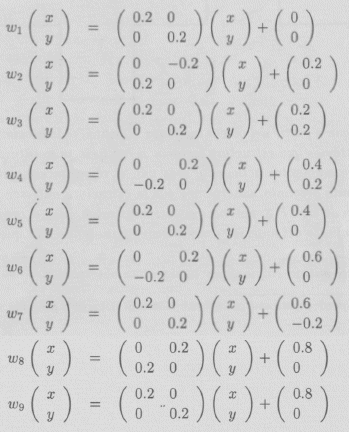
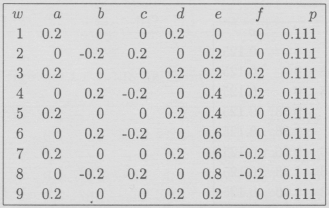
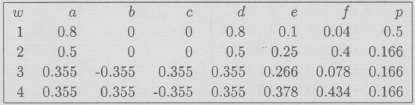
El atractor se llama "Retorcidus"; está en la sección Galería de Imágenes y el I.F.S. en la sección de Códigos.
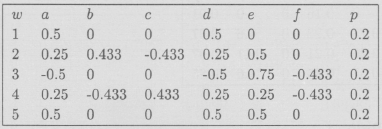
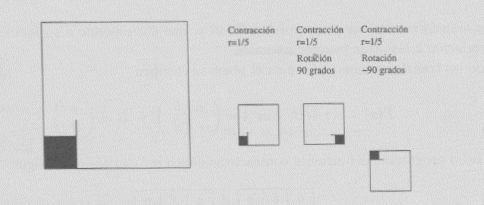
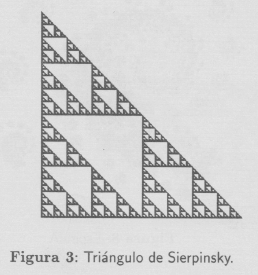
Ejemplo 2 Sea el cuadrado unitario J = [0,1]x[0,1], y consideremos las transformaciones: contracción con factor ½, contracción con factor ½ y traslación a (0.5,0) y contracción con factor ½ y traslación a (0,0.5) es decir quitar el cuarto cuadrado derecho superior. Ilustramos el efecto de estas funciones para tener idea de la formación del atractor que definen en su iteración al infinito. El atractor está en la sección de Galería de Imágenes y el I.F.S. en la sección de Códigos.
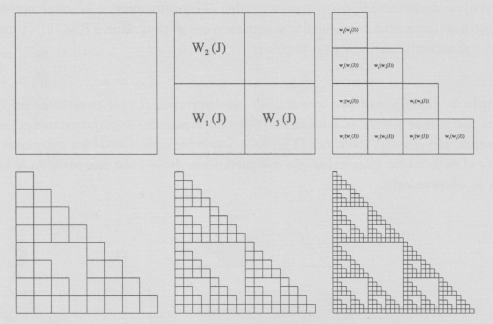
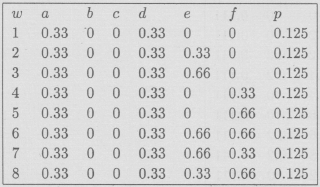
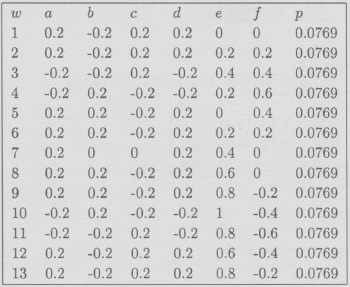
Ejemplo 3 Sea el cuadrado unitario J = [0,1]x[0,1], dividiendole en 9 cuadrados iguales consideremos las siguientes transformaciones: contracción con factor ![]() y traslación sobre todos los cuadrados, excepto al cuadrado medio, estos (nueve) procesos geométricos tienen como atractor la Esponja de Menger. El atractor está en la sección de Galería de Imágenes y el I.F.S. en la sección de Códigos.
y traslación sobre todos los cuadrados, excepto al cuadrado medio, estos (nueve) procesos geométricos tienen como atractor la Esponja de Menger. El atractor está en la sección de Galería de Imágenes y el I.F.S. en la sección de Códigos.
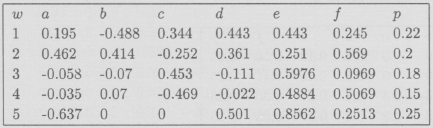
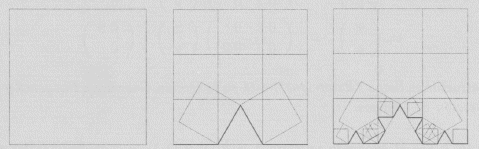
Ejemplo 4 Un ejemplo menos rígido, sea el cuadrado unitario J = [0,1]x[0,1], y consideremos las transformaciones contracción con factor ![]() ; contracción con factor
; contracción con factor ![]() , rotación en 60° y traslación hasta el punto (0.3,0); contracción con factor
, rotación en 60° y traslación hasta el punto (0.3,0); contracción con factor ![]() , rotación en -60° y traslación hasta el punto (0.5,
, rotación en -60° y traslación hasta el punto (0.5, ![]() /6); y finalmente contracción con factor
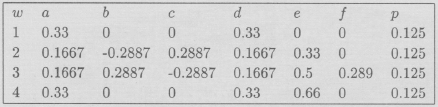
/6); y finalmente contracción con factor ![]() y traslación hasta el punto (0.66,0), estos procesos geométricos tienen como atractor la "curva" de Koch. El atractor esta en la sección de Galería de Imágenes y el I.F.S. en la sección de Códigos y en la siguiente figura se observa el efecto del I.F.S. en su segunda iteración.
y traslación hasta el punto (0.66,0), estos procesos geométricos tienen como atractor la "curva" de Koch. El atractor esta en la sección de Galería de Imágenes y el I.F.S. en la sección de Códigos y en la siguiente figura se observa el efecto del I.F.S. en su segunda iteración.
3. Atractores en el espacio
Las ideas dadas anteriormente se extienden al espacio, aunque la construcción de los atractores se haga más complicada, y alguna veces el programa FRACTINT no pueda mostrar el atractor en todo su esplendor.
Ejemplo 5 Supongamos que tenemos un cubo unitario, el cual es dividido en 27 cubos iguales por planos paralelos a los lados. Sean las siguientes transformaciones geométricas, contración con un factor de 1/3 y traslación sobre cada uno de los anteriores cubitos excepto el cubo medio y los cubos que comparten con dicho cubo una cara, en la siguiente figura se observa esto:
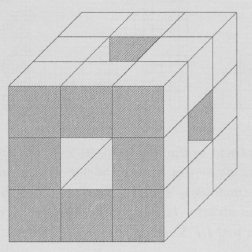
Este proceso geométrico se modela por un I.F.S. de 20 transformaciones, (¿podría escribirlas?) y el atractor llamado esponja de Sierpinsky-Menger, está en la sección Galería de Imágenes, aunque en dicho gráfico se muestra tan solo la cuarta iteración del I.F.S., las siguientes iteraciones quedan para la imaginación del lector... verdad que dicho atractor es fascinante.
4. Una aplicación: El Teorema del Collage
Teorema 9 (Barnsley 1985) Sea (Χ, d) un espacio métrico. Sea L ![]()
![]() (Χ) dado y sea ε > 0. Escojamos un I.F.S. {Χ;w0,w1,... ,wn} con factor de contractividad 0 ≤ s < 1 tal que
(Χ) dado y sea ε > 0. Escojamos un I.F.S. {Χ;w0,w1,... ,wn} con factor de contractividad 0 ≤ s < 1 tal que
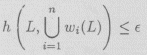
donde h(d) es la métrica de Hausdorff, entonces
![]()
donde A es el atractor del I.F.S., equivalentemente

para todo L ![]()
![]() (Χ).
(Χ).
Prueba: Por el lema 6, la función ![]() es contractiva con factor de contractividad s = max{sn : n = 1,2,3,...,N}, donde sn el factor de contractividad de wn, entonces tenemos:
es contractiva con factor de contractividad s = max{sn : n = 1,2,3,...,N}, donde sn el factor de contractividad de wn, entonces tenemos:
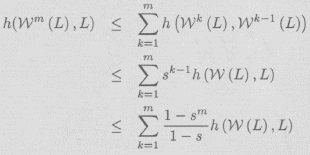
haciendo m ![]() ∞ tenemos
∞ tenemos
![]()
esto termina la prueba.
En esencia este resultado dice que dada una figura usando algunas transformaciones (las cuales actúan en el conjunto dado como conjunto iniciador) las cuales hagan un collage de la original es decir tal que la figura se recubra de la mejor forma posible, es posible reconstruirla como un atractor del algún I.F.S., pues un atractor puede tener distintos Sistemas de Funciones Iteradas que lo generen.
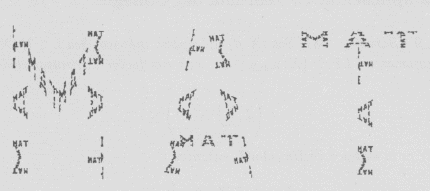
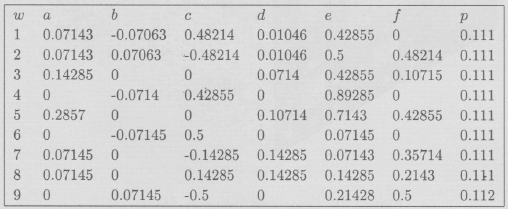
Ejemplo 6 Construimos un I.F.S. cuyo atractor sea la palabra MAT, con la ayuda de 9 transformaciones, las cuales dispuestas convenientemente darán un atractor muy próximo en la métrica de Hausdorff. La idea para esto es empezar con un cuadrado unitario como conjunto iniciador y pensar que la letra MAT está constituida de 9 rectángulos rotados trasladados etc., los cuales forman los segmentos de MAT, el I.F.S. está en la sección códigos y el atractor es el que se muestra en la imagen superior.
Observe la autosimilaridad del atractor, tenemos un acercamiento a la parte superior de la letra A:
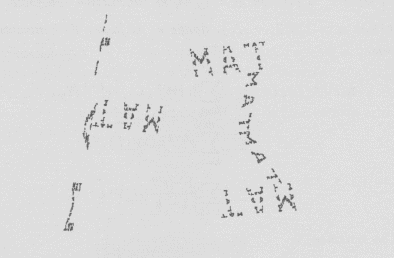
En lo que sigue se hará uso de este teorema para modelar las Hojas 1, 2 y 3. Esto se logró según la autosimilaridad de la figura y el Collage de la misma convenientemente contraída rotada y traslada, como el anterior caso el estudio de los I.F.S. explican en detalle los procesos geométricos asociados.
5. Galería de imágenes
A continuación presentamos algunos atractores, obtenidos como puntos fijos de simples transformaciones geométricas.












6. Códigos de I.F.S.
En esta sección están los I.F.S. de todos los atractores de la sección anterior exceptuando la Esponja de Menger-Sierpinsky. Algunos nombres de los siguientes atractores no corresponden a la consonancia latina, ellos son solo nombres.
Código del I.F.S. de RetorcidusA
Código del I.F.S. de la Curva de Koch
Código del I.F.S. de MAT(A)
Código del I.F.S. del Triángulo de Sierpinski
Código del I.F.S. de la Carpeta de Menger
Código del I.F.S. de Hoja 1
Código del I.F.S. de Hoja 2
Código del I.F.S. del PulpoA
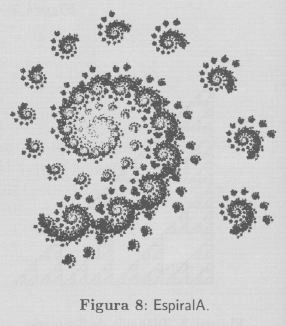
Código del I.F.S. de La EspiralA
Código del I.F.S. del DragonA
Código del I.F.S. de La Hoja 3
Código del I.F.S. de HislasA
Código del I.F.S. de TriangulusinfinitumA
Código del I.F.S. de GemelusA
Código del I.F.S. del Árbol
Código del I.F.S. del Helecho 3D
Notas
1Un subconjunto compacto en un espacio métrico es cerrado y acotado.
2Los fractales no se definen en general y se acepta la definición de ser conjuntos tales que su dimensión fractal es menor que su dimensión topológica (B. Mandelbrot).
3En lo que sigue no haremos distinción entre punto fijo, atractor y fractal.
4Este programa está catalogado el número uno en genaración de fractales y se encuentra al alcance de todos en internet.
5Es claro que no puede repetir este proceso al infinito, sin embargo la pregunta se hace en el contexto matemático.
Referencias
[1] Banchoff y Wermer. Linear Algebra Through Geometry. Springer - Verlag, 1992.
[2] M. Barnsley. Fractals Everywhere. Academic Press, segunda edición, 1993.
[3] A. Carrasco. Sistemas de Funciones Iteradas y Dimensión Fractal. U.M.S.S., 1996. [ Links ]
[4] G. Contreras. Computación grafica y sistemas dinámicos. Revista Matemática Universitaria (S.B.M.), (11), 1990.
[5] B. Mandelbrot. La geometría fractal de la naturaleza. Tusquets, Barcelona, 1987. [ Links ]
[6] D Saupe, H. Peitgen, y H. Jürgens. Fractals for the Classroom. Springer-Verlag, 1992.