Artículo Científico

 

Estudio de la Estructura Tridimensional de Proteínas Mediante la Geometría Fractal

 

 

Sergio Gómez González¹, Joan Grau Barceló², Ricardo Torres Camara², Francesc Sepulcre Sánchez³

¹ Departamento de Expresión Gráfica en la Ingeniería
² Unidad Estructural de Mecánica de la Escuela Universitaria de Ingenieros Técnicos Industriales de Barcelona
³ Unidad Estructural de Química Industrial de la Escuela Universitaria de Ingenieros Técnicos Industriales de Barcelona

Universidad Politécnica de Catalunya
Comte d'Urgell 187
08036 Barcelona - Spain
e-mail: Francesc.Sepulcre@upc.es

 

 

---

Resumen

En el presente trabajo se realiza un estudio de caracterización de estructuras secundarias de las proteínas mediante la geometría fractal. Esta geometría se presenta como un método capaz de diferenciar los grados de compactación (estructura terciaria) de las proteínas y sus elementos de estructura secundaria. Las ventajas más importantes de la aplicación de esta geometría son su fácil implementación y la posibilidad de cuantificar, y por tanto diferenciar, el grado de empaquetamiento de estructuras irregulares tridimensionales, como por ejemplo las proteínas.

Palabras Clave: Estructura de proteínas, geometría fractal, dimensión fractal, box-counting.

---

 

 

1. Introducción

Un fractal viene a ser el producto final que se origina a través de la iteración infinita de un proceso geométrico bien especificado. Este proceso geométrico, que es generalmente de naturaleza muy simple, determina perfectamente la estructura final que, muy frecuentemente, debido a la repetición infinita que se ha efectuado, tiene una complicación aparentemente extraordinaria.

Los fractales, por lo tanto, son conjuntos geométricos frecuentemente complicados en apariencia, pero en realidad resultan ser tales que para su descripción, construcción y exploración se requiere muy poca información. También es cierto que para la introducción de los objetos clásicos de la geometría, la circunferencia, el triángulo,... la información requerida es muy simple, pero ésta proporciona el objeto al que se refiere todo de una vez. Lo característico de las estructuras fractales consiste en la iteración infinita del proceso simple que da lugar al objeto en cuestión.

La esencia de la teoría es que muchas estructuras naturales, como por ejemplo las nubes, que aparentan tener una complejidad extraordinaria, poseen en realidad una misma regularidad geométrica: la denominada invarianza bajo escala. Esto significa que, si se analizan estas estructuras a distintas escalas, se encuentra una y otra vez los mismos elementos básicos. Su exploración a distintas escalas encuentra una descripción matemática apropiada mediante el concepto de dimensión fractal.

Todo esto se pone de manifiesto en un modelo matemático descubierto por Mandelbrot en 1980 y conocido hoy como el Conjunto de Mandelbrot [6]. Este objeto de gran complejidad presenta una riqueza extraordinaria de formas y estructuras que consta de fragmentos geométricos de orientación y tamaño variable, pero de aspecto similar (ver Figura 1).

 

2. Dimensión fractal

Una de las características principales de cualquier objeto fractal es su dimensión fractal (d_f), que mide su grado de irregularidad e interrupción. No obstante, al contrario de la dimensión Euclídea, la dimensión fractal puede muy bien ser una fracción simple, como 1/2 ó 5/3, e incluso un número irracional, como log4/log3, -1.2658 ó π. Así resulta útil decir que para ciertas curvas planas muy irregulares la dimensión fractal está entre 1 y 2, o decir que para superficies muy hojaldradas e irregulares la dimensión fractal es intermedia entre 2 y 3.

Uno de los métodos más extendidos en el cálculo de la dimensión fractal es el box-counting o recuento por cajas. La idea central por la que se llega a este concepto de dimensión consiste en diseñar un proceso de medida a una cierta escala δ, que ignora las irregularidades de tamaño menor y estudia cómo varía dicha medida a medida que δ tiende a cero.

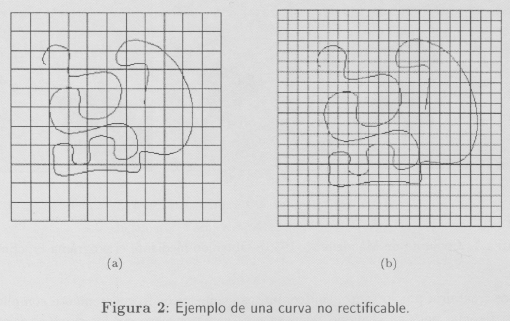
Para ilustrar mejor el concepto de la dimensión fractal obtenida por el método de recuento por cajas podemos imaginarnos una curva E, no necesariamente rectificable. Si reticulamos el plano con cuadrados de lado δ (ver Figura 2) podemos definir "δ longitud de C" (longitud que aprecia solamente detalles de tamaño menor que δ) como la suma de las longitudes de los lados de los cuadrados del mallado que cortan a la curva C, y así, si el número de éstos es N_δ(C), tal δ-longitud sería:

Si la curva es rectificable, cabe esperar que cuando δ tiende a cero el número L_δ(C) tienda a la longitud de dicha curva, pero se si trata de una curva que mirada a cualquier escala sigue mostrando irregularidades, es decir una curva de dimensión mayor que uno, cuando hagamos tender δ a cero L_δ(C) tenderá a infinito. La velocidad con la que lo hace, que de alguna forma da el grado de irregularidad, o más bien el tamaño de la curva, puede ser medido por el número s para el cual L_δ(C) y δ^-s crecen con velocidades comparables, simbólicamente cuando δ → 0.

con K y s constantes. Por lo tanto, tomando logaritmos, log L_δ(C) ≈ log δ para δ pequeños. O en términos más precisos

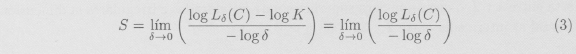
ya que el numerador y el denominador tienden a infinito y log K es constante. Esto motiva la introducción de un nuevo concepto de dimensión.

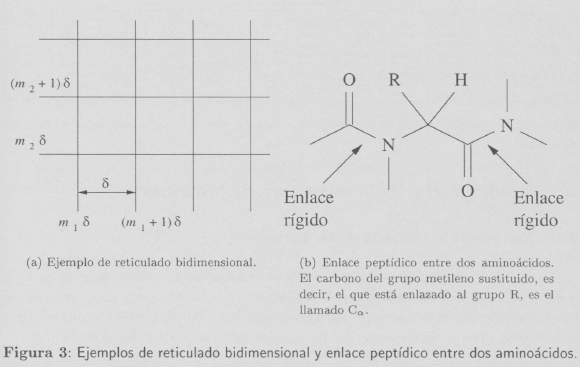
En ⁿ consideramos la δ-malla formada por la colección de "cubos" de la forma:

donde m₁ ... m_n son enteros.

Si estamos por ejemplo en ², se tiene la malla que se ilustra en la Figura 3(a).

Se define la dimensión del recuento por cajas de un conjunto E como

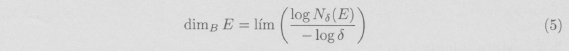
donde N_δ(E) es el número de cubos de la δ-malla que corta a E, en el caso de que dicho límite exista.

En los fenómenos físicos o en las estructuras físicas reales que se pueden describir mediante un modelo fractal (agregados moleculares, curvas de separación de medios, difusión, polímeros, etc.) no tiene sentido la expresión δ → 0 y lo que se hace en la práctica es calcular N_δ(E) para valores pequeños de δ, siendo el término "pequeño" variable según el contexto.

En tales casos, si se representa en un sistema de ejes coordenados el número log N_δ(E) en función de —log δ, resulta, cuando δ varía dentro de valores adecuados a cada caso, un conjunto de puntos que se aproximan a una recta cuya pendiente nos da la dimensión fractal del recuento por cajas.

 

3. Estudio fractal de la estructura de proteínas

3.1. Estructura secundaria de las proteínas

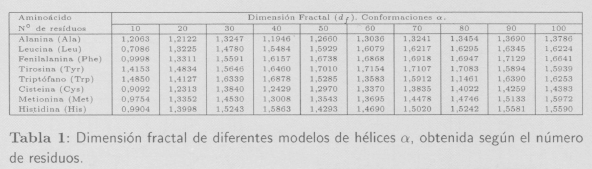
La estructura secundaria de una proteína se define como la conformación local de su cadena polipeptídica (backbone). Aproximadamente una tercera parte de los enlaces polipeptídicos de una proteína son rígidos, por lo que dicha cadena puede imaginarse como una serie de planos rígidos separados por grupos metileno sustituidos (Figura 3(b)).

La rigidez de estos enlaces impone ciertas restricciones al número de conformaciones espaciales que la cadena polipeptídica puede adoptar. La conformación de una cadena polipeptídica queda, por tanto, definida en función de los ángulos que adopten los enlaces N - C_α Phi(Φ) y C_α-C Psi (Ψ), que no son rígidos.

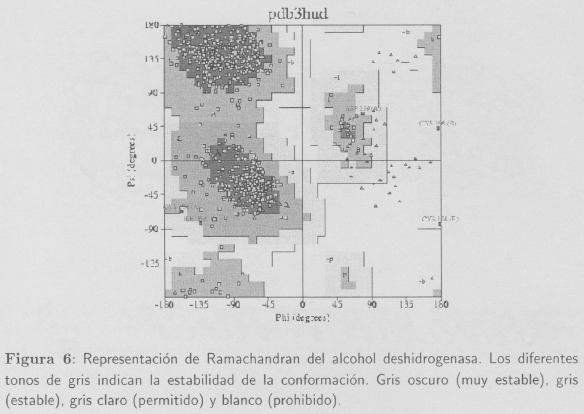
Los valores que pueden tomar estos ángulos, que están restringidos por las interacciones electroestáticas y los impedimentos estéricos que aparecen en la proteína, se sumarizan en los diagramas de Ramachandran (Figura 6). Así, en estos diagramas se diferencian zonas que corresponden a los valores de Φ y Ψ permitidos, y otras zonas que corresponden a los valores prohibidos de estos ángulos.

En función de los valores de estos ángulos se pueden diferenciar principalmente dos tipos de estructuras secundarias en las proteínas (ver Figura 6): hélices α (Φ = -57°; Ψ = -47°, y 3.6 aminoácidos por vuelta de hélice) y láminas β(Φ = Ψ = ±180°).

3.2. Metodología

Aunque, desde un punto de vista estrictamente formal, una proteína no es un objeto fractal, ya que no presenta una misma regularidad geométrica que sea invariante bajo cambio de escala, es posible estudiar su geometría, las irregularidades de su conformación, su grado de compactación, etc., mediante este tipo de geometría.

La geometría fractal ha sido utilizada como un método de cálculo para diferenciar las estructuras secundarias y terciarias de las proteínas, así como una herramienta que puede describir el grado de empaquetamiento adquirido por hélices α, estructuras β, hélices α_3,10, etc.

En este trabajo hemos cuantificado las conformaciones tridimensionales de la estructuras polipeptídicas α y β generadas por ordenador mediante el software HyperChem [4].

Por otro lado se han obtenido secuencias de proteínas así como sus coordenadas atómicas (definidas por difracción de rayos X y por Resonancia Magnética Nuclear) de la base de datos del Brookhaven National Laboratory, EUA (Protein Data Bank) [8].

Para calcular la d_f de la estructura de proteínas mediante el recuento por cajas hemos desarrollado un software que generaliza a 3 dimensiones (³) los conceptos explicados anteriormente. Concretamente el programa realiza los siguientes pasos:

1. Se genera un cubo de arista a en el que se inserta completamente toda la proteína o estructura secundaria objeto de estudio.

2. Se realizan divisiones sucesivas de la arista (dividiendo por la mitad), con lo que se van obteniendo 1,8,64,512,... cubos sucesivamente, y después de cada subdivisión se cuenta el número de cubos que contienen como mínimo un átomo de la proteína o estructura proteica.

3. Se representa el logaritmo del número de cubos contabilizados en el paso anterior en función del logaritmo del número de subdivisión. El resultado es una recta.

4. Se realiza un ajuste por mínimos cuadrados. La pendiente de la recta obtenida es la dimensión fractal de la estructura.

3.3. Resultados

3.3.1. Cálculo de la d_f de modelos polipeptídicos (hélices α y estructuras β)

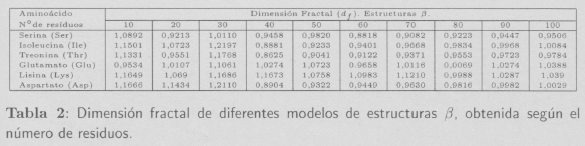
Para la primera parte del estudio se han generado hélices α y estructuras β compuestas por unidades de 10 a 100 residuos y formadas por repetición de aminoácidos. Debido a la imposibilidad de generar verdaderas láminas β (diferentes cadenas polipeptídicas dispuestas una al lado de otra de forma paralela o antiparalela), se ha optado por generar lo que llamamos estructuras β, que corresponden a una única cadena de aminoácidos. Una vez realizados los modelos y obtenidas las posiciones atómicas se ha calculado la d_f. Los resultados obtenidos se presentan en las Tablas 1 y 2.

 

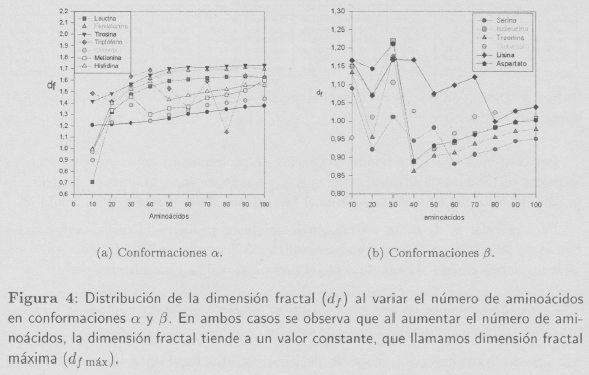
En la gráfica de la Figura 4 se ha representado la distribución de la dimensión fractal (d_f) al variar el número de aminoácidos para las conformaciones α y β.

Los resultados obtenidos ponen de manifiesto la relación existente entre el volumen de las cadenas laterales y la dimensión fractal en ambas conformaciones (hélices α y estructuras β).

Al aumentar el volumen de los aminoácidos, aumenta la d_f, comportamiento descrito por Daoud y Martin [1] para polímeros y que según los resultados obtenidos puede ser aplicado a las estructuras secundarias de proteínas.

En los dos modelos, a medida que aumenta el volumen de los aminoácidos se observa un empaquetamiento mayor, un mayor volumen y un aumento de la d_f.

Las diferencias obtenidas entre las hélices α y las estructuras β se deben a las conformaciones espaciales. Las hélices α están más empaquetadas y las fuerzas de repulsión son mayores, mientras que en las estructuras β las repulsiones entre las cadenas son mucho menores y se encuentran menos empaquetadas. Por lo que la d_f de las hélices α son mayores que la d_f de las estructuras β.

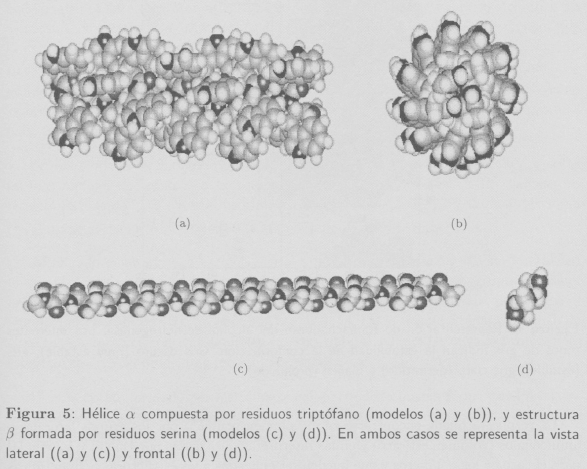
En la Figura 5 se representa un modelo de hélice a formada por residuos de triptófano (Trp) y un modelo de una estructura β compuesta por residuos de serina generados por ordenador.

Para generar los modelos de hélice a los ángulos Φ(N — C_α) y Ψ(C — C_α) empleados en el estudio han sido: Φ = Ψ = -135°, Φ = Ψ = -90°, Φ = Ψ = -45°, Φ = Ψ = 0º, Φ = Ψ = +135°, Φ = Ψ = +90° y Φ = Ψ = +45°. Los aminoácidos utilizados son: alanina (Ala), glicocola (Gly), leucina (Leu), fenilalanina (Phe), tirosina (Tyr), triptófano (Trp), cisteína (Cys), metionina (Met) e histidina (His).

La variación del valor de los ángulos Φ y Ψ desde -135° hasta +135° genera hélices con distinto paso (o avance por residuo), creando hélices compactas en algunos casos, o hélices estiradas a modo de zig-zag en otros.

Las conformaciones de las cadenas polipeptídicas son estudiadas mediante la descripción de cada uno de los residuos de aminoácidos en el gráfico bidimensional de Ramachandran. En el gráfico de la Figura 6 se sitúan los residuos entre los ángulos -180° < Φ < +180° y -180° <Ψ< +180° y se muestran las conformaciones más normales observadas en las cadenas polipeptídicas.

En este trabajo el rango de ángulos utilizados ha sido ligeramente inferior a los rangos habituales en los diagramas de Ramachandran, pero se indica el intervalo de las áreas o zonas permitidas de mayor interés. Así, se incluyen en el estudio los ángulos de torsión Φ y Ψ para las estructuras más importantes (hélices α dextrógira, hélices α levógira, estructuras β paralelas, estructuras β antiparalelas, hélices 3₁₀ y hélices del colágeno).

En los modelos estudiados se observa que aquellos que han sido generados con aminoácidos de bajo volumen (volumen estérico), como es el caso de la alanina y la glicocola, se obtienen d_fmáx para los ángulos Φ = Ψ = —45° y Φ = Ψ = +45°. En cambio, para los modelos generados con aminoácidos con mayor volumen estérico, como el triptófano, cisteína, metionina, histidina y fenilalanina, se obtiene un d_fmáx para los ángulos Φ = Ψ = -90° y Φ = Ψ = +90°.

¿Por qué los modelos generados por aminoácidos como Trp, Cys, Met, His y Phe no tienen d_fmáx a Φ = Ψ = -45° y Φ = Ψ = +45°?

La respuesta puede encontrarse en el volumen ocupado por los grupos laterales o aminoácidos (volumen estérico) y en las interpretaciones dadas por Daoud y Martin [1] para el caso de los polímeros y que pueden ser aplicadas a las estructuras polipeptídicas estudiadas por nosotros.

En los modelos polipeptídicos generados con alanina y glicocola para los ángulos Φ = Ψ = -45° y Φ = Ψ = +45°, se observa una d_f máx as 1,4 (d_{f ala} = 1,41 y d_{f gly} = 1,35) que corresponde con el máximo empaquetamiento de la molécula.

La conformación más estable observada según los diagramas de Ramachandran corresponden a los modelos polipeptídicos generados con Φ = Ψ = —45° y que poseen mayor d_f, ya que sus residuos están situados en las zonas más favorables.

Para los polipéptidos generados con cadenas laterales de menor volumen estérico se observa cómo las conformaciones generadas con Φ = Ψ = +45° y Φ = Ψ = —45° se encuentran más empaquetadas y con menor distancia entre las cadenas laterales en cada una de las vueltas. A medida que el volumen estérico de las cadenas laterales aumenta, las repulsiones entre los grupos situados en vueltas contiguas aumenta y la conformación más estable es aquella que posee mayor paso o distancia entre residuos.

Los modelos creados con los aminoácidos fenilalanina, triptófano, metionina, histidina y cisteína obtienen d_{f máx} para los ángulos de rotación Φ = Ψ = —90° y Φ = Ψ = +90°.

Cuando el volumen de la cadena lateral es considerable provoca la mayor estabilidad del polipéptido a ángulos de rotación mayores que con la alanina y la glicocola.

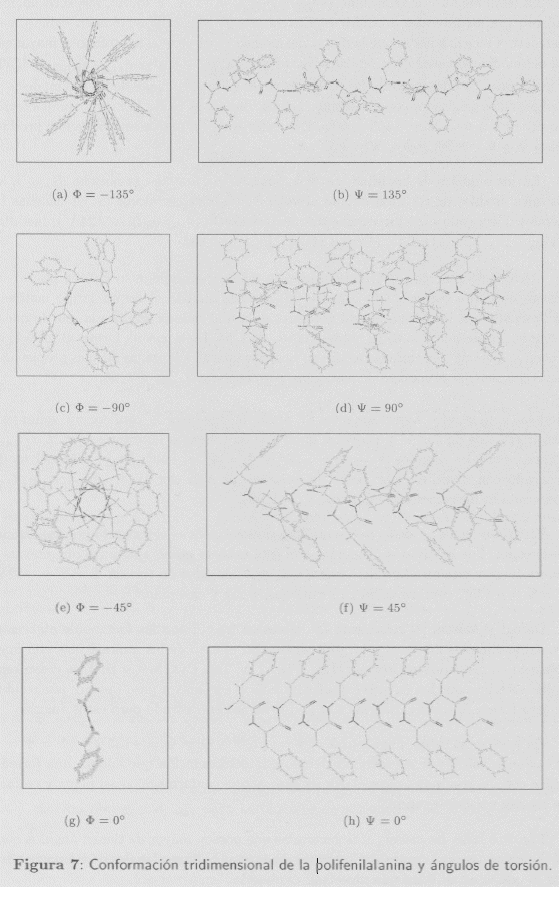
La fenilalanina y el triptófano (V_{Van der Waals} = 135ų y 163ų, respectivamente) poseen grupos laterales aromáticos. El triptófano tiene mayor volumen debido a su estructura bicíclica por lo que la d_{f máx} del modelo generado con triptófano es mayor que la del modelo generado con fenilalanina. (d_{f máx (Trp)} = 1,61 y d_{f máx (Phe)} = 1,56). Las Figuras 7 y 8 representan las conformaciones tridimensionales de los dos modelos de polipéptidos generados con éstos aminoácidos. En ambos casos, la mayor compactación se produce a Φ = Ψ = —45° y Φ = Ψ = +45°, pero la mayor estabilidad se produce para Φ = Ψ = -90° y Φ = Ψ = +90°.

 

En los modelos de histidina, cisteína y metionina también se obtiene d_{f máx} a los mismos ángulos de rotación debido al volumen de Van der Waals de las cadenas laterales. Para cada caso los valores son: metionina (V_{Van der Waals} = 124ų), histidina (V_{Van der Waals} = 118ų) y cisteína (V_{Van der Waals} = 86ų).

Al modelo generado con aminoácidos de metionina, aunque su cadena lateral sea lineal, el azufre contenido le confiere un volumen similar al de un grupo metileno, provocando que la cadena lateral sea parecida a una cadena ramificada, por lo que el volumen es elevado y la d_{f máx} obtenida sea de 1,54. De la misma forma, el modelo de cisteína, que también contiene azufre en su grupo lateral, adopta las mismas propiedades estructurales que el modelo de metionina pero con una d_{f máx} = 1, 28.

El polipéptido formado por histidina se comporta de la misma forma que los cuatro modelos comentados anteriormente. Su anillo de imidazol le confiere un volumen de Van der Waals de 118Á³ y provoca, igual que en los casos anteriores, que la d_{f máx} se obtenga para los ángulos Φ = Ψ = —90° y Φ = Ψ = +90°. En el caso del modelo generado con histidina, por tener un volumen de Van der Waals inferior, la d_{f máx} observada es ligeramente menor (d_{f máx} = 1,59).

El último de los modelos polipeptídicos a estudiados es el formado por aminoácidos de tirosina. Los resultados obtenidos con éste modelo no se ajustan a ninguno de los anteriormente citados. Adquiere una d_{f máx} para ángulos de torsión Φ = Ψ = —135° y Φ = Ψ = +135°; conformación en forma de zig-zag y casi plana.

Daoud y Martin [1] relacionan la dimensión fractal con las fuerzas de atracción y repulsión (fuerzas de corto y largo alcance). En el caso de los aminoácidos con mayor volumen en las cadenas laterales (Leu, Phe, Tyr, Trp, Cys, Met y His), se crean repulsiones estéricas que hacen más estables las hélices con mayor paso (avance por residuo), de esta forma se justificarían las d_{f máx} que hemos encontrado para estos ángulos.

En los demás casos, ángulos (Φ = Ψ = -135° y Φ = Ψ = +135°) y (Φ = Ψ = 0^o) se obtienen valores de d_f menores debido a la conformación que adopta una forma de hélice con un gran paso, para el primer caso, y una conformación casi plana y en forma de zig-zag para el segundo.

Por otro lado, las estructuras generadas que poseen mayor d_f tienen ángulos que se sitúan en zonas muy favorables sobre los diagramas bidimensionales de Ramachandran, por lo que la estabilidad que muestran es elevada.

3.3.2. Cálculo de la d_f de proteínas

Proteínas formadas mayoritariamente por hélices α o láminas β

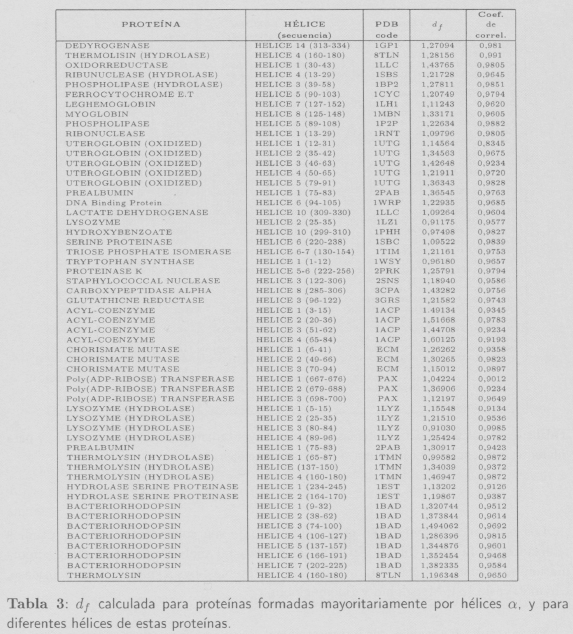
La tercera parte del estudio se ha centrado en la selección de proteínas del PDB (Protein Data Bank [8]) que contengan mayoritariamente un sólo tipo de estructura secundaria (hélice α o estructura β), y se ha calculado la d_f para cada una de esa proteínas, así como únicamente para cada una de las secuencias de aminoácidos correspondientes a la conformación mayoritaria dentro de la proteína, descartando el resto de estructuras. Algunos de los resultados obtenidos para las más de 100 proteínas estudiadas se indican en las Tablas 3 y 4. Los resultados obtenidos para el caso de la hélice α se muestran en la Tabla 3.

 

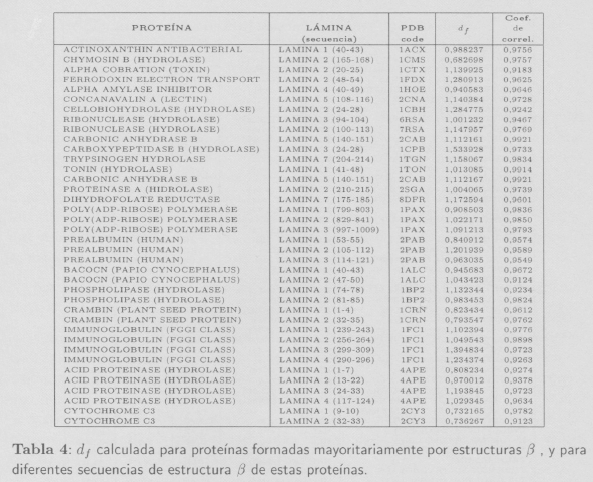
Los resultados obtenidos para las proteínas formadas mayoritariamente por estructuras β se muestran en la Tabla 4.

Isogai e Itoh [5] también demuestran que es posible asignar dimensiones fractales características a las proteínas que mayoritariamente están formadas por hélices α o estructuras β. En sus estudios concluyen que las proteínas con conformaciones α poseen una dimensión fractal d_f = 1,38, mientras que las proteínas con conformaciones mayoritariamente (5 presentan una dimensión fractal ligeramente menor (d_f = 1,29). En nuestro caso los valores promedio encontrados son: d_f = 1,2490 ± 0,0417 para hélices α y d_f = 1,0451 ± 0,0601 para estructuras β.

Los resultados obtenidos en este trabajo difieren un poco de los obtenidos por Isogai e Itoh [5]. Esta diferencia podría ser debida básicamente a dos motivos. En primer lugar, en este trabajo se han tratado hélices α y estructuras β individualmente y no como conjunto de una proteína completa. Isogai e Itoh [5] estudian proteínas (mayor número de átomos) que están compuestas mayoritariamente por hélices o estructuras, pero que también tienen un elevado porcentaje de otro tipo de estructuras secundarias, como por ejemplo turns y/o estructura desordenada. En segundo lugar, el método utilizado en ambos trabajos es claramente diferente.

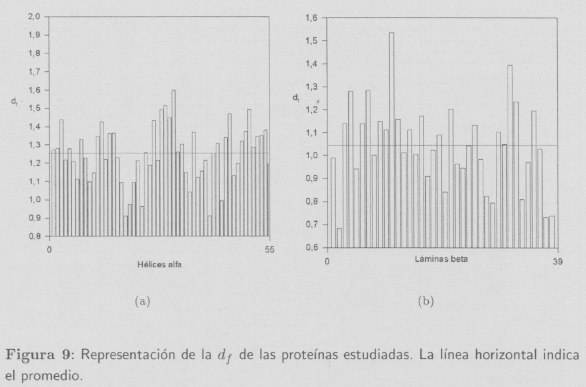
En la Figura 9 se muestra la d_f de cada una de las estructuras α y β así como el valor promedio obtenido. Mientras que las 55 estructuras α estudiadas tienen un promedio de d_f = 1,2490 ± 0,0417, las 39 estructuras β estudiadas toman un promedio inferior y equivalente a d_f = 1,0451 ± 0,0601. Las estructuras α se encuentran entre 0,91 < d_f < 1,67, mientras que las estructuras β se sitúan entre 0,68 < d_f < 1,54.

El número de hélices y estructuras que se han tratado en este trabajo es muy superior al utilizado por Isogai e Itoh [5], por lo que los promedios obtenidos deben ser más precisos.

Isogai e Itoh [5] interpretan las diferencias de d_f entre las hélices y las estructuras debido a las fuerzas estéricas de repulsión y atracción entre los átomos vecinos, que es la misma conclusión a la que llegan Daoud y Martin [1]. Por su disposición en el espacio, las hélices sufren fuerzas de repulsión estérica entre sus cadenas laterales, mientras que en las estructuras con una disposición en zig-zag, las fuerzas estéricas son mucho menores.

Proteínas formadas por hélices α y láminas β

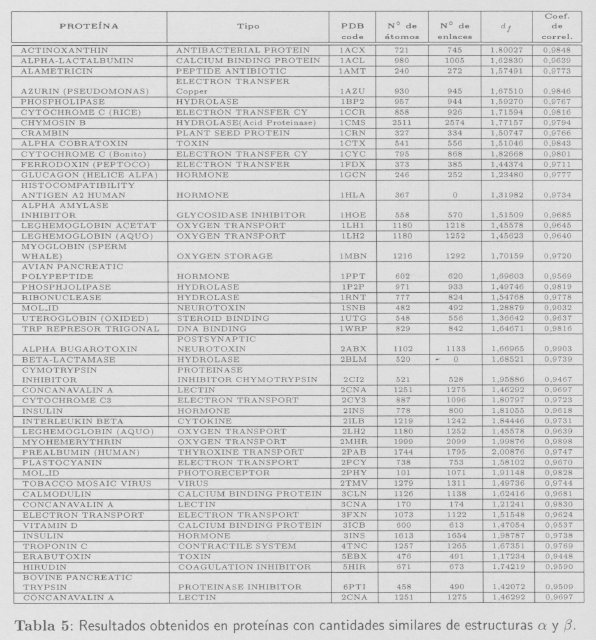
De la misma forma que se ha procedido en el apartado anterior, y con el objetivo de complementar estos resultados, hemos estudiado la dimensión fractal de proteínas que contienen cantidades aproximadamente iguales de estructuras α y β.

En la Tabla 5 se presentan los resultados obtenidos para algunas de las proteínas estudiadas, que en este caso contienen cantidades similares de estructuras α y β.

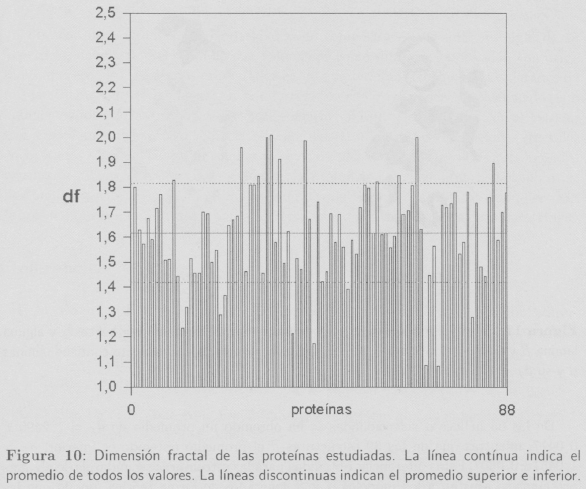
Tal y como puede verse en la Figura 10, la d_f de las proteínas estudiadas se encuentra distribuida entre 1 ≤ d_f ≤ 2. El valor promedio es d_f = 1,6186 ± 0,0431. Los límites superiores e inferiores son d_f = 1,82 y d_f = 1,42, respectivamente (para un intervalo de confianza del 95%).

Los resultados obtenidos en el presente trabajo son coincidentes con los estudios realizados por Li HQ y col. [3]. En su artículo: "Fractal analysis of protein chain conformation" se calcula la dimensión fractal de cinco proteínas: Lysozyme, Carboxypeptidase, Chymotrypsin (a), Myoglobin y Haemoglobin.

Estos resultados pueden ser interpretados de la misma forma que se interpretan las d_f de las estructuras secundarias (hélices y estructuras). Las proteínas que tienen una d_f inferior a 1,50 son aquellas que ocupan menos volumen y por lo tanto las fuerzas de atracción son mayores que las de repulsión. Las proteínas con una d_f superior a 1,50 ocupan mayor volumen y las fuerzas de repulsión son mayores que las de atracción. Y las proteínas con d_f ≈ 1,5 son las que poseen fuerzas de atracción y repulsión compensadas, teniendo en cuenta que las fuerzas son de largo y corto alcance.

Por otro lado, y según los resultados presentados en los dos apartados anteriores, la d_f obtenida en cada una de las proteínas está en relación directa al porcentaje de hélices α y estructuras β. Las proteínas con d_f> 1,5 son las que poseen mayor porcentaje de hélices, ya que por su distribución espacial aparecen más compactadas, ocupan mayor volumen. Las proteínas con d_f < 1,5 tienen mayor proporción de estructuras β y las proteínas con d_f ≥ 1,5 tienen porcentajes proporcionales de hélices y estructuras.

 

4. Conclusiones

Desde un punto de vista estrictamente matemático la proteínas no son objetos fractales, pero es posible estudiar su estructura tridimensional utilizando este tipo de geometría.

Los resultados de este trabajo demuestran que es posible caracterizar y diferenciar las hélices α y las estructuras β con un índice fractal diferente. Así mismo, se ha encontrado que las proteínas que están formadas mayoritariamente por estructuras α tienen una dimensión fractal mayor que las que están formadas mayoritariamente por estructuras β.

En el estudio realizado mediante la generación por ordenador de modelos de polipéptidos α y β con diferente número de aminoácidos se observa un aumento de la d_f a medida que aumenta el número de aminoácidos, hasta alcanzar un cierto valor constante. Las diferencias de d_f obtenida para cada uno de los modelos α y β generados con distintos aminoácidos es debida al volumen estérico de la cadena lateral, propia de cada aminoácido. Se observa cómo a medida que el volumen estérico es mayor, la d_f también lo es.

Los modelos polipeptídicos α y β generados obtienen d_f diferentes debido a los tipos de conformación tridimensional que adoptan cada uno. La d_f obtenida en los modelos polipeptídicos α son mayores que la obtenida en los modelos β. Los modelos α tienen estructuras más voluminosas, las hélices se encuentran más empaquetadas y las fuerzas de repulsión son mayores. Por el contario, los modelos β adoptan conformaciones tipo zig-zag, en las que el volumen ocupado y el empaquetamiento es menor.

En los modelos que han sido generados con aminoácidos que poseen grupos laterales poco voluminosos y con bajo volumen estérico, como es el caso de la glicocola y la alanina, la d_f máxima se ha obtenido para los ángulos (Φ = Ψ = —45° y Φ = Ψ = +45°). Sin embargo, en los modelos polipeptídicos a generados con residuos de mayor volumen estérico, la d_f máxima obtenida coincide con los modelos generados con ángulos (Φ = Ψ = -90° y Φ = Ψ = +90°). Éste último caso es representativo de los modelos α creados con fenilalanina, triptófano, metionina, histidina y cisteína.

La diferencia de la d_f máxima que se obtiene para los ángulos (Φ = Ψ = -45° y Φ = Ψ = +45°) y (Φ = Ψ = -90° y Φ = Ψ = +90°) puede interpretarse a partir de las observaciones realizadas por Daoud y Martin [1] para el caso de los polímeros. Estos autores identifican los valores obtenidos de d_f con las fuerzas de atracción y de repulsión (tanto de corto como de largo alcance). Los modelos creados con aminoácidos cuyas cadenas laterales poseen gran volumen estérico (Leu, Phe, Tyr, Cys, Met y His), crean repulsiones estéricas que hacen más estable las hélices con mayor paso (avance por residuo), mientras que los modelos que poseen aminoácidos con cadenas laterales menos voluminosas, crean hélices más empaquetadas y con paso entre residuo menor.

En el mismo estudio se ha observado cómo todos los modelos α medidos tienen d_f iguales para los ángulos de torsión (Φ = Ψ) de diferente signo. El resultado obtenido es lógico ya que la geometría fractal y la aplicación del método box-counting estudia su grado de irregularidad, considerando todas las escalas, y busca aspectos geométricos invariantes con el cambio de la misma. El hecho de obtener la misma d_f en modelos con ángulos de torsión Φ = Ψ con signos opuestos demuestra que la medida de la d_f indica el grado de irregularidad y compactación y no da información sobre el ángulo de giro (d y 1) en la formación del polipéptido.

Los estudios realizados con estructuras secundarias (hélices α y estructuras β) seleccionadas entre las estructuras terciarias de las 88 proteínas resueltas mediante difracción de rayos X y Resonancia Magnética Nuclear (PDB), demuestran que cada una de estos tipos de estructura secundaria pueden caracterizarse con una dimensión fractal diferente.

De las 55 hélices α seleccionadas se ha obtenido un promedio de d_f = 1,2490 ± 0,0417, mientras que de las 39 estructuras β el promedio obtenido es inferior, d_f = 1,0451 ±0,0601. Estas diferencias obtenidas para las estructuras secundarias de algunas proteínas se ajustan a los modelos α y β generados de forma teórica, por lo que las diferencias entre la d_f de los dos tipos de estructura pueden interpretarse de la misma forma.

El estudio fractal realizado con las 88 proteínas completas seleccionadas del Protein Data Bank indica que la d_f se encuentra distribuida entre 1 y 2. El valor promedio obtenido es d_f = 1,6186 ± 0,0431, con un margen de confianza del 95%, resultados semejantes a los obtenidos por Li HQ y col. [3].

El mismo estudio muestra que es posible identificar proteínas que mayoritariamente están compuestas por estructuras α o β. Aunque no se ha encontrado una relación directa entre el porcentaje de estructuras secundarias y la d_f, puede afirmarse que las proteínas con mayor proporción de estructuras α tienen d_f mayores que las proteínas con estructuras β. Los promedios obtenidos en éste trabajo son: d_f(α) = 1,6390±0,1350 y d_f(β) = 1,5428 ±0,1727.

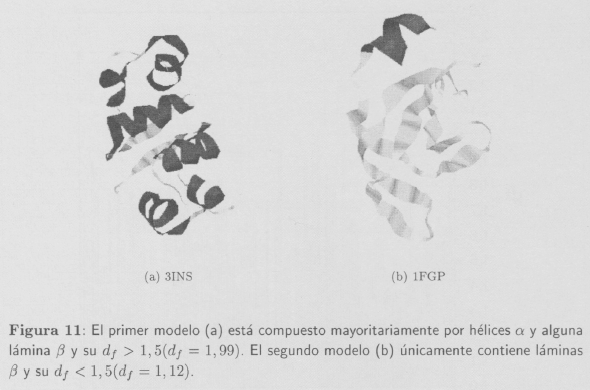
De los resultados estudiados se desprende que una primera interpretación del valor de la dimensión fractal debe tener relación con el grado de compactación de la estructura secundaria, y por tanto de la protema. En este sentido hemos demostrado que las estructuras más compactas, más densas (hélices α) presentan valores de la dimensión fractal más elevados que las estructuras menos densas, menos compactadas, como las estructuras β (ver Figura 11). La misma interpretación debe hacerse en el caso de considerar proteínas enteras, y no sólo partes de ellas. Es posible, por tanto, asignar un número que nos indica el grado de plegamiento de la cadena polipeptídica.

Puesto que el grado de irregularidad y de compactación de una proteína, de su superficie, debe estar relacionado con fenómenos como difusión, interacción con otras moléculas etc., los resultados presentados en este trabajo no deben ser considerados de forma aislada, sino que es necesaria su interrelación con otros aspectos relacionados con la funcionalidad de las proteínas. Se hace necesario por tanto, la realización de un estudio más completo y exhaustivo sobre la relación existente entre las dimensiones fractales encontradas y propiedades funcionales tales como plegamiento, interacción de ligandos con las proteínas, difusión, interacción de la proteínas con membranas, fármacos..., flexibilidad y vibración de las cadenas laterales de los aminoácidos, y cualquier otra propiedad que sea importante para la correcta funcionalidad biológica de las proteínas.

 

Referencias

[1] M. Daoud y J. E. Martin. Fractal properties of polymers. En D. Avnir, editor, The fractal approach to heterogeneous chemistry. Surface, Colloids, Polymers. John Wiley and Sons, New York, 1992.

[2] Fractint (freeware fractal generator). http://spanky.triumf.ca.        [ Links ]

[3] Li HQ, Li Y., y Zhao HM. Fractal analysis of protein chain conformation. Int. J. Biol Macromol, 12(1):6-8, 1990.

[4] Hyperchem™, 1993. Autodesk Inc.

[5] Y. Isogai y T. Itoh. Fractal analysis of tertiary structure of protein molecule. J. of the Physical Society of Japan, 53(6):2162-2171, 1984.

[6] B.B. Mandelbrot. The Fractal Geometry of Nature. W.H. Freeman and Co., 1982.        [ Links ]

[7] B.B. Mandelbrot. Los Objetos Fractales: forma, azar y dimensión. Ed. Tusquets, 1993.        [ Links ]

[8] Protein data bank (pdb). http://www.pdb.bnl.gov. Brookhaven, EUA.

[9] Pdbsum summaries and structural anlayses of pdb data files, http://www.biochem.ucl.ac.uk/bsm/pdbsum/.        [ Links ]

[10] H.O. Peitgen, H. Jürgens, y D. Saupe. Chaos and fractals: news frontiers of science. Ed. Springer-Verlag, 1982.        [ Links ]

[11] H.J. Stapleton. Fractal form of proteins. Physical Review Letters, 45:1456, 1980.        [ Links ]