https://doi.org/10.53287/qarh3525zj77f

A.ARTÍCULOS

 

Deprojection method and
arms structure of spiral
galaxies. Results for NGC
4939, NGC 5247 and NGC 157

 

Metodo de deproyección y estructura
de brazos de galaxias espirales.
Resultados para NGC 4939, NGC 5247
y NGC 157

 

 

Deterlino Urzagasti^1
1Carrera de Física, Universidad Mayor de San Andres, La Paz, Bolivia
durzagasti@fcpn.edu.bo
Recibido: 2 de julio de 2023     Aceptado: 28 de noviembre de 2023

 

 

---

Abstract

A numerical method is presented for the deprojection of disk images of normal spiral ga-laxies and for obtaining their arm structure using the logarithmic spiral model. The method is based on obtaining the points of local maxima and minima of the galactic image intensity fluctuations through a smoothing process with the Savitzky-Golay filter. These points then serve to determine the galactic disk inclination angles as well as the pitch angle of its spiral arms. The method is applied to three galaxies: NGC 4939, NGC 5247 and NGC 157, finding reasonable agreement with other results from the literature.

Subject headings: Galactic structure - numerical methods - image processing

---

Resumen

Se presenta un metodo numérico para la deproyección de imágenes de discos de galaxias espirales normales y para la obtencion de su estructura de brazos usando el modelo de espirales logarítmicas. El metodo se basa en la obtención de los puntos de máximos y mínimos locales de las fluctuaciones de la intensidad en las imagenes galácticas a través de un proceso de suavizado con el filtro de Savitzky-Golay. Estos puntos luego sirven para determinar los angulos de inclinación del disco galáctico así como el pitch angle de sus brazos espirales. El metodo se aplica a tres galaxias: NGC 4939, NGC 5247 y NGC 157, encontrándose un acuerdo razonable con otros resultados de la literatura.

Palabras clave: Estructura galactica - métodos numéricos - procesamiento de imágenes

---

 

 

1  Introduction

Before the application of analysis methods to the structure of galactic disks, it is essential the determination of its orientations with respect to some given coordinate system, or, in other words, its deprojection. Different methods are proposed for this effect, which are divided into two main groups: kinematic and photometric methods. In the former method, the only thing considered is the rotation of the galactic gas and its emission, thus determining an asymmetric velocity field that allows to determine the orientation angles under the assumption that the gas flows in a uniform circular motion and that the disk is an extremely thin system. Among the fotometric methods, the following are relevant: those based on Fourier analysis of galactic images, such as, for example, that of  García-Gómez et al., [2004], and those based on the application of least squares to the image points, which chosen with some suitable filter, correspond to the galactic arms; this is the case, for example, of the works of  Ma, [2001] and  Ma et al., [1999]. In general, the proposed methods allow also to determine the pitch angle, which is the angle between the tangent to an arm and the tangent te to a circunference that passes through the same pointand that is centered at the galactic center. This angle allows to characterize the curling degree of the arms and is strongly related to the galaxy morphological type (see e.g.  Ma et al., [1999]). Given its simplicity, the logarithmic spiral model is usually adopted to represent arms (see  Binney & Tremaine, [1987]). However, it is possible to obtain very reliable results without any imposition for the arms shape, as in the method described by  Poltorak & Fridman, [2007], where only a monotonous behavior is required.

In this work we develop an alternative method that consists of obtaining both the inclination angles of a galactic disk, assumed to be thin, and the pitch angle of its arms, assuming the logarithmic spiral model. The method is based in determining local maxima and minima of intensity fluctuations, with which, through an iterative adjustment process, it is possible to obtain the required parameters. Below we describe both the model and method used, and finally we apply the algorithm to three galaxies from the OSUBSGS (Ohio State University Bright Spiral Galaxy Survey).

 

2  Disk model

For the mass density in the galactic disk we use the following functional form:

where (r,Φ) are polar coordinates in the disk plane. In turn, for the arms structure the following model of logarithmic spirals is adopted:

where m is the number of arms and γ is a parameter of winding degree. However, in order to characterize the winding degree of spiral galaxies it is most useful the pitch angle, µ, which is related to the later parameters according to:

 

3  Logarithmic spirals

Curves called logarithmic spirals are obtained from the equality

and thus, the corresponding parametrization in the (x,y) plane is given by:

Hereinafter these curves will be called simply arms because they describe the different branches corresponding to different values of the constant in Equation (4).

In addition, the orthogonal curves to the arms have the following parametric representation:

Both families of curves are shown in Fig. 1a for q=1, whereas Fig. 1b shows the arms for different values of q. Note that the arms are more winded up for smaller values of q, that is, for smaller values of the pitch angle µ.

Fig. 1: (a) Arms (continuous red) and orthogonal (dashed blue) lines for q=1. (b) Arms for different values of q.

 

4  Grid construction

By using the families of curves described in the previous Section, an orthogonal curvilinear grid is constructed in order to have a better pixel position representation than those that are given by the other systems such as the cartesian and the polar ones. We call this grid as the spiral grid.

As a first step we adopt the criterion that the arc element length over an arm or over an orthogonal line be of the order of a pixel:

where p=1/q in the case of arms and p=−q in the case of orthogonal lines. This is a convenient choice because it is not possible to obtain more information on scales smaller than the width of a pixel. Given that according to Eqs. (5) and (6) we have ΔΦ = p Δr/r, the angular step corresponding to an arc on an orthogonal line (ΔΦ) is −q times the angular step corresponding to an arc on an arm (ΔΦ_b), that is

Moreover, when considering the variation of the angle Φ along an orthogonal line, we have that its minimum value is Φ_min=−q  ln r_max and its maximum value is Φ_max=−q  ln r_min, where r_max and r_min are the values of the maximum and minimum considered radius (in pixels units). If based on Eq. (7) we define r_min = Δr (1+q²)^−1/2 and also

then the number of segments of angular width ΔΦ on an orthogonal line, N=(Φ_max−Φ_min)/ΔΦ, is

The ends of these segments constitute sampling points throughout an orthogonal line; hence N is also the number of these points throughout the same line. r_max is measured from a center that is chosen from the position of the brightest pixel in the galactic center image. Finally, it remains to define the number of orthogonal lines in the array. Making use of Eq. (8), it is evident that this number can be defined as:

Typical values in this work are N ≈ N_o ≈ 500.

 

5  Grid Rotation

The plane of the galactic disc is rotated with respect to the plane of the sky (image plane) using Euler angles (θ_E,Φ_E,Ψ_E):

where (x’, y’) are cartesian coordinates in the disk plane and (x, y) are the corresponding coordinates in the image plane. Given the form of the parametric equations for the arms and their ortogonal lines, the rotation by Ψ_E can be directly introduced in the phase. Hence we can write:

where the factor n was added to give account of the sense in which the arms in the galactic image develop: n=1 (−1) if the arms develop clockwise (counter-clock wise). An example of a rotated spiral grid is shown in Fig. 2.

Fig. 2: Example of a rotated grid of logarithmic spirals. (Red continuous lines are arm lines and blue dashed lines correspond to orthogonal lines.) The rotation and degree of coiling were obtained for the NGC 4939 image.

 

6  Minimum radius

The studied images consist of uniform cartesian pixel arrays. Each pixel has assigned to a position and to a value of intensity. Since spiral grid does not have this uniformity, because the density of arms and orthogonal lines is greater towards the center, we must choose a minimum working radius to avoid the exaggerated repetition of intensity values, or, in other words, to avoid that a given pixel be used more than once by different arms and orthogonal lines. It is evident that this radius must be much greater to the previously chosen one, r_min , because this is used only to construct the spiral grid that must be rotated. In the following, the process of selection of this new minimal radius is described: First we make a mapping of intensity with the rotated spiral grid, that is, to each sampling point of the spiral grid the value of intensity corresponding to its position is assigned. The experience with the images that were used in this work indicates that a reasonable criterion to define the minimal radius, R_min, is that at this radius the number of contiguous points of equal intensity is equal to twenty times the number of contiguous points of different intensity. The count of these numbers of points is performed for all the orthogonal lines (i.e., for all the directions in the plane (x’, y’)). The number of sampling points in each of these lines is increasing towards the galactic center since ΔΦ = - q Δr/r, that is, ΔΦ > 0 for Δr < 0.

As an example, Figure 3a shows the count of the number of contiguous points for the image of NGC 4939. In this Figure, one sees that the number of points of different intensity is grater than the number of points of the same intensity (multiplied by a factor of twenty) for numbers of sampling points smaller than the corresponding to the intersection of the two curves (near 300). Moreover, the election of twenty factor is clearly justified in Fig. 3b, where for the same galaxy and for a typical orthogonal line, it is observed that for numbers of sampling points greater than 300, the repetition of intensity values originates a staggered structure towards the galactic center, which is not suitable for the filtering process to be described in the next Section. This is why the inner region to the minimal radius has been removed as shown in Fig. 2.

Fig. 3: (a) Total counts of the number of contiguous sampling point pairs along all orthogonal lines (401 lines) constructed for NGC 4939 as a function of the sampling point number along an orthogonal line, N_Φ, which is increasing toward the galactic center. The count is performed cumulatively from the galactic center. N_eq (N_ne) is the number of pairs of sampling points of equal (different) intensity. (b) Intensity plot for a typical orthogonal line of the same galaxy. The factor 20 is chosen so that the intersection of the two curves in (a), represented by the vertical line in (a) and (b), separates the inner galactic region where there are too many sampling points for the same pixel, or for the same pixel intensity, as seen in the step-like structure of the data to the right of the vertical line in (b).

 

7  Obtaining of the maxima and minima of the intensity fluctuations

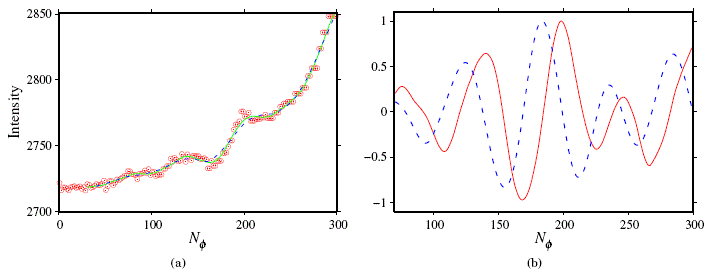
To obtain the maximum and minimum fluctuations in intensity, the intensity data is smoothed on each of the orthogonal lines of the spiral grid. To do this, the Savitsky-Golay filter is used ( Press et al., [1992]), which consists of fitting a polynomial function to a set of neighboring points close to a given point where you want to estimate the value of the function. This method then makes it possible to eliminate noise as well as the effect of sudden variations of the aforementioned function. In the present work, the filter is applied to the data set of intensity versus number of sampling points on each orthogonal line and two types of smoothing are introduced: the first, called coarse smoothing, with a number of neighbors N_g/2 to the left and N_g/2 to the right of each point on an orthogonal line; and the second, fine smoothing, with N_f/2 neighbors to the left and N_f/2 to the right of each sampling point. In both cases, the fitting polynomial is quadratic, following the suggestion of the implementation in  Press et al., [1992]. In turn, the choice of the number of neighbors arises from the experience of trying different numbers in the images used in this work. Figure 4a shows the application of this method to a typical orthogonal line of the galaxy NGC 4939.

Once the coarse and fine smoothing has been carried out, the corresponding resulting intensity values are subtracted to obtain the fluctuations in intensity. Then a fine smoothing is performed on these fluctuations and finally a fine smoothing with fourth degree polynomials is applied to the result of this last process to obtain the derivative of the fluctuations. The results are shown in Fig. 4b for the same orthogonal line as Fig. 4a. Here it should be noted that although fine smoothing of fluctuations is not necessary, it allows for better visualization of them.

With the aid of the obtained derivative, the points of local maxima and minima of the intensity fluctuations can be obtained. These points constitute the database for obtaining the degree of coiling of the arms and the Euler angles of a galaxy under study. However, it may happen that certain points in this set are spurious, that is, that the absolute value of the corresponding intensity fluctuation is not high enough. To correct this effect, those points whose absolute fluctuation is less than a certain lower limit δI_min are discarded. At the other extreme, there may be fluctuations with very high local values due to the presence of globular clusters or small satellite galaxies, for which the criterion of discarding from the set the points whose absolute fluctuations exceed the value of three times the root mean square deviation is chosen. Figure 5 shows the images of NGC 4939, NGC 5247 and NGC 157 and their corresponding maxima and minima of the intensity fluctuations found with the method above described.

Fig. 4: (a) Sampling points (circles) and the coarse (blue dashed line) and fine (green continuous line) smoothing on a typical orthogonal line of NGC 4939. (Graph of the Intensity as a function of the sampling point number along an orthogonal line, N_Φ, which is increasing toward the galactic center.) (b) Result of the difference between the fine smoothing and the coarse smoothing (continuous red curve normalized to its maximum value) of (a) and its corresponding derivative (dashed blue curve normalized to its maximum value).

 

Fig. 5: Images of the artificial galaxy No 6 of Table 1 (in terms of logarithm of the intensity), their maximum (upper panel) and minimum (lower panel) points, and the curves of the corresponding model adjustment (black lines). Also shown is the ellipse that comes from the projection of the galactic disk on the plane perpendicular to the line of sight, whose semi-major axis has an inclination with respect to the y axis (North Galactic Pole) equal to the position angle PA.

 

Fig. 6: Images of the galaxies under study (in terms of logarithm of the intensity), their maximum (upper panels) and minimum (lower panels) points, and the curves of the corresponding model adjustment (black lines). Also shown is the ellipse that comes from the projection of the galactic disk on the plane perpendicular to the line of sight, whose semi-major axis has an inclination with respect to the y axis (North Galactic Pole) equal to the position angle PA.

 

8  Obtaining of the winding degree

By using the parametric Eqs. (5), the curves that describe the maximum fluctuations of the intensity are given by:

where k indicates the number of arm of the galaxy under study. For the minimum intensity fluctuations we just have to write (2k+1) instead of 2k in the above equation. Therefore, for successive maxima or minima over the same orthogonal line, we have:

Hence, obtaining the N_q differences ΔΦ for all the successive minima and maxima over all the orthogonal lines, and then applying a simple statistics, the parameter q can be obtained.

 

Table 1: Parameters obtained through the application of the method (variables without superindex) to the artificial galaxy described in Section 10 for different values of the number of arms, the pitch angle and the orientation angles with respect to the plane of the sky (variables with superscript a). Euler angles are expressed in degrees.

 

9  Iterative procedure

For the calculations, a FORTRAN language program is used that is executed on a Linux platform. An iterative procedure is carried out starting with a non-rotated spiral grid and with a value q=1 for the degree of winding. During the first cycle of iterations, the Euler angles are estimated using the diagonalization method of a matrix similar to the inertia tensor used in mechanics for rigid bodies. In this case, the points of local maxima and minima of the intensity fluctuations play the role of particles of mass equal to the square root of the absolute value of the fluctuation in density: ¹. In any case, this first choice constitutes only a first approximation that is introduced in order to not manually enter the initial Euler angles. In subsequent cycles, the Euler angles are found by using a SIMPLEX ( Press et al., [1992]). The SIMPLEX used here is a geometric figure in a four-dimensional space that encloses the three angular parameters, the Euler angles. This changes its shape and reduces its volume until a certain function of the parameters reaches its minimum value within an established error tolerance order. The function chosen for this purpose is the root mean square deviation (σ) of the minimum distances between the maximum and minimum points and the sampling points on the arms of the model.

The steps followed in the iterations are roughly described below:

i. The spiral grid is generated.

ii. Savitzky-Golay filtering is applied to the dataset.

iii. Local maxima and minima of the intensity fluctuations are found.

iv. q parameter is calculated.

v. Euler angles are calculated using a SIMPLEX.

vi. A new spiral grid is generated and the entire process is repeated until convergence is achieved within the required error tolerance range in a number of N_iter iterations.

Once the iterative process is finished, the program returns the winding degree parameter and the three Euler angles. The error in the Euler angles is estimated by performing the subtraction between the values ​​obtained in the first and last applications of SIMPLEX (with a tolerance of 10⁻³ for σ). In this last iteration, the Euler angles reach a stable situation, no longer suffering significant changes with respect to the previous iteration. Note that in some cases one must modify the range of sampling points on the spiral arms of the model so that they cover all the points of maxima and minima. Experience with the actual galaxies studied in this work shows that the effect of this modification introduces a maximum error of the order of one degree.

 

10  APPLICATION TO NGC 4939, NGC 5247 AND NGC 157

Before applying the method to three galaxies from the OSUBSGS sample, we have applied it to an artificial galaxy with different pitch angles and different orientations with respect to the plane of the sky. This artificial galaxy (300x300 pixels) is built from the model given by Eq.  with log₁₀f₁(r)=3.6exp[−0.1log₁₀²r], and f₂(r)=20/r for r > 20 and f₂(r)=1 for r ≤ 20. The corresponding results for different numbers of arms, pitch angles, and orientation angles are shown in Table 1, where we can see that a good agreement is found between the parameters of the artificial galaxy and those obtained with our method. An example of the application of the method for parameter set No. 6 of this artificial galaxy is shown in Fig. 5.

The method is applied to the images of three galaxies from the OSUBSGS set and for the H filter: NGC 4939, NGC 5247 and NGC 157, which are shown in Fig. 5. The corresponding results are shown in Tables 1, 2 and 3 and in Fig. 6. In order to make the comparison with the results found in the literature for these three galaxies, the angles must be expressed in terms of the inclination angle IA and the position angle PA, as well as the degree of coiling in terms of the pitch angle, µ . In the present case:

Thus, IA is the angle between the axis of the galactic disk and the line of sight, and PA indicates the orientation of the line of the nodes of the projected disk and is the angle between this line and North, measured towards the East. Since the position angle PA is the angle between the north galactic pole (y axis in Fig. 6) and the major axis of the ellipse resulting from the projection of the galactic disk onto the plane of the sky, and since the intersection of this ellipse with that axis has two vertices, terms that are multiples of 180 degrees can be added to the position angle. For this reason we chose l to have a positive value less than 180 degrees for the position angle.

Table 2: Parameters obtained through the application of the method. Euler angles are expressed in degrees.

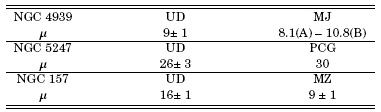
Table 3: Comparison between the values of IA and PA obtained in the present work (UD) and by  García-Gómez et al., [2004] (G-G) for NGC 4939, NGC 5247 and NGC 157. (Values expressed in degrees.)

 

Table 4: Comparison between the pitch angle values obtained in this work (UD) and by other authors:  Ma, [2001] (MJ),  Ma et al., [1999] (MZ), and  Patsis et al., [1991] (PCG). (Values expressed in degrees.)

 

11  Conclusions

The acceptable precision of the obtained results could indicate that the logarithmic spiral model is both simple and adequate to describe the arm structure of barless spiral galaxies, despite the approach that these are considered as flat objects.

However, a delicate aspect of the application of the model to galaxy image data is the process of obtaining the points of local maxima and minima of the local intensity fluctuations with which the degree of coiling and the orientation angles are obtained. The precision of the results is sensitive to the number of neighbors considered in the Savitzky-Golay filtering. Given the intrinsic irregularities of the images, smoothing is better for a relatively large number of neighbors, but this decreases the extent of the analysis region. At the other extreme, if the number of neighbors is relatively small, the extent of the analysis region is greater, but the dispersion in the positions of the maxima and minima is also greater. Additionally, in the later case, the appearance of modes with a greater number of arms is evident; but the limitation on the number of pixels in the images prevents obtaining precise results from them.

When comparing the results obtained for the orientation angles and pitch angle of the three galaxies studied with the values obtained by other authors, an acceptable agreement is found, indicating that the method developed in this work could be applied to a larger sample of spiral galaxies. However, there are large discrepancies with the results of other authors for the position angle of NGC 5247 and for the pitch angle of NGC 157. This indicates that a larger sample of galaxies must be taken to better test the algorithm (work in progress). Moreover, ideas arise to improve its efficiency that should be tested in the first instance. One of them is to use not only the maximum and minimum points of the fluctuations but also other nearby points and assigning a statistical weight to all the points considered, thus probably improving the sample and consequently the results. Another is to carry out a Fourier analysis of the intensity fluctuations obtained with the Savitzky-Golay smoothing along the lines perpendicular to the arms, in order to obtain the angular parameters through the corresponding spectra.

 

ACKNOWLEDGMENTS

This work has made use of data in fits format belonging to the Ohio State University Bright Spiral Galaxy Survey (OSUBSGS) project, which was funded by the budgets AST-9217716 and AST-9617006 of the United States National Science Foundation, with additional support from the Ohio State University. We thank this project and these institutions with the greatest consideration for allowing us to use these data.

Conflicts of interest The author declares no conflicts of interest with respect to the publication of this document.

 

Nota

¹ There is no qualitative explanation for this choice, as it arises from having carried out tests with different powers of | δI| so that both the inner and outer regions of the galactic image are represented in a more or less balanced way in the equivalent inertia tensor.

 

Reference

[Binney & Tremaine 1987]

Binney, J. & Tremaine, S. 1987, Galactic dynamics (Princeton University Press)        [ Links ]

[García-Gómez et al. 2004]

García-Gómez, C., Barberà, C., Athanassoula, E., Bosma, A., & Whyte, L. 2004, A&A, 421, 595        [ Links ]

[Ma 2001]

Ma, J. 2001, Chinese Journal of Astronomy and Astrophysics, 1, 395        [ Links ]

[Ma et al. 1999]

Ma, J., Zhao, J. L., Shu, C. G., & Peng, Q. H. 1999, A&A, 350, 31        [ Links ]

[Patsis et al. 1991]

Patsis, P. A., Contopoulos, G., & Grosbol, P. 1991, A&A, 243, 373         [ Links ]

[Poltorak & Fridman 2007]

Poltorak, S. G. & Fridman, A. M. 2007, Astron. Rep., 51, 460        [ Links ]

[Press et al. 1992]

Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd edn. (Cambridge University Press)        [ Links ]

[Río & Cepa 2003]

Río, M. S. d. & Cepa, J. 2003, A&A, 400, 421        [ Links ]

[Schlosser & Musculus 1984]

Schlosser, W. & Musculus, D. 1984, A&A, 131, 367        [ Links ]