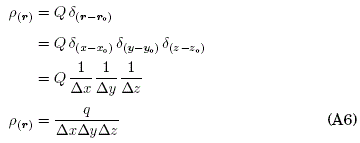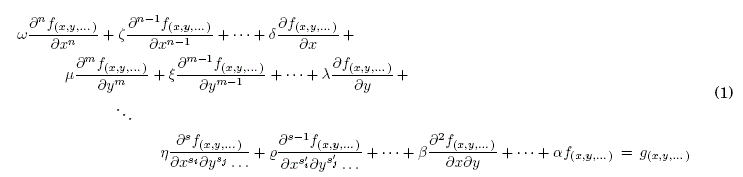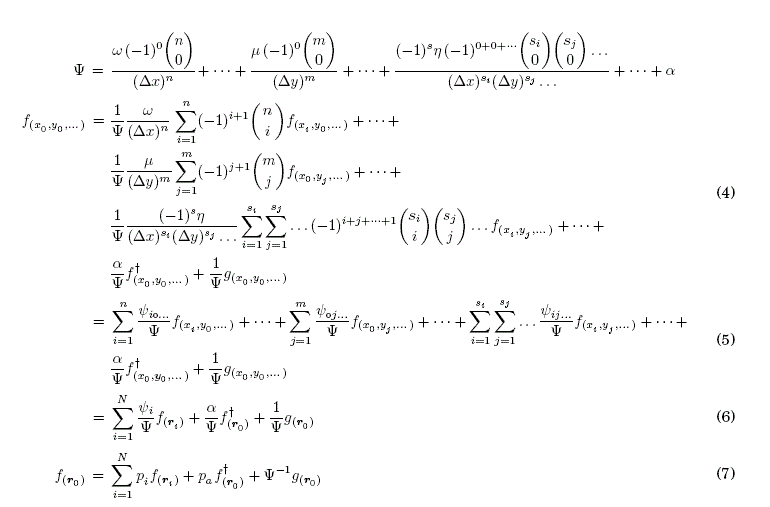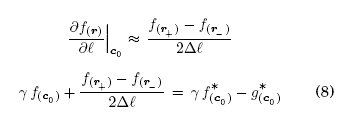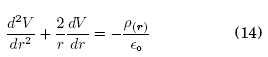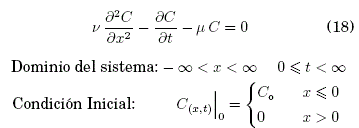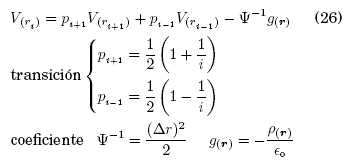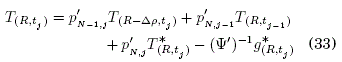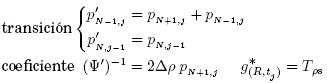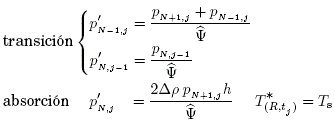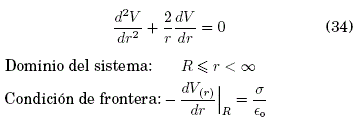https://doi.org/10.53287/zahz5450im22o

A.ARTÍCULOS

 

Solución de una EDP completa inhomogenea
e implementación de condiciones de frontera
mediante paseos aleatorios

 

An inhomogeneous complete pde solution
and the implementation of boundary conditions
through random walks

 

 

V. FRANZ SUXO MAMANI^†
Instituto de Física, Universidade de Sao Paulo,
Sao Paulo - Brasil
Recibido 4 de noviembre de 2022     Aceptado 12 de diciembre de 2022

 

 

---

Resumen

El término inhomogéneo de una Ecuación Diferencial Parcial (EDP), describe diferentes sistemas físicos que contienen fuentes o sumideros como: carga, materia o energía, mientras que el término que no posee derivada (término de orden cero) está relacionado con diversos procesos físicos como: enfriamiento de Newton, absorción de Lambert o desintegración radiactiva entre otros. Existen métodos estocásticos como paseos aleatorios para resolver EDP’s, por ejemplo,  Suxo, [2011] formuló un teorema aplicado exclusivamente a EDP’s homogéneas, sin tomar en cuenta el término de orden cero. Por tanto, a fin de ampliar el estudio a mayor cantidad de fenómenos físicos, en este trabajo reformulamos el teorema antes mencionado, tomando en cuenta el término de orden cero dentro una EDP inhomogénea. Adicionalmente, implementamos el estudio de las condiciones de frontera de Dirichlet, Neumann y Mixta. Finalmente, verificamos la eficacia del estudio confrontando los resultados obtenidos con soluciones analíticas de las ecuaciones de Poisson, Fick y Fourier.

Descriptores: EDP completa inhomogénea ­ Condiciones de Frontera ­ Paseo Aleatorio

---

Código(s) PACS: 02.30.Jr, 02.60.Lj, 05.40.Fb

---

Abstract

In a Partial Differential Equation (PDE), the inhomogeneous term describes different physical systems that contain sources or sinks such as: charge, matter or energy, while the term that does not have a derivative (zero order term) is related to diverse physical processes such as: Newton cooling, Lambert absorption or radioactive disintegration among others. There are stochastic methods such as random walks to solve equations, for example,  Suxo, [2011] formulated a theorem applied exclusively to homogeneous PDEs, without taking into account the zero order term. Therefore, in order to extend the study to several physical phenomena, in this work we reformulate that theorem taking into account the zero order term within an inhomogeneous PDE. In addition, we implement the study of the Dirichlet, Neumann and Mixed boundary conditions. Finally, we verify the effectiveness of the study by comparing the results obtained with analytical solutions of the Poisson, Fick and Fourier equations.

Subject headings: Inhomogeneous Complete PDE ­ Boundary Conditions ­ Random Walk

---

 

 

1  INTRODUCCIÓN

Fenómenos físicos por completo diferentes pueden describirse mediante un mismo modelo matemático o Ecuación Diferencial Parcial (EDP). Por ejemplo, una EDP parabólica modela procesos de evolución como difusión de materia o conducción de calor, entre tanto, una elíptica modela casos estacionarios como potenciales electrostáticos o membranas elásticas en reposo. Donde, la configuración inicial y la extensión espacial del sistema físico determinan la condición inicial y de frontera de la EDP respectivamente¹, es decir, el dominio del modelo matemático está definido en dimensiones espacio-tiempo. Por lo tanto, en el proceso de resolución de una EDP bajo un enfoque numérico, la condición inicial puede tratarse como una condición de frontera de tipo temporal.

A diferencia de la frontera espacial que puede ser cerrada o abierta, la frontera temporal en escencia es abierta porque está ubicada en el infinito, por tanto, la parte temporal del dominio es semi-infinita que abarca desde un instante inicial y se extiende hasta la eternidad (t_o≤ t < ∞). Sin embargo, como la frontera temporal no delimita el sistema físico de su entorno, el dominio temporal puede ser acotado de forma arbitraria sin alterar las propiedades del sistema. En contraste, el sistema y su entorno están en contacto en la frontera espacial, donde pueden ocurrir interacciones sistema-entorno a través de mecanismos conocidos como condiciones de frontera de Dirichlet, Neumann o una combinación de ambos denominada Mixta ( Arfken, [2007]). Por tanto, acotar un dominio espacial de carácter infinito significaría introducir ciertos errores de aproximación numérica en el proceso de resolución de una EDP.

Sistemas que obedecen la ley gravitacional o de naturaleza coulombiana están definidos sobre todo el espacio físico que es infinito, en consecuencia, si alguna propiedad del sistema es modelada a través de una EDP, la parte espacial del dominio adquiere dimensión infinita (0 ≤ r < ∞). En  Suxo, [2016], se encaran condiciones de frontera abiertas mediante paseos aleatorios, donde la estrategia para evitar paseos indeterminados es acotar el dominio espacial infinito, aunque en un dominio espacio-temporal no es necesario acotar porque el paseo siempre finaliza en la frontera temporal (condición inicial), mientras,  Doob, [1953] como estrategia predefine un número finito de pasos para interrumpir el paseo realizado sobre dominios infinitos. En suma, acotar el dominio o predefinir el número de pasos produce lo mismo, porque ambas estrategias finalizan/interrumpen el paseo aleatorio evitando procesos infinitos, es decir, la ampliación/reducción del acotamiento equivale a incrementar/disminuir los pasos predefinidos.

En una EDP, el término inhomogéneo representa diferentes aspectos físicos como presencia de cargas eléctricas en un medio dieléctrico, fuentes de calor en un material térmico o gradientes de presión en un fluido (líquido), donde los modelos matemáticos involucrados son las ecuaciones de Poisson, Fourier y Navier-Stokes respectivamente ( Kreyszig, [2006]). Por otro lado, el término sin derivar o término de orden cero está relacionado con diversos fenómenos físicos como: absorción de Lambert, enfriamiento de Newton, desintegración radiactiva, carga-descarga de capacitores o concentración iónica de disoluciones entre otros ( Simmons, [2002]), por ejemplo, el modelo matemático del último caso es la ecuación no-lineal de Poisson-Boltzmann que linealizada adquiere la forma de una ecuación modificada de Helmholtz.

Numéricamente, existen diferentes métodos para resolver una EDP inhomogénea que puede contener (o no) el término sin derivar, por ejemplo: Diferencias Finitas, Elementos Finitos o Redes de Boltzmann. Pero, como requieren de un montaje matricial en el proceso de resolución, son inaplicables a condiciones de frontera abiertas por la finitud matricial, a menos que, el dominio sea acotado (ver,  Sanjinés, [2006]). Estocásticamente, los métodos de resolución de una EDP están basados en probabilidades de transición, como: paseos aleatorios que abordan condiciones de frontera abiertas sin necesidad de un acotamiento (ver,  Suxo, [2016]). Además, en lugar de operaciones matriciales, requiere solamente cálculos aritméticos que son fáciles de programar, así como, en vez de una resolución global, puede ser posible una parcial que favorece el cómputo paralelo. Sin embargo, no hay antecedentes para resolver una EDP inhomogénea (u homogénea) que incluya el término sin derivar.

En este trabajo, se desarrolla una metodología basada en paseos aleatorios para resolver una EDP inhomogénea que integra el término sin derivar y que posee diversas condiciones de frontera: Dirichlet, Neumann o Mixta. Específicamente, se implementa el concepto de probabilidad de absorción dentro las probabilidades de transición de un paseo aleatorio, cuya implementación se efectúa reformulando el teorema desarrollado en  Suxo, [2011]. En síntesis, se generaliza el estudio realizado por  Suxo, [2011] para resolver EDP’s más complejas, pero conservando la simplicidad que ofrece la metodología estocástica.

 

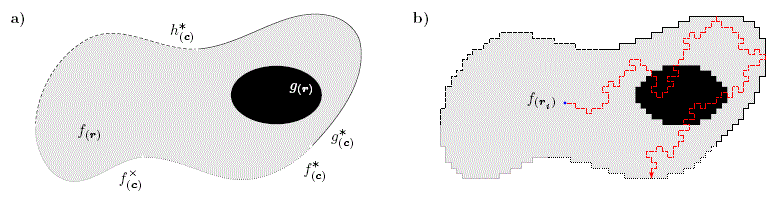
Figure 1: Representación gráfica de una EDP modeladora de un fenómeno físico. a) Esquema
del dominio Ω y frontera ∂Ω de una EDP. b) Paseo aleatorio de una partícula virtual realizado sobre el dominio
Ω y frontera ∂Ω de una EDP discretizada

 

2  METODOLOGÍA

Únicamente los fenómenos o sistemas físicos más sencillos pueden modelarse mediante EDO’s que dependen generalmente de una variable temporal, mientras que, la mayoría de los diversos tópicos avanzados de la Física Teórica son formulados en base a EDP’s que dependen de dos o más variables ( Kreyszig, [2006]). Entonces, una ecuación general que represente tanto a EDO’s como a EDP’s tiene la forma de la siguiente ecuación:

donde, f_(x,y,...) es la función incógnita que describe el sistema físico y g_(x,y,...) es una función conocida que es responsable de la inhomogeneidad del modelo matemático y representa a fuentes/sumideros, entre tanto, las letras griegas:  α, β, ..., ω  son coeficientes que en general dependen de las variables (x,y,...). Particularmente, si la EDP es homogénea pero con coeficientes constantes y la función f_(x,y,...) únicamente depende de dos variables con derivadas de segundo orden o menor, la EDP es lineal y puede ser reducida a una forma canónica: elíptica, parabólica o hiperbólica ( Arfken, [2007]).

Esquemáticamente, la función f_(x,y,...) ≡ f_(r) abarca todo el dominio del sistema (Ω), en cambio la función g_(x,y,...) ≡ g_(r) es un subdominio que puede cubrir todo, nada o parte del dominio (ver, Fig: 1a). Mientras que, la frontera del dominio denominada también borde o contorno (∂Ω), está conformada por funciones conocidas: f^×_(c), f*_(c), g*_(c) y h*_(c), donde, la primera función es la condición inicial relacionada con la frontera temporal (t = t_o) y las tres restantes se relacionan con la frontera espacial (r = r_c) que en específico son: la frontera de Dirichlet, Neumann y Mixta respectivamente (ver, Fig: 1a). Físicamente, las interacciones que ocurren en una interfaz sistema-entorno pueden ser tan diversas como complejas dependiendo del fenómeno físico, sin embargo, en general están conformadas por dos tipos de interacciones básicas, como ser:

Sistema f_(r) inmerso en un baño infinito f^*_(c) que emula idealmente el entorno.

Fuente/Sumidero g*_(c) de una magnitud física presente en la frontera del sistema.

donde, estas interacciones son las condiciones de frontera de Dirichlet y Neumann respectivamente.

Matemáticamente, las diferentes condiciones de frontera espacio-tiempo son expresadas como:

donde, h*_(c) = γf^*_(c) ­ g*_(c) es la suma o combinación lineal entre Dirichlet y Neumann con γ como factor dimensional. Puesto que, la frontera de Dirichlet e Inicial tienen la misma estructura matemática, en un análisis estocástico ambas expresiones tienen las mismas propiedades (es decir, f^×_(c) ≡ f^*_(c)).

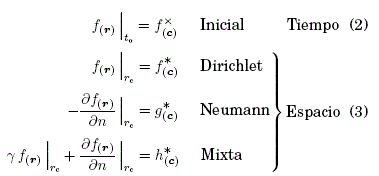
2.1  Reformulación del teorema

En  Suxo, [2011], la metodología para resolver una EDP está basada principalmente en paseos aleatorios y el objetivo principal es la formulación de un teorema sobre las probabilidades de transición obtenidas de la EDP discreta en diferencias finitas. Sin embargo, el teorema es exclusivo para una EDP (incompleta) conformada únicamente por términos que poseen derivadas igual o mayor a primer orden (n > 0), es decir, no se puede aplicar a una EDP (completa) como la Ec. (1) porque incluye el término de orden cero o sin derivar (n ≥ 0). Por lo tanto, para resolver una EDP completa es necesario reformular el teorema que fue desarrollado en  Suxo, [2011]. Un triángulo de Pascal conformado por elementos con signos alternados (+,­), puede ser construido a partir de los coeficientes de derivadas discretizadas en diferencias finitas centrales ( Sheid, [1968]), tal como se muestra a continuación:

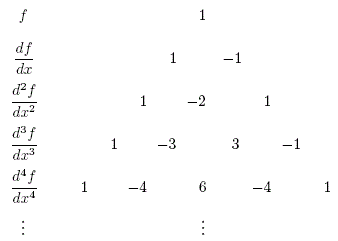
donde, la suma de coeficientes es igual a cero en cada derivada excepto en la derivada de orden cero o función sin derivar (primer renglón del triángulo). Según  Suxo, [2011], la sumatoria de coeficientes siempre es igual a cero independientemente si la derivada parcial n-ésima es regular o cruzada, así como también, no depende si la discretización en diferencias finitas es hacia adelante, atrás o central. Sin embargo, existen dos casos que pueden incluir el término sin derivar manteniendo la sumatoria de coeficientes igual a cero:

i) Si el coeficiente del término sin derivar αf_(x,y,...) es igual a cero (α = 0, ver Ec. (1)).

ii) Si existe una función conocida f^†_(x,y,...) que posee un coeficiente igual al término sin derivar pero de signo contrario, es decir: α[f_(x,y,...)­ f^†_(x,y,...)].

donde, evidentemente el primer caso es trivial, en cambio el segundo caso es complejo porque requiere de una función f^†_(x,y,...) que está relacionada con cierta probabilidad de absorción markoviana.

En el método de cadenas de Markov se construye una matriz con base en las probabilidades de transición de dos tipos de nodos: no-absorbente y absorbente localizados en dominio y frontera respectivamente, donde la frontera conformada por nodos absorbentes significaría una condición de frontera de Dirichlet ( Sadiku et al., [2002]). Desde la mirada de un paseo aleatorio, una partícula virtual se desplaza sobre el dominio realizando saltos aleatorios hacia los nodos más cercanos según determinadas probabilidades de transición y es absorbida si alcanza una frontera tipo Dirichlet, donde adquiere el valor de la función f*_(c) finalizando así su trayectoria (ver, Fig. 1b). En síntesis, la absorción en la frontera podría significar dos casos posibles: 0% de probabilidad de transición o 100% de probabilidad de absorción.

Por consiguiente, podemos explotar el concepto de probabilidad de absorción mencionado, pero aplicado sobre el dominio del sistema (Ω). Es decir, además de las probabilidades de transición hacia los nodos vecinos, existiría una probabilidad de absorción en el nodo presente finalizando así el paseo aleatorio antes de alcanzar la frontera del sistema (∂Ω), donde, la partícula virtual absorbida por el dominio adquiriría el valor de alguna función f^†_(r), equivalentemente como adquiere el valor de la función f^*_(c) cuando es absorbida por una frontera de Dirichlet. Por tanto, f^†_(r) y f*_(c) tendrían las mismas características y propiedades pero definidas en diferentes escenarios, el dominio y la frontera respectivamente.

A fin de reformular el teorema, adicionamos el término αf^†_(x,y,...) en el miembro inhomogéneo de la Ec. (1), posteriormente discretizamos las derivadas en diferencias finitas para obtener la Ec. (4) que es una EDP discreta desarrollada alrededor del punto (x₀,y₀,...), como se muestra a continuación:

donde, todos los términos sumatorios pueden ser expresados bajo una sola sumatoria (ver, Ec. (6)), porque cada uno de los términos sumatorios está relacionado a un determinado nodo vecino (r_i).

La Ec. (7) es la ecuación principal porque contiene toda la información para realizar paseos aleatorios, donde, el límite de la sumatoria N indica el número de nodos vecinos y los coeficientes i-ésimos p_i=Ψ_i/ψ son las probabilidades de transición. Mientras que, el coeficiente p_a= α/ψ es la probabilidad de absorción y complemento de las probabilidades de transición, es decir: p₁+p₂+...+p_N=1­p_a se cumple. Por tanto, el teorema formulado en  Suxo, [2011] puede ser reformulado y extendido de la siguiente manera:

Teorema. En la discretización en diferencias finitas de una ecuación diferencial parcial conformada por términos que poseen derivadas de orden cero o mayor, puede afirmarse que, el coeficiente de cualquier función es igual a la suma de los demás coeficientes pero de signo contrario. Entonces, si despejamos una función escogida al azar, los coeficientes resultantes de las demás funciones pueden ser tratables como probabilidades de transición-absorción.

Nota: El término inhomogéneo no forma parte del teorema, sin embargo es afectado por el coeficiente ψ^­1 que proviene de la discretización (ver, Ec. (7)).

 

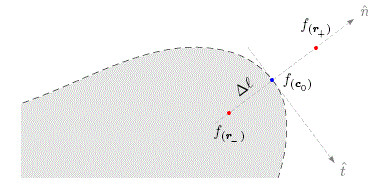
Figure 2: Representación esquemática de la discretización de una condición
de frontera espacial Mixta (ver, Ec. (8)).

 

2.2  Implementación de condiciones de frontera

Para poder aplicar el teorema reformulado sobre la frontera de un sistema (∂Ω), debemos discretizar en diferencias finitas sus condiciones de frontera. Entonces, como la condición de frontera espacial Mixta es una expresión general, discretizamos la última Ec. (3) de la siguiente manera:

donde, los puntos r₊ y r_­ son externos e internos al dominio respectivamente, entre tanto la coordenada l es normal a la frontera del dominio (ver, Fig. 2).

En procesos de transición-absorción en la frontera pueden ocurrir: transiciones tangenciales sobre la frontera, absorciones en la propia frontera o también reflexiones al interior del dominio (ver, Fig. 1b), pero está estrictamente prohibido saltos aleatorios desde la frontera hacia el exterior (entorno) del dominio (ver, Fig. 2). Por tanto, debemos y podemos eliminar la función f_(r+) combinando la Ec. (8) y la ecuación principal aplicada sobre la frontera (ver, Ec. (9)), como se muestra a continuación:

donde, la Ec. (13) tiene la misma estructura que la Ec. (7), también: p’₁+p’₂+...+p’_N­1=1­p’_a se cumple con (ψ’)^­1 como el coeficiente inhomogéneo. Si γ es extremadamente grande ()o prácticamente nulo (), la Ec. (13) describe una condición de frontera de Dirichlet o Neumann respectivamente.

2.3  Solución de una EDP completa inhomogénea

Para resolver estocásticamente una EDP como la Ec. (1) que puede estar conformada por diversas condiciones de frontera (ver, Ecs. (2)­(3)), aplicamos la Ec. (7) y Ec. (13) sobre el dominio y la frontera del sistema respectivamente. En específico, realizamos simulaciones computacionales de paseos aleatorios mediante partículas virtuales que evolucionan según dos conjuntos probabilísticos de transición-absorción diferentes: (p₁,p₂,...,p_N,p_a ) y (p’₁,p’₂,...,p’_N­1,p’_a) aplicados al dominio y frontera respectivamente. Una partícula absorbida por el dominio adquiere el valor f^†_(r), mientras que, si es absorbida por una frontera temporal (Condición Inicial) adquiere el valor f^×_(c), en cambio si es absorbida por una frontera espacial de Dirichlet adquiere el valor f*_(c). Además, si la partícula en su trayectoria atraviesa un subdominio adquiere el valor ψ^­1g_(r), pero si recorre una frontera de Neumann adquiere el valor (ψ’)^­1g*_(c). En una frontera Mixta, si la partícula es absorbida adquiere el valor f*_(c), en caso contrario, adquiere el valor (ψ’)^­1g^*_(c) y continúa el proceso.

En síntesis, la solución de un punto del dominio f_(ri) es igual al valor de absorción: f^†_(r), f^×_(c) o f*_(c) más el valor: ψ^­1g_(r) o (ψ’)^­1g^*_(c) si corresponde el caso (ver, Fig. 1b). Sin embargo, como el análisis es estocástico, la solución f_(ri) es aproximada al promedio de N simulaciones (paseos aleatorios) de partículas virtuales que emergen del punto r_i, donde cada simulación aleatoria finaliza en una absorción o cuando se ejecuta un número predefinido de pasos. Finalmente, la estimación de la solución f_(ri) tiene un error estadístico del orden ( Sobol, [1975]), es decir, si se obtienen mejores resultados.

 

3  APLICACIONES

Estudiamos diversos fenómenos físicos como ser: electrostática, transporte de materia y conducción de calor, específicamente, estudiamos el potencial eléctrico de cargas eléctricas (V), la concentración de una disolución (C) y la temperatura de un cuerpo (T), respectivamente. En cada fenómeno físico se estudian tres casos extremos y/o especiales.

3.1  Electrostática

El potencial eléctrico V_(r) existente en el espacio físico infinito es generado por la carga eléctrica total Q=4×10^­9 C que está distribuida en una esfera de radio R=6 cm. En coordenadas esféricas (ver, Fig. 3), el sistema tiene simetría polar y azimutal (θ ,Φ), por tanto, la función resultante es V=V_(r) y la ecuación de Poisson se expresa como:

Dominio del sistema: 0 ≤ r < ∞

donde, ε_o es la permitividad eléctrica del vacío y la función ρ_(r) ≡ ρ_(r,θ,Φ) es la densidad de carga.

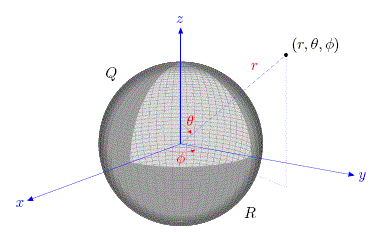
Figure 3: Representación esférica de un sistema de radio R con carga total Q
presente en el espacio infinito.

 

Según la configuración de cargas eléctricas sobre la esfera, estudiamos tres casos que tienen soluciones analíticas ( Wangsness, [1986]), como ser:

 

a) Esfera cargada:

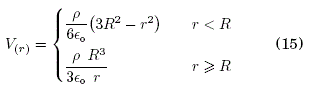
b) Esfera conductora: σ = Q/A  (A=4πR²)

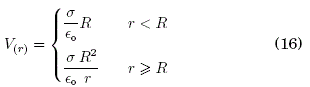
c) Monopolo eléctrico:

donde, ρ, σ y q son las densidades de carga eléctrica volumétrica, superficial y puntual respectivamente.

3.2  Transporte de materia

La difusión-reacción de la concentración C_(r) de una disolución de ClNa en un recipiente infinito es generado  por  una concentración de agua salada C_o=0.6 M más agua pura C_o=0.0 M inicialmente dividida. En coordenadas cartesianas (ver, Fig. 4), el sistema tiene simetría en profundidad y altitud (y , z), por tanto, la función resultante es C=C_(x,t) y la ecuación de Fick se expresa como:

donde,  v = 1,28 cm²/dia  y  µ = 0,05 dia^­1  son los coeficientes de difusión y reacción respectivamente.

 

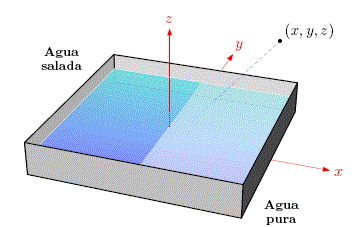
Figure 4: Representación cartesiana de una disolución de agua salada
y agua pura inicialmente dividida por el plano yz.

 

A partir de los valores v y µ, estudiamos tres casos extremos del sistema que tienen soluciones analíticas ( Spiegel, [1974]), como ser:

a) Proceso netamente difusivo:

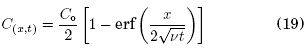
b) Proceso netamente reactivo:

c) Proceso difusivo reactivo: (v , µ > 0)

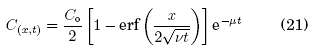
donde, erf(x) y sgn(x) son las funciones especiales error y signo respectivamente ( Spiegel et al., [2008]).

 

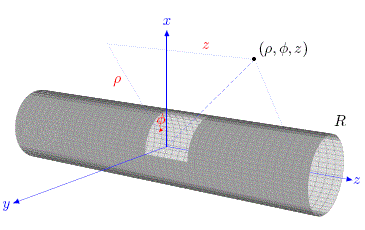
Figure 5: Representación cilíndrica de un sistema de longitud infinita y radio R expuesta al medio ambiente.

 

3.3  Conducción de calor

La difusión de temperatura T_(r) en un cilindro (metal Ag) de longitud infinita y radio R=10 cm es generado por su temperatura inicial T_o=0 ^°C y las diversas condiciones de frontera. a) Dirichlet: cilindro sumergido en un ambiente de temperatura T_s=6 ^°C, b) Neumann: gradiente de temperatura T_ρs=­1 ^°C/cm en la interfaz cilindro-ambiente y c) Mixta: proceso de enfriamiento de Newton sobre la interfaz en un caso semiaislado, T_ρs=0 ^°C/cm  y T_s=6 ^°C. En coordenadas cilíndricas (ver, Fig. 5), el sistema tiene simetría azimutal y longitudinal (Φ , z), por tanto, la función resultante es T=T_(ρ,t) y la ecuación de Fourier se expresa como:

donde, K = 1,75 cm²/s es el coeficiente térmico y como parámetro de enfriamiento el valor h=1,00 cm^­1. El sistema físico bajo estudio que es sometido a diferentes condiciones de frontera, tiene solución analítica en cada caso, como ser:

a) Frontera de Dirichlet ( Spiegel, [1974]):

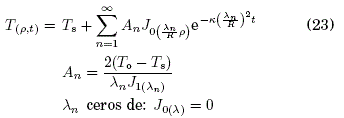
b) Frontera de Neumann ( Spiegel, [1965]):

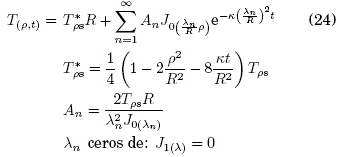
c) Frontera Mixta ( Spiegel, [1974]):

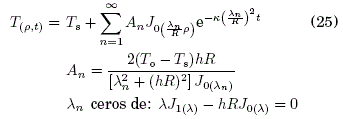
donde, J_0(x) y J_1(x) son funciones de Bessel de primera especie ( Spiegel et al., [2008]).

 

4  RESULTADOS

Con el objetivo de verificar la efectividad de la metodología desarrollada (ver, Sec. 2), resolvemos las ecuaciones de Poisson, Fick y Fourier a través de paseos aleatorios y comparamos los resultados obtenidos con sus soluciones analíticas (ver, Sec. 3). Para visualizar el error estimado de los resultados, seleccionamos problemas unidimensionales excepto en el caso del monopolo eléctrico (densidad puntual), donde realizamos un tratamiento tridimensional pero presentamos resultados unidimensionalmente.

4.1  Ecuación de Poisson

La Ec. (14) es una EDP incompleta e inhomogénea porque no existe un término sin derivar y su término inhomogéneo es diferente de cero², además, sólo posee una condición de frontera espacial que se ubica en el infinito . Entonces, la discretización de la Ec. (14) a través de diferencias finitas genera la siguiente ecuación principal:

Dominio del sistema:

donde, las probabilidades de transición dependen de la posición ’ i ’ y no existe probabilidad de absorción. Dado que la Ec. (26) está sujeta a la función g_(r), discretizamos las diversas densidades de carga ρ_(r) (ver, Ape. A) que se presentan a continuación:

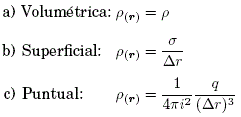
donde, a) y b) son constantes, mientras c) es función de la posición ’ i ’ e indeterminado en el origen (i=0). El potencial eléctrico V=V_(r) generado por una esfera cargada de densidad uniforme ρ o una esfera conductora de densidad superficial σ, se presentan en la Fig. 6a y Fig. 6b respectivamente. Sin embargo, el monopolo eléctrico no es viable bajo coordenadas esféricas (o cilíndricas) porque la ubicación de una carga puntual en el origen produce indeterminación. Por tanto, abordamos el problema bajo coordenadas cartesianas pero tridimensionalmente porque no hay simetría sobre los ejes, es decir la EDP es:

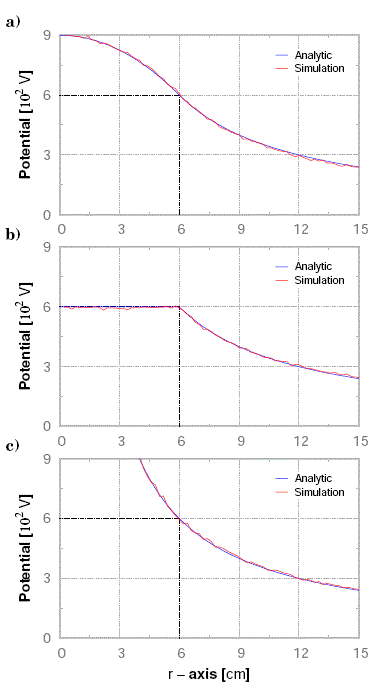
Figure 6: Resultados de una Ecuación de Poisson (ver, Ec. (14)).
a) Esfera cargada, b) Esfera conductora y c) Monopolo eléctrico.

 

El potencial eléctrico V = V_(x,y,z) generado por un monopolo eléctrico de carga q se expone en la Fig. 6c , pues, la Ec. (27) en diferencias finitas es la siguiente ecuación principal:

Dominio del sistema:

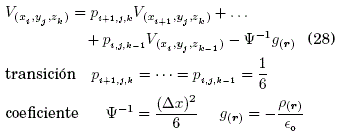
donde, si Δx=Δy=Δz se generan probabilidades de transición de valor igual, así como una densidad de carga ρ_(r)=q/(Δx)³ constante (ver, Ape. A).

 

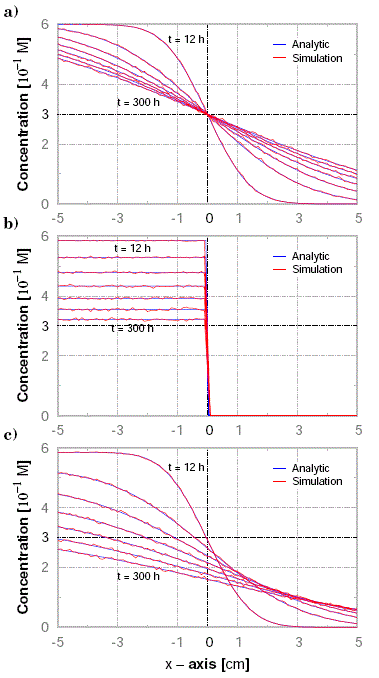
Figure 7: Resultados de una Ecuación de Fick (ver, Ec. (18)). Proceso: a) Difusión, b) Reacción y c) Difusión-Reacción.

 

4.2  Ecuación de Fick

La Ec. (18) es una EDP completa y homogénea porque existe un término sin derivar y su término inhomogéneo es igual a cero³, además, posee una condición inicial (t=0) y condiciones de frontera que se ubican en el infinito . Entonces, la Ec. (18) discretizada mediante diferencias finitas genera la siguiente ecuación principal:

Dominio del sistema:

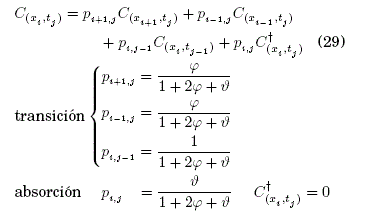
Condición inicial:

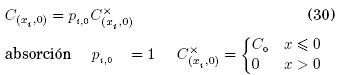
donde, son adimensionales y las probabilidades transición-absorción constantes. La concentación C=C_(x,t) de ClNa en un proceso difusivo ó reactivo , se presentan en la Fig. 7a y Fig. 7b respectivamente, mientras que, el proceso de difusión-reacción se presenta en la Fig. 7c. En cada caso, calculamos siete instantes de tiempo en intervalos de 48 h, desde t=12 h hasta t=300 h.

4.3  Ecuación de Fourier

La Ec. (22) es una EDP incompleta y homogénea porque no existe un término sin derivar y su término inhomogéneo es igual a cero, además, posee una condición inicial (t=0) y diversas condiciones de frontera aplicadas sobre el área lateral del cilindro (ρ = R). Entonces, la Ec. (22) discreta en diferencias finitas genera la siguiente ecuación principal:

Dominio del sistema:

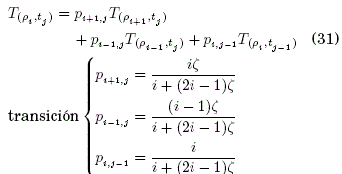
Condición inicial:

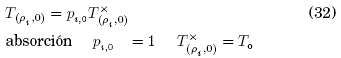
Condiciones de frontera:

donde, R = NΔρ y es adimensional, las probabilidades de transición varían según ’ i ’ y no existe una probabilidad de absorción en el dominio. La Ec. (33) expresa las condiciones de frontera de forma general y según el parámetro físico h ( ≡ γ) describe una frontera de Dirichlet, Neumann o Mixta (ver,  Sec. 2.2 y Ec. (13)), como muestra lo siguiente:

a) Frontera de Dirichlet:

b) Frontera de Neumann:

c) Frontera Mixta: (h > 0)

donde, h en caso Mixto (ver, Ec. (12)). La temperatura T=T_(ρ,t) del cilindro metálico (Ag) sometido a una temperatura exterior T_s ó a un gradiente de temperatura T_ρs sobre su superficie, se presentan en la Fig. 8a y Fig. 8b respectivamente, mientras que, el cilindro sometido a un proceso de enfriamiento de Newton se presenta en la Fig. 8c. En cada caso, calculamos siete instantes de tiempo en intervalos de 1,2 s, desde t=0,7 s hasta t=9,1 s.

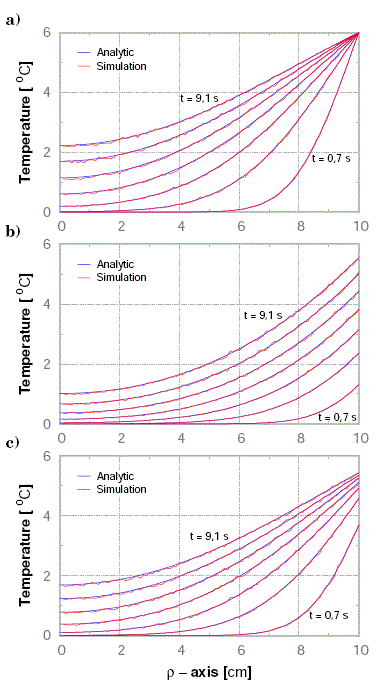
Figure 8: Resultados de una Ecuación de Fourier (ver, Ec. (22)). Condición de Frontera: a) Dirichlet, b) Neumann y c) Mixta.

4.4  Bonus - Track

Resolvemos el exterior de una esfera conductora (ver, Sec. 3.1), pero vía Ecuación de Laplace que posee condición de contorno tipo Neumann, es decir:

entonces, la Ec. (34) discreta en diferencias finitas genera la siguiente ecuación principal:

Dominio del sistema:

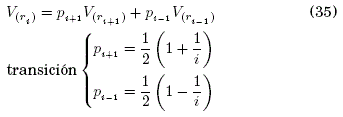
Condición de frontera:

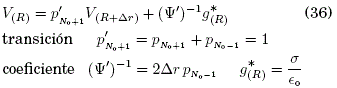
donde, N_o es referido al contorno esférico (R = N_oΔr).

El resultado de la Ec. (34) es igual al resultado de la Ec. (14) para valores r ≥ R (ver, Fig. 6b), es decir la inhomogeneidad de la Ecuación de Poisson equivale a la frontera de Neumann de la Ecuación de Laplace.

 

5  Conclusiones

La reformulación del teorema permite resolver una EDP inhomogénea que puede estar conformada por términos de cualquier orden de derivada incluido el término de orden cero (o sin derivar), así como también puede poseer diversos tipos de condiciones de frontera. En especial, implementar el concepto probabilidad de absorción dentro las probabilidades de transición de un paseo aleatorio es el principal aporte del trabajo, porque permite abordar procesos reactivos y el enfriamiento de Newton que suceden en el dominio y la frontera respectivamente.

 

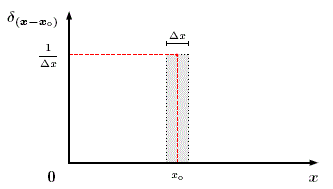
Figure 9: Esquema de una función delta de Dirac discretizada. El área es igual
a 1 y la función δ_(x­xo) es infinita en x_o si

 

Conflicto de intereses

El autor declara que no hay conflicto de intereses respecto a la publicación de este documento.

 

Notas

¹ Un sistema físico que posee únicamente condiciones iniciales es modelado mediante una Ecuación Diferencial Ordinaria (EDO).

² Si ρ_(r) = 0 significa ausencia de cargas, entonces la Ec. (14) se transforma en homogénea denominada Ecuación de Laplace.

³ Si µ = 0 significa que el término sin derivar es descartado, entonces la Ec. (18) se transforma en una EDP incompleta.

 

References

[Arfken 2007]

Arfken, W. 2007, Métodos matemáticos para físicos (U.S.A.: Diana)         [ Links ]

[Doob 1953]

Doob, J. L. 1953, Stochastic Processes (John Wiley & Sons, New York) Links ] Arial, Helvetica, sans-serif">

[Jackson 1999]

Jackson, J. D. 1999, Classical electrodynamics, 3rd edn. (New York, NY: Wiley) Links ] Arial, Helvetica, sans-serif">

[Kreyszig 2006]

Kreyszig, E. 2006, Advanced Engineering Mathematics (John Wiley & Sons) Links ] Arial, Helvetica, sans-serif">

[Sadiku et al. 2002]

Sadiku, M. N., Gu, K., & Obiozor, C. N. 2002, International Journal of Engineering Education, 18, 745 Links ] Arial, Helvetica, sans-serif">

[Sanjinés 2006]

Sanjinés, D. 2006, Revista Boliviana de Física, 12, 17 Links ] Arial, Helvetica, sans-serif">

[Sheid 1968]

Sheid, F. 1968, Numerical Analysis (McGraw-Hill) Links ] Arial, Helvetica, sans-serif">

[Simmons 2002]

Simmons, G. 2002, Differential Equations with Applications and Historical Notes (U.S.A.: McGraw-Hill) Links ] Arial, Helvetica, sans-serif">

[Sobol 1975]

Sobol, I. M. 1975, The Monte Carlo Method (Mir Publishers) Links ] Arial, Helvetica, sans-serif">

[Spiegel 1965]

Spiegel, M. 1965, Schaum’s Outline of Laplace Transforms, Schaum’s Outlines of Theory and Problems (McGraw-Hill Education)

[Spiegel 1974]

-. 1974, Schaum’s Outline of Fourier Analysis with Applications to Boundary Value Problems, Schaum’s Outline Series (McGraw Hill LLC)

[Spiegel et al. 2008]

Spiegel, M., Lipschutz, S., & Liu, J. 2008, Schaum’s Outline of Mathematical Handbook of Formulas and Tables, 3ed, Schaum’s Outline Series (McGraw-Hill Education)

[Suxo 2011]

Suxo, F. 2011, Revista Boliviana de Física, 19, 24 Links ] Arial, Helvetica, sans-serif">

[Suxo 2016]

-. 2016, Revista Boliviana de Física, 29, 1

[Wangsness 1986]

Wangsness, R. K. 1986, Electromagnetic fields / Roald K. Wangsness., 2nd edn. (New York: Wiley)         [ Links ]

 

APÉNDICE

A  DISCRETIZACIÓN DE LA FUNCIÓN

Unidimensionalmente, la definición de una función delta de Dirac discreta es la siguiente:

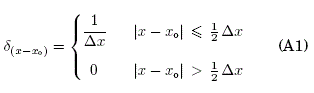
donde, δ_(x­xo) guarda sus propiedades (ver, Fig. 9). En electromagnetismo, la distribución o función densidad de cargas eléctricas ρ_(r) está representada por una función delta de Dirac ( Jackson, [1999]), como se muestra a continuación:

donde, Q es la carga y δ_(r­ro) tiene dimensión [l ^­3].

Esfera cargada

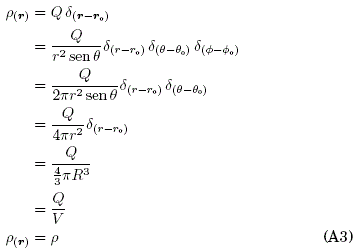
Esfera conductora (r,θ,Φ): σ = Q/A  (A=4πR²)

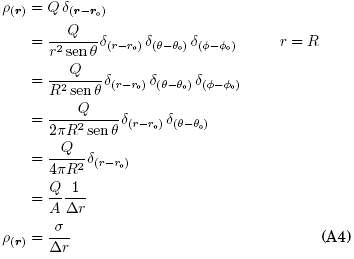
Monopolo eléctrico

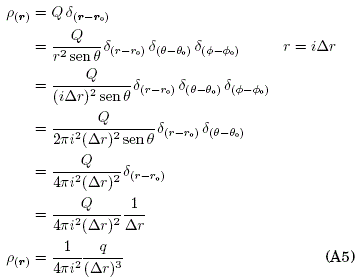
Monopolo eléctrico (x,y,z): q=Q