A. ARTÍCULOS

 

Acoplamiento de la electrodinamica de
Maxwell-Chern-Simons a un campo gravitacional
en presencia de un medio optico no dispersivo en
2+1 dimensiones

 

Coupling of the Maxwell-Chern-Simons electrodynamics with a
gravitational field in the presence of a non-dispersive optical
medium in 2+1 dimensions

 

 

Mirko Landivar^*
*Instituto de Investigaciones Fısicas, Universidad Mayor de San Andrés Campus Universitario,
c. 27 Cota-Cota, Casilla de Correos 8635 La Paz - Bolivia
mlandivarg@fcpn.edu.bo
Recibido 22 de septiembre de 2021      Aceptado 12 de noviembre de 2021

 

 

---

Resumen

e1em Se estudia la teoría de Maxwell-Chern-Simons con un acoplamiento con un campo gravitacional en el vacío y en presencia de un medio óptico simple que permea una región consi-derablemente grande del espacio, a través de la introducción de la métrica óptica de Gordon. Se escribe la acción de la teoría en un espacio-tiempo general, se obtienen las ecuaciones de campo, y se hallan generalizaciones de la ecuación de Klein-Gordon para cada caso. Luego se exploran los casos de espacio-tiempos maximalmente simétricos, donde se obtienen ecuaciones de onda masiva para el tensor de campo electromagnético. Un resultado peculiar es que en los espacio-tiempos de de Sitter en presencia de un medio óptico, la parte eléctrica del tensor de campo exhibe una masa diferente de la masa de la parte magnética.

Descriptores: Teoría clásica de campos - Electromagnetismo clásico, ecuacionés de Maxwell - Otras teorías clásicas especiales de campo.

---

Código(s) PACS: 03.50.-z - 03.50.De - 03.50.Kk

---

Abstract

We study the Maxwell-Chern-Simons theory coupling it to a gravitational field in a va-cuum and under the presence of a simple optical medium that permeates a considerably large region of space, by means of the introduction of the Gordon optical metric. We describe the action of the theory, derive the field equations, and obtain generalizations of the Klein-Gordon equation for each case. Then we explore the cases of maximally symmetric space time, where we obtain massive wave equations for the electromagnetic field tensor. A particularly interesting result is that in the de Sitter family of space time, under the presence of the optical medium, the electric part of the field tensor has a mass greater than the mass of the magnetic part.

Subject headings: Classical field theory - Classical electromagnetism, Maxwell equations - Other special classical field theories.

---

 

 

1.Introducción

La electrodinámica clásica, descrita por las ecuaciones de Maxwell, puede generalizarse al caso de un espacio-tiempo curvo al aplicarse una prescripción de acoplamiento mínimo (Misner et al , [2017]). Las ecuaciones de campo pueden obtenerse a partir de un principio variacional aplicado a la acción

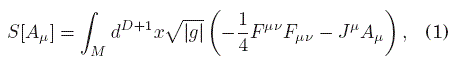
resultando en las ecuaciones de Maxwell inhomogéneas,

donde F_μν=∇_μ A_ν−∇_ν A_μ=∂_μ A_ν−∂_ν A_μ es el tensor de campo, definido a partir de la 1-forma A=A_α dx^α ∈ T^*M, la cual puede verse como una sección del haz de fibras cotangente de la variedad espacio-temporal M, g es el tensor métrico de signatura (+,−,...,−) que estará determinado por las ecuaciones de campo de Einstein, aunque más adelante supondremos que está dado, y que la presencia del campo eléctrico no perturba significativamente al campo gravitacional; y J es el vector de densidad de corriente asociado a posibles fuentes del campo electromagnético. Por otro lado, de la definición de F, se tiene la siguiente identidad

que recibe el nombre de identidad de Bianchi de la teoría, y reproduce las ecuaciones de Maxwell inhomogéneas. Esta identidad puede escribirse igualmente reemplazando las derivadas covariantes por derivadas parciales, debido a la propiedad de simetría de la conexión de Christoffel con que se ha equipado a la variedad diferencial M, y la antisimetría del tensor de campo.

Sin embargo, la acción (1) es sólo una de las muchas posibilidades de combinar al campo A y derivadas de sus componentes en una forma invariante bajo transformaciones generales de coordenadas y bajo transformaciones de calibre. Por ejemplo, uno podría introducir cualquier término con funciones de la forma f(F^μνF_μν), y seguiría conservando la invariancia frente a transformaciones ge-nerales de coordenadas y frente a transformaciones de calibre. Entonces, uno debe buscar alguna motivación extra para introducir términos a la acción y obtener variantes de la teoría.

Una motivación interesante, al menos desde el punto de vista matemático, es la de tener términos que al integrarse en la acción resulten en invariantes topológicos, y se les suele llamar términos topológicos. Estos términos no dependen explícitamente de la métrica de fondo, de modo que homeomorfismos aplicados a la variedad de espacio-tiempo, a nivel de su estructura topológica solamente, dejan invariantes a estos términos. O, en otras palabras, basta que el mapa de transformación sea un homeomorfismo entre espacios topológicos para dejar invariantes a estos términos, y no se necesita un requerimiento mayor en el mapa de transformacion, sólo exigencias a nivel de la topología de la variedad.

Un ejemplo de corrección a la acción mediante un término topológico fue dada por Deser et al. , [1982] introduciendo en la acción un término de Chern-Simons, escribiendo la siguiente lagrangiana para el caso de un campo de calibre abeliano

donde consideraron un espacio-tiempo plano de 2+1 dimensiones. Asimismo, hallaron que esta teoría des-cribe fotones masivos, debido a que el tensor campo F_μν obedece a una ecuación de Klein-Gordon

donde \square = ∂^α∂_α es el d'Alembertiano. La relación de dispersión asociada a (5) es η_μνk^μk^ν = λ², de donde se interpreta que el valor absoluto de la constante de acoplamiento λ de Chern-Simons es la masa del campo electromagnético. Podemos decir entonces que el término topológico dota de masa al campo. Otra característica importante de los términos topológicos es que, al no depender de la métrica de fondo, no contribuyen al tensor de energía-momento total que es fuente del campo gravitacional a través de las ecuaciones de Einstein. Debe mencionarse también que una motivación fenomenológica para el estudio de teorías de calibre en 2+1 dimensiones puede encontrarse en su conexión con el comportamiento a altas temperaturas de modelos en 3+1 dimensiones (ver, por ejemplo, Weinberg , [1978])

En este trabajo pretendemos generalizar la ecuación (5) al caso de la presencia de un campo gravitacional general, y estudiar el caso particular de un espacio-tiempo de la familia de de Sitter, el cual involucra la constante cosmológica Λ. Asimismo, también se estudiará, sobre un espacio-tiempo ge-neral, esta misma electrodinámica en presencia de un medio óptico simple (i.e.: localmente homogéneo, isotrópico y lineal), empleando la llamada métrica óptica, introducida por Gordon , [1923], la cual es útil en la formulación covariante de la electrodinámica en medios, llamada electrodinámica de Minkowski (véase, por ejemplo, Novello y Bittencourt , [2012]). Se acoplará el término de Chern-Simons a la métrica óptica mediante contracciones, dejando el carácter de invariante topológico de este término sólo como un límite, pero preservando la invariancia de calibre.

Este artículo está organizado como sigue: en la sección 2 mostraremos el acoplamiento de la lagrangiana (4) a un campo gravitacional, y mostraremos la generalzación de la ecuación (5), luego supondremos que el espacio-tiempo es maxi-malmente simétrico (i.e. algún espacio tiempo de la familia de de Sitter o el espacio-tiempo de Minkowski), y veremos los efectos del campo gravitacional sobre la masa del campo electromagnético mediante la generalización de la ecuación de Klein-Gordon. Luego, en la sección 3, introduciremos la presencia de un medio simple, y buscaremos una nueva generalización de la ecuación de Klein-Gordon en el espacio-tiempo maximalmente simétrico, obteniendo nuevos efectos sobre la masa de las componentes eléctrica y magnética del tensor F. En particular, encontraremos que las masas del campo eléctrico y magnético son diferentes. Exploraremos valores críticos de las masas de los campos en función del valor de la constante de acomplamiento de Chern-Simons y de la constante cosmológica. Finalmente, damos algunas conclusiones, comentarios y perspectivas.

 

2.  Acomplamiento con un campo gravitacional

La aplicación de la prescripción de acoplamiento mínimo a la lagrangiana de Maxwell-Chern-Simons (4) resulta en la acción

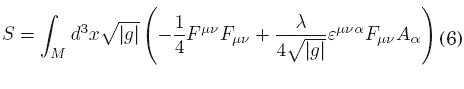
Aquí, es evidente que el término de CS es un invariante topológico debido a que el jacobiano se cancela, y no hay dependencia explícita de la métrica. Note que la invariancia bajo transformaciones ge-nerales de coordenadas queda asegurada debido a que son las componentes de un tensor auténtico, a pesar de la apariencia, dado que ε^μνα es el símbolo de Levi-Civita, que es una densidad tensorial de primer orden. Las componentes del anterior tensor con índices bajos son

Las ecuaciones de Euler-Lagrange resultantes son

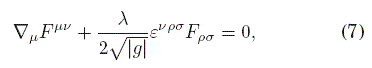
y la identidad de Bianchi (3) aun vale porque solo depende de la forma de la definición de F.

Si aplicamos ∇^α a la identidad de Bianchi (3), tenemos

donde hemos usado la condición de metricidad ∇_αg_μν= 0 y la antisimetría de F. Ahora, las derivadas covariantes en general no conmutan, sino que

Donde R^α_σαν es el tensor de curvatura de Riemann. Además usando la identidad

la ecuación (8) se escribe

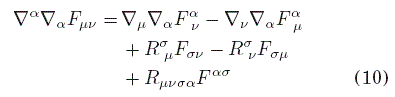
donde R^σ_μ es el tensor de Ricci. Ahora, de la ecuación de campo (8),

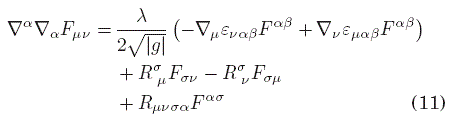
Aquí es conveniente definir el dual del tensor de campo como , de donde también es posible escribir . Multiplicando a la ecuación (7) por ε_ναβ, se obtiene

Luego, al introducir (12) en (11) el resultado es

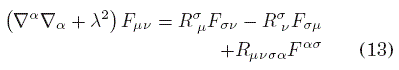
de donde vemos que, para un espacio tiempo plano, se recupera la ecuación (5). Evidentemente, la ecuación (13) es la generalización de la ecuación de Klein-Gordon que Deser et al. , [1982] hallaron en su trabajo.

2.1 En un espacio maximalmente simétrico

Se sabe que para un espacio-tiempo de dimensión D+1 de simetría máxima (i.e. uno que tiene (D+2)(D+1)/2 vectores Killing independientes, que son los generadores de isometrías, es decir, difeomor-misfos que preservan la métrica), la cuvatura escalar es una constante. Solo hay tres espacio-tiempos de esa naturaleza: El espacio-tiempo de Minkowski, con curvatura escalar nula, y las dos familias de espacio-tiempos de de Sitter, uno con R > 0 (de Sitter) y el otro con R < 0 (anti de Sitter). Tomemos el caso de algún espacio-tiempo de la familia de de Sitter en 2+1 dimensiones, en el cual el tensor de curvatura Riemann se escribe (véase Misner et al , [2017])

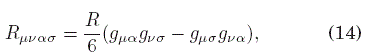
de donde resulta que el tensor de Ricci es

con lo que, de la ecuación de campo de Einstein con constante cosmológica

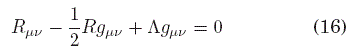
se tiene que la curvatura escalar es R = 6Λ.

La métrica puede escribirse en cierto sistema de coordenadas (t,r,Φ) mediante el elemento de línea

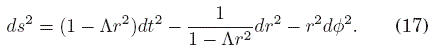
Con los resultados de las ecuaciones (14) y (15), y la curvatura escalar en términos de la constante cosmológica, la ecuación (13) se reduce a

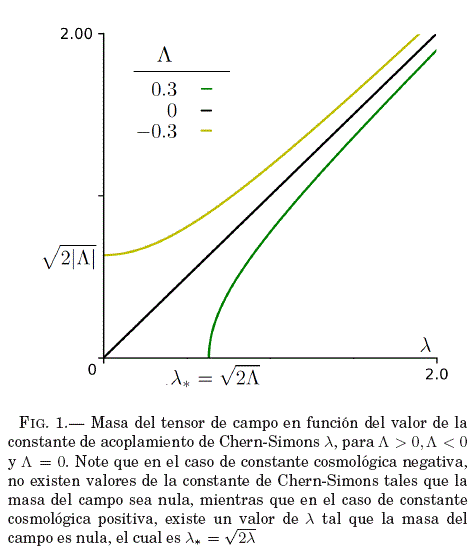
de donde es manifiesto el efecto de la constante cosmológica sobre la masa del campo electromagnético en esta teoría, siempre que λ²≥ 2Λ. La masa del campo entonces está dada por . En la figura 1 se muestra la dependencia de la masa con la constante de acoplamiento de Chern-Simons para valores representativos de la constante cosmológica.

Para el caso particular en que λ²=2Λ, tenemos que la ecuacion (18) se reduce a una ecuación de onda sin masa,

Desde el punto de vista dinámico para este caso, donde en algún sistema de coordenadas se elige x⁰=t como la coordenadas temporal y xⁱ como las coordenadas temporales, la ecuación (19) tendrá soluciones de onda en este espacio-tiempo con la restricción de que los perfiles iniciales sean soluciones del problema

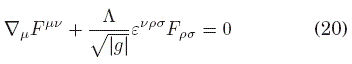
con ν = 0, que sería el análogo a la Ley de Gauss, más la identidad de Bianchi con índices espaciales, que sería la Ley de Gauss para el campo magnético; todo esto con condiciones de frontera apropiadas.

 

3 Presencia de un medio simple

Supongamos que en cierta región de un espacio-tiempo plano de D+1 dimensiones existe un medio óptico simple, es decir, localmente homogéneo, isotrópico y lineal. ¿Cómo se describe la electrodinámica en una forma manifiestamente covariante? La respuesta está en la introducción de la métrica de Gordon , [1923] (véase también Thompson , [2018]), que se define por

donde η es la métrica de Minkowski, κ es una constante que depende de los parámetros ópticos del medio en la forma κ = εμ−1, y u_μ es la 3-velocidad del medio, de modo que en el sistema de referencia inercial en reposo respecto del medio, las componentes de u son u_μ = (1,0,...,0). Definimos entonces la acción del campo electromagnético en presencia de un medio simple (en un espacio-tiempo plano)

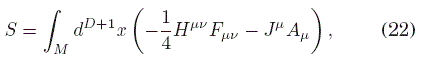
donde se definió al tensor auxiliar

que es análogo a los campos vectoriales auxiliares D y H de la electrodinámica en medios en 3+1 dimensiones. Note el uso de la métrica óptica en esta definición. Por otro lado, la corriente J^μ corres-ponde solo a las llamadas corrientes libres, y no así a la corriente ligada, producida en los componentes de medio por su interacción con el campo electromagnético.

Las ecuaciones de campo son

más la identidad de Bianchi (3) por la forma de la definición de F. Por ejemplo, en el caso de cuatro dimensiones, en el sistema de referencia co-móvil al medio (i.e. en reposo respecto del mismo) la ecuación (24) se reduce a

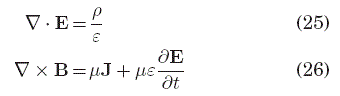
mientras que las leyes de Àmpere y Gauss del campo magnético, que provienen de la identidad de Bianchi (3), tienen la misma forma que en el caso de la ausencia de un medio,

3.1  Medio simple en un campo gravitacional y adición de un término de pseudo-Chern-Simons

La extensión de la acción (22) para la electrodinámica en un medio al caso de un espacio-tiempo curvo se logra aplicando nuevamente la pres-cripción de acoplamiento mínimo, sustituyendo la métrica de Minkowski por una métrica general . El resultado es

Esta prescripción transforma a la métrica óptica como sigue

donde supondremos que la dinámica del vector de velocidad u^μ está dada por y se supone que es tipo-tiempo , de modo que el medio puede interpretarse como una nube de polvo, o fluido incoherente. Para el caso de dimensión 2+1, añadamos el siguiente término a la acción

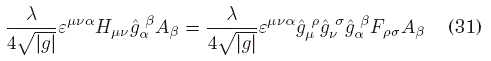
Aquí ε^μνα denota el símbolo de Levi-Civita. A pesar de la apariencia, este término ya no es un invariante topológico, debido a que el tensor necesita inevitablemente de la métrica para tener un índice arriba y el otro abajo, dado que u^μ se definió naturalmente como un vector, y no como una 1-forma. Desde el punto de vista de las derivadas funcionales, tenemos que

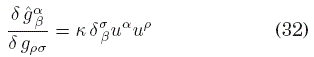
mientras que, si (31) fuese un auténtico término topológico, su derivada funcional respecto de la métrica debería ser nula, dado que tales términos no contribuyen al tensor energía-momento que eventualmente perturbaría al campo gravitacional. Sin embargo, es evidente que para κ = 0, se recupera la invariancia topológica, con lo que podemos decir que tal carácter es un límite de la teoría más general descrita por la acción

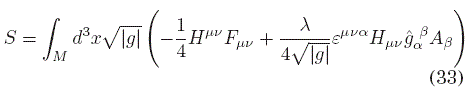
También, la invariancia de calibre del segundo término queda asegurada por la identidad de Bianchi y la antisimetría del tensor F.

Las ecuaciones de campo resultantes de la acción (33) son

A este nuevo término introducido en la acción, dado en (31), le llamamos de pseudo-Chern-Simons, o pseudo-topológico, ya que tiene al término ori-ginal de Chern-Simons como un límite, siendo κ una suerte de parámetro de control, y su introducción se ve motivada en el hecho de que es uno de los posibles acoplamientos no-triviales de un término auténticamente topológico a la métrica, valiéndonos de un vector característico del sistema, que es la 3-velocidad del medio óptico; además de los propios resultados que se mostrarán en lo que sigue, tocante a los efectos que este término tiene sobre la excitaciones masivas del campo electromagnético. Fenomenológicamente, como se señaló anteriormente, la conexión entre las teorías vectoriales de calibre en 2+1 dimensiones con límites de altas temperaturas en modelos en 3+1 dimensiones son una motivación para considerar esta modificación de la electrodinámica.

Otra vez, vale la identidad de Bianchi (3). Note que se ha supuesto implícitamente que el medio ocupa una región muy grande del espacio, de modo que los términos de frontera de las integraciones por partes pueden despreciarse. Para obtener una nueva generalización de la ecuación de Klein-Gordon, procedemos de manera análoga a la mostrada en la anterior sección. Tomamos la identidad de Bianchi y esta vez aplicamos el operador diferencial

de modo que tenemos

Pero ahora los conmutadores se escriben

Por otro lado, el tensor inverso de la métrica óptica puede hallarse fácilmente, y el resultado es

que llamaremos óptica métrica inversa. Entonces . Al contraer (34) con la métrica óptica inversa, obtenemos,

Ahora, definiendo otro dual , nuevamente de (34), puede probarse en forma simi-lar a (12), que

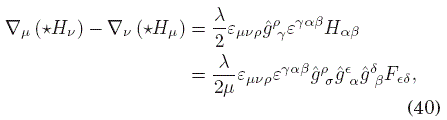
y puede probarse que el lado derecho es igual a

con

donde la última igualdad puede obtenerse usando el sistema de coordenadas co-móvil al medio, donde u^μ=(1,0,0). De modo que (40) se escribe

Luego, al sustituir las derivadas cruzadas de (36) usando el conmutador (37), sustituyendo los términos que tengan divergencias del tensor F con la ecuación (39), usando nuevamente la definición del dual y sustituyendo el resultado de (43), el resultado final para la generalización de la ecuación de Klein-Gordon en un espacio-tiempo arbitrario en presencia de un medio óptico es

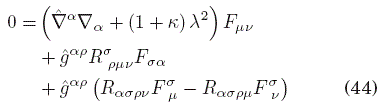
A continuación exploraremos las consecuencias de la ecuación (44) en los casos de espacio-tiempos maximalmente simétricos.

3.1.1  Espacio-tiempo plano

Dado que en un espacio-tiempo plano la curvatura es nula, podemos escoger coordenadas cartesianas globales, de modo que (44) se escribe

Es sugerente la analogía con la ecuación (5). Una solución de (45) es

donde C_μν es un tensor constante y q_ρ es un 3-vector de onda a determinar. Introduciendo esta expresión en la ecuación (45), se obtiene la siguiente relación de dispersión

de donde podemos concluir que, como en el caso del trabajo de Deser et al. , [1982], las excitaciones del campo son masivas, pero ahora el valor de la masa del campo es directamente proporcional al valor de las constantes ópticas del medio a través de κ = με−1=n²−1 > −1, donde n es el índice de refracción en reposo del medio óptico. Por otro lado, en el caso en que λ = 0, se tiene que la propagación del campo, en lugar de ser a través de geodésicas nulas en el espacio-tiempo de fondo, tiene lugar en geodésicas nulas de una nueva geometría Rieman-niana efectiva descrita por , como afirman Novello y Bittencourt , [2012]. De donde, en este nuevo caso, la propagación es a través de geodésicas tipo tiempo, como se esperaría en el caso de partículas masivas, pero ahora en una nueva estructura causal determinada por la métrica óptica.

3.1.2  En un espacio-tiempo de la familia de de Sitter

Tomemos nuevamente el caso del espacio tiempo descrito por la curvatura escalar constante R=6Λ. Procediendo de manera similar como en la sección 2.1, se tiene que

Ahora, invocando el resultado de la ecuación (42), y definiendo el campo magnético asociado al tensor de campo F_μν

y también el campo eléctrico,

se tiene de (48) que

y

Si llamamos al término masivo para el campo eléctrico, y al del campo magnético, las ecuaciones (51) y (52) se escriben

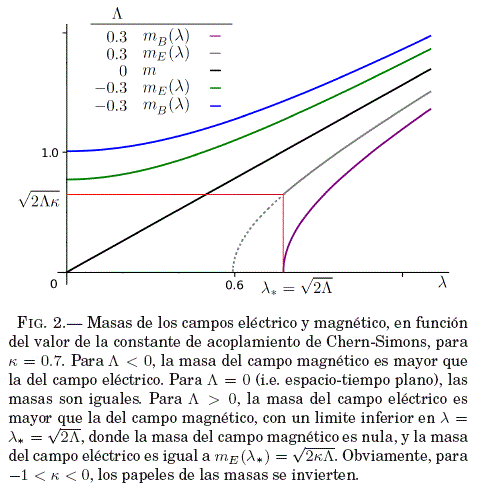
Es claro que existe una asimetría en el valor de las masas. Evidentemente, para un valor negativo de la constante cosmológica y para k > 0, la masa del campo magnético es mayor que la masa del campo eléctrico, y en este regimen, todos los valores de la constante de acoplamiento λ de Chern-Simons están permitidos; mientras que, para un valor positivo de la constante cosmológica, la constante de acoplamiento se restringe a λ² ≥ 2Λ, y aquí tendremos que la masa del campo eléctrico será mayor que la del campo magnético (ver Figura 2). Esos resultados sugieren una asimetría fundamental entre las partes eléctrica y magnética del tensor de campo, la cual se manifiesta no solo en el carácter tensorial de ambas partes en dimensiones diferentes a 3+1 (en 2+1, que es nuestro caso, el campo eléctrico es un 3-vector, mientras que el campo magnético es un campo escalar), sino que sus características inerciales son diferentes también, cuando interactúan con un medio óptico simple no-dispersivo, habiéndose considerado previamente la corrección de pseudo-Chern-Simons. Tal vez podría esperarse que para λ = 0 y constante cosmológica negativa, se recupere la simetría de masas; sin embargo, eso no sucede: aún si despreciamos la contribución pseudo-topológica (i.e., estudiamos la teoría de Maxwell solamente), encontraremos una asimetría en las masas de las partes eléctrica y magnética, como puede verse en las ordenadas en el origen de las curvas correspondientes a constante cosmológica positiva en la figura 2. A medida que el valor de κ se reduce acercándose a cero, la diferencia de masas se reduce, y cuando κ = 0, se recuperan los resultados de, por ejemplo, la figura 1, o también, la ecuación (48) se reduce a la ecuación (18). Los valores de las masas en este escenario son y . De la figura 2, más bien notamos que la presencia del término pseudo-topológico atenúa esta diferencia de masas a medida que crece el valor de la constante de acoplamiento λ.

Un límite interesante es aquel en que m_B=0, el cual se consigue haciendo λ²= λ_*² = 2Λ para Λ > 0. En tal caso, la masa del campo eléctrico es . En este límite, el campo magnético se propaga a través del medio a la velocidad a la que se propagaría un campo electromagnético de Maxwell, mientras que la parte eléctrica sufrirá un retraso debido a su carácter masivo. Ambas partes deben tener perfiles iniciales tales que las ecuaciones no-dinámicas de (34) se satisfacen (i.e.: las que no contienen derivadas temportales de los campos), más la identidad de Bianchi con índices espaciales (otra vez, una ecuación no dinámica).

 

4 Conclusiones

Escribimos una acción para la electrodinámica de Maxwell-Chern-Simons en 2+1 dimensiones, y obtuvimos una primera generalización de la ecuación de Klein-Gordon para el campo electromagnético (ecuación (13)). Al analizar el límite de un espacio maximalmente simétrico de la familia de de Sitter, se obtuvo una ecuación de onda masiva (ecuación (19)), cuya masa no solo depende de la constante de acoplamiento de Chern-Simons, como en el caso de un espacio-tiempo plano, sino que el valor de masa se ve afectado por la constante cosmológica. Aquí se pudo relacionar a la constante de acoplamiento con la constante cosmológica para obtener un límite no masivo, en el que el campo electromagnético se propaga a la velocidad de la luz, con perfiles iniciales restringidos por las ecuaciones de campo (20) más la parte no dinámica de la identidad de Bianchi.

Luego, se introdujo la presencia de un medio simple, haciendo uso de la métrica óptica de Gordon. Se escribió la acción de esta electrodinámica en un medio simple, introduciendo un término al cual llamamos de pseudo-Chern-Simons, debido a que su carácter de invariante topológico solo se conserva en el límite de vacío; obtuvimos las ecuaciones de campo, y una nueva generalización de la ecuación de Klein-Gordon para el campo electromagnético, con un acople no solo con el tensor de Riemann y contracciones, sino también con la métrica óptica. Aquí exploramos el caso de un espacio tiempo plano, y obtuvimos que los fotones masivos de la teoría se mueven a través de geodésicas tipo tiempo, pero en la geometría riemanniana efectiva de la métrica óptica. Luego exploramos un espacio-tiempo maximalmente simétrico con curvatura escalar diferente de cero, donde obtuvimos que, al separar al tensor de campo en sus compontentes eléctrica y magnética, éstas tienen masas diferentes, las cuales dependen de las constantes ópticas del medio, de la constante de acoplamiento de Chern-Simons, y de la constante cosmológica (ecuaciones (51) y (52)). Sin embargo, notamos que la diferencia de masas no se debe a la presencia del término pseudo-topológico, sino más bien a la presencia del medio óptico en el espacio-tiempo curvo considerado, ya que, como se ve en la figura 2, al hacer nula la constante de acoplamiento para constante cosmológica negativa, aún se tiene tal diferencia de masas, y más bien, al aumentar el valor de la constante de acoplamiento, esta dife-rencia se atenúa. Luego, sería un error atribuir esta diferencia al término pseudo-topológico. En lugar de eso, la introducción de este término proporciona un mecanismo teórico de atenuación de la diferencia de masas. Luego, la diferencia de masas (o también, la asimetría en las propiedades de propagación) se da en el escenario de un medio óptico teniendo un espacio-tiempo curvo de fondo. Note que son necesarias ambas cosas, ya que, como se vio, en un espacio tiempo plano pero con un medio óptico, no hay tal asimetría de masas, y en un espacio-tiempo curvo maximalmente simétrico pero sin el medio, tampoco existe esta asimetría.

Se señaló también la particular relevancia del límite en el que el campo magnético se propaga sin masa, mientras que el campo eléctrico tiene una masa proporcional al valor de las constantes ópticas del medio y al valor de la constante cosmológica, en el caso en el que esta última tiene un valor positivo.

Como perspectiva, queda el construir el forma-lismo hamiltoniano de esta teoría, lo cual no solo permitiría analizar la dinámica y los grados de libertad de calibre, sino que a partir de ahí se podría cuantizar la teoría, obteniéndose una teoría cuántica de campos en un espacio tiempo curvo. También, resta el analizar la estructura causal que surge de la métrica óptica y de la diferencia de masas de las componentes del tensor de campo electromagnético. Una perspectiva adicional es la de construir una teoría análoga con campos de calibre no abelianos.

 

Agradecimientos

Se agradece a Zui Oporto, Ph.D., por sus invalua-bles consejos para el desarrollo de este trabajo, y a Valeria Burgoa, por su ayuda con la elaboración de las figuras.

 

Conflicto de intereses

El autor declara que no hay conflicto de intereses con respecto a la publicación de éste documento.

 

References

[Deser et al. 1982]

Deser, S., Jackiw, R., & Templeton, S. (1982), Annals of Physics 140, 148.         [ Links ]

[Gordon 1923]

Gordon, W., (1923) Annals of Physics 22, 421        [ Links ]

[Jackson 1998]

Jackson, J. D. (1998). Classical Electrodynamics Third Edition (3rd ed.         [ Links ]).

[Landau y Lifshitz 1980]

Landau, L. D., & Lifshitz, E. M. (1980). The Classical Theory of Fields: Volume 2 (Course of Theoretical Physics Series) (4th ed.). Butterworth-Heinemann.         [ Links ]

[Misner et al 2017]

Misner, C. W., Thorne, K. S., Wheeler, J. A., & Kaiser, D., I. (2017). Gravitation. Princeton University Press.         [ Links ]

[Novello y Bittencourt 2012]

Novello, M., & Bittencourt, E. (2012) Phys. Rev. D 86, 124024        [ Links ]

[Thompson 2018]

Thompson, T. (2018) Phys. Rev. D 97, 065001        [ Links ]

[Weinberg 1978]

Weinberg, S. in Understanding the Fundamental Interactions, edited by A. Zichichi (Plenum, New York, 1978)        [ Links ]