A. ARTÍCULOS

 

Estudio teórico-experimental de la riqueza
dinámica del circuito de Hartley

 

Theoretical-experimental study of the
dynamic richness of the Hartley circuit

 

 

Abdias Sergio Callejas-Icuña^†, Aurelio Alejandro Suxo-Coro^‡, Gonzalo Marcelo Ramírez-Ávila^*
† Email: acallejasi@fcpn.edu.bo
^‡ Email: asuxoc@fcpn.edu.bo
^* Email: mravila@fiumsa.edu.bo
Recibido 2 de septiembre de 2021     Aceptado 5 de noviembre de 2021

 

 

---

Resumen

Estudiamos el comportamiento dinámico de una de las variantes del circuito de Hartley tanto desde el punto de vista numérico como experimental. Primero, observamos la transición delcomportamiento regular al caótico considerando como parámetros de control ya sea a los valores de una de las resistencias o uno de los inductores. Se obtuvieron experimentalmente los espacios de fase de los circuitos para diferentes valores de los parámetros de control. Utilizando software especializado para circuitos electrónicos, se corroboraron los resultados experimentales. Finalmente, caracterizamos el comportamiento dinámico del circuito asociándolo a un sistema dinámico. Integrando las ecuaciones del sistema dinámico, se obtuvieron los espacios de fase, diagramas de bifurcación y exponentes de Lyapunov. Los espacios de fase nos permitieron tener una visión cualitativa del comportamiento dinámico (regular o caótico) al observar la forma de los atractores obtenidos; en tanto que mediante los diagramas de bifurcación se visualizó la evolución en la transición de comportamiento regular a caótico o viceversa; además, de poderse observar también la ruta al caos a través de una cascada de desdoblamientos de período. Finalmente, el máximo exponente de Lyapunov nos permitió determinar cuantitativamente el comportamiento caótico o regular del sistema. Se encontró nuevamente una buena concordancia con nuestros resultados experimentales.

Descriptores: Simulaciones numéricas de sistemas caóticos - Dinámica no lineal y caos - Circuitos electrónicos.

---

Código(s) PACS: 05.45.Pq - 05.45.-a - 84.30.-r

---

Abstract

We study the dynamic behavior of a variant of Hartley's circuit from numerical and experimental viewpoints. First, we observed the transition from regular to chaotic behavior considering as parameter controls either the values of resistors or inductors. We experimentally obtained the phase space of the circuits for different values of the parameter control and using specialized software for electronic circuits, we corroborated the experimental results. Finally, we characterized the circuit's dynamical behavior with a related dynamical system determining phase spaces, bifurcation diagrams, and Lyapunov exponents. The phase spaces enabled us to have a qualitative insight into the dynamical behavior (regular or chaotic) when observing the shape of the related attractors. The bifurcation diagrams indicated how the dynamics evolve from regular to chaotic behavior or vice versa. Moreover, we observed the bifurcation cascade of doubling periods in the route to chaos. The largest Lyapunov exponent permitted us to eventually determine the chaotic or regular behavior of the system quantitatively, once more finding a good agreement with our experimental results.

Subject headings: Numerical simulations of chaotic systems - Nonlinear dynamics and chaos - Electronic circuits.

---

 

 

1  Introducción

Existe una variedad de circuitos electrónicos especializados para el estudio y comprensión de diferentes comportamientos dinámicos como ser el circuito de Chua o el circuito adaptado para el modelo de Rössler. Se han obtenido numerosos resultados teóricos y experimentales del comportamiento caótico con base en transistores como los estudiados por [ 2020 Semenov et.al.] y [2021 Behzad & Hamdipour ].

El circuito de Hartley fue ideado y descrito en 1915 y en su diseño original utilizaba un tubo al vacío; actualmente, se utilizan transistores. Hartley fue reconocido con la medalla de honor del Instituto de Ingenieros de Radio por este trabajo y su aporte a la teoría de la información. Los osciladores de Colpitts y de Hartley son circuitos muy conocidos y tienen un uso práctico en sistemas de telecomunicaciones; ambos circuitos presentan evidencia de comportamiento caótico como lo describen [ 2002 Kvarda] para el oscilador de Hartley y [ 1994 Kennedy] para el oscilador de Colpitts. Lo anterior significa que no solamente circuitos electrónicos diseñados específicamente pueden ser generadores de caos, sino también otros circuitos sin ese diseño específico.

Existen varias versiones del circuito de Hartley, pero teniendo todas ellas en común que están constituidas por dos partes: la primera jugando un rol amplificador que puede estar conformada por un transistor bipolar, un transistor de efecto de campo (FET) o un amplificador operacional; en tanto que la segunda, asociada a la resonancia por medio de un circuito tanque LC como lo señalan [ 2007 Malvino & Bates]. Estos circuitos también conocidos como osciladores de "tres puntos", tienen esta denominación debido a su configuración; ya que se forman a partir de conectar las tres terminales del bucle LC a los tres electrodos del transistor como se ve en la Fig. 1. Siendo X₁, X₂ y X₃ los elementos reactivos que pueden ser capacitores o inductores. Los circuitos de Colpitts y de Hartley son muy similares, siendo la diferencia más importante que el primero es un oscilador capacitivo de tres puntos con la configuración X₁, X₂ capacitores y X₃ inductor; en tanto el de Hartley es un oscilador inductivo con X₁, X₂ inductores y X₃ capacitor.

Para el estudio del caos se requiere de al menos dos ecuaciones no autónomas o tres ecuaciones diferenciales autónomas de primer orden. Para el primer caso el circuito debe contar con dos elementos reactivos y una fuente dependiente del tiempo; mientras que para el segundo se deben tener tres elementos reactivos que es el caso del circuito de Hartley, como lo indica [ 1987 Hasler].

Este trabajo se divide en tres partes; en la primera se muestra las ecuaciones que modelan el comportamiento del circuito de Hartley, en la segunda se realiza un estudio del comportamiento dinámico haciendo uso de las herramientas de la dinámica no lineal; específicamente, diagramas de bifurcación y exponentes de Lyapunov. La tercera describe los resultados experimentales obtenidos. Finalmente, se dan las conclusiones y perspectivas de este trabajo.

 

2 Circuito de Hartley

En este trabajo se estudia la versión del circuito de Hartley dada por [ 2002 Kvarda]; la cual consiste en un transistor bipolar Q₁, dos inductores L₁ y L₂ cada uno en serie con una resistencia R _L1 y R_L2 respectivamente, un resistor lineal R_L y un capacitor lineal en paralelo con una resistencia R_C, como se muestra en la Fig. 2. Las ecuaciones que gobiernan el sistema se muestran a continuación:

Las Ecs. (1) y (2) son obtenidas aplicando las leyes de Kirchhoff, en tanto las Ecs. (3) y (4) son las que modelan el comportamiento del transistor PNP 2N3906; donde I_B es la corriente de base, V_EC es el voltaje del emisor-colector, V_TH es el voltaje umbral del transistor, V_EB es el voltaje entre el emisor y la base, V_EC0 es el voltaje restante en el transistor abierto y k es la pendiente de conmutación que se define como una relación entre |ΔV_EC| y |ΔV_EB|. Los parámetros del circuito donde se evidenció comportamiento caótico son: V₁ = 3.75 V, R_L1=1.5 Ω, R_L2 = 1.5 Ω, L₁ = 100 μH, L₂ = 100 μH, C₁ = 22 nF, R_C = 95.5 Ω, R_L = 76 Ω, B_F = 180, k = 900, V_TH = 0.75 V, V_EC0 = 0.2 V y R_0N = 100 Ω.

 

3 Modelo

Las variables de estado (magnitudes dinámicas) son: el voltaje del capacitor V_C, las corrientes del circuito I₁ e I₂; estas se pueden normalizar respecto a V_TH, I₀ y τ₀, donde de esta forma introducimos las variables de estado adimensionales: x₁, x₂ y x₃ tal que V_C = V_TH • x₁, I₁ = I₀ • x₂, I₂ = I₀ • x₃ y t = τ₀• τ así la Ec. (1) queda como:

Se resuelven las Ecs. (2)-(4) para que V_EC e I_B estén en función de las variables adimensionales. Por tanto quedarían respectivamente de la siguiente forma:

Los diagramas de bifurcación son una herramienta fundamental para el estudio de comportamientos dinámicos; estos se obtienen a partir de la resolución numérica del sistema de ecuaciones. Estos diagramas muestran el comportamiento global del sistema cuando se varía uno de los parámetros, lo que modifica las variables de estado. El tiempo de integración debe ser lo suficientemente largo para garantizar que se ha superado el transitorio. Los exponentes de Lyapunov que se utilizan para cuantificar la tasa de divergencia o convergencia de dos soluciones que difieren en sus condiciones iniciales por una perturbación infinitesimal, constituyen también otra herramienta de análisis. El espectro de Lyapunov contiene un número de exponentes de Lyapunov igual a la dimensión del espacio de fases. El máximo exponente de Lyapunov (MEL) determina el comportamiento del sistema dinámico. Si el MEL es positivo, el comportamiento es caótico, en tanto que si es negativo, el compartimento es regular. En flujos, el máximo exponente de Lyapunov (MEL) se define excluyendo el exponente de Lyapunov correspondiente a la dirección de la trayectoria. En esta dirección el exponente siempre es nulo, lo que impide que el MEL tome valores negativos. Para el cálculo del MEL se utiliza la matriz jacobiana.

donde F′₁(x₃) y F′₂(x₃) son las derivadas de las funciones por partes:

4 Resultados

4.1 Integración Numérica

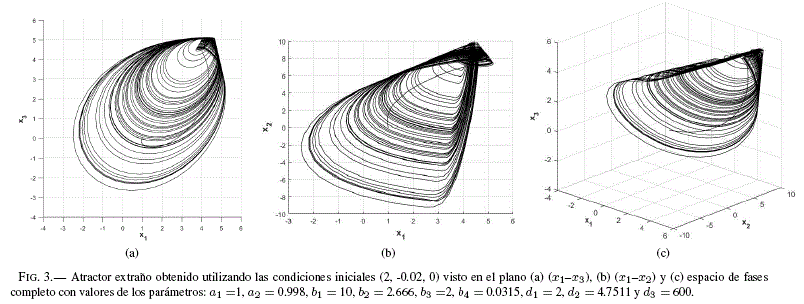
Con las Ecs.  (5)-(7) se pudo verificar el comportamiento caótico reportado por [ 2002 Kvarda]. El atractor extraño fue encontrado a partir de la integración numérica utilizando el método de Runge-Kutta 4 y 5, con condiciones iniciales (2, -0.02, 0). El atractor obtenido se muestra en la Fig. 3. Igualmente, integrando el sistema descrito por las Ecs. (5) se obtuvieron los diagramas de bifurcación mostrando la dinámica de la variable x₁ cuando los parámetros de control son R_L en el rango [0, 300] Ω (Fig. 4(a)) y L₁ en el intervalo [55, 120] μH (Fig. 5(a)). También se obtuvieron los MELs en el mismos rangos, como se muestran en las Figs. 4(b) y 5(b). Para la obtención de los diagramas de bifurcación, el tiempo de integración numérica fue de 7000, con un transitorio de 6950, un paso de 0.01 y 15000 valores del parámetro de control, haciendo un total de 1.05×10 ¹⁰ cálculos para la Fig. 4(a); en tanto que para la Fig. 5(a) el paso fue de 0.05 y el número de valores para el parámetro de control de 1625 dando un total de 2.275×10 ⁸ cálculos. Lo anterior muestra que se requiere una capacidad computacional elevada.

Para encontrar el MEL en ambos casos el tiempo de integración numérica fue de 2500 para cada valor del exponente de Lyapunov, con un paso de 0.01. Para la construcción de cada diagrama solo se almacena el ultimo valor. Es importante recalcar que a pesar de tener los tiempos de integración mencionados, estos resultan ser cortos para tener una buena resolución de los diagramas de bifurcación y de los MELs.

En el diagrama de bifurcación de la Fig. 4(a) se observa que a medida que aumentamos el parámetro de control R_L surgen nuevas ramas de comportamiento estable; así, a partir de la región (A) se observa desdoblamiento de periodo hasta entrar en una región caótica definida por la región oscura en (B) ya que se tiene una cascada infinita de duplicaciones de período. En la región (C) podemos observar tres ramas estables que indican ciclo de periodo 3 (salida de la ventana caótica). La región (D) muestra otra vez un comportamiento caótico, mientras que en (E) se tiene periodo dos; finalmente, un comportamiento regular en (F).

La constatación del comportamiento dinámico del sistema se verificó con el cálculo de los MELs. En la Fig. 4(b) las flechas indican las mismas regiones del diagrama de bifurcación, el comportamiento regular y caótico se puede evidenciar ya que el MEL es positivo en regiones caóticas como (B) y (D), negativo en regiones regulares como (A), (C), (E) y (F). La región indicada por (B1) tiene valores negativos del MEL y por lo tanto un comportamiento regular, este caso no es posible distinguirlo en el diagrama de bifurcación, pero si se pudo observar en el experimento.

En el diagrama de bifurcación correspondiente al parámetro de control L₁ (ver Fig. 5(a)) se observa comportamiento regular en la región (A), desdoblamiento de periodo en (B), un desdoblamiento de periodo 4 en (C), una región caótica en (D) manteniendo fija la resistencia R_L en 76 Ω. En el diagrama del MEL mostrado en la Fig. 5(b) las flechas indican las mismas regiones que en el diagrama de bifurcación, donde se pueden distinguir regiones con exponente es negativo como en (A), (B) y (C); ademas de una región (D) con MEL es positivo.

 

 

 

4.2 Implementación experimental

Se armó el circuito de Hartley en un protoboard según el esquema de la Fig. 2 con valores de los componentes dados en la Tabla 1, los cuales fueron obtenidos utilizando un multímetro digital LCR-T4 y un LC-Meter de [ 2020 Rice], que se construyó para medir la inductancia y capacitancia con precisión elevada. Por otra parte se utilizó un osciloscopio Unit UTD2072CEXII de dos canales con ancho de banda de 70 Mhz y 1 GS/s de muestreo, ademas de una fuente varia-ble de [1.5, 7.5] V construida a partir de el circuito integrado LM317.

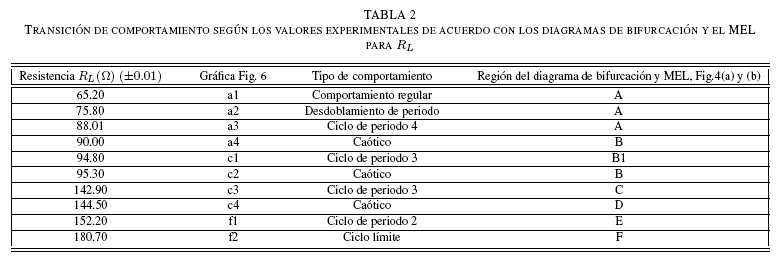
En la Fig. 6, se visualizan los resultados experimentales y de simulaciones en LTspice. Se realizó la variación del parámetro R_L, para lo que se utilizó una resistencia variable de 500 Ω. Por otra parte los canales 1 y 2 del osciloscopio se conectaron a los nodos N1 y N2 respectivamente, como se mostró en la Fig.2; esto para tener lecturas del voltaje en el capacitor V_C y en la resistencia V_RL. Se obtuvieron diferentes tipos de comportamiento basados en las regiones del diagrama de bifurcación de la Fig.4(a), lo que se describe en la Tabla 2. Cabe señalar que debido a la incertidumbre de los valores utilizados, no se encontró el comportamiento en los valores precisos que se indican en el diagrama de bifurcación; sin embargo, se observó el comportamiento cualitativo del mismo. En las simulaciones se utilizaron los mismos valores que reportó [ 2002 Kvarda]. El tiempo de simulación fue de 2.0 ms y solo se almacenaron datos desde 1.8 ms para todas las gráficas mostradas; esto para salir del régimen transitorio.

La región B1 mostrada en el diagrama de exponentes de Lyapunov Fig.4(b), es verificada experimentalmente en la Fig.6(c1), teniendo un ciclo de periodo 3.

Se realizó la variación del parámetro L₁ (ver Fig.7), para lo que se construyeron inductores con valores aproximados de 50 μH, 80 μH y 100 μH con resistencia interna de 0.2 Ω. Sin embargo para un mejor estudio en la transición de estados, se construyó un inductor variable que tiene un rango de [50, 100] μH con resistencia interna de 1.7 Ω. Se observó que con estos valores de resistencia interna el funcionamiento del circuito no se ve afectado. La verificación del comportamiento dinámico respecto al inductor L₁ es descrito en la Tabla 3. La resistencia R_L se fija en 162.4 Ω, ya que con este valor se pudieron observar cambios en el comportamiento al variar el valor de la inductancia; esta falta de precisión puede ser debida a la resistencia interna del inductor variable, a la resistencia interna de la fuente de voltaje o a la incertidumbre de los componentes utilizados. Lo anterior puede afectar también a la precisión cuando se verifican los diferentes diagramas; ya que en el análisis numérico y las simulaciones en LTspice, los factores como las resistencias internas así como también su capacitancia parásita no está considerada. En la Fig. 8 se muestra el atractor extraño obtenido con los valores indicados en la Tabla 1.

 

5 Conclusiones y Perspectivas

Se trabajó con las ecuaciones normalizadas y se realizó el estudio y clasificación del comportamiento dinámico del circuito de Hartley variando los parámetros R_L y L₁. Se observó la ruta al caos a través del desdoblamiento de periodos tanto en simulaciones como experimentalmente; encontrándose una buena correspondencia cualitativa con los diferentes diagramas de bifurcación. Se pudo constatar que los MELs constituyen una herramienta muy útil que puede respaldar lo que se observa en los diagramas de bifurcación. Los diagramas de bifurcación muestran el comportamiento del circuito cuando se varia un parámetro de control. Una mejor resolución está ligada al aumento del tiempo de integración. La potencia computacional exigida para esto es grande por lo que se suele paralelizar los procesos y utilizar clusters. La resistencia interna de los diferentes componentes es también un aspecto importante a la hora de realizar el experimento. El uso de simuladores de circuitos tales como LTspice es muy práctico para el estudio de comportamientos dinámicos en un circuito. Se entiende que muchos circuitos comunes pueden ser generadores de caos y estos comportamientos se pueden determinar realizando este tipo de estudios. El éxito de este trabajo en la determinación de los comportamientos dinámicos en el circuito de Hartley fue fruto del exhaustivo trabajo experimental. Lo anterior abre la posibilidad de continuar con la investigación del circuito de Hartley de dos componentes como el expuesto por [ 2012 Tchitnga et.al.], además del desafío en la descripción experimental de la aniquilación de las estructuras denominadas "camarones" que fue obtenida numéricamente por [ 2021 Ramírez-Ávila, Kurths & Gallas]. Finalmente se pretende profundizar en el análisis numérico de este sistema.

 

Agradecimientos

A.S.C.I. agradece al Dr. Hugo Rivera como también al Dr. Wilfredo Tavera por sus críticas y observaciones en el desarrollo del trabajo. Así mismo los autores agradecen a los árbitros por sus comentarios los mismos que coadyuvaron a su mejora.

 

Conflicto de intereses

Los autores declaran que no hay conflicto de intereses con respecto a la publicación de éste documento.

 

References

[2002 Kvarda]

kvarda Kvarda, P. 2002, International Journal of Bifurcation and Chaos, 12, 2229.         [ Links ]

[ 2020 Semenov et.al.]

Semenov, A., Havrilov, D., Volovik, A., Baraban, S., Savytskyi, A. & Zviahin, O. 2020, IEEE 15th International Conference on Advanced Trends in Radioelectronics, Telecommunications and Computer Engineering, 25.         [ Links ]

[ 2021 Behzad & Hamdipour ]

Behzad, F. & Hamdipour, M. 2021, Pramana - Journal of Physics, 95, 2.         [ Links ]

[ 1994 Kennedy]

Kennedy, M.P. 1994, IEEE Transactions on Circuits and Systems I, 41, 11.         [ Links ]

[ 2007 Malvino & Bates]

Malvino, A. & Bates, D. 2007, Principios de electrónica, (Madrid: McGraw-Hill/Interamericana de España).         [ Links ]

[ 1987 Hasler]

Hasler, M.J. 1987, Proceedings of the IEEE, 75, 1009.         [ Links ]

[ 1984 Matsumoto]

Matsumoto, T. 1984, IEEE Transactions on Circuits System, 31, 1055.         [ Links ]

[ 2004 Govorukhin & Gallas]

Govorukhin, V., 2004, "Calculation Lyapunov Exponents for ODE", Website: https://www.mathworks.com/matlabcentral/fileexchange/4628-calculation-lyapunov-exponents-for-ode. Acceso: 5.5.2022.         [ Links ]

[ 1985 Wolf & Swift]

Wolf, A., Swift, J. B., Swinney, H. L. & Vastano, J. A. 1985, Physica D, 16, pp. 285-317.

[ 2020 Rice]

Rice, P. 2020, Phil Rice's Homepage, "LC-Meter", Website: https://sites.google.com/site/vk3bhr/home?authuser=0. Acceso: 6.12.2021.         [ Links ]

[ 2009 Fortuna, Frasca & Xibilia]

Fortuna, L., Frasca, M. & Xibilia, M. G. 2009, Chua's circuit implementations: yesterday, today and tomorrow (Singapore: World Scientific Publishing).         [ Links ]

[ 2014 Freire & Gallas]

Freire, J.G. & Gallas, J.A.C. 2014, Chaos, Solitons & Fractals, 59, 129.         [ Links ]

[ 2012 Tchitnga et.al.]

Tchitnga, R., Bertrand F. H., Nana B., Louodop Fotso, P. H. & Woafo, P. 2012, Chaos, Solitons & Fractals, 45, 306.         [ Links ]

[ 2021 Ramírez-Ávila, Kurths & Gallas]

Ramírez-Ávila, G.M., Kurths, J. & Gallas, J.A.C. 2021, Chaos, 31, 101102        [ Links ]