B. CONTRIBUCIONES Y REVISIONES

 

Análisis de un modelo matemático simple para la descripción de propagación de COVID-19

 

Analysis of a simple mathematical model for describing the COVID-19 spreading

 

 

Juan Dennis Tejeira-Huacani^†
†jtejeirah@fcpn.edu.bo
Carrera de Física, Universidad Mayor de San Andrés
Campus Universitario, c. 27 Cota-Cota, Casilla de Correos 8635
La Paz - Bolivia

 

 

---

Resumen

Se realizó el análisis de la propagación epidémica usando una modificación del modelo SIR para el COVID-19. Mediante un análisis de estabilidad lineal se muestra que los estados asociados a los puntos fijos llegan a ser inestables. Además se hace un análisis de la dinámica del sistema considerando medidas de contención, y se concluye que estas son útiles para disminuir el número de personas infectadas.

Descriptores: Enfermedades - educación - dinámica no lineal.

Código(s) PACS: 87.19.xd, 01.40.-d, 05.45.-a

---

Abstract

The analysis of the epidemic spread was carried out using a modification of the SIR model for the COVID-19 virus. A linear stability analysis shows that the fixed states become unstable. In addition considering containment measures of the system it is concluded that these measures are useful to reduce the number of infected people.

Subject headings: Diseases - education - nonlinear dynamics.

---

 

1  Introducción

La humanidad ha estado en contacto con agentes patógenos desde mucho tiempo atrás. Patologías como la influenza o el SARS, vinculadas a virus causaron desastres a nivel económico-social en los últimos años; sin embargo, siempre fue posible encontrar soluciones gracias al trabajo de la comunidad científica.

Por un lado, los biólogos realizan estudios de los anticuerpos necesarios para combatir la enfermedad. Por otra parte, los químicos y bioquímicos se encargan de analizar las reacciones que suceden al operar con ciertos compuestos. Finalmente, los médicos son los que se ocupan de optimizar los tratamientos a través del suministro de medicamentos y vacunas cuando es posible.

Otros científicos de las denominadas ciencias duras también cumplen una función muy importante, que consiste en la formulación de modelos que puedan ayudar a tomar decisiones paliativas y de contingencia de la epidemia. Sin embargo, somos concientes que dadas las características del sistema a estudiar, estos modelos tienen un poder predictivo limitado en el tiempo como lo apunta Manrubia, [2020].

La herramienta matemática que nos permite realizar esto es el análisis de los sistemas de ecuaciones diferenciales no lineales compartimentales, que expresan el cambio de las variables dinámicas en un intervalo de tiempo, como es el caso de los modelos epidemiológicos. En particular, la epidemiología de las enfermedades virales es una disciplina que se encarga del estudio de factores determinantes, predicciones y control de los factores relacionados con las implicaciones correspondientes en lo que a la salud se refiere tal como Pliego Pliego, [2011] lo indica.

El centro de estudio de estos modelos epidemiológicos es la dinámica de la transmisión de una cierta enfermedad. Esto nos permite seleccionar un determinado modelo basado en dicha dinámica. En este artículo se realizará el estudio de la propagación de COVID-19.

El coronavirus tipo 2, responsable del sindrome respiratorio agudo grave (SARS-CoV-2) es el virus causante de la enfermedad del mismo nombre. Su expansión mundial ha generado una pandemia que causó diversas reacciones en cada país. La transmisión de este virus ocurre a través de la difusión de pequeñas gotas de saliva que se emiten al hablar, estornudar o respirar, que al ser expelidas por un portador (que posiblemente no presente ningún síntoma) pueden pasan directamente a otra persona mediante la inhalación.

Un hecho importante sobre la enfermedad es que un infectado no presenta síntomas de la enfermedad hasta una semana después en promedio. Esto causa un gran peligro, pues es difícil de identificar un foco de infección para iniciar un aislamiento del enfermo. Otro dato es que el período de recuperación en promedio es de 25 días con hospitalización como lo señala la Organización Mundial de la Salud, [2020].

El presente artículo inicia con la presentación a modelos epidemiológicos como el SIR y el SAIR. Posteriormente, haciendo uso del segundo modelo mencionado, se realiza el análisis de poblaciones observando los estados asociados a puntos fijos. Se escoge un conjunto de parámetros adecuados, obteniéndose la evolución del número de casos positivos (infectados) para el país, lo que se compara con los datos oficiales reportados por las autoridades de salud bolivianas. Finalmente, se dan las conclusiones y perspectivas del trabajo.

 

2  Modelos epidemiológicos

Existen muchos modelos epidemiológicos que son capaces de describir la propagación de epidemias. Aquí se tratarán el modelo SIR y una modificación del mismo denominada modelo SAIR.

2.1  Modelo SIR

El modelo epidemiológico SIR es un modelo que contempla a tres tipos de poblaciones de individuos: susceptibles S, infectados I y removidos R. Este modelo se describe porlas siguientes relaciones:

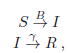
donde B y γ son las tasas de infección y recuperación respectivamente. Para el caso del coronavirus usamos γ = 1/25. Considerando que la tasa de infección incrementa si la cantidad de infectados es mayor, por lo que se puede considerar que B es:

Siendo β la cantidad de contagios por infectado y N es la población total. De esta manera, las ecuaciones diferenciales asociadas al sistema dinámico son:

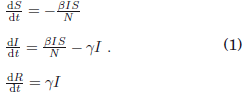
2.2  Modelo SAIR

Este modelo resulta de introducir un nuevo tipo de población en el modelo SIR, la cual corresponde a los individuos asintomáticos A. Por consiguiente, el modelo SIR se modifica de manera que las interacciones compartimentales quedan como lo señalan Gutiérrez & Varona, [2020]. De acuerdo con lo anterior, la introuducción de la población de un nuevo grupo, conduce a que las interacciones compartimentales tomen la forma:

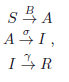
donde los coeficientes B y γ mantienen sus definiciones expuestas anteriormente, y σ es el intervalo de tiempo en el cual un individuo asintomático llega a presentar los síntomas respectivos de la enfermedad. En el caso del COVID-19, se considera σ = 1/7. De esta manera, las ecuaciones diferenciales de este sistema son:

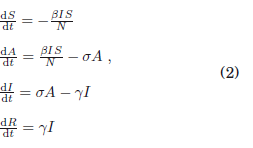
que es el modelo que se utiliza en el análisis.

 

3  Análisis del modelo SAIR

A partir de las Ecs. (2), se realiza un análisis de estabilidad lineal tal como lo explica Nicolis, [1995], encontrándose como punto fijo el mostrado en la Tabla 1:

Table 1: Punto fijo 1 del sistema.

También se encuentran los autovalores:

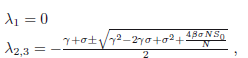
de donde se tiene que la estabilidad del sistema dependerá de los valores de los parámetros y la condición inicial para la población de individuos susceptibles. Se consideran los datos correspondientes a Bolivia. Se toma una población de N=10627269 habitantes. El modelo de predicción indica la evolución mostrada en la Fig. 1 donde se comparan la curva obtenida mediante el modelo con los datos oficiales dados por las autoridades de salud contenidos y reportados por Observatorio del Gobierno Autónomo Municipal de La Paz, [2020]

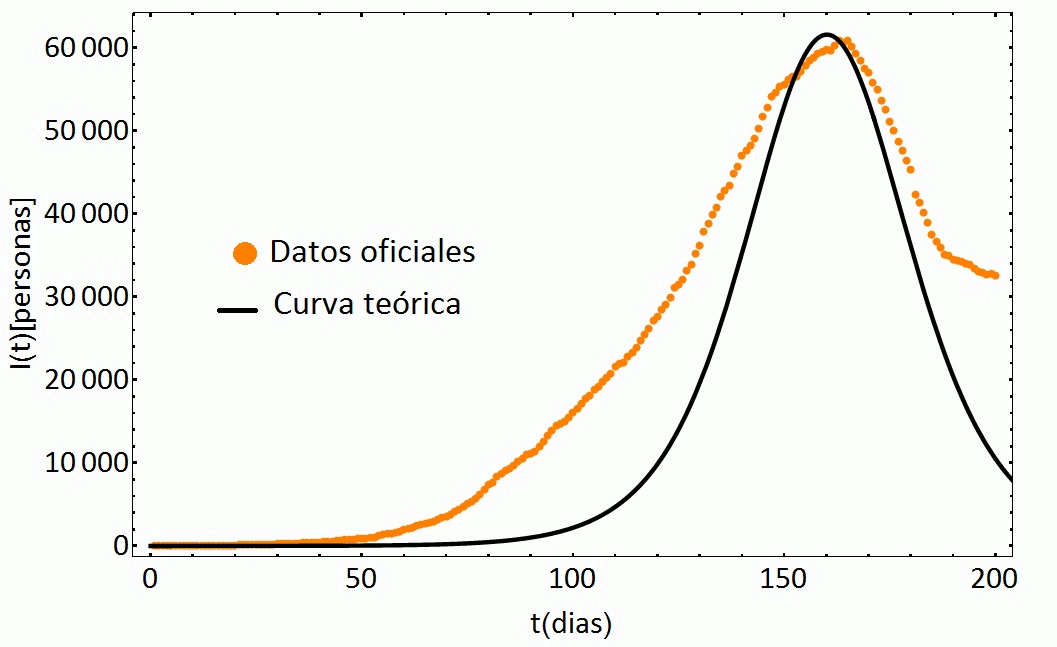
Figure 1: Curva de evolución de individuos infectados utilizando el modelo SAIR con condiciones iniciales S₀=10627267, A₀=2, I₀=0, R₀=0, con valores para los parámetros: N=10627269, β = 1.15, γ = 0.97, σ = 0.85; comparada con la evolución de infectados construída a partir de datos oficiales.

Como se puede notar, existe una relativa concordancia entre la curva obtenida mediante el modelo y los datos oficiales del número de individuos infectados Las discrepancias pueden deberse a múltiples aspectos, entre los que se pueden mencionar:

• La no consideración en el modelo de los individuos que fallecen

• El carácter global que se le da al modelo cuando pertienentemente se conoce que cada región tiene su propia dinámica

• Las incertidumbres que se pueden tener con los datos oficiales

• La difícil identificación de los individuos asintomáticos.

• El modelo no considera las medidas de contención adoptadas.

 

4  Conclusiones y Perspectivas

El modelo SIR modificado es una herramienta muy útil para reproducir de manera aproximada la evolución de cada población ya permite inferir los aspectos ligados a la estabilidad, pues ante una variación se pueden obtener resultados completamente diferentes. Aunque el modelo permite una descripción aproximada en lo que se refiere al máximo número de infectados de lo que se podría llamar una "primera ola", encontramos algunas deficiencias del modelo a nivel conceptual; por ejemplo, el considerar que la población total se mantiene constante, cuando pertinentemente se sabe que una parte de los infectados puede llegar a morir. Está claro que el modelo puede ser mejorado y refinado para obtener comportamientos más realistas y así poder tener la chance de darle un carácter predictivo como es deseable. Los aspectos ligados a los efectos de las medidas de contención podrían ser tenidos en cuenta mediante la introducción de incrementos dinámicos del parámetro β, el cual pasaría a ser función del tiempo Finalmente, aspectos tales como la existencia de vacunas podrían también ser incorporados en el sistema dinámico, constituyendo los individuos vacunados, un nuevo compartimiento poblacional.

Conflicto de intereses El autor declara que no hay conflicto de intereses con respecto a la publicación de éste documento.

 

References

[Gutiérrez & Varona 2020]

Gutiérrez J. M. & Varona J. L. 2020, "Análisis del COVID-19 por medio de un modelo SEIR". https://institucional.us.es/blogimus/2020/03/covid-19-analisis-por-medio-de-un-modelo-seir/         [ Links ]

[Manrubia 2020]

Manrubia, S. 2020, Physics, 13, 166         [ Links ]

[Nicolis 1995]

Nicolis, G 1995, Introduction to Nonlinear Science, (Cambridge: Cambridge University Press).         [ Links ]

[Observatorio del Gobierno Autónomo Municipal de La Paz 2020]

Observatorio del Gobierno Autónomo Municipal de La Paz Estadísticas de Casos Confirmados de Coronavirus en Bolivia. http://observatoriocovid19.lapaz.bo/observatorio/index.php.        [ Links ]

[Organización Mundial de la Salud 2020]

"Brote de Enfermedad por Coronavirus: Orientaciones" 2020. En el Sitio WEB de la Organización Mundial de la Salud. https://www.who.int/es

[Pliego Pliego 2011]

Pliego Pliego, E .C. 2011, "Modelos Epidemiológicos de Enfermedades Virales Infecciosas", en Tesis de Licenciatura en Matemáticas en la Benemérita Universidad Autónoma de Puebla.        [ Links ]