Número Efectivo de Reproducción del COVID-19 en Bolivia

Bellot, Daniel

Servicios Personalizados

Revista

Articulo

Indicadores

Citado por SciELO
Accesos

Links relacionados

Similares en SciELO

Otros
Otros

Permalink

Revista Boliviana de Física

versión On-line ISSN 1562-3823

Revista Boliviana de Física v.37 n.37 La Paz dic. 2020

A. ARTÍCULOS

Número Efectivo de Reproducción del COVID-19 en Bolivia

Effective reproduction number of covid-19 in Bolivia

Daniel Bellot
(Recibido 5 de diciembre de 2020; aceptado 29 de diciembre de 2020)

Resumen

El número básico de reproducción, R₀, es un parámetro ampliamente usado en modelos epidemiológicos. La naturaleza no lineal de la dispersión de un virus en una población humana limita el valor predictivo de R₀ a un periodo breve al inicio de una pandemia. Se presenta un método que actualiza el valor de R₀ a un valor efectivo (R_t) basado en la evolución del número de casos, lo cual hace posible conservar la vigencia de los modelos epidemiológicos más allá de la etapa inicial. El método se basa en el trabajo de Bettencourt y Ribeiro, que consiste en un esquema bayesiano que estima la distribución de probabilidad de R_t. Una implementación de este modelo en Python realizada por Kevin Systrom se ha adaptado para analizar los datos reportados en el sitio oficial del Gobierno de Bolivia sobre el COVID-19. Se ha obtenido una estimación de R_t y su evolución temporal para cada Departamento y para Bolivia en su conjunto. También se discuten las posibles aplicaciones de proyecciones basadas en este modelo.

Descriptores: Modelos matemáticos - número de reproducción - enfermedades.

Código(s) PACS: 87.10.+e, 87.17.Ee, 87.19.xd

Abstract

The basic reproduction number, R₀ is a widely used parameter in epidiemological models. The non-linear nature of the spread of a virus in a human community limits the predictive value of R₀ in the early stages of a pandemic. A method is presented which updates the R₀ value to an effective value (R_t) based on the evolution of the number of cases, which makes it possible to preserve the validity of the epidiemological models, beyond the early stages. This method is based on Bettercourt and Ribeiro's work, and it consists of a bayesian scheme which estimates the distribution of probability of R_t. An implementation of this model on Python undertaken by Kevin Sytrom has been adapted to anlayze the data reported on the official website of the Bolivia government about COVID-19. An estimation for R_t and its temporary evolution for every department in Bolivia and the country as a whole was obtained. Finally possible application of projections based on this model are discussed.

Subject headings: Mathematical models - diseases - reproduction number.

1 Introducción

El Número Básico de Reproducción R₀, es una métrica epidemiológica usada para describir la transmisibilidad de agentes infecciosos [[42019Delamater et al.]]. Se define como el número de nuevos casos que un caso genera en promedio en el transcurso de su periodo infeccioso[62009Fraser et al.]. El valor de R₀ depende de factores biológicos, sociales y ambientales que gobiernan la transmisión de patógenos [[42019Delamater et al.]]. Su importancia radica en que provee una estimación del potencial epidemológico de un virus en un modelo de sencilla interpretación.

El crecimiento inicial de una enfermedad infecciosa depende fuertemente del valor que adopte R₀ en una determinada población, si R₀ es mucho menor a 1 el número de casos decrecerá rápidamente, todo lo opuesto si R₀ es mucho mayor a 1. Cuando R₀ es igual a 1 el número de casos activos se mantendrá constante en el tiempo [[112020Systrom]]. R₀ es rara vez medido directamente, y los valores que adopta son dependientes de las suposiciones y estructura de los modelos [[42019Delamater et al.]]. [82020Liu et al.Liu, Gayle, Wilder-Smith, & Rocklöv] recopila los resultados de 12 estudios sobre el COVID19 que reportan valores entre 1.5 y 6.68, la Organización Mundial de la Salud inicialmente reportaba un valor de 2.7. Posteriores estudios reportan valores cercanos a 6.

Table 1:

Valores de R₀ para algunas enfermedades.

En la práctica, los datos epidemiológicos típicamente permiten solo una estimación del número efectivo de reproducción R_t [[32008Bettencourt & Ribeiro]], que puede diferir de R₀ debido a inmunidad adquirida y otros factores. Para una enfermedad infecciosa emergente, cuando la transmisión es incipiente y el patógeno esta en proceso de adaptarse a la población, se vuelve crucial el monitoreo cuantitativo de la variación temporal del número de reproducción efectiva. De esta manera, el seguimiento a una enfermedad emergente se puede formalizar en términos del monitoreo de R_t [[32008Bettencourt & Ribeiro]].

1.1 Relaciones con el modelo SIR y la Tasa de Duplicación

El modelo SIR (Suceptible-Infectado-Removido) es uno de los modelos matemáticos más fundamentales de la epidemiología [[71927Kermack & McKendrick]], su formulación consiste de un sistema de ecuaciones diferenciales ordinarias.

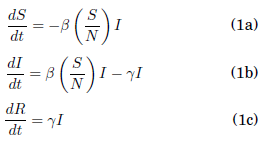
Donde N representa el número de habitantes de la población, S representa el número de individuos suceptibles a la enfermedad, I representa el número de infectados R representa el número de individuos inmunizados (removidos) a la enfermedad ya sea por recuperación o fallecimiento, β representa la tasa de transmisión de la enfermedad y γ representa la tasa de recuperación (siendo 1/γ el periodo medio de recuperación). En términos de los parámetros de este modelo el número efectivo de reproducción R_t esta definido por la siguiente ecuación:

La tasa de duplicación de casos esta íntimamente relacionada con el número de reproducción, ambos cuantifican la rapidez con la cual una enfermedad se propaga en una población. Formalmente es indistinto formular la variación del número de casos mediante el uno o la otra, la diferencia práctica es la facilidad interpretativa que brinda cada uno. En el contexto del modelado matemático resulta conveniente el uso de un parámetro adimensional como lo es R_t, en cambio, en un ámbito administrativo o médico puede ser más intuitivo referirirse a una tasa temporal. La relación matemática entre el número de reprodución R_t y la tasa de duplicación T_d es la siguiente:

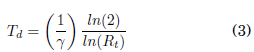
Un factor a favor de usar R_t en lugar de la tasa de duplicación es que el valor umbral entre una tendencia al crecimiento y una tendencia a decrecer es claramente el valor 1, el valor de este umbral no es evidente en el caso de tiempo de duplicación. El propósito final de este artículo es incentivar el uso del número R_t como medio de estimación del impacto local de las medidas sanitarias en el desarrollo una pandemia.

2 Modelo para estimar el valor actual R_t

El modelo que se detalla a continuación provee una estimación del valor de R_t basada en una serie temporal con los datos más recientes. Al existir un retraso entre el contagio y la detección de la enfermedad, esta estimación corresponde a cierto número de días en el pasado. Por sí solo, este modelo no realiza una predicción a futuro de R_t o del número de casos.

En una sección posterior se aplica un método diferente para realizar una proyección del número de casos basada en el valor de R_t obtenido de este modelo.

2.1 Fuentes de Datos

Entre Marzo 2020 y Julio 2020 se han reportado diariamente en Bolivia el número de nuevos casos confirmados por departamento. Se utiliza la serie temporal de estos casos obtenida del sitio oficial del Gobierno de Bolivia sobre el COVID-19 desde el 15 de Marzo 2020 al 6 de Julio de 2020.

2.2 Desarrollo del Modelo

2.2.1 Estimación Bayesiana

Los datos de casos nuevos apuntan al valor que R_t puede tener a la fecha. Asumiendo que el valor de R_t hoy esta relacionado su valor previo de ayer R_t−1 y para tal efecto a todos los valores, [32008Bettencourt & Ribeiro] proponen el uso de la regla de Bayes para actualizar la información disponible acerca de el verdadero valor de R_t a la fecha. Se hace uso de la siguiente forma del Teorema de Bayes [[21763Bayes & Price]]:

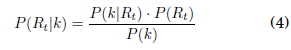
Esta ecuación expresa que, habiendo confirmado k nuevos casos, se considera que la probabilidad de R_t es igual a la probabilidad haber observado k nuevos casos dado el valor de R_t, multiplicada por la probabilidad previa P(R_t) dividida entre la probabilidad de observar k casos.

Al realizar las iteraciones: para cada nuevo día , se utiliza la probabilidad del día anterior P(R_t−1) como probabilidad previa P(R_t). Se asume que la distribución de R_t es gausiana centrada aldededor de R_t−1, de manera que

P(R_t|R_t−1)=N(R_t−1, σ) (5)

donde σ es un parámetro que se estimará luego. Aplicando al primer día:

P(R₁|k₁) ∝ P(R₁)·L(R₁|k₁) (6)

Que se interpreta como: La probabilidad de R₁ dado que se observaron k₁ casos es proporcional a la probabilidad de observar el valor R₁ multiplicado por la verosimilitud de haber observado k₁ casos dado que R_t haya adoptado el valor R₁. Bajo la misma lógica al segundo día se tiene:

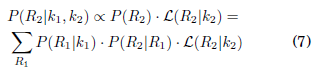
Se ha trasladado el problema a encontrar la verosimilitud.

2.2.2 Seleccionando una Función de Verosimilitud L(k_t|R_t)

La función de verosimilitud que se necesita debe estimar cuan probable es observar k casos nuevos, dado cierto valor de R_t. Dada una tasa media de recurrencia de λ nuevos casos por día, la distribución de la probabilidad de observar k nuevos casos puede modelar con una distribución de Poisson:

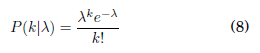
En caso de existir una sobredispersión del número de casos una distribución binomial negativa genera mejores resultados.

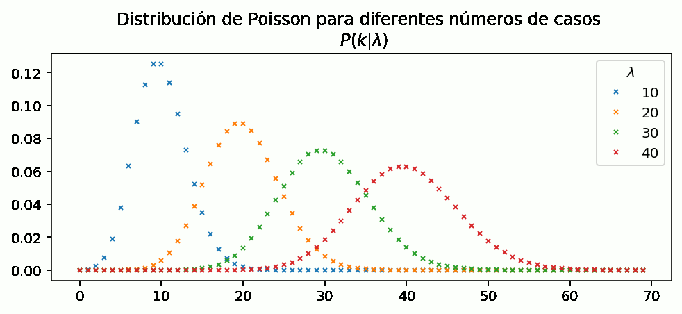
Figure 1: Se observa la coincidencia entre los picos de máxima probabilidad de las distribuciones de Poisson con sus respectivos números de casos

La distribución de Poisson modula la variabilidad del número de nuevos casos alrededor del número de casos esperado λ. Pequenñas variaciones sobre el número de nuevos casos esperados son más probables que grandes variaciones.

En el presente caso, se tiene la certeza de haber recibido k casos nuevos y se busca determinar cual era el número de casos más probable (λ). Con ese fin, se fija el número k mientras se varía el valor de λ. La función resultante de este procedimiento es la función de verosimilitud.

Por ejemplo, se observan k=20 casos nuevos, y se pretende saber cuan probable es cada λ: Se tiene P(λ_t|k_t), que esta parametrizado por λ pero se busca P(k_t|R_t) que esta parametrizado por R_t. Se requiere saber la relación entre λ y R_t

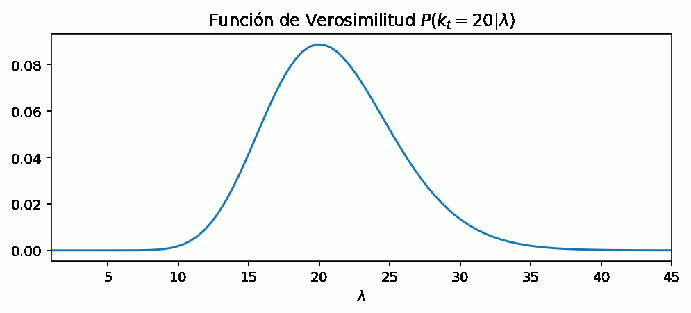
Figure 2: Si se registran k=20 casos en un día, el valor más probable al que apunta λ es 20, sin embargo otros valores son posibles. La probabilidad de que lambda sea diferente de k decae rápidamente si el número de casos se aleja de 20.

2.2.3 Conectando λ y R_t

La siguiente ecuación, derivada del trabajo de Bettencourt y Ribeiro [1] muestra una relación entre R_t y λ que se puede usar para reparametrizar la función de verosimilitud obtenida anteriormente.

λ = k_t−1e^γ(R_t−1)

(9)

En esta ecuación, γ es el recíproco del Intervalo Serial de la enfermedad (Se ha utilizado γ = 1/4 para el COVID19 [[52020Du et al.]]). El intervalo serial es el tiempo medio entre el reporte de dos casos en los cuales el segundo se ha derivado del primero. Ya que se conocen la cuenta de nuevos casos del día previo, es posible reformular la función de verosimilitud como una distribución de Poisson parametrizada al fijar k y variar R_t.

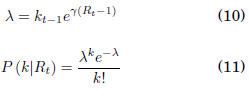
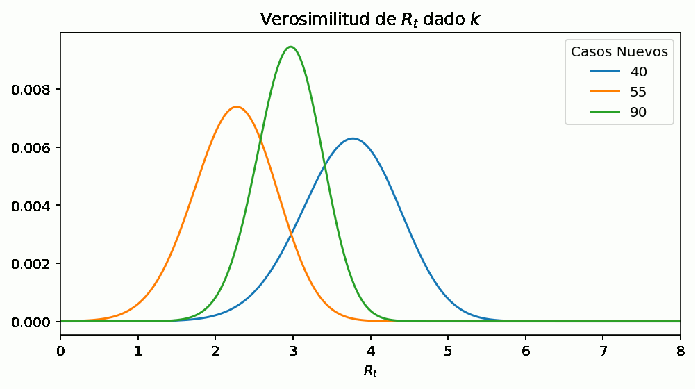
Figure 3: Se estiman valores de R_t para una serie temporal de casos k usando la función de verosimilitud. Cada día se tiene una nueva estimación de R_t. Nótese que incluso con un mayor número de nuevos casos se estima un menor valor de R_t, esto se debe a que la distribución de Poisson del primer día carece de información previa y por tanto es poco confiable, lo cual se evidencia en que la verosimilitud en el pico es inferior a los otros dos días y el ancho de la distribución es mayor. La estimación se refina en días posteriores, incrementando la verosimilitud en el pico con cada día que pasa.

2.2.4 Actualizando los valores con el Teorema de Bayes

Se multiplica la verosimilitud por la probabilidad previa (que es la verosimilitud del dia anterior) para obtener la probabilidad posterior. Esto se realiza usando el producto cumulativo de cada día consecutivo.

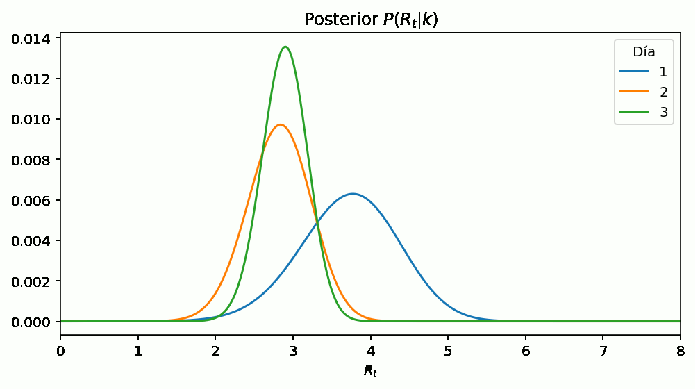
Figure 4: En el día 1, la probabilidad posterior es la misma que la del día 1 del gráfico anterior. Esto se debe a que no se tiene información previa a esa. Sin embargo, al actualizar con la información del día siguiente se aprecia un cambio, no tan marcado como en el anterior gráfico. Esto se debe a que se emplea la información de los dos días anteriores. Como la verosimilitud del día 3 esta entre las 2 previas solo se nota un pequeño desplazamiento. Lo que es más importante es que la distribución es más angosta, esto implica un incremento en la confianza sobre el valor de R_t para cada día basados en los datos del día previo.

Con estas probabilidades posteriores es posible responder para cada día preguntas importantes como: ?`Cuál es el valor más probable de R_t?

También se pueden obtener los intervalos de densidad probabilística más alta para R_t, permitiendo de esta forma crear intervalos de confianza para los valores de R_t.

Esto hace posible graficar los valores más probables de R_t y su intervalo de confianza al 95%. La gran utilidad de esta representación radica en que hace posible observar la evolución de las estimaciones realizadas a lo largo del tiempo.

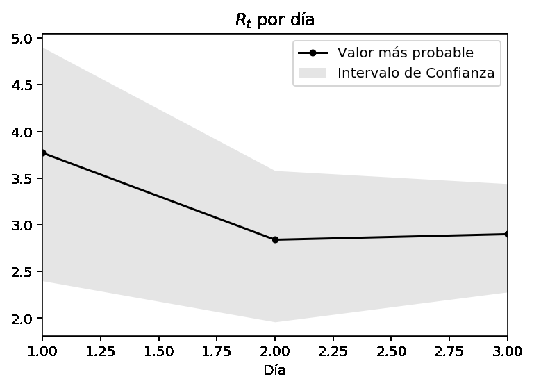
Figure 5: El valor más probable de R_t cambia en el tiempo y el intervalo de confianza se vuelve más estrecho al incrementar la certidumbre sobre el valor de R_t con cada actualización diaria del número de casos.

3 Aplicando el modelo a los datos de BOLIVIA

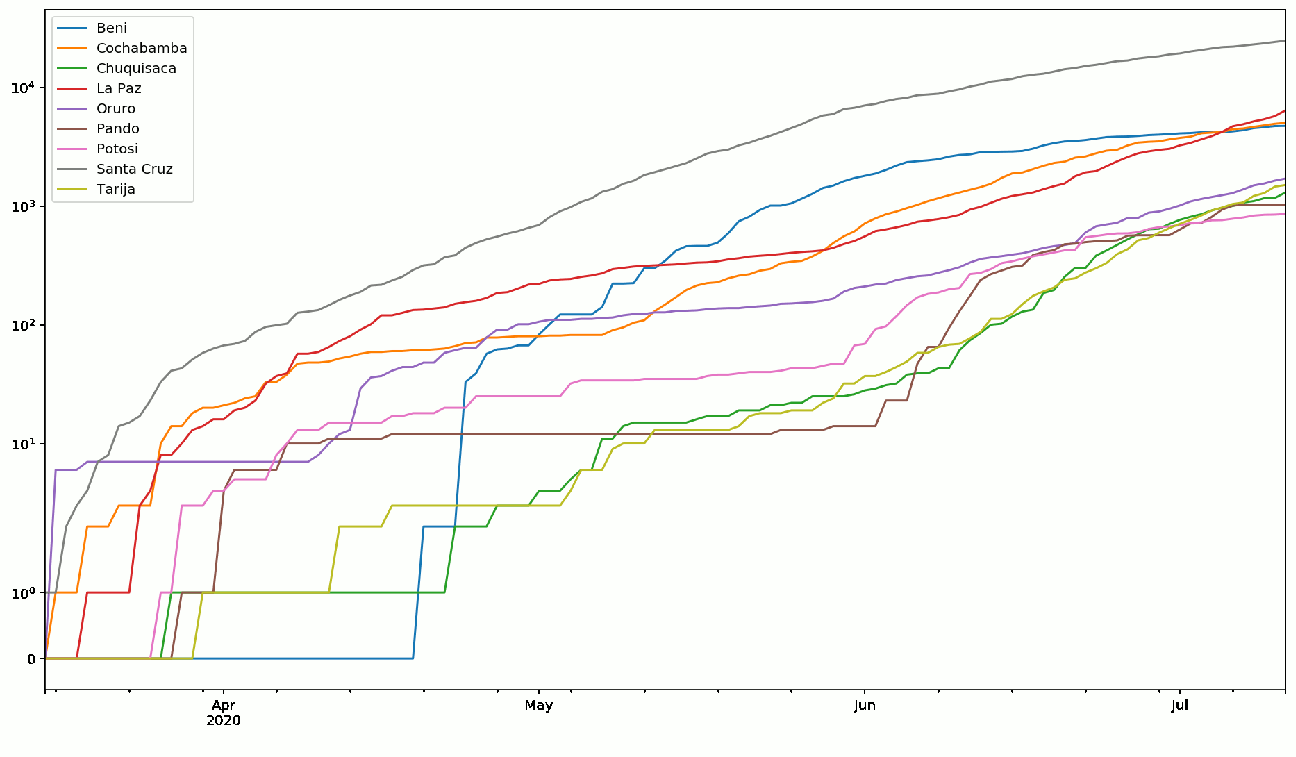
Figure 6: Datos diarios de número casos acumulados en Bolivia por departamento

3.1 Elegiendo σ para P(R_t|R_t−1)

El enfoque original simplemente selecciona la probabilidad posterior de ayer como la probabilidad previa para hoy. Aunque es intuitivo, hacerlo de ese modo no da lugar a la conjetura de que el valor de R_t posiblemente ha cambiado desde ayer. Para permitir ese cambio, se aplica ruido gausiano a la probabilidad previa con una desviación estandar σ. Para valores mayores de σ se tiene un ruido de mayor amplitud y mayor será la espectativa de cambio de R_t. Es interesante mencionar que, al aplicar ruido sobre una señal ruidosa implica que habrá un decaimiento natural de probabilidades posteriores distantes. Este enfoque calcula una serie de valores de R_t que explican todos los casos, asumiendo que R_t fluctúa una cantidad σ cada día.

Sin embargo, elegir un valor para σ es arbitrario. Se propone usar una función de máxima verosimilitud para respaldar la selección de σ.

El proceso propuesto por [112020Systrom] elije un σ que maximiza la verosimilitud de ver el número de casos k: P(k|σ). Como σ es un valor constante, lo que se intenta hacer es buscar el máximo P(k) de entre todas las opciones de σ.

Como

P(k)=P(k₀,k₁,…,k_t)=P(k₀)P(k₁)…P(k_t)

(12)

se necesita definir P(k_t). Resulta que este es el denominador en la regla de Bayes. A fin de calcularlo, se identifica que el numerador es en realidad la distribución conjunta de k and R:

P(k_t,R_t) = P(k_t|R_t)P(R_t)

(13)

Se marginaliza la distribución sobre R_t para obtener P(k_t):

De esta forma, si se suma la distribución del numerador sobre todos los valores de R_t, se obtiene P(k_t). Y como se esta calculando al mismo tiempo que la probabilidad posterior, se revisará por separado.
Como se esta buscando el valor de σ que maximiza P(k), en realidad se pretende maximizar lo siguiente:

donde t representa todos los tiempos e i representa cada departamento del país.

Como se están multiplicando varias pequeñas probabilidades entre sí, resulta conveniente (y menos conducente a errores) el tomar el log de las probabilidades y sumar los resultados. Maximizar la suma de los log de las probabilidades es equivalente a maximizar el producto de las probabilidades no-logarítmicas para cualquier σ.

3.2 Función para calcular las probabilidades posteriores

Se siguen los siguientes pasos:

Se calcula λ - la tasa estimada de llegada para el proceso de Poisson de cada día.
Se calcula la distribución de verosimilitud de cada día sobre todos los posibles valores de R_t.
Se calcula la matriz de proceso basada en el valor de σ anteriormente descrito.
Se calcula la probabilidad inicial, ya que se empieza sin una propabilidad previa al primer día.

Se itera desde el día 1 hasta el día final, con las siguientes instrucciones:

Calcular la probabilidad previa mediante aplicar ruido gausiano a la probabilidad previa del día anterior.
Aplicar la regla de Bayes mediante multiplicar esta probabilidad previa por la verosimilitud que se calculó previamente.
Dividir entre la probabilidad de los datos observados (aquí también se aplica la regla de Bayes).

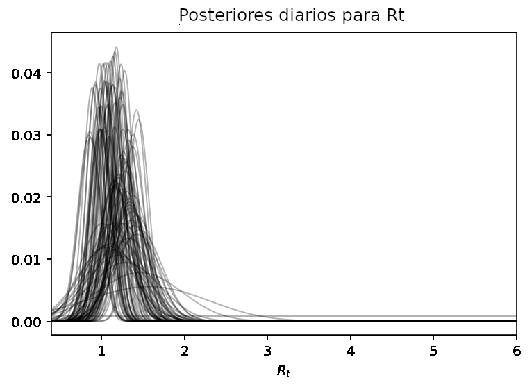
Figure 7: Distribuciones posteriores de todos los días graficadas simultáneamente. Las primeras son bastante anchas ya que se tiene poca confiabilidad pero se vuelven cada vez más angostas ya que la confiabilidad de que incluyan el valor verdadero de R_t incrementa.

3.3 Graficando la evolución temporal con intervalos de confianza

Como los resultados deben incluir incertidumbre, resulta sumamente útil poder visualizar los valores más probables junto con sus intervalos de mayor densidad.

Table 2: Valores de Máxima verosimilitud con intervalos de mayor densidad probabilística que estiman el valor de R_t para datos de Bolivia.

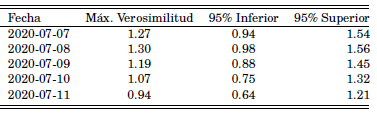
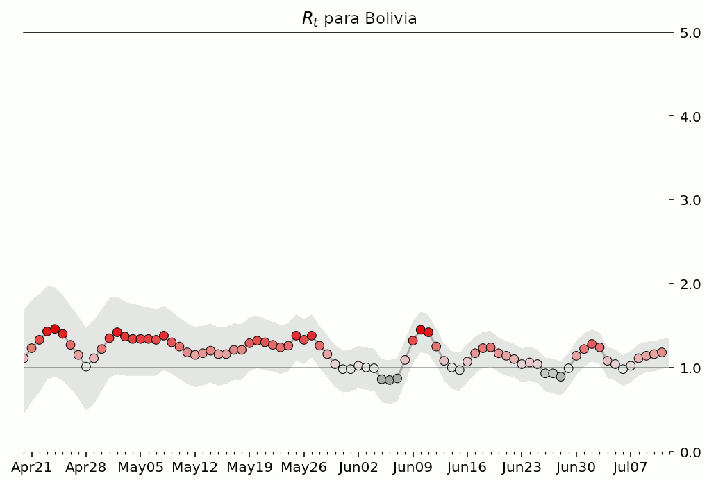
Figure 8: Evolución temporal de R_t para Bolivia. El valor oscila entre 1 y 2, manteniéndose la mayor parte del tiempo por debajo de los valores R₀ reportados por [4], posiblemente como consecuencia de las restriciones a la circulación impuestas durante los últimos meses (Marzo 2020 - Julio 2020)

3.4 Eligiendo un σ óptimo

En la sección previa se mostró como obtener un valor de σ, pero en el cálculo se asumió un valor arbitrario. Ahora que es posible evaluar cada departamento con cualquier sigma, se tienen todas herramientas para encontrar el mejor σ. Se mencionó previamente que se encontraría el valor de σ que maximiza la verosimilitud de las distribuciones P(k) de los datos. Para evitar hacer un ajuste muy parcializado hacia un departamento en particular, se va a elegir el sigma que maximice P(k) en el conjunto de todos los departamentos. Para hacerlo, se añaden todos los logaritmos de las verosimilitudes por departamento para cada valor de σ y entre esos se elige al máximo.

3.5 Resultados por Departamento

Dado que se han seleccionado los σ's óptimos, se toma el posterior precalculado correspondiente a ese valor de σ para cada departamento. Se calcula el intervalo de densidad más alta (95%) y también el valor más probable.

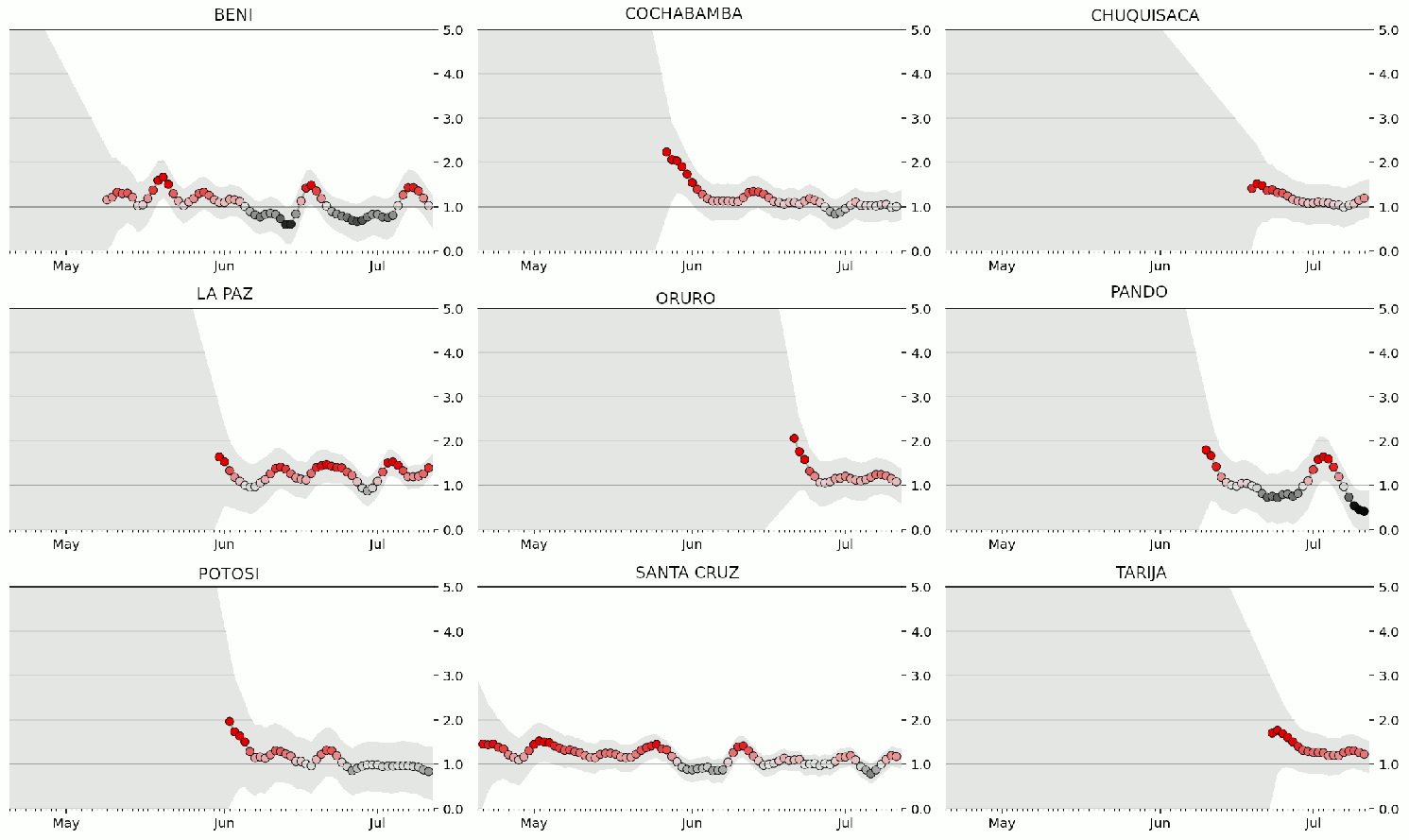
Figure 9: Estimaciones de R_t para los nueve departamentos de Bolivia, basadas en el reporte diario de número de casos por departamento. En departamentos con mayor número de casos, el intervalo de confianza de R_t converge más rapidamente, permitiendo al algoritmo imprimir el valor estimado de R_t. Los intervalos de confianza se van haciendo más estrechos al incrementar el número de casos. Se aprecia que R_t en la mayoría de los departamentos, a lo largo de los últimos 30 días, posee un valor ligeramente superior a 1. Lo cual indica un incremento lento en el número de casos, comparado con el incremento que se podría esperar si R_t tuviera alguno de los valores del intervalo reportado en la Tabla 1 para el COVID-19

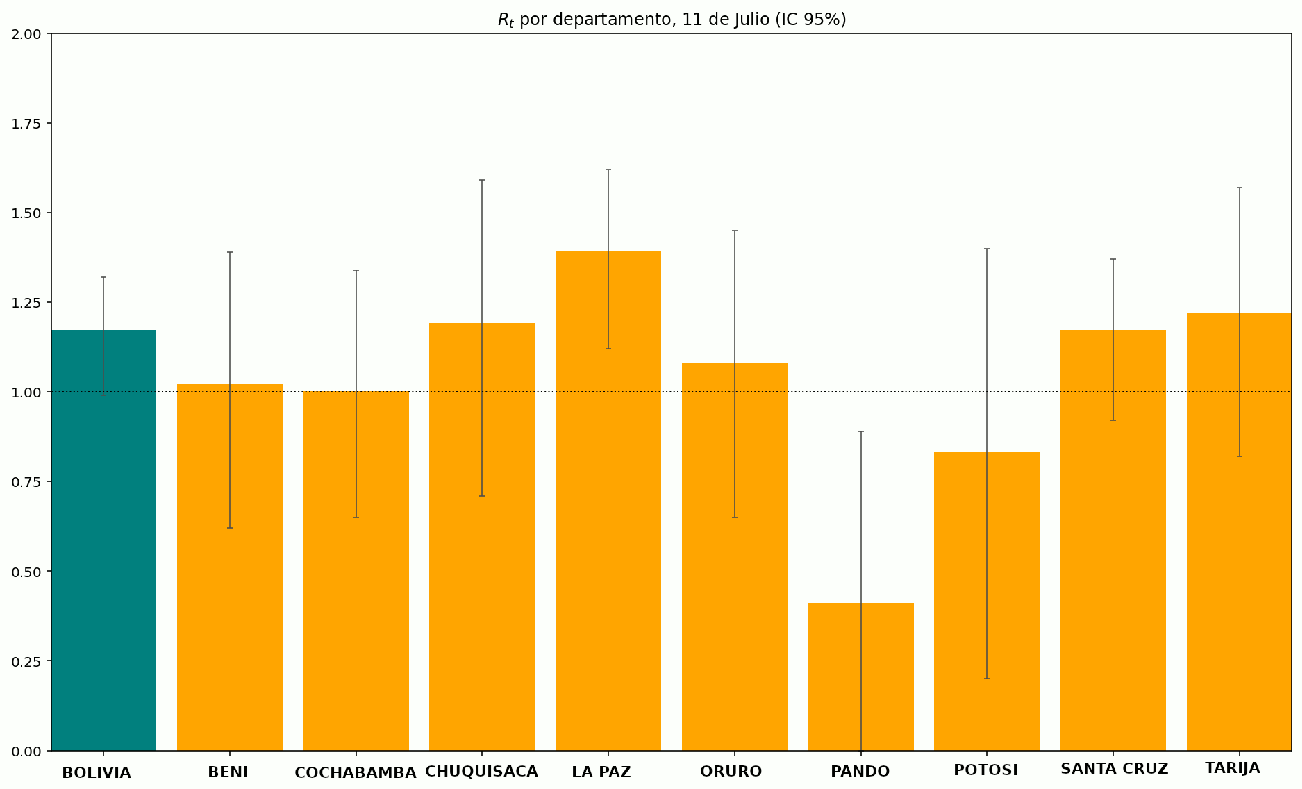
Figure 10: Se comparan las estimaciones de R_t al 11 de Julio de 2020 para cada departamento y para Bolivia. Los intervalos de confianza al 95% están representados por barras de error.

4 Proyecciones usando el modelo SIR

Para demostrar el valor práctico de estimar R_t se realiza una proyección del número de casos usando el valor de R_t estimado a la fecha como parámetro en el modelo SIR. La intención de esta proyección es ser una prueba de concepto para otras aplicaciones de la estimación de R_t que van más allá de realizar un diagnóstico de la situación presente. Dependiendo de las circunstancias, es posible aplicar otros modelos más complejos que se beneficien de un valor efectivo del número de reproducción.

Table 3: Variables usadas para realizar la proyección con el modelo SIR

Se obtuvo la tasa de contacto de la estimación previamente realizada de R_t para Bolivia y luego se realizó la integración del modelo SIR sobre 300 días a partir de la fecha (11 de Julio de 2020)

Table 4: Valores obtenidos del modelo SIR para el caso más probable

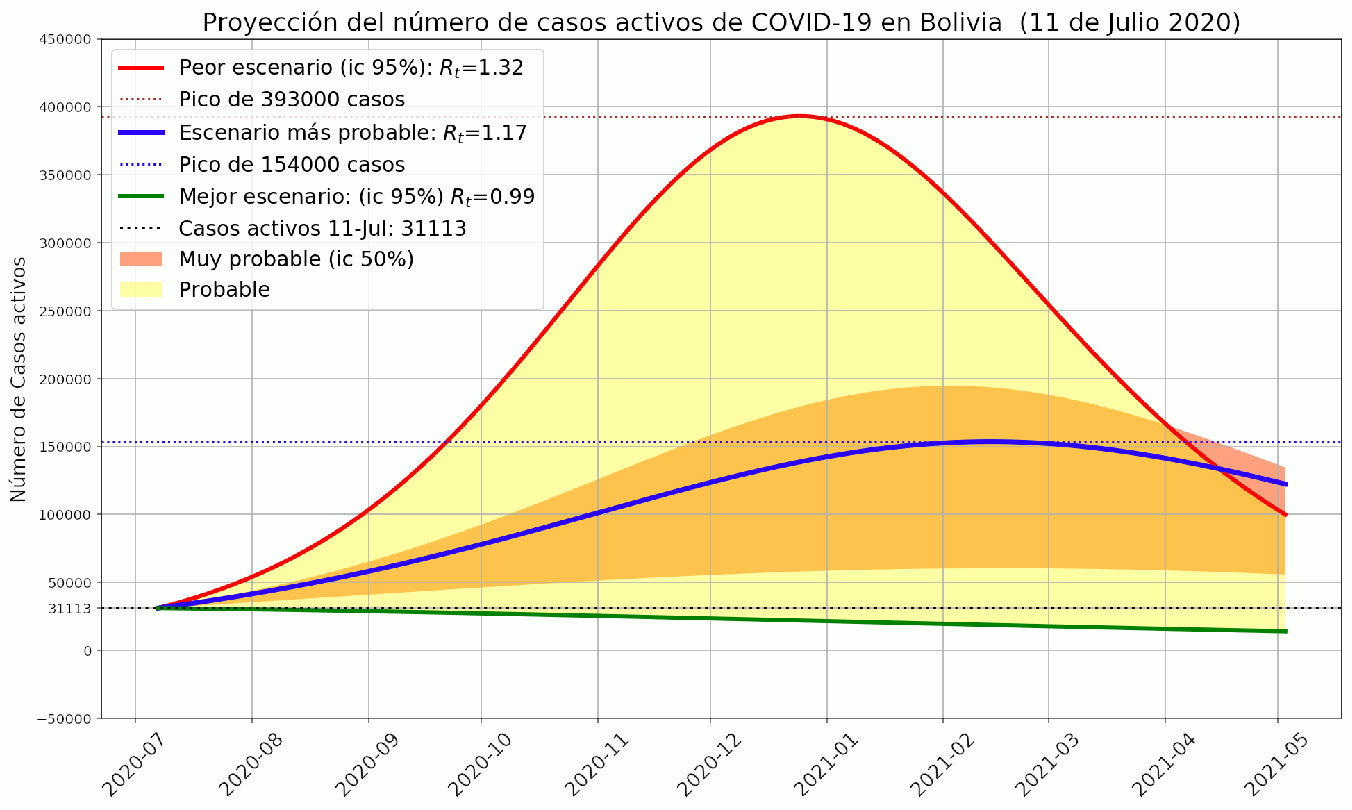
Figure 11: En este gráfico se muestran 5 proyecciones distintas del número de casos activos. El escenario más probable proviene de la estimación de R_t que posee la máxima verosimilitud. El mejor y peor escenario provienen de los valores límite del intervalo de confianza de R_t al 95%. También se incluyeron otras dos proyecciones para los valores límite del intervalo de confianza al 50%, que aparecen delimitando el área marcada como Muy probable. Estas proyecciones muestran los diferentes plazos para alcanzar pico de casos activos, el más próximo (al 11 de Julio de 2020) es un pico que ya debería haberse alcanzado en días previos, y el más alejado es un pico en el mes de Febrero de 2021. Evidentemente este resultado es trivial, dado que comprende un intervalo de varios meses.

En el contexto de una proyección a largo plazo (300 días), el escenario más probable es solo una guía y no debería considerarse como el valor representantivo del reporte. El peor escenario es el que resulta más util para establecer una respuesta estratégica ante la pandemia. El caso nacional esta lejos de ser la aplicación óptima de este modelo. Más adelante se exponen los motivos para evitar este tipo de aplicación del modelo y se sugieren algunos escenarios ideales.

5 DISCUSIÓN

5.1 Acerca de la estimación de R_t

El enfoque Bayesiano de estimación de R_t permite hacer uso de los datos disponibles para monitorear la evolución de este parámetro. El registro de sus sucesivos valores en el tiempo muestra variaciones que pueden ser identificadas como variaciones en la tasa de contagios o en la tasa de pruebas administradas, registros históricos de actividades de rastrillaje, eventos masivos o variaciones en las regulaciones de circulación pueden ser usados para identificar el origen de las variciones de R_t.

Es sumamente importante hacer notar que existe un lapso de tiempo entre el momento en que se produce el contagio y el momento en que se registra como caso positivo, por tanto debe existir un retraso entre las actividades que puedan modificar R_t y el registro de la modificación de su valor. Este retraso tendrá como pricipales componentes: el intervalo entre el contagio, la aparición de síntomas y la atención médica, además del tiempo de procesamiento de la prueba, en casos rurales se especula que estos tiempos pueden ser significativamente mayores debido a la necesidad del traslado del paciente o de la muestra. Por otro lado, los datos disponibles no especifican el tipo de prueba utilizada para la confirmación del caso, dada la administración de pruebas rápidas de COVID-19 se debe advertir que el retraso de las variaciones de R_t puede verse afectado, esto implica una pérdida de resolución temporal. Sin embargo, las tendencias a plazos más largos que la diferencia entre pruebas rápidas y pruebas regulares se mantienen inalteradas, en otras palabras, puede que los picos sean menos pronunciados o más extendidos en el tiempo.

Es importante mencionar que en el caso de Bolivia la cantidad de pruebas por habitante es todavía baja comparada con otros países, esto añade incerteza a los datos manejados. Dado que uno de los principales intereses en el monitoreo de R_t es el de evaluar los efectos de cambios en restricciones sociales (circulación, distanciamiento social y otros), y que a pesar de la mayor incertidumbre, las tendencias inducidas por estas restricciones son capaces de reflejarse proporcionalmente en los casos que se registran, por tanto no se puede descartar R_t en base a una incertidumbre respecto al número de casos totales o a la proporción de casos registrados. Objeciones a este último argumento podrían ser que de alguna forma las restricciones no se apliquen equitativamente a toda la población, o que de alguna forma las pruebas se administren sistemáticamente a cierta parte de la población y no a otra.

Ya que diferentes regiones y ciudades tienen diferentes formas de implementar las restricciones, además de diferentes variables ambientales, es necesario recomendar la estimación de R_t a la escala más pequeña posible. Idealmente a nivel de ciudades o incluso barrios, si es que existe un gran número casos. A escala nacional su uso es contraproducente ya que cada región suele poseer diferente número de habitantes, diferente proporción inicial de casos y diferente densidad poblacional, todos factores que afectan fuertemente las estimaciones de R_t y el número de casos futuros. Dado que R_t depende fuertemente del número de casos activos, una estimación nacional de R_t va a estar desproporcionadamente influenciada por las regiones con mayor número de casos totales, independientemente de otros factores, lo cual puede generar una perspectiva errónea de la situación para cada región.

5.2 Hallazgos en los datos analizados

Las Figuras 9 y 10 muestran valores de R_t que inicialmente convergen hacia 1 y oscilan por encima del mismo. Lo cual indica una situación en la cual los casos nuevos continúan incrementando, pero a un ritmo inferior al que se podría esperar considerando que el mínimo R₀ de la literatura disponible a la fecha es de 1.5 [[82020Liu et al.Liu, Gayle, Wilder-Smith, & Rocklöv]]. Esto implica que las restricciones a la circulación que han estado vigentes en los primeros meses de la pandemia de COVID19 estan teniendo el efecto de reducir los contagios y mantener el número de casos activos dentro de un rango pero no lo suficiente como para que empiece a reducir.

Los intervalos de confianza revelan que en varios departamentos, especialmente Pando y Potosí, existe una elevada incertidumbre en el valor de R_t. Dos factores contibuyen a esto: La baja cantidad de casos y la gran variabilidad en el número de casos nuevos que se reportan. Las causas de esa variabilidad pueden ser demográficas (elevada poblacion con bajo acceso a centros de salud capaces de realizar pruebas) o técnicas (falta de suficiente número de pruebas para ser administradas, falta de suficientes laboratorios capaces de analizar el volumen de pruebas realizado, o falta de personal de laboratorio suficiente).

5.3 Acerca de la proyección usando el modelo SIR

Se justifica el uso del modelo SIR para la proyección del número de casos activos bajo los siguientes argumentos:

El modelo SIR es simple: sus parámetros son posibles de medir y su interpretación inmediata esta al alcance de los profesionales de la salud, de los encargados de la administración pública y puede hacerse accesible a la población en general.
Existen numerosas fuentes de referencia, y mucha teoría epidemiológica desarrollada alrededor del modelo SIR y sus variantes, haciendo que la progresión hacia modelos similares pero más sofisticados sea natural y relativamente libre de complicaciones.
Modelos derivados no se especializan tanto en enfermedades emergentes como el modelo SIR. Ya que la gran mayoría de la población todavía es suceptible (más del 99%, a la fecha).

5.4 Limitaciones del modelo SIR

El modelo SIR asume que todo individuo es capaz de interactuar con todo otro individuo de la población. Tambien asume que la población es constante (no toma en cuenta cambios en la población resultado de nacimientos, fallecimientos o migración). También asume que los recuperados no vuelven a infectarse. No toma en cuenta variaciones la tasa de recuperación relacionadas con características como edad o sexo. Por último, tampoco toma en cuenta la variación de los parámetros biológicos de virus (mutaciones) que podrían modificar su transmisibilidad o la progresión temporal de la enfermedad en el infectado.

Como los intervalos de tiempo que se pretenden modelar son meses, la variación de la población que se puede esperar debida a nacimientos y fallecimientos es pequeña y es razonable no tomarla en cuenta en el modelo. La migración esta fuertemente restringida asi que también se puede despreciar. A la fecha todavía no se han confirmado casos de recuperados que vuelvan a infectarse y esparcir la enfermedad, si bien no se conoce si la inmunidad es permanente, el tiempo de inmunidad parece ser lo suficientemente largo como para que no se necesite modificar el modelo si es aplicado en el intervalo de meses, tal y como se pretende. Se afronta el problema de las diferencias en las tasas de recuperación entre diferentes grupos etarios de la población mediante usar un valor promedio de toda la población, ya que se trata de una cantidad grande de casos esta estimación es razonble. En cuanto a las mutaciones del virus, se puede esperar que el virus cambie a lo largo de años o meses, si se realizan proyecciones a días o semanas es razonable esperar que los parámetros biológicos del virus no hayan cambiado apreciablemente. Esto último subraya la importancia evitar las proyecciones de largo y mediano plazo.

La última consideración respecto a limitaciones del modelo SIR se refiere la posibilidad de un individuo de interactuar con todos los otros individuos de la población. Dadas las restricciones vigentes a viajes es posible decir que cada ciudad esta aislada de las otras, esto hace que el modelo SIR no sea estrictamente válido para el caso nacional, o para los casos departamentales. Esta última consideración no es válida solo para este modelo, sino que es válida para todo otro modelo que no considere que la población esta acumulada en compartimentos geográficos. La solución ideal a esto es aplicar el modelo SIR a cada localidad, determinando previamente el R_t local.

5.5 Otras consideraciones

La propagación del virus también depende de factores sociales, que solo pueden ser tomados en cuenta invocando múltiples variables, esto añade considerablemente a la complejidad de cualquier modelo que intente describirlo. Tambien se puede argumentar que la percepción social sobre la seriedad de la propagación afecta la propia propagación, ese es un indicador de la no-linealidad del fenómeno observado. Otros fenómenos no lineales, por ejemplo el clima, no suelen pronosticarse a largo o incluso mediano plazo.

6 CONCLUSIONES

Los datos analizados a través del modelo demuestran una tendencia de R_t acorde a las circunstancias presentes y además sugieren dificultades que pudieran estar atravesando algunos departamentos. Lo cual manifiesta la importancia de vigilar esta métrica. Debido a que R_t depende de factores biológicos, sociales y ambientales que son distintos en cada núcleo poblacional. Se debería estimar el valor de R_t para cada núcleo poblacional que tenga suficientes casos para realizar la estimación. A raíz de los posibles cambios poblacionales por nacimientos y fallecimientos, la incertidumbre acerca de la permanencia en el estado inmune y la posibilidad de mutación del virus, no es recomentable hacer proyecciones a largo plazo. Debido a las restriciones a los viajes entre ciudades, es recomendable que el modelo SIR se aplique a núcleos poblacionales y no a grupos de ciudades o a paises enteros. La naturaleza social de la propagación del virus limita seriamente la posibilidad de hacer pronósticos muy extendidos en el tiempo sobre número de casos.

6.1 Consideraciones finales

Se ha mostrado como prueba de concepto que es posible hacer una proyección del pico de casos a nivel nacional con las herramientas expuestas en este artículo, pero solo se pretende su análisis a nivel ilustrativo, para luego ser reproducido a escala de núcleos urbanos. Ante la importancia de una interpretación clara, se hace necesario señalar algunos casos ideales de aplicación de estos métodos y modelos:

Es ideal usar la estimación de R_t para evaluar el efecto de un cambio de las restricciones de la cuarentena. Se debe tomar en cuenta un retraso hasta que el cambio se vea reflejado en el valor de R_t.
Es ideal usar el modelo SIR en conjunción con la estimación local de R_t para determinar cuanto tiempo se tiene hasta que el número de casos rebase la capacidad hospitalaria local.

Se agradece muy profusamente a Kevin Systrom, quien inspiró la producción de este artículo y que contribuyó en gran medida al mismo a través de código en python.

Conflicto de intereses El autor declara que no hay conflicto de intereses con respecto a la publicación de éste documento.

References

[12020Alberti & Faranda]

Alberti, T. & Faranda, D. 2020, Commun Nonlinear Sci Numer Simul, 90, 105372 [ Links ]

[21763Bayes & Price]

Bayes, T. & Price, R. 1763, Philosophical Transactions of the Royal Society of London, 53, 370 [ Links ]

[32008Bettencourt & Ribeiro]

Bettencourt, L. M. A. & Ribeiro, R. M. 2008, PLOS ONE, 3 (5), e2185 [ Links ]

[42019Delamater et al.]

Delamater, P. et al. 2019, Emerging Infectious Diseases, 25 [ Links ]

[52020Du et al.]

Du, Z. et al. 2020, Emerging Infectious Diseases, 26, 1341 [ Links ]