A. ARTÍCULOS

 

Estimación de la probabilidad de contagio de covid-19 por aerosoles en ambientes cerrados: Aplicaciones a casos en la ciudad de La Paz, Bolivia

 

Estimation of the probability of contagion of covid-19 by aerosols in closed environments: Applications to cases in the city of La Paz, Bolivia

 

 

Fernando Velarde, Rubén Mamani-Paco, & Marcos Andrade-Flores^†
†mandrade@fiumsa.edu.bo
Instituto de Investigaciones Físicas, Universidad Mayor de San Andrés Campus Universitario, c. 27 Cota-Cota, Casilla de Correos 8635 La Paz - Bolivia
(Recibido 30 de noviembre de 2020; aceptado 20 de diciembre de 2020)

 

 

---

Resumen

Desde la llegada del coronavirus SARS-CoV-2 las entidades de salud publicaron recomendaciones para evitar el contagio de la COVID-19 asociada a dicho virus. Las más importantes están relacionadas con evitar el posible contagio a través de superficies contaminadas (fómites) y la deposición de gotículas de saliva en ojos, nariz o boca. Evidencia observacional y teórica, sin embargo, sugiere que en ambientes cerrados la forma más importante de contagio está relacionada a aerosoles respiratorios infecciosos. En este trabajo se usa un modelo matemático para estimar la probabilidad de contagio por estos aerosoles en ambientes cerrados. Este modelo se aplica a tres casos: un aula de clases, un teatro y vehículos de transporte público de la ciudad de La Paz, Bolivia. Los resultados muestran que la probabilidad de contagio de la COVID-19 depende fuertemente del tiempo de exposición (duración de los eventos) y la ventilación de los ambientes. A mayor duración y menor ventilación mayor la probabilidad de contagio. Adicionalmente, se midió la concentración de dióxido de carbono como un proxy de la calidad de aire, en términos de la concentración de aerosoles, y para establecer niveles de ventilación de algunos de los ambientes cerrados estudiados. Los resultados del modelo aplicado al aula de clases indican que la probabilidad de contagio en caso de una clase de dos horas y que el instructor fuera un portador asintomático es del orden de 10%, mientras que para el caso del teatro la probabilidad de contagio es del orden del 25% para la función estudiada. Finalmente, en el caso de los minibuses, el medio de transporte público más usado en Bolivia, la probabilidad de contagio para viajes de 60 minutos, oscila entre 19% y 97% dependiendo del número de pasajeros que estén infectados (entre uno a seis en este estudio) y, fundamentalmente, de la ventilación que depende, a su vez, de si las ventanas del vehículo estén cerradas o abiertas. La conclusión más importante del estudio indica que ventilar ambientes es la acción más importante para reducir el riesgo de contagio de la COVID-19 en ambientes cerrados.

Descriptores: Aerosoles — enfermedades — probabilidad de contagio.

Código(s) PACS: 42.68.Jg, 87.19.xd, 02.50.-r

---

Abstract

Since the arrival of the SARS-CoV-2 coronavirus, health entities published recommenda-tions to avoid the spread of COVID-19. The most important ones are related to avoiding pos-sible contagion through contaminated surfaces (fomites) and the deposition of saliva droplets in the eyes, nose or mouth. However, observational and theoretical evidence suggests that in closed environments the most important form of contagion is related to infectious respiratory aerosols. In this work a mathematical model is used to estimate the probability of contagion by these aerosols in closed environments. This model is applied to three cases: a classroom, a theater, and public transportation vehicles in the city of La Paz, Bolivia. The results showed that the probability of contagion of COVID-19 strongly depends on the exposure time (duration of events) and the ventilation of the environments. The longer the duration of an event and the poorer the ventilation of the environment, the greater the probability of contagion. Additionally, carbón dioxide concentration was measured as a proxy for indoor air quality, in terms of aerosol concentration, and to establish ventilation levéis in some of the closed environments studied. The results of the model applied to the classroom indicate that the probability of contagion in the case of a two-hour class and an asymptomatic carrier (instructor) is of the order of 10%, while in the case of the theater the probability of contagion is of the order of 25% for the studied event. Finally, in the case of minibuses, the most used means of public transport in Bolivia, the probability of contagion for 60-minute trips ranges between 19% and 97% depending on the number of passengers who are infected (between one to six in this study) and, fundamentally, on the ventilation that depends on whether the windows of the vehicle are closed or open.

Subject headings: Aerosols — diseases — probability of contagion.

---

 

 

1. INTRODUCCIÓN

En enero 31, 2020 la Organización Mundial de la Salud (OMS) declaró al brote del nuevo coronavirus denominado SARS-CoV-2 (severe acute respiratory syndrome coronavirus 2) una emergencia pública de importancia internacional, el nivel más alto de alarma de esta institución, y en marzo 11 declaró al COVID-19 (coronavirus disease 2019) una pandemia. Desde entonces se ha avanzado mucho en cuanto al entendimiento de las forma de contagio de esta enfermedad.

Existen diferentes maneras en la que el virus puede ser transmitido de persona a persona: a través de deposición directa o indirecta por medio de objetos (fómites), y a través del aire por medio de gotículas (pequeñas gotas de saliva que se producen al hablar, estornudar o toser) y aerosoles (Zhang et al. 2020). Las primeras recomendaciones estuvieron asociadas a evitar el contagio por: 1) fómites, a través del lavado constante de manos con agua y jabón, y 2) por deposición de gotículas en los ojos, nariz y boca, a través del uso de barbijos y de mantener una separación entre personas del orden de 2 m (distanciamiento social). En este último caso se consideró convencionalmente que las gotículas tienen un tamaño aerodinámico mayor a 5 /im ¹ y que caen al suelo rápidamente después de ser expulsadas por la boca o nariz (Zhang et al. 2020).

A pesar que estudios previos indicaron que los aerosoles juegan un rol importante en la transmisión de virus respiratorios, como la influenza (Zhang et al. 2020), al principio de la pandemia no se señaló la importancia de este medio de transmisión para el SARS-CoV-2². Más tarde, sin embargo, se enfatizó el rol de la propagación aérea de la COVID-19 (Morawska & Milton 2020) a través de aerosoles (referidas en éste estudio como microgotas con diámetros aerodinámicos menores a las gotículas) a distancias de pocos metros, es decir a distancias típicas de ambientes en casas, departamentos, oficinas e inclusive del transporte público.

La importancia de los aerosoles está relacionada fundamentalmente a dos causas: i) partículas menores a 100 /im pueden quedar suspendidas en el aire por tiempos entre minutos a horas en ambientes cerrados con poca ventilación (Yang & Marr 2011), y ii) el número de partículas emitidas al hablar, estornudar o toser tiene un pico alrededor de 1 /im y es alrededor de dos órdenes de magnitud mayor al número de gotículas cuya concentración tiene un pico relativo entre 100 y 200 /im (Johnson et al. 2011). Esto implica que las gotículas caen al suelo rápidamente al ser expulsadas mientras que los aerosoles se quedan flotando entre minutos a horas. Adicionalmente, las gotículas de saliva con aerosoles en forma sólida dentro de las mismas son expulsadas de la boca o nariz a una humedad relativa (HR) cercana al 100% y una vez en el ambiente, típicamente con valores de HR mucho menores, reducen su volumen hasta alcanzar equilibrio termodinámico (Mikhailov et al. 2004). Estos dos procesos cambian la distribución de tamaños de partículas dejando el máximo número de partículas por debajo de 20 ¡im al cabo de minutos (Yang & Marr 2011). El resultado son partículas inhalables que pueden permanecer flotando en el aire, especialmente en ambientes cerrados, por un tiempo suficiente largo como para contribuir a la transmisión de enfermedades como la COVID-19, si estas son aerosoles respiratorios infecciosos que transportan copias del SARS-CoV-2. Existe abundante evidencia que sugiere que esta manera de transmisión es mucho más importante que por fómites o gotículas (Harvey et al. 2021).

Eventos de supercontagio bien documentados, como el reportado en Miller et al. (2020), sugieren fuertemente que la vía más probable de contagio son los aerosoles. En el mencionado caso 52 personas, de 60 presentes en un ambiente cerrado, se contagian en aproximadamente 2.5 horas a partir de un solo caso. Las medidas de bioseguridad como lavado de manos y distanciamiento social fueron seguidas por las personas involucradas por lo que no hay evidencia que la transmisión se haya dado a través de fómites o por gotículas siguiendo trayectorias balísticas. Dada la pobre ventilación del ambiente, la forma más plausible de contagio fue a través de los aerosoles (Miller et al. 2020).

Siguiendo la línea de investigación de transmisión del virus por vía aérea, el objetivo de este estudio es estimar la probabilidad de contagio de COVID-19 por aerosoles en ambientes cerrados de la ciudad de La Paz, Bolivia, empleando el modelo propuesto por Miller et al. (2020) y puesto en línea con acceso libre por José Jiménez y su grupo de trabajo³. Se aplica el mismo a tres ambientes de uso masivo: un aula de clases de la Universidad Mayor de San Andrés, un teatro de la ciudad de La Paz y varios casos particulares de transporte público. Se espera así proporcionar una guía para que tanto autoridades de salud como la población en general puedan tomar medidas preventivas en el caso de realizar eventos en ambientes cerrados.

 

2. DEFINICIÓN DE PARÁMETROS EMPLEADOS POR EL MODELO

El modelo empleado se basa principalmente en resultados descritos en Miller et al. (2020); Buonanno et al. (2020). El mismo fue desarrollado en base a trabajos de Wells (1955) y Riley et al. (1978) a través de una expresión analítica conocida como la ecuación de Wells-Riley. Diferentes aproximaciones basadas en esta expresión han sido usadas en diferentes estudios de análisis de riesgos para la salud (por ejemplo, Gammaitoni & Nucci (1997); Knibbs et al. (2011)).

El modelo permite estimar la probabilidad de contagio del SARS-CoV-2, por transmisión aérea a través de aerosoles atmosféricos, de personas sanas que se encuentran en un ambiente cerrado junto con personas contagiadas bajo varias premisas. Entre las más destacadas tenemos: i) no hay contacto físico entre las personas presentes en el ambiente, ii) todos mantienen la distancia recomendada, ii) no tosen ni estornudan, y iv) los aerosoles respiratorios infecciosos se distribuyen de manera uniforme en el ambiente. A continuación se describen los parámetros más relevantes usados por el modelo.

2.1.  Carga viral emitida

Tanto el lugar del tracto respiratorio donde se originan los aerosoles así como la distribución de tamaño y número de partículas emitidas son factores importantes para entender el transporte de los virus por el aire a través de los aerosoles (Morawska et al. 2009). Estos parámetros, sin embargo, son difíciles de medir. La aproximación Wells-Riley ofrece una gran ventaja ya que resume todos estos procesos en un sólo parámetro denominado "quantum" que representa la mínima dosis que causa infección, evitando de ésta manera representar explícitamente los procesos de generación y emisión de aerosoles en la persona infectada. Por definición, un quantum es la dosis necesaria de aerosoles infecciosos requeridos para infectar al 63% de la población susceptible (Wells 1955; Buonanno et al. 2020). Buonanno et al. (2020) estimaron la carga viral del SARS-CoV-2 emitida en aerosoles por personas infectadas bajo la hipótesis de que la carga viral en el esputo de la boca es la misma a la carga viral de los aerosoles emitidos y que entre ellos existe un balance de masa. En este estudio, la carga viral emitida es expresada en términos de la tasa de emisión de quanta (Eq) la cual es función de la carga viral en la boca, el tipo de actividad (como hablar, cantar, toser, etc.), la tasa de inhalación, y el nivel de actividad física (como descansar, caminar, etc.). En la tabla 1 se muestran los valores usados en el presente estudio.

2.2.  Tasa de inhalación

La tasa de inhalación se refiere al volumen de aire transportado por los pulmones durante una inhalación/exhalación por unidad de tiempo y se calcula multiplicando el número de respiraciones de una persona por el volumen tidal o corriente en una unidad de tiempo (Madueño et al. 2019). La tasa de inhalación es una variable compleja de determinar ya que depende de factores tanto fisiológicos (por ejemplo, edad y sexo) como de la actividad que la persona desarrolla (como caminar o cantar) además de otros factores como la altura sobre el nivel del mar (presión atmosférica) y el tiempo en el cual la persona realiza la actividad (Madueño et al. 2019).

TABLA 1

Carga viral emitida por una persona infectada con-sars-cov-2 en términos de tasa de emisión de quanta (de buonnano et al, 2020)

 

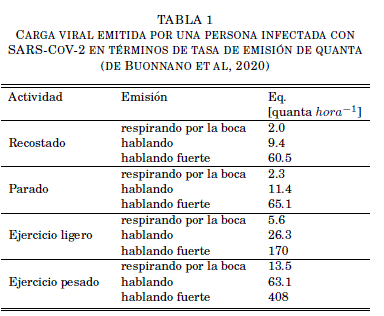
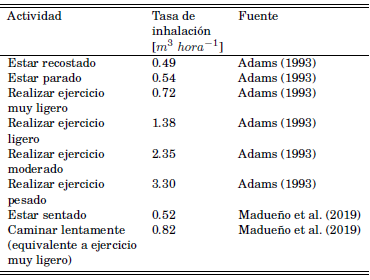
Adams (1993) determinó experimentalmente la tasa de inhalación para diferentes actividades. Estos valores fueron estimados para condiciones de nivel del mar las cuales son diferentes para las condiciones de la ciudad de La Paz, principalmente porque la densidad del aire es menor. (Madueño et al. 2020) realizaron medidas de tasa de inhalación en la ciudad de La Paz para actividades involucradas en sus objetivos. La tabla 2 muestra los valores de tasa de inhalación usados en el presente estudio. En este trabajo, la tasa de inhalación se refiere tanto a la persona infectada como a la persona susceptible. La tasa de inhalación para la persona infectada es tomada en cuenta a través de los quanta emitidos por esta. En este sentido, la tasa de inhalación es un factor importante en los cálculos referentes a la probabilidad de infección de las personas susceptibles.

2.3. Decaimiento de la infectividad del virus en aerosoles

La infectividad del virus en aerosoles y superficies depende de las condiciones ambientales, siendo la radiación solar, en particular la radiación ultravioleta (RUV), la temperatura y la humedad ambiente los factores más relevantes (Dabisch et al. 2020). En ambientes abiertos, la RUV y la temperatura tienen mayor influencia en el decaimiento de la infectividad del virus comparada con la humedad. Sin embargo, en ambientes cerrados la RUV es muy baja por lo que la temperatura y la humedad del ambiente son los factores más importantes. Dabisch et al. (2020), proponen un modelo para calcular el decaimiento de la infectividad del virus. El mismo fue estimado en 0.71 horar¹ para un ambiente cerrado con una temperatura y humedad relativa del orden de 20°C y 40%, respectivamente.

TABLA 2

Tasas de inhalación promedio para hombres y mujeres entre 21 y 30 años de edad.

2.4. Deposición de aerosoles

El modelo solamente toma en cuenta la deposición seca de los aerosoles, la cual en espacios cerrados depende principalmente del tamaño del aerosol. Como se indicó anteriormente, se consideran aerosoles en el rango de diámetros aerodinámicos entre 1 y 5 /im para lo cual la deposición es determinada como la tasa entre la velocidad de sedimentación (1.0 x 10~⁴m/s) y la altura a la cual son emitidos al ambiente (típicamente 1.5 m) dando un valor promedio de 0.24 hora-¹ (Buonanno et al. 2020).

2.5. Eficiencia de filtrado de aerosoles por barbijos

El principal motivo de usar barbijos es evitar la inhalación de aerosoles infecciosos y su subsecuente exhalación y diseminación. En el mercado existen diferentes tipos de barbijos los cuales difieren principalmente en la eficiencia de filtrado de aerosoles y su ajuste al rostro. Desde el punto de vista de modelar la transmisión del virus se debe tomar en cuenta tanto la eficiencia de filtrado de aerosoles emitidos por la persona infectada como la eficiencia de filtrado de aerosoles del aire respirado por la persona susceptible. Para el rango de tamaños de aerosoles considerado, factores como la carga electrostática del material del barbijo, o si el mismo está fabricado con textiles tejidos o no tejidos, influyen de manera significativa la eficiencia de filtrado (Drewnick et. al., 2020). La tabla 3 muestra la eficiencia de filtrado de diferentes barbijos usados en el modelado y descritos en la herramienta en línea de Jiménez. Barbijos genéricos se refiere a todos los barbijos sin certificación en su fabricación.

2.6. Tasa de emisión de CO₂

Durante la respiración humana no solamente se emiten aerosoles sino también gases como el dióxido de carbono (CO2). Si hay personas en un ambiente cerrado la concentración de CO₂ irá aumentando en función tanto a la actividad que realicen estas personas como a otros factores tales como sexo, edad, peso, etc. (Law et al. 2010) En la tabla 4 se resumen las tasas de emisión de CO₂ usadas en el presente estudio.

TABLA 3

Eficiencia de filtrado, en porcentaje, de diferentes tipos de barbijos tanto al exhalar como al inhalar (tomado de la herramienta en línea puesta por Jiménez)

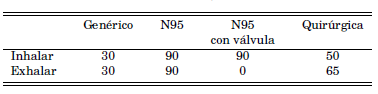
TABLA 4

Tasas de emisión de co₂ promedio para hombres y mujeres entre 2 1 y 30 años en función de la actividad (persily & de jonge 2017).

2.7. Ventilación y tasa de intercambio de aire

La ventilación se refiere al intercambio de aire del interior de un recinto con el aire del ambiente del exterior a través de los sistemas de ventilación tanto naturales como mecánicos. La tasa de intercambio de aire (ACH por sus siglas en inglés) es la tasa de ventilación del aire divido el volumen del espacio cerrado. Explícitamente, una ventilación o un ACH se refiere a que el 100% del aire del interior fue reemplazado por aire del exterior en una hora (REHVA, 2012).

 

3. INSTRUMENTOS Y MEDIDAS

En este estudio se usa la variación temporal de la concentración de CO₂ para estimar la ventilación en algunos ambientes cerrados y así calcular el ACH. En estos ambientes, la concentración de CO₂ se incrementa con el número de personas presentes en el mismo, ya que este gas es producto de la respiración, y se reduce debido a la ventilación natural o artificial del ambiente siguiendo una función exponencial la cual se aplica para el cálculo del ACH. Para los diferentes casos modelados y la estimación del ACH respectivo, se utilizaron dos analizadores portátiles de CO₂ (Air Visual Pro y Air Mentor Pro). Estos analizadores miden, además de CO₂, la concentración de material particulado suspendido en el aire, temperatura y humedad relativa del ambiente. En el caso del Air Visual los datos son guardados en su memoria interna cada 10 segundos y promediados posteriormente cada minuto mientras que el Air Mentor Pro despliega la concentración cada minuto y un promedio temporal cada 15 minutos.

 

4. PARAMETRIZACIÓN DEL MODELO Y DESCRIPCIÓN DE LOS CASOS DE ESTUDIO

El balance de masa para un ambiente en el que los aerosoles se distribuyen homogéneamente (Gam-maitoni & Nucci 1997) relaciona la concentración quanta (C, quanta m~³) con la tasa de emisión quanta (Eq, quanta hora^¹) y la tasa total de pérdida de quanta (A, hora^¹) mediante la ecuación 1:

donde V es el volumen del ambiente cerrado (m³), y A es la tasa total de pérdida de los quanta por ventilación, deposición y decaimiento de infectividad. La solución de la ecuación 1 viene dada por la ecuación 2. En ella se supone que C a tiempo cero es también cero.

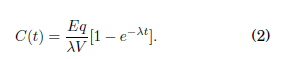
La probabilidad de contagio P (en %) en función implícita al tiempo (í) de exposición y la cantidad de quanta inhalada por la persona susceptible n, viene dada por la ecuación de Wells-Riley

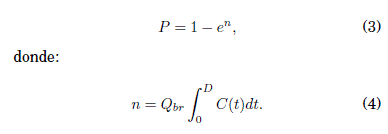
Aquí Qbr es la tasa de inhalación de la persona expuesta, y D es el tiempo total de exposición.

Tanto el cálculo de la concentración de quanta como la probabilidad de contagio son obtenidos suponiendo que (a) la tasa de emisión de quanta es constante y (b) el aire en el interior está bien mezclado por lo que no se toma en cuenta la posición espacial en la que la persona infectada se encuentra en el ambiente (Miller et al. 2020).

En base a las ecuaciones (3) y (4) se calculó la probabilidad de contagio para diferentes escenarios de exposición tales como (a) un aula de clases de la Universidad Mayor de San Andrés (UMSA), (b) un teatro de la ciudad de La Paz y (c) varios casos de trasporte público. Tanto la tasa de inhalación y los quanta emitidos fueron adecuados para cada escenario de acuerdo a nivel de actividad supuesto de las personas infectadas y susceptibles (tablas 1,2 y 4). En todos los escenarios se supuso que todas las personas usan barbijos genéricos (tabla 3) basados en una inspección visual del comportamiento de la población. En la tabla 5 se muestran parámetros usados para los diferentes escenarios.

4.1. Aula de clases

El aula de clases de la UMSA estudiada es relativamente grande en la cual normalmente pueden asistir a clases hasta 60 estudiantes (figura 4a). Sin embargo, para modelar la probabilidad de contagio se supuso que el aula se usa solamente al 50% de su capacidad, es decir con 30 estudiantes y un profesor el cual se supone es asintomático. Tanto el profesor como los estudiantes usan barbijos genéricos y los estudiantes siguen el protocolo de bioseguri-dad. Debido a que el aula es grande, el profesor tiene que hablar fuerte y caminar de un extremo a otro de la pizarra por lo que se puede considerar que realiza ejercicio ligero y a la vez habla fuerte por lo que se estima que emite 170 quanta horar¹ a largo de la clase que generalmente dura 120 minutos. Si asumimos que los estudiantes (personas susceptibles) están sentados tomando notas y sin hablar la tasa de inhalación estimada es de 0.52 m³ horar¹ por persona.

4.2. Teatro

El 17 de diciembre del 2020 se realizaron medidas en condiciones reales para medir la ventilación de un teatro en la ciudad de La Paz (figura 4b) con el objetivo de calcular la probabilidad de contagio de los asistentes. Ese día se tenía la presentación de un grupo de baile de 25 personas. El teatro tiene capacidad para 310 personas pero por las restricciones del momento sólo ingresaron 155 (50%).

Debido a la naturaleza del evento, durante la presentación, los integrantes del grupo de baile no usaron barbijos y la actividad física fue intensa por lo que los quanta emitidos se estimaron en 408 horar¹ por persona. El público en general estaba sentado sin mayor actividad y vistiendo barbijos genéricos por lo que la tasa de inhalación considerada fue de 0.52 m³ horar¹ y la emisión de CO₂ de 0.0056 litros s^¹.

Para diciembre del 2020, la tasa de incidencia de COVID-19 en La Paz fue de 1225 por cada 100000 habitantes (Cornejo 2020), lo que sugiere que 3 personas del total presente en el interior del teatro pudieron estar contagiadas. Para estudiar el efecto de asistir a eventos con estas características, asumimos que las 3 personas contagiadas pertenecían al grupo de baile.

4.3. Vehículos de transporte público: minibuses

En Latinoamérica el 68% de los viajes se realizan en transporte público (Pardo et al. 2021). Esto es particularmente importante al considerarse la probabilidad de contagio de los pasajeros y, aún más, de los conductores. Por esta razón se consideraron diferentes casos para estimar la probabilidad de infección por COVID-19 en viajes de minibús (vagonetas de tamaño mediano) con duración de una hora. Se tomó como referencia un minibús Toyota Hiace con 12 pasajeros (vehículo lleno). No se incluyen al chofer ni al pasajero a su lado ya que, actualmente (febrero 2021), en la mayoría de los minibuses, los asientos del conductor y acompañante están separados de los demás por una lámina de plástico. Las medidas típicas del largo, ancho y alto del interior son: 3 m de largo, 1.6 m de ancho x 1.3 m de alto dando un volumen de 6.2 m³. Se realizaron viajes en rutas del centro y zona sur de la ciudad de La Paz para verificar el tiempo de duración.

TABLA 5

Parámetros de los escenarios de exposición para los cuales se calculó la probabilidad de contagio.

 

5. RESULTADOS

5.1. Aula de clases

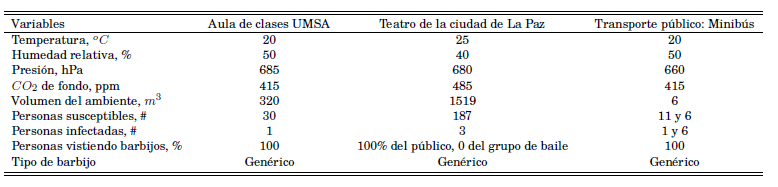
La fig. la muestra la variación de la concentración quanta promedio en función del tiempo de duración de la clase (evento) para diferentes tasas de ventilación. Claramente se observa que a medida que la clase se prolonga, la concentración de quanta va incrementando de manera no lineal siendo más peligroso para el caso en el que la ventilación sea baja (fig. la curvas en rojo) situación que puede darse si sólo se toma en cuenta la ventilación natural, es decir cerrando las ventanas y puertas. Por el contrario, si el aula contara (además de la ventilación natural) con ventilación forzada generada por ventanas abiertas o ventilación mecánica, el incremento de la concentración de quanta sería mucho menor (fig. la curvas en azul) aunque la clase se prolongue hasta los 120 minutos. De la misma manera, la probabilidad de contagio presenta una dependencia importante con la tasa de ventilación y el tiempo de duración de la clase. En la figura Ib se presenta la probabilidad de contagio en función a ambas variables. El caso más peligroso se da para bajas tasas de ventilación llegando a probabilidades de contagio del orden del 10% al final de la clase. Como se esperaba, la menor probabilidad de contagio de las personas susceptibles se da para situaciones en las que la clase dure poco tiempo y se tenga buena ventilación.

5.2. Teatro

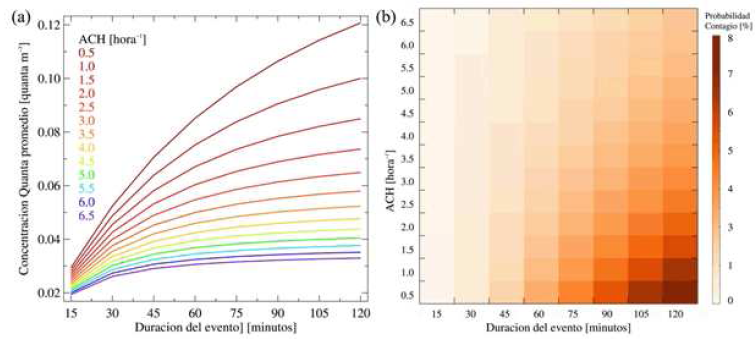
En la fig. 2 se muestran las medidas de CO₂ antes, durante y después del evento. Las medidas comenzaron en el teatro alrededor de las 4 pm con el grupo de baile ensayando para el evento hasta las 5 pm. En ese periodo se aprecia como la concentración de CO₂ sube sistemáticamente. A las 5:30 pm el público ingresa al teatro y el evento comenzó a las 6:00 pm momento en el que se cerraron todas las puertas. El CO₂ rápidamente sube su concentración hasta llegar a un máximo, 60 minutos después de iniciado el evento, de alrededor de 1900 ppm (fig. 2a) momento en el cual se abren las puertas para un receso. El evento termina a las 8:00 pm cuando el público sale del teatro y el mismo se cierra a las 9:00 pm. Los valores de CO2 al momento de cerrar el teatro están alrededor de 720 ppm y posteriormente comienzan a disminuir. En base a la disminución de la concentración de CO₂ se calcula que el teatro tiene una ventilación natural de 0.7 h'¹. Simulando la concentración de CO₂ en el interior del teatro se observa que a una tasa de ventilación de 0.7 hr¹ a los 60 minutos de iniciado el evento la concentración del CO₂ llega a valores aproximados a 1800 ppm (fig. 2b) lo cual está de acuerdo a las medidas realizadas. Esto muestra que el modelo funciona razonablemente bien ante situaciones reales. Finalmente, tomando en cuenta la tasa de ventilación calculada, la probabilidad que una persona se haya contagiado durante las dos horas que duró el evento es del orden del 25% (fig. 3).

5.3. Transporte público: minibuses

La probabilidad de infección por SARS-CoV-2 en viajes realizados en minibús fue estimada para los cuatro casos presentados en la Tabla 6. Se consideraron 12 pasajeros en todos los casos pero solo una persona infectada (11 susceptibles) en los dos primeros casos, mientras que se supuso que 6 pasajeros estaban infectados (6 susceptibles) en los dos últimos casos. En el Caso 1 se obtuvo una probabilidad de contagio del orden del 45% con las ventanas cerradas y una tasa de ventilación de 0.5 hora'¹. En el caso 2, basados en Ott et al. (2008), se incrementó la tasa de ventilación a 6.5 hora'¹ (ventanas parcialmente abiertas) mientras que se mantuvieron los demás parámetros iguales. La probabilidad de infección se redujo a aproximadamente 19%.

En el Caso 3, las ventanas se mantienen cerradas (ventilación de 0.5/t^¹) y en el Caso 4, las ventanas están abiertas por lo que la ventilación se considera de 20h~¹. La probabilidad de infección en el caso 3 es 97% y en el caso 4 se reduce a 39%. Menos de la mitad que en el Caso 3.

Como se indicó anteriormente, un parámetro útil para verificar una buena ventilación en ambientes cerrados es la concentración de CO₂ (Peng & Jiménez 2020). La OMS recomienda mantener la concentración de CO₂ a niveles menores a 800 ppm. Se ha medido de forma simple esta concentración para el caso de un minibús con 6 personas y 2 ventanas abiertas. La concentración promedio medida fue de 650 ppm aproximadamente en un trayecto de 10 minutos. Esto sugiere que mantener abiertas las ventanas, aunque sea parcialmente, reduce en gran medida las probabilidades de contagio del virus, por lo que realizar una caracterización más detallada de la ventilación en automóviles es fundamental para una mejor estimación de la probabilidad de contagio.

FlG. 1.— Tasa de ventilación y tiempo de duración del evento como factores relevantes en (a) concentración de quanta y (b) probabilidad de contagio para el escenario de un aula de la UMSA.

FlG. 2.— (a) Medidas de CO2 en un teatro de la ciudad de La Paz antes, durante y después de una presentación de baile. Las líneas verticales indican (de derecha a izquierda) inicio del ensayo del grupo, inicio del evento, fin del evento y cierre del teatro, (b) Simulación de las concentraciones de CO2 para diferentes tasas de ventilación en función del tiempo.

TABLA 6

Probabilidad de Infección por Covid-19 en para diferentes condiciones en minibuses en la ciudad de La Paz.

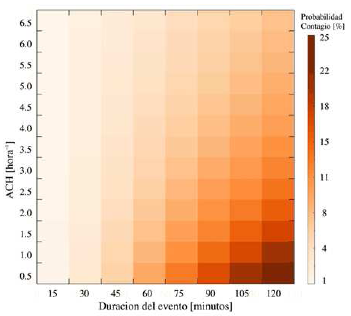
FlG. 3.— Probabilidad de contagio en función de la duración de los eventos y de la ventilación de los ambientes para un teatro en la ciudad de La Paz.

 

6. DISCUSIÓN

Los resultados del modelado para los ambientes cerrados estudiados muestran claramente que la probabilidad de contagio sube con el tiempo de permanencia en el recinto así como con baja ventilación. Por ejemplo, para el caso de un aula en la UMSA, para una clase de 2 h de duración con la mitad de la capacidad del aula llena, con todos los participantes usando barbijos y con una sola persona contagiada (el instructor) hablando fuerte frente al pizarrón el orden de magnitud de la probabilidad de contagio es del 10% (fig. 1). Si bien hay varios supuestos para arribar a este número, por ejemplo, la persona contagiada podría ser un estudiante en vez del instructor, o los estudiantes podrían hablar entre ellos en ciertos intervalos, etc., cambios razonables en los supuestos empleados muestran que la probabilidad de contagio se mantiene en ese orden de magnitud.

Para el caso del teatro, donde un mayor número de parámetros fueron medidos experimentalmente, la probabilidad de contagio es del orden del 25% (fig. 3) para un evento que dura 2 h (como el caso estudiado). Para este lugar en particular, la ventilación natural (medida) es 0.7 h~¹, que está por debajo de los 6 intercambios por hora sugerido por la OMS (Atkinson & World-Health-Organization 2009). En este caso también se observa que incrementando la ventilación a 6 h^¹ la probabilidad de contagio podría reducirse a un 8%. Finalmente, las medidas de la concentración máximas de CO₂, del orden de 1900 ppm, son comparables a las estimadas con los supuestos usados en el modelo. Esto da confianza a los resultados obtenidos.

Por otro lado, dado que en general el transporte por minibuses es lento debido al intenso tráfico vehicular, los tiempos de transporte son, en promedio, mayores a 30 minutos y hasta mayores a una hora (Pacoricona-Laguna 2014) (por ejemplo, para el caso de un viaje entre las ciudades de El Alto y La Paz). En ese sentido los resultados para el transporte sugieren que una adecuada tasa de ventilación tiene una gran importancia para reducir la probabilidad de contagio de la COVID-19 en el transporte por minibús, que es el transporte masivo en Bolivia. Basados en estudios previos es posible que en muchos minibuses esta ventilación pueda lograrse abriendo las ventanas al menos unos 10 cm (Ott et al. 2008), sin embargo, es necesario realizar más estudios donde se mida experimentalmente la ventilación y así se reduzca la incertidumbre y mejoren los resultados del modelo.

Por la naturaleza del procedimiento empleado existen varias incertidumbres asociadas a los resultados del modelado: los supuestos y los parámetros empleados principalmente. A pesar de esto, el modelo permite estimar el orden de magnitud relativo de las probabilidades de contagio lo cual puede ser usado como una guía para tomar decisiones de protección y cuidado de las personas. Por ejemplo los resultados sugieren que es mejor tener eventos cortos a eventos largos; que la ventilación del ambiente es de fundamental importancia o que el uso de barbijos es importante.

Para minimizar la transmisión de COVID-19 entre los pasajeros del transporte público en Latinoamérica (Pardo et al. 2021) recomiendan medidas tales como: ventilación adecuada (4-6 intercambios por hora), distancia/duración del viaje (menor a 15 minutos), medidas de protección (uso de barbijos y otras medidas de protección) y comportamiento de los pasajeros (silencio). El modelo que utilizamos incorpora estos parámetros y se puede evidenciar en los resultados obtenidos ya que la probabilidad de contagio se reduce cuando se cumplen estas medidas. Como siguiente paso se planea realizar mediciones de la ventilación (ACH) en el transporte público del área metropolitana de La Paz y El Alto para establecer cuál sería la probabilidad de contagio de los pasajeros reduciendo las incertidumbres al realizar medidas en campo en vez de usar supuestos o referencias encontradas en la literatura.

 

7. CONCLUSIONES

A la fecha existe suficiente evidencia científica que señala que la forma más importante de transmisión del virus SARS-CoV-2 se da a través de aerosoles respiratorios en ambientes cerrados. Por ello en este trabajo se analizaron tres casos a través de la aplicación de un modelo matemático que representa varios de los procesos más importantes.

Como resultado del modelado aplicado a las tres situaciones escogidas en este estudio podemos concluir lo siguiente:

FlG. 4.— Ambientes cerrados para los cuales se calculó la probabilidad de contagio (a) aula de la UMSA y (b) un teatro en la ciudad de La Paz.

•  La ventilación es la manera más simple (y probablemente más barata a la larga) de reducir las probabilidades de contagio entre las personas.

•  En ambientes cerrados como aulas de enseñanza y teatros, acciones como abrir puertas y ventanas, contribuyen positivamente a mantener una buena calidad del aire pero puede que ventilación mecánica sea necesaria para reducir aún más las probabilidades del contagio.

•  El uso de barbijos, bien ajustados a la cara, y el lavado de manos con agua y jabón siguen siendo esenciales para evitar contagios.

•  Mantener las ventanas abiertas en el transporte público reduce la probabilidad de contagio por COVID-19 al incrementar el intercambio de aire limpio con el exterior.

•  Los buses de transporte interdepartamental, en muchos de los cuales no se puede abrir ventanas, deben permitir intercambio de aire con el exterior a través de su sistema central de climatización. Será importante medir la calidad del aire en condiciones reales para establecer de manera experimental si los niveles de ventilación son adecuados.

•  En ambientes cerrados no es buena práctica usar ventiladores de techo o calentadores con ventilador pues los mismos no ayudan al intercambio de aire con el exterior y solo dispersan más rápido los aerosoles en el mencionado ambiente.

Conflicto de intereses

Los autores declaran que no hay conflicto de intereses con respecto a la publicación de éste documento.

 

Notas

¹    https://www.who.int/news-room/commentaries/detail/modes-of-transmission-of-virus-causing-covid-19-implications-for-ipc-precaution-recommendations

²  https://www.who.int/news-rooin/commentaries/detail/transmission-of-sars-cov-2-implications-for-infection-prevention-precautions

³ https://tinyurl.coin/covid-estimator

 

REFERENCIAS

Adams, W. C. 1993, Measurement of Breatliing Rate and Vol-ume in Routinely performed Daily Activities (California Envi-ronmental Protection Agency, Air Resources Board)        [ Links ]

Atkinson, J. & World-Health-Organization. 2009, Natural Venti-lation for Infection Control in Health-Care Settings (Geneva: World Health Organization)        [ Links ]

Buonanno, G., Stabile, L., & Morawska, L. 2020, Environment International, 141, 105794        [ Links ]

Cornejo, P. A. 2020, Boletín Epidemiológico "Noticias COVID-19" (Colegio de Biólogos La Paz)        [ Links ]

Dabisch, P. et al. 2020, Aerosol Science and Technology, 55, 142        [ Links ]

Gammaitoni, L. & Nucci, M. C. 1997, Emerging Infectious Dis-eases, 3 (3), 335

Harvey, A. P. et al. 2021, Environ. Sci. Technol. Lett., 8 (2), 168        [ Links ]

Johnson, G. R. et al. 2011, Journal of Aerosol Science, 42 (12), 839

Knibbs, L. D. et al. 2011, American Journal of Infection Control, 39(10), 866

Law, J., Watkins, S., & Alexander, D. 2010, American Journal of Infection Control, 216126, 2010

Madueño, L., Kecorius, S., Andrade, M., & Wiedensohler, A. 2020, Atmosphere, 11 (6), 598

Madueño, L. et al. 2019, Environmental Pollution, 248, 295

Mikhailov, E., Vlasenko, S., Niessner, R., & Póschl, U. 2004, At-mos. Chem. Phys., 4, 323        [ Links ]

Miller, S. L. et al. 2020, Indoor Air, 31, 314

Morawska, L. & Milton, D. K. 2020, Clinical Infectious Diseases, 71(9), 2311

Morawska, L. et al. 2009, Journal of Aerosol Science, 40 (3), 256

Ott, W., Klepeis, N., & Switzer., P. 2008, Journal of Exposure Science & Environmental Epidemiology, 18 (3), 312        [ Links ]

Pacoricona-Laguna, V. 2014, Estructura y funcionamiento del sistema de transporte público urbano en el municipio de La Paz (Tesis de Licenciatura. Facultad de Ciencias Financieras y Económicas, UMSA)        [ Links ]

Pardo, C. F. et al. 2021, Infectio, 25 (3), 182

Peng, Z. & Jiménez, J. L. 2020, doi:10.1021/acs.estlett.lc00183

Persily, A. & de Jonge, L. 2017, Indoor Air, 27 (5), 868

Riley, E. C, Murphy, G., & Riley, R. L. 1978, American Journal of Epidemiology, 107 (5), 421

Yang, W. & Marr, L. C. 2011, Dynamics of Airborne Influenza A Viruses Indoors and Dependence on Humidity. PLoS ONE, 6 (6), e21481        [ Links ]

Zhang, R. et al. 2020, Proceedings of the National Academy of Sciences, 117 (26), 14857