A. ARTÍCULOS

 

Modelo de autómata celular para la propagación de Covid-19

A cellular automaton model for the spread of Covid 19

 

 

Alejandra Vargas^†, Flavio Ghezzi, Armando R. Ticona-Bustillos
^†avargas@fcpn.edu.bo
Instituto de Investigaciones Físicas, Universidad Mayor de San Andrés
Campus Universitario, c. 27 Cota-Cota, Casilla de Correos 8635
La Paz - Bolivia
(Recibido 26 de noviembre de 2020; aceptado 10 de diciembre de 2020)

 

 

---

Resumen

En este trabajo se emplea el método de autómatas celular para simular la propagación del Covid-19, en sistemas pequeños, considerando cinco grupos de interés: individuos sanos, expuestos, infectados, recuperados y también los vacunados; no se toman en cuenta los individuos asintomáticos y los decesos, por representar un porcentaje bajo. Uno de los parámetros más relevantes en el sistema es la movilidad, esto hace referencia a la cantidad de individuos que se desplazan en el sistema al mismo tiempo. Variando los niveles de movilidad en un sistema, comprobamos que mientras menor sea esta, el pico máximo de contagio, es alcanzado de manera más lenta y con un valor menor de contagios, en comparación al caso en el que toda la población se mueve al mismo tiempo, lo cual es bastante importante para no tener un sistema de salud colapsado. El sistema en el que se tiene individuos vacunados muestra mejores resultados que el caso de la restricción de movilidad. Por último, también se modela un sistema de tamaño único y constante, siendo la variable la población. Como era de esperar, esta parte del modelo demuestra la importancia del distanciamiento social, ya que en sistemas con muchos individuos en espacios pequeños y cerrados, el pico máximo de contagio se alcanza en tiempos más breves, que en sistemas con pocos individuos.

Descriptores: Técnicas computacionales - caminos aleatorios - enfermedades.

Código(s) PACS: 02.70.-c, 05.40.Fb, 87.19.xd

---

Abstract

In this paper we use the cellular automaton method to simulate the spread of Covid-19 in small systems. Five groups of interest are considered: healthy, exposed, infected, recovered and vaccinated individuals. Asymptomatic individuals and deaths are not taken into account as they represent a low percentage of the population. One of the most relevant parameters in the system is mobility, which refers to the number of individuals moving in the system at the same time. By varying the levels of mobility in the system, we saw that the lower the mobility, the slower it was to reach the peak of contagion and the lower the number of contagions compared to the case in which the entire population moves at the same time, which is quite important in order to avoid a collapsed health system. The system with vaccinated individuals showed better results than the mobility restriction case. Finally, a one-size-fits-all, constant-size system is also modelled in which results showed the variable being the population. As expected, this part of the model demonstrates the importance of social distancing, since in systems with many individuals in small enclosed spaces, the maximum peak of contagion is reached in shorter times than in systems with fewer individuals.

Subject headings: Computational techniques - random walks - diseases.

---

 

1  Introducción

Los últimos meses el mundo ha enfrentado a un enemigo común, el SARS-CoV-2 (Síndrome Respiratorio Agudo Severo Coronavirus 2), más conocido como Covid-19, mismo que tuvo origen en la ciudad de Wuhan en China e inició desde el mes de diciembre del 2019. En marzo del 2020 se declaró que al brote del Covid-19 como pandemia debido a que este se extendió en el mundo en pocos meses como lo señala la [122020Organización Mundial de la Salud]. Esta enfermedad infecciosa, se trasmite de persona a persona, a través de gotitas respiratorias producidas por la persona infectada. A partir de ello, los gobiernos de diferentes países han tenido que poner en práctica diferentes estrategias de mitigación para controlar la pandemia, generando distanciamiento social, restringiendo los viajes nacionales e internacionales, cuarentenas rígidas, aislamientos y confinamientos que podían reducir efectivamente la posibilidad de contacto humano como se cita en [82020Ghosh & Bhattacharya], [32020Bohórquez et al.Bohórquez, Deisy Marcela Muñoz Morales, Arrieta, Prieto, Alarcón, & Unidad Investigación Usta] y [92020Gutiérrez-Aguilar et al.Gutiérrez-Aguilar, Córdova-Lepe, Muñoz-Quezada, & Gutiérrez-Jara]. Estas medidas de restricción contribuyen a que la propagación del virus sea más paulatina; sin embargo, conlleva a algunos problemas psicológicos, sociales y económicos tal como lo menciona en su artículo [102020Locht]. Una solución más efectiva pero a largo plazo, es la vacuna contra el Covid-19. Actualmente, varios países se encuentran en diferentes fases de desarrollo de esta vacuna ([112020Medina et al.Medina, Jaramillo-Valverde, et al.])

Los modelos basados en agentes o autómatas celulares, adquirieron relevancia al intentar modelar el comportamiento de la propagación de epidemias en redes complejas, teniendo una capacidad de generar dinámicas que reproducen los procesos tradicionales, basados en la difusión, siendo capaces de reproducir fenómenos que son complejos desde el punto de vista de la dinámica determinista no lineal como se menciona en [22016Banisch].

Los modelos estocásticos basados en agentes o autómatas celulares son una alternativa a los modelos basados en ecuaciones diferenciales. Estos son modelos discretos de carácter individual, que describen sistemas espaciales dinámicos en los que el estado de cada celda depende de los estados previos de las celdas vecinas, de acuerdo con un conjunto de reglas de transición descrito en [72013Fresnadillo Martínez et al.Fresnadillo Martínez, García-Sánchez, García-Merino, del Rey, & García-Sánchez].

Se han realizado algunas adaptaciones de modelos basados en agentes, ajustados a condiciones de la actual epidemia producida por el Covid-19 en diferentes regiones como se muestra en [62020Echeverri et al.Echeverri, Cabrera, & Echeverri], [12006Aguilera] y [42016Cano & Rojas], esto para observar la evolución de esta enfermedad en sistemas cerrados o aislados, en los que interviene principalmente la movilidad de la población; como también para estimar los efectos de una cuarentena rígida, flexible o en el peor de los casos un sistema sin ninguna restricción.

En la presente investigación se adapta un modelo de crecimiento microbiano a la propagación de la epidemia en sistemas cerrados, empleando cinco grupos de interés: vacunados (V), sanos (S), incubando (I), enfermos (E) y recuperados (R). Esto permite caracterizar la evolución en el tiempo y el espacio en proporción a la cantidad de individuos en los distintos grupos de interés mencionados, teniendo en cuenta diferentes condiciones de movilidad del sistema. No obstante, este modelo no contempla los individuos asintomáticos, ni tampoco los decesos en el sistema, debido a que los porcentajes de estos individuos son pequeños, comparado con los otros grupos de interés hasta la actualidad como se señala en [52020Cruz et al.Cruz, Santos, Cervantes, & Juárez].

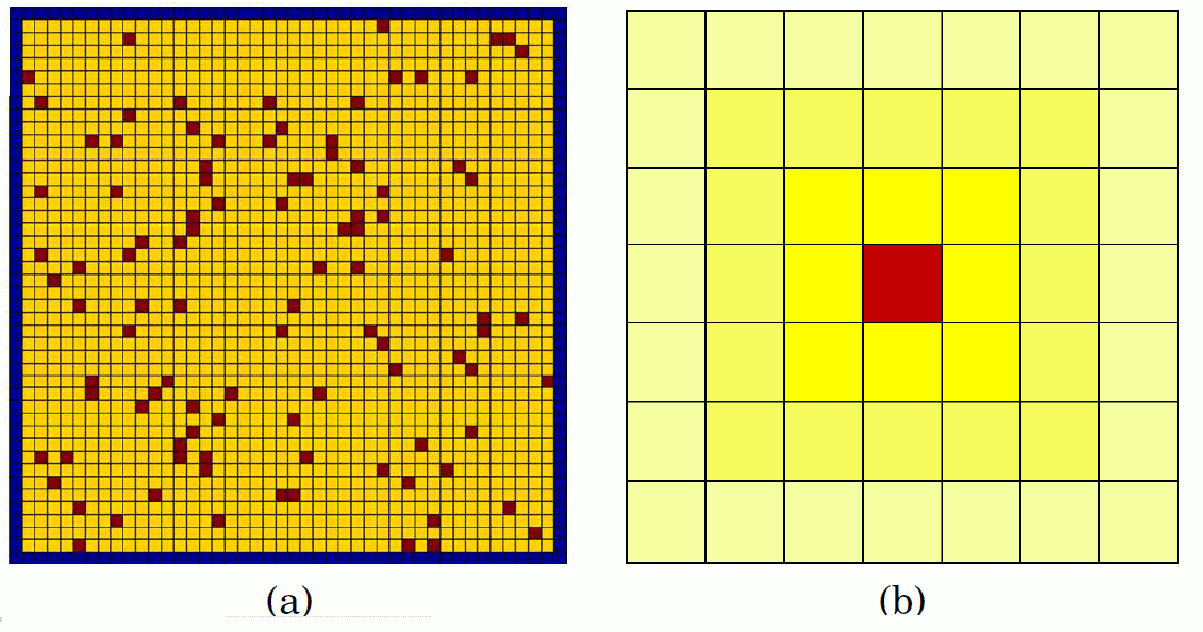
Figure 1: (a) Matriz cuadrática L×L, las celdas azules corresponden a las paredes, las celdas amarillas son espacios vacíos y las celdas rojas son individuos. (b) Un individuo en una posición (i,j) (en rojo) y sus 48 vecinos cercanos.

El artículo está estructurado de la siguiente manera: En la Sec. 2, se plantea un modelo describiendo la propagación de la epidemia, del cual se tienen tres variantes, una de las cuales tiene en cuenta la variación de movilidad en el sistema, la segunda considera además porcentajes de población vacunada y la siguiente considera un espacio de tamaño constante en el que se varía la cantidad de población dentro del sistema. La dinámica resultante para los modelos es expuesta en la Sec. 3. Las implicaciones de los resultados se discuten en la Sec. 4 y finalmente en la Sec. 5 se expresan las conclusiones y perspectivas de esta investigación.

 

2  MODELO

Para modelar el espacio – temporal de la epidemia se propone un modelo dinámico basado en autómatas celulares, debido a que estos modelos ayudan a representar resultados macroscópicamente complejos, al tiempo que se basa en interacciones locales que dependen de la interacción de una multitud de individuos como se manifiesta en [62020Echeverri et al.Echeverri, Cabrera, & Echeverri], [12006Aguilera] y [42016Cano & Rojas].

Siendo la base de esta investigación un modelo capaz de caracterizar las transiciones de fase de gas – líquido en redes bidimensionales, mediante el comportamiento de las colisiones en función al número de partículas y las características de los cúmulos formados por las mismas, modelo que fue validado, modificado y adaptado para determinar la propagación de la epidemia en sistemas cerrados.

2.1  Modelo en el que varía la movilidad del sistema

El modelo adaptado para la propagación de la epidemia, utiliza una autómata celular que consiste en una matriz cuadrada L×L, que tiene seis estados: -2, 0, 1, ′m′, ′n′ y > n como se observa en la Tabla 1.

Table 1: Estados de interés para las simulaciones

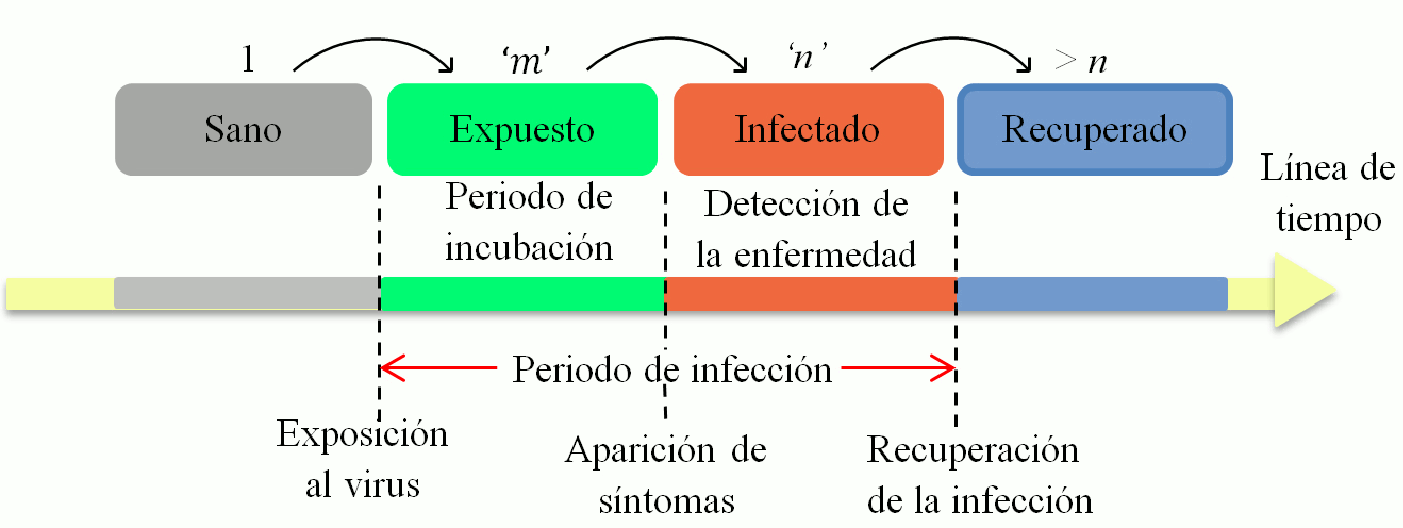
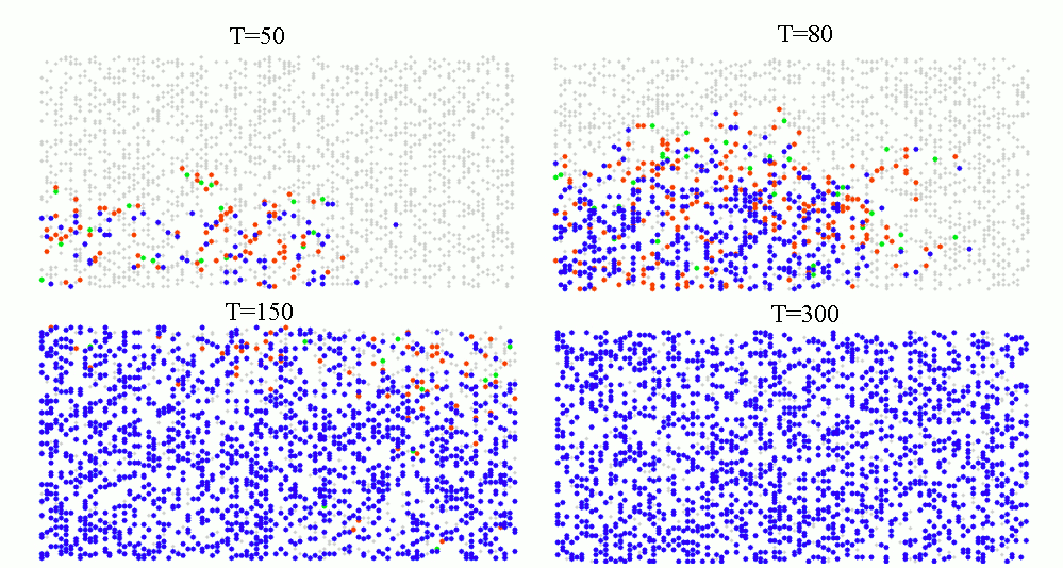
Figure 2: (a) Los individuos plomos representan la población (S), los verdes la población (I), los rojos la población (E) y los azules corresponden a la población (R). A) Esquema de la dinámica de transmisión de enfermedad. (b) Evolución temporal de la red superficial durante la propagación de la infección en la población.

La matriz estará definida inicialmente vacía A(i,j)=0, con sus respectivas paredes A(i,j)=−2. Posteriormente se sortean aleatoriamente las posiciones iniciales para cada individuo dentro de la matriz, teniendo las siguientes posibilidades: A(i,j)=1, A(i,j)=m, A(i,j)=n, A(i,j) ≥ n, tal como se observa en la Fig. 1(a).

El estado de un individuo en una etapa estará dado por A_(i,j)^(t), que dependerá del estado de los individuos vecinos en etapas anteriores. En el modelo se considera que para un tiempo “t”, un individuo puede tener una interacción con sus 8, 16 o 48 vecinos cercanos, es decir que puede moverse a su primera, segunda y tercera vecindad a cada paso de la simulación, donde las tres posibilidades son equiprobables como se observa en la Fig. 1(b) . El desplazamiento de una sola posición produce una dinámica muy lenta que no representa correctamente la movilidad de los individuos que queremos estudiar en el presente caso.

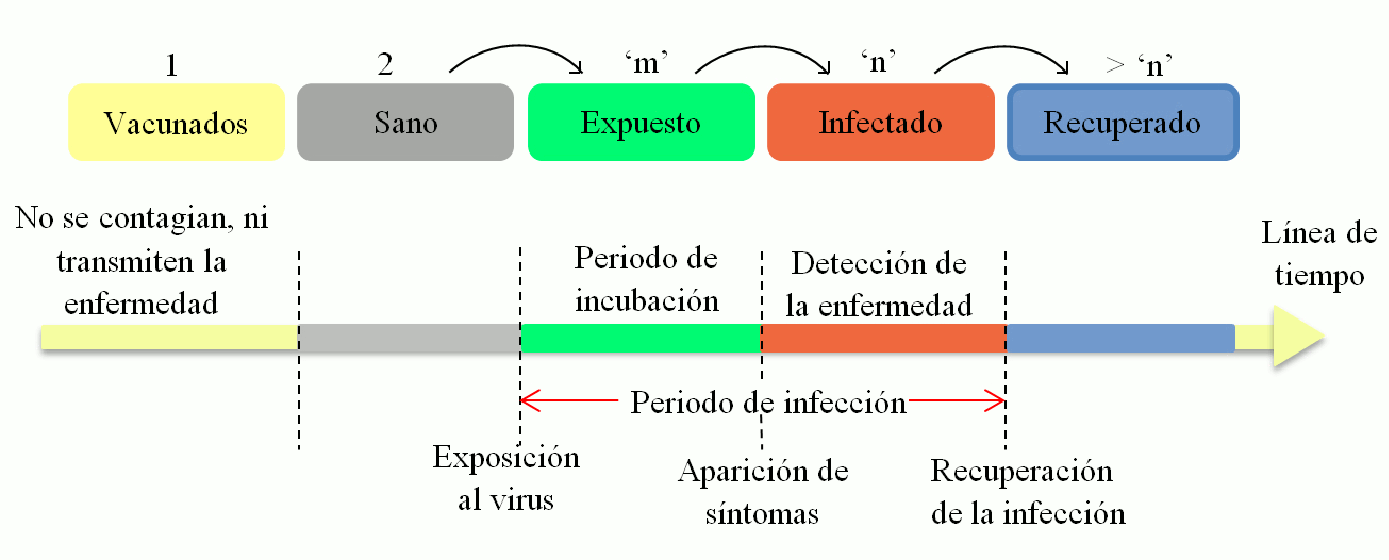
Figure 3: Esquema de la dinámica de transmisión de enfermedad. Los individuos amarillos corresponden a la población (V), los plomos representan la población (S), los verdes la población (I), los rojos la población (E) y los azules corresponden a la población (R).

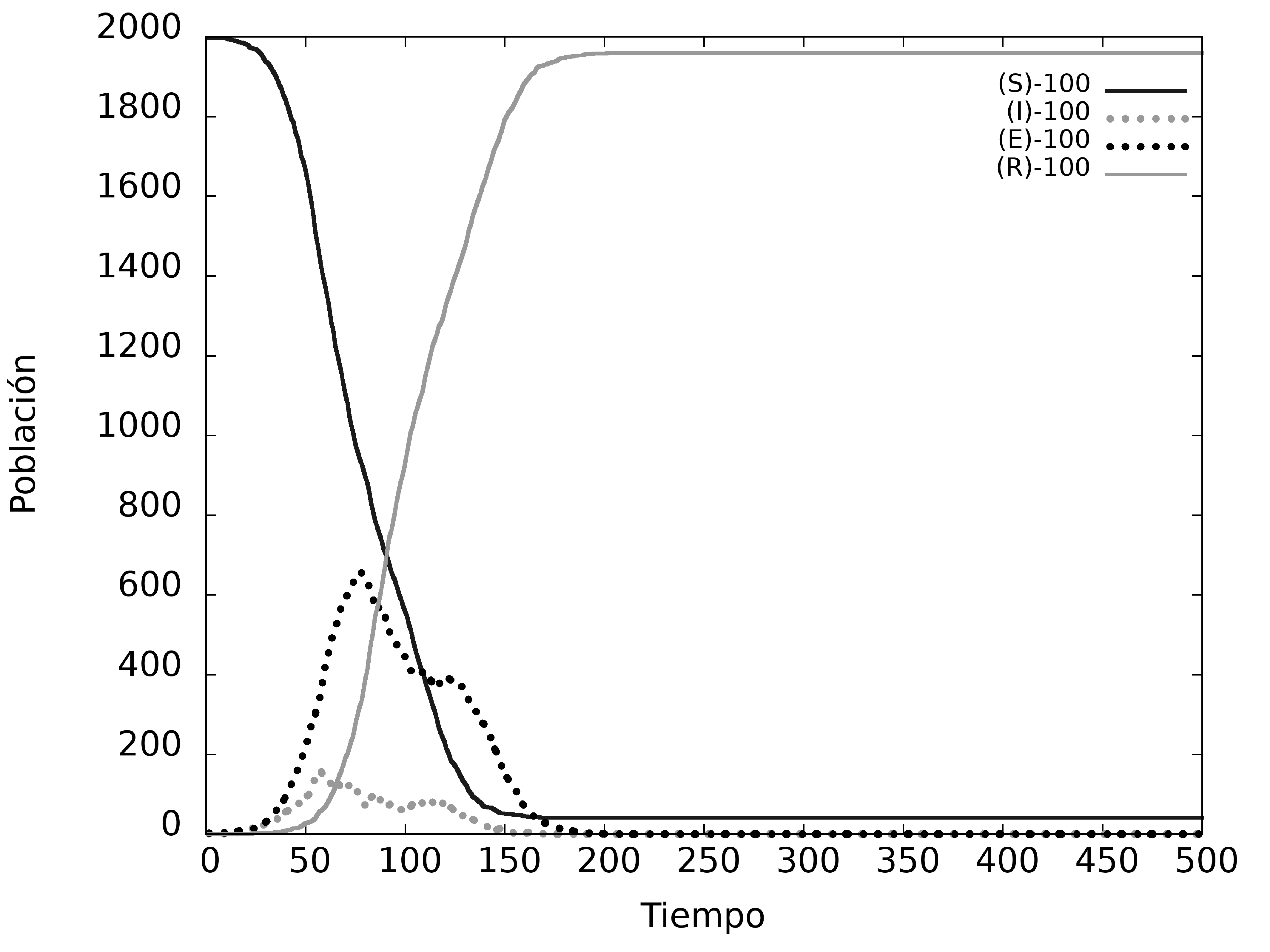
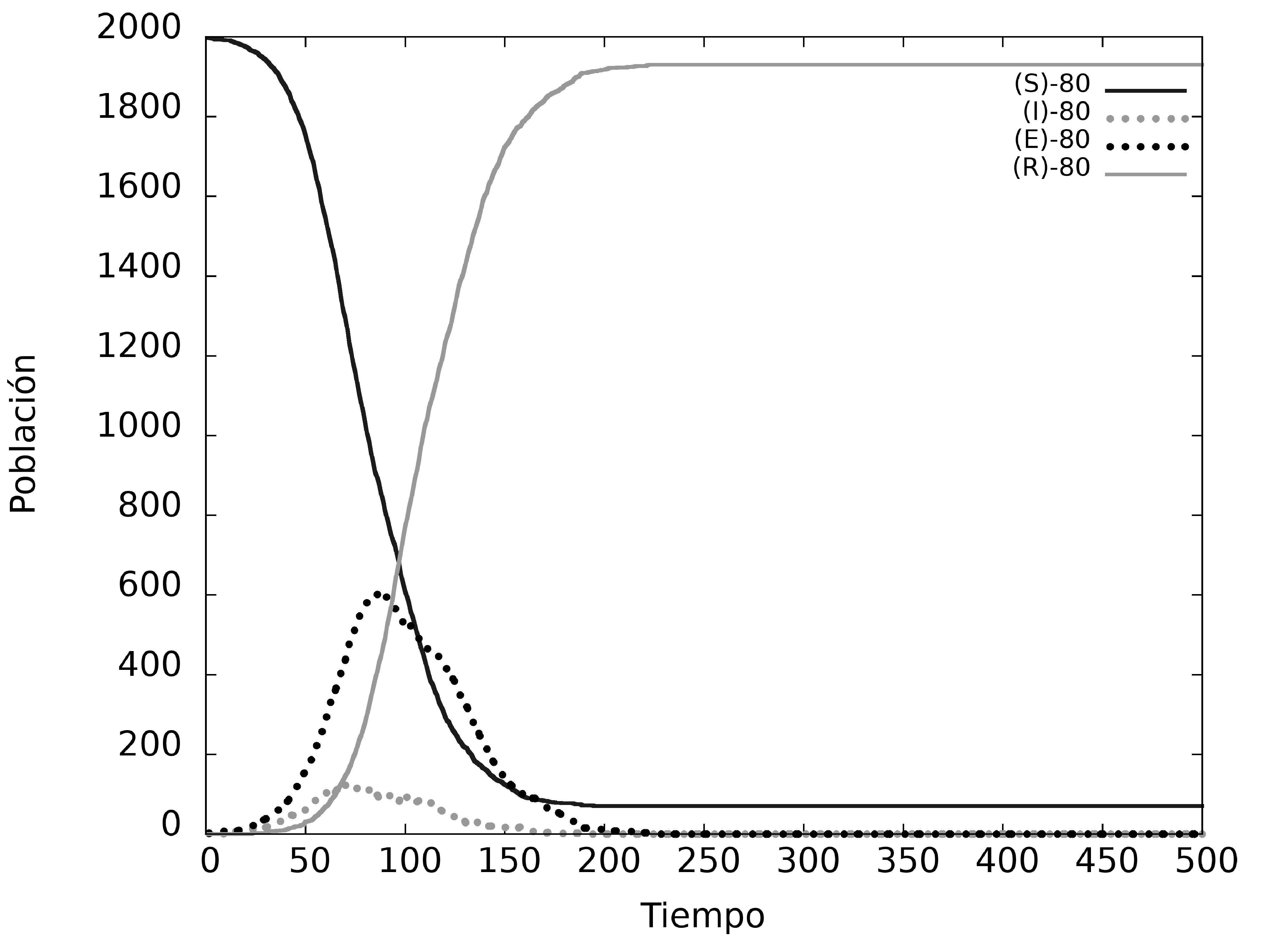
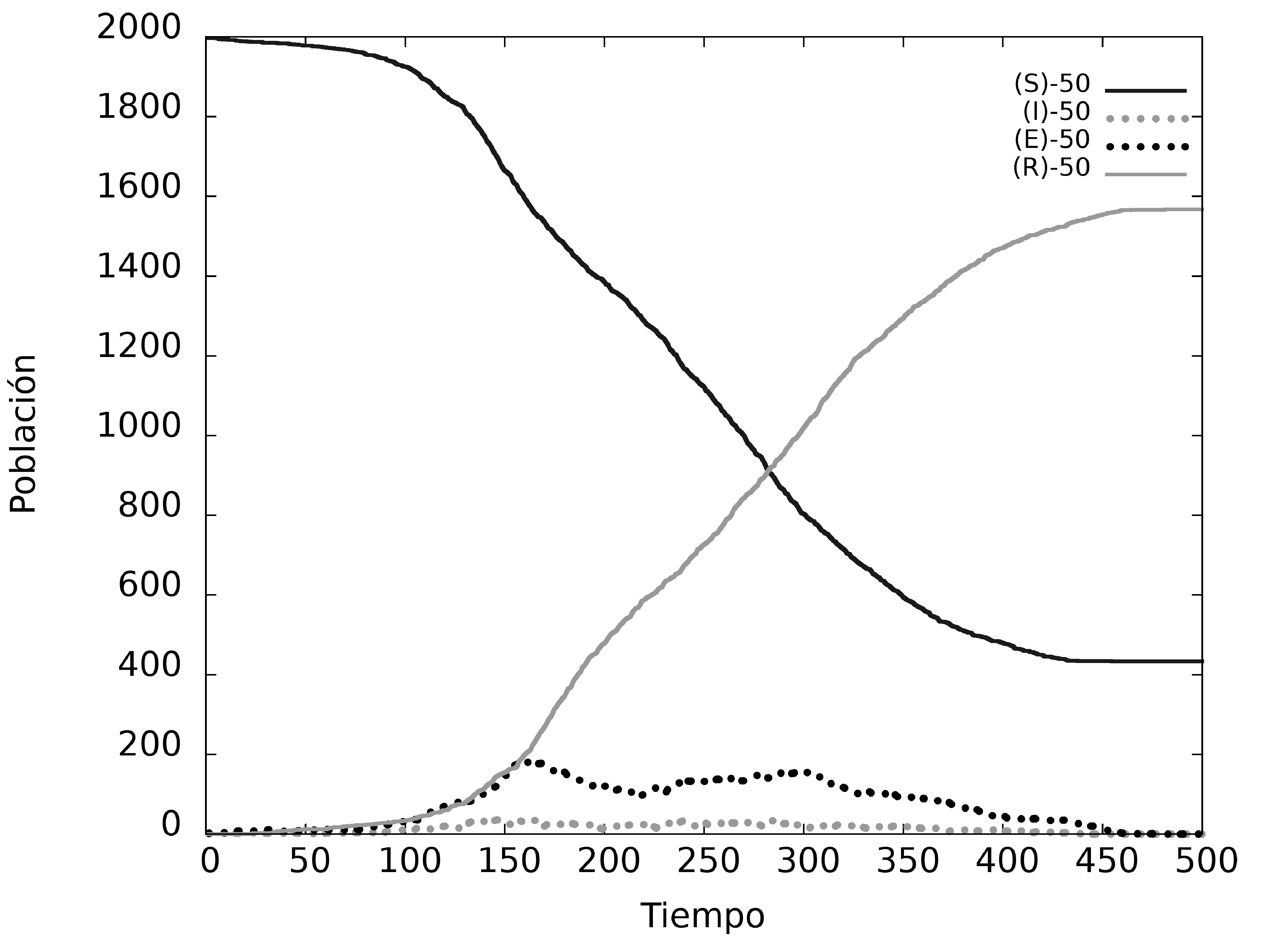
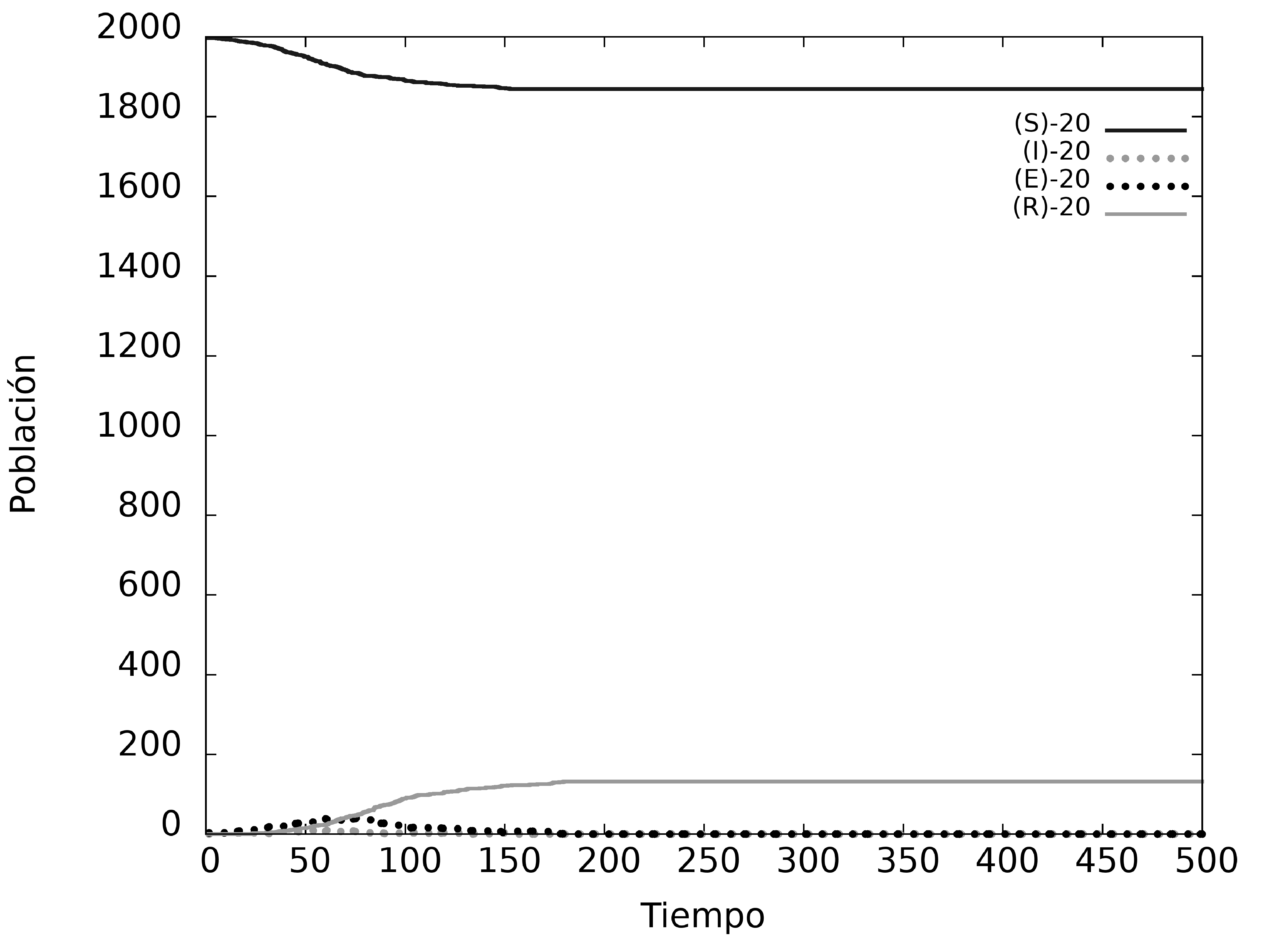
Figure 4: Dinámica del modelo con individuos N=2000, en una matriz de L=100, variando la movilidad de la población (100, 80, 50 y 20%).

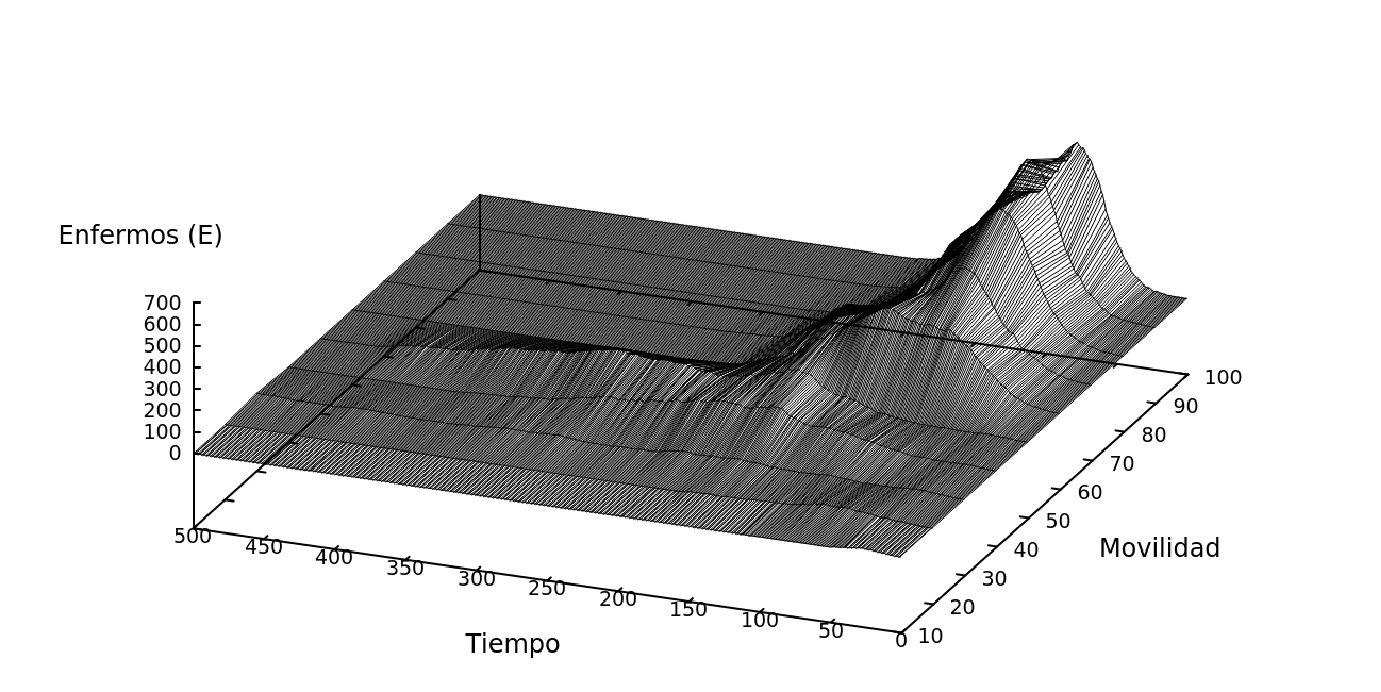
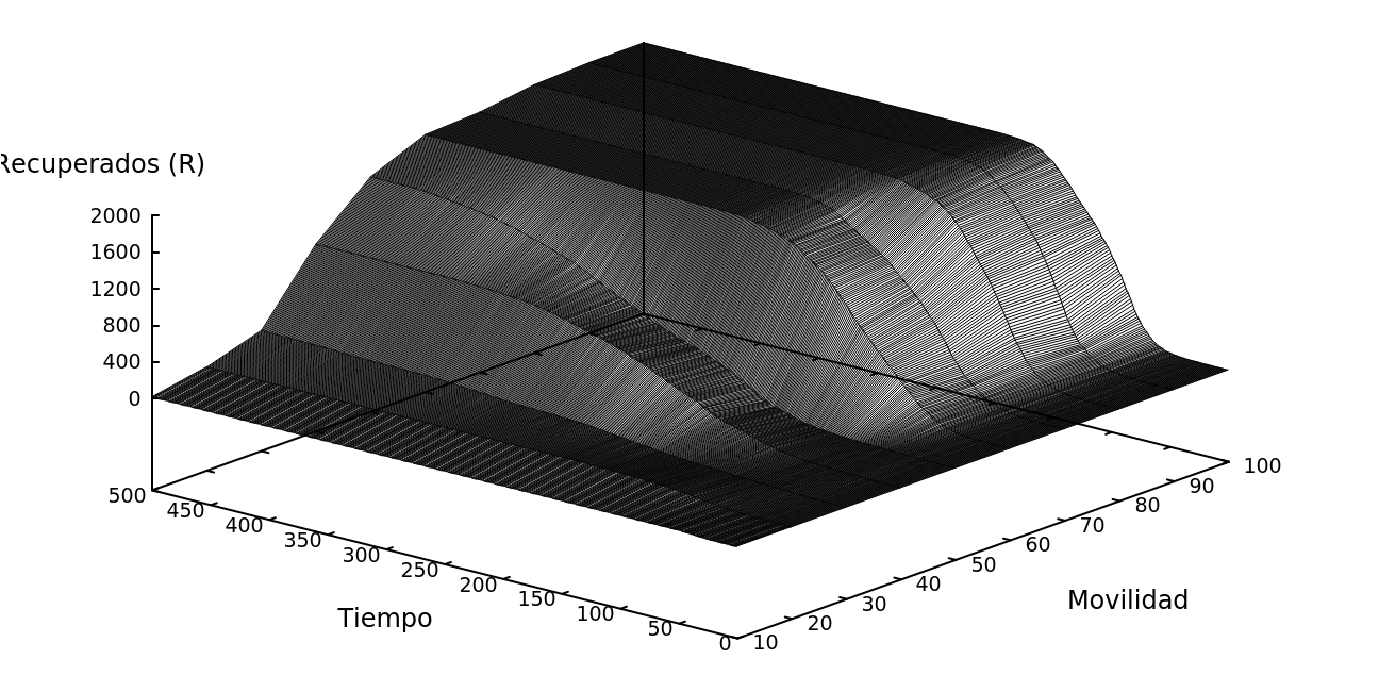
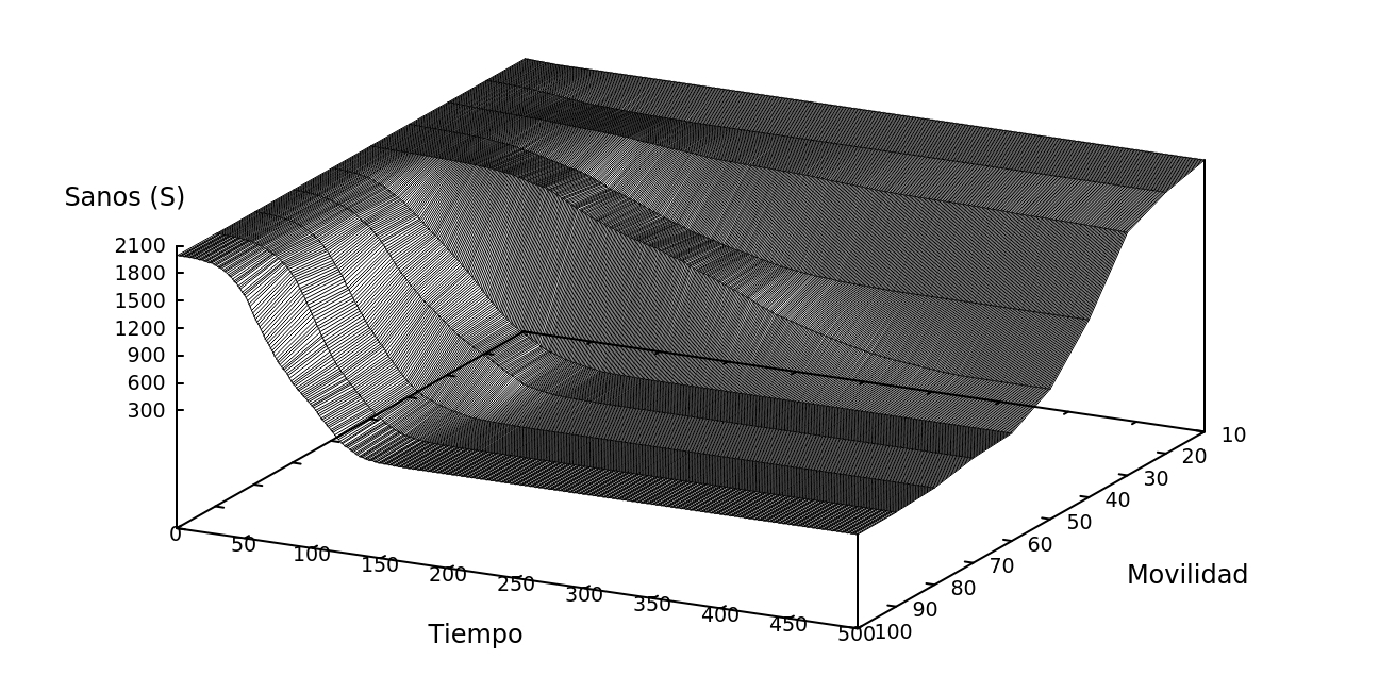
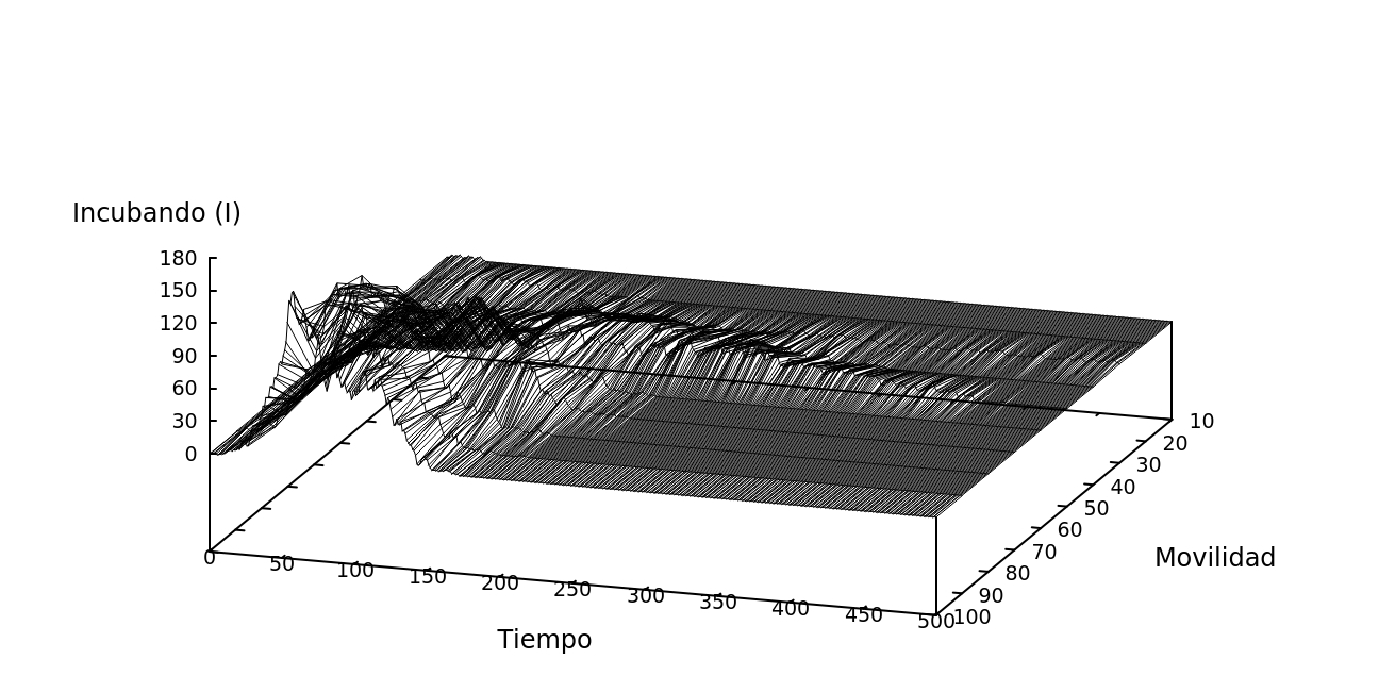
Figure 5: Los cuatro grupos de interes (sanos, incubando, enfermos y recuperados) , variando la movilidad de la población.

El modelo tiene 4 grupos de interés ((S), (I), (E) y (R)) para todos los individuos de la matriz; inicialmente todos los individuos están sanos, posteriormente en el tiempo “t=0” algunos individuos se exponen a la infección.

Todos los individuos se mueven bajo el efecto del caminante aleatorio y pueden desplazarse hasta la tercera vecindad para un solo tiempo. Si la posición sorteada para un individuo enfermo (E) corresponde a la posición de un individuo sano (S) recién este se infecta (no hay contagio por proximidad solo por interacción directa). Por otro lado si un individuo sano (S), tiene una interacción directa con uno enfermo (E) este también se contagia. Una vez que un individuo se contagie, existe un periodo de incubación denominado ′m′, tiempo en el cual el individuo es capaz de contagiar (′m′ es el periodo de incubación para el Covid-19, que corresponde a 5.2 días, tiempo en el cual el individuo está enfermo, pero no presenta síntomas como se expone en [132020Wang et al.Wang, Pan, Wan, Tan, Xu, Ho, & Ho]), Fig. 2.

El modelo contempla diferentes condiciones de movilidad del sistema. Es decir podemos variar en el sistema la cantidad de individuos que se mueven o se quedan en reposo. En el peor escenario se considera que el 100% de los individuos se mueve al mismo tiempo. Sin embargo, para poder observar la evolución temporal de la epidemia en regiones con cuarentena se redujo la movilidad del sistema hasta tener solo un 10% de población en movimiento.

2.2  Modelo en el que se consideran individuos vacunados

Este modelo añade el estado de ‘individuo vacunado’ dentro de la matriz L×L, teniendo siete posibles estados: -2, 0, 1, 2, 3, ′m′, ′n′ y > ′n′ (Tabla 1). Para realizar esta simulación, consideramos que la vacuna introducida en nuestro sistema es 100% efectiva y que una vez que un individuo es vacunado, este no puede contraer nuevamente la enfermedad tal como se oberva en la Fig. 3.

En este modelo variamos el porcentaje de individuos vacunados en el sistema para observar la relación que existe con el pico máximo de contagios.

2.3  Modelo en el que se tiene un espacio constante y se varía la cantidad de individuos

Este modelo emplea los mismos grupos de interés de la Tabla 1, la diferencia es que ahora en vez de variar la movilidad del sistema se cambia la cantidad de individuos, llenando cada vez más la matriz L×L.
La información obtenida de las tres variantes del modelo es presentada en la siguiente sección, dejando para la Sec. 4 la discusión de las mismas.

3  Resultados

3.1  Variación de la movilidad en el sistema

Para modelar el sistema utilizamos diferentes coeficientes de movilidad, fijamos el tamaño del sistema y la cantidad de individuos (usando un porcentaje de 20%). En el primer caso consideramos que el 100% de los individuos se mueve dentro de nuestra red bidimensional al mismo tiempo. En el segundo caso se mueve el 80% de la población, quedando el otro 20% en reposo. En la Fig. 4(c) se observa que se mueve solo la mitad de la población (50% ) y en la Fig. 4(d) únicamente se mueve el 20% de la población total.

Podemos observar que existen variaciones considerables entre los sistemas con mayor y menor movilidad en los cuato grupos de interes (sanos, incubando, enfermos y recuperados), por lo cual la Fig. 5 muestra esta variación desde 10% hasta 100%.
Las variaciones que generan los diferentes grados de movilidad en el sistema se comprueban al realizar la medida del desplazamiento cuádratico medio para cada caso, lo cual muestra que el sistema se encuentra funcionando de la manera adecuada.'

La evolución temporal para los cuatro sistemas en los cuales varía la movilidad se muestra en la Fig. 6.

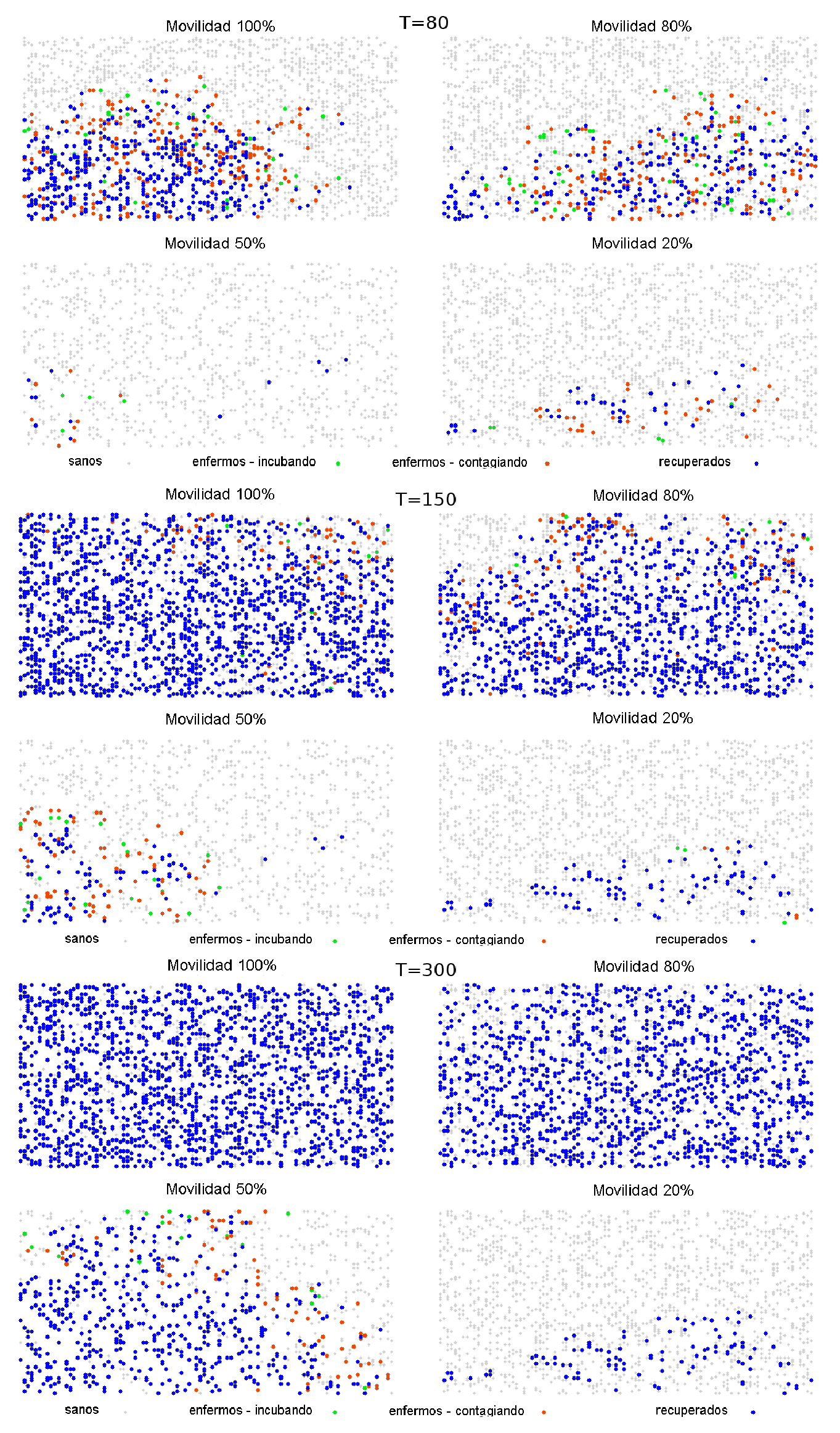
Figure 6: Evolución temporal de la red superficial durante la propagación de la infección en la población para diferentes porcentajes de movilidad en el sistema.

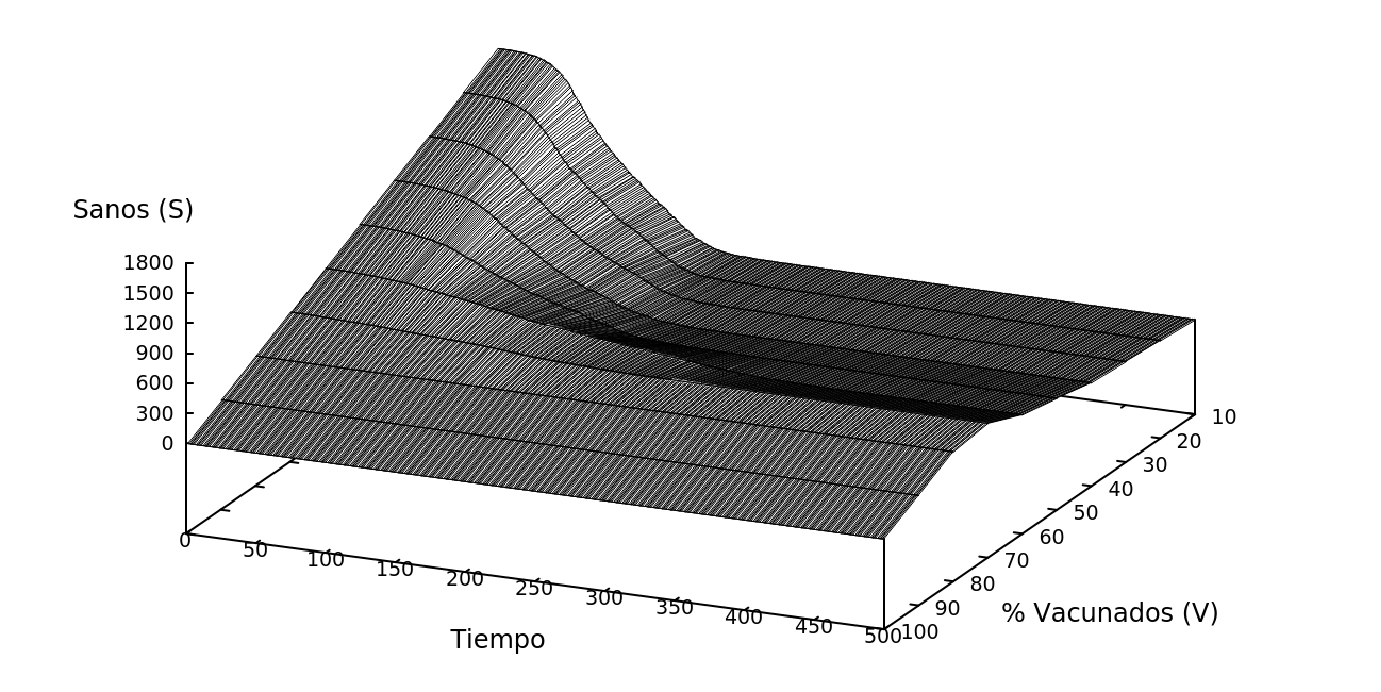
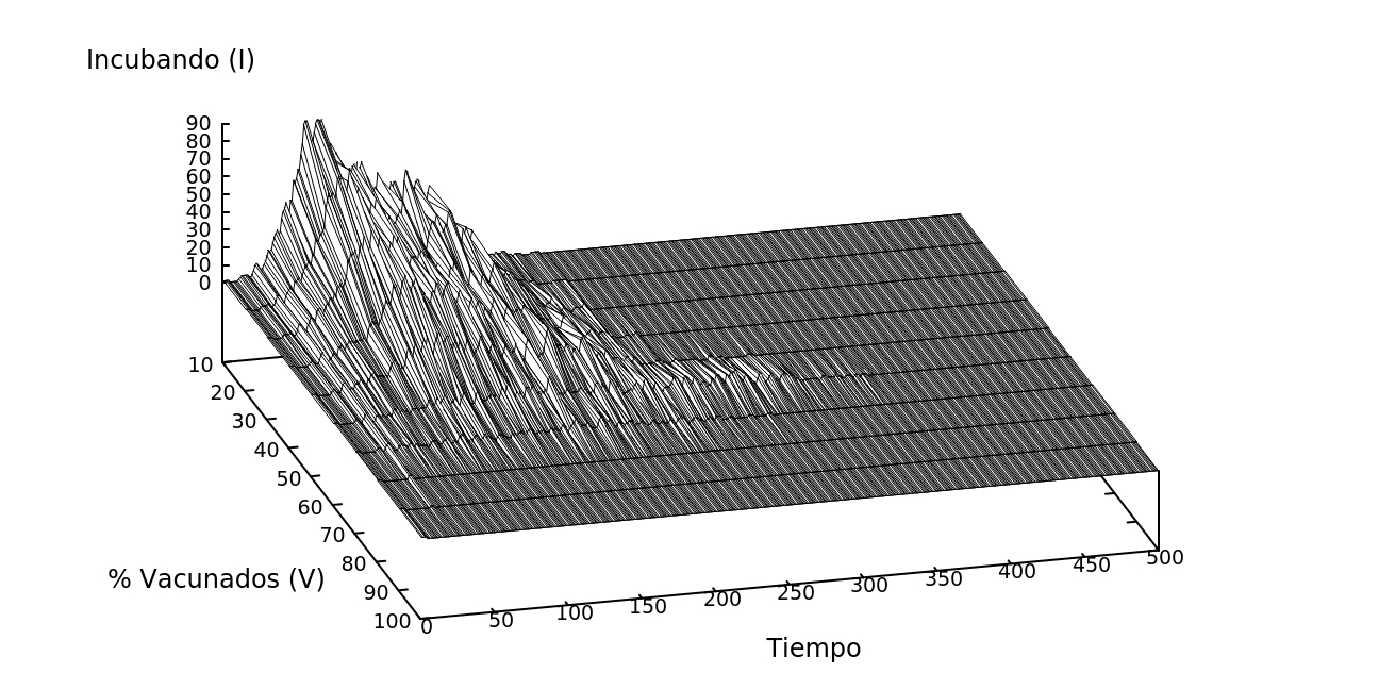
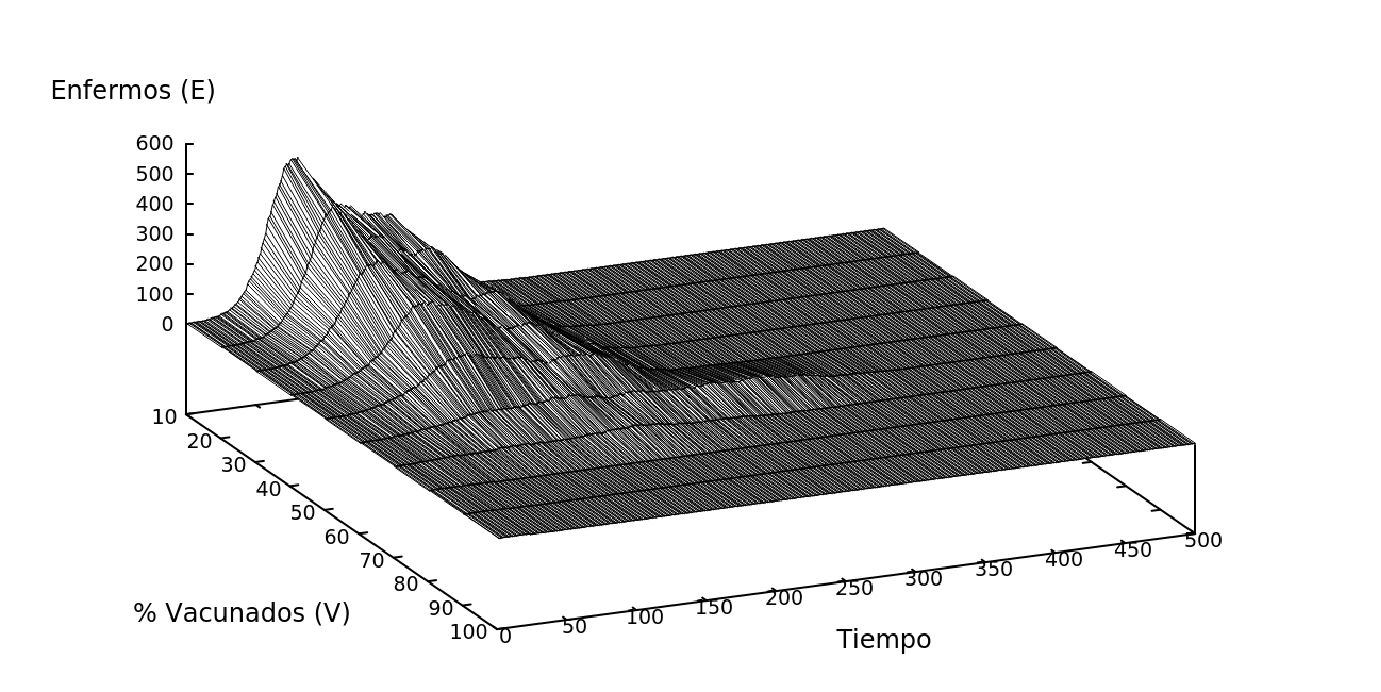
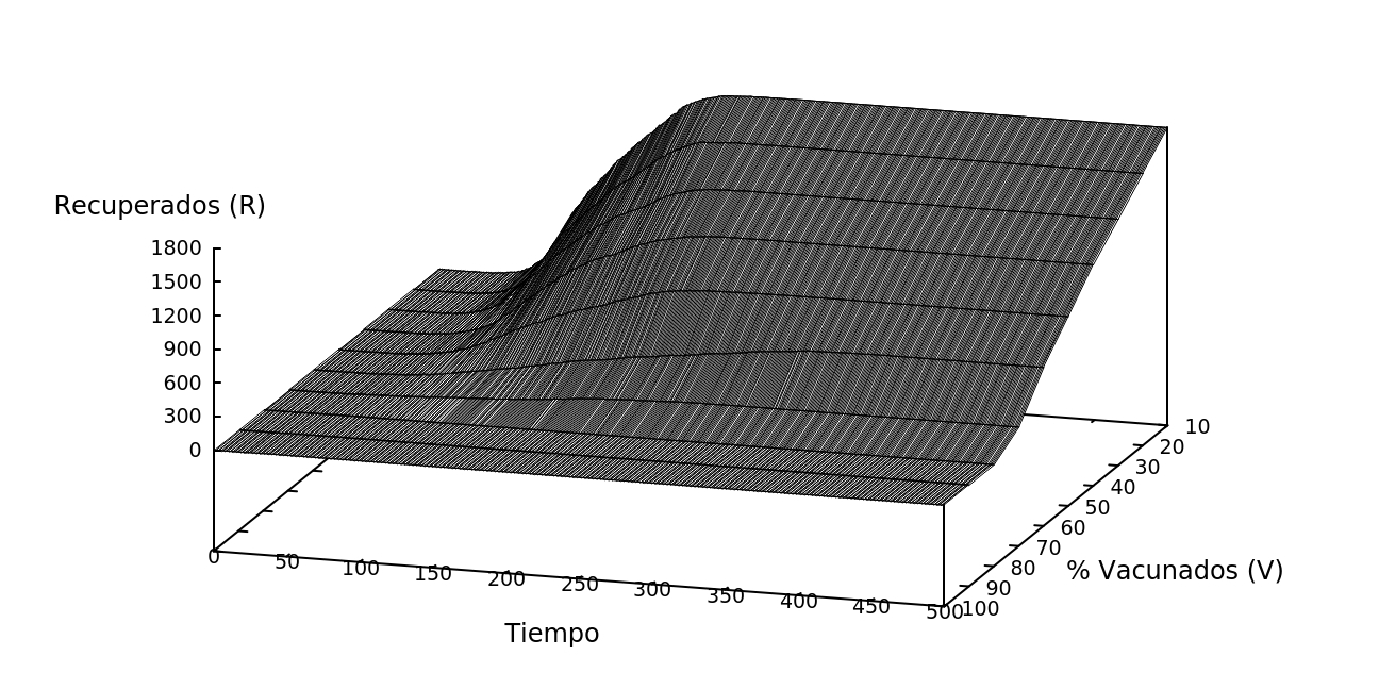
Figure 7: Dinámica del modelo con individuos N=2000, en una matriz de L=100, variando el porcentaje de individuos vacunados (0% - 100%).

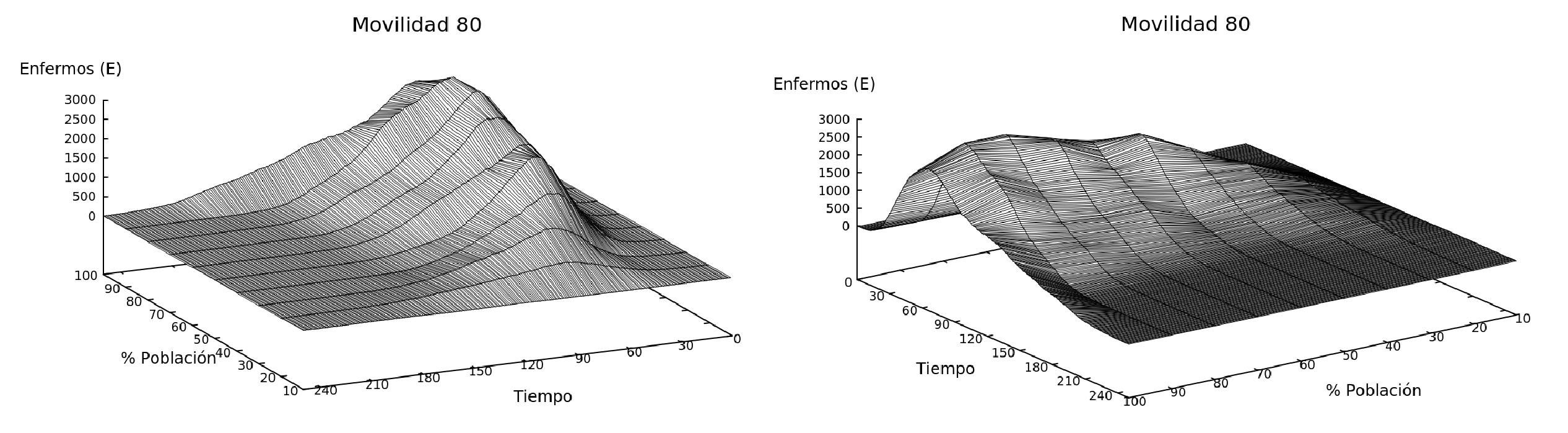
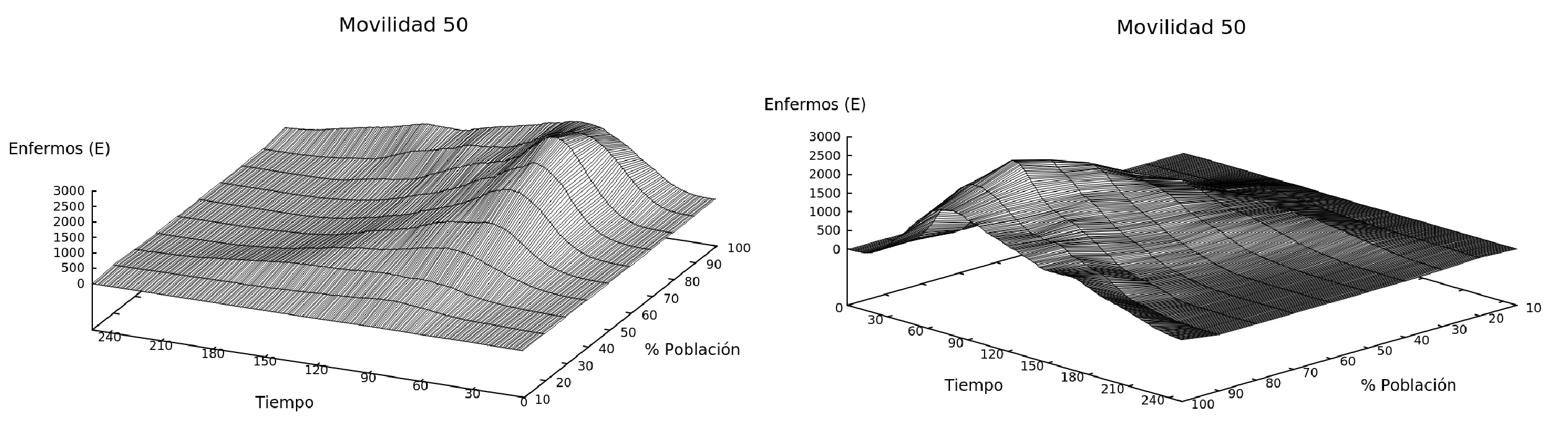
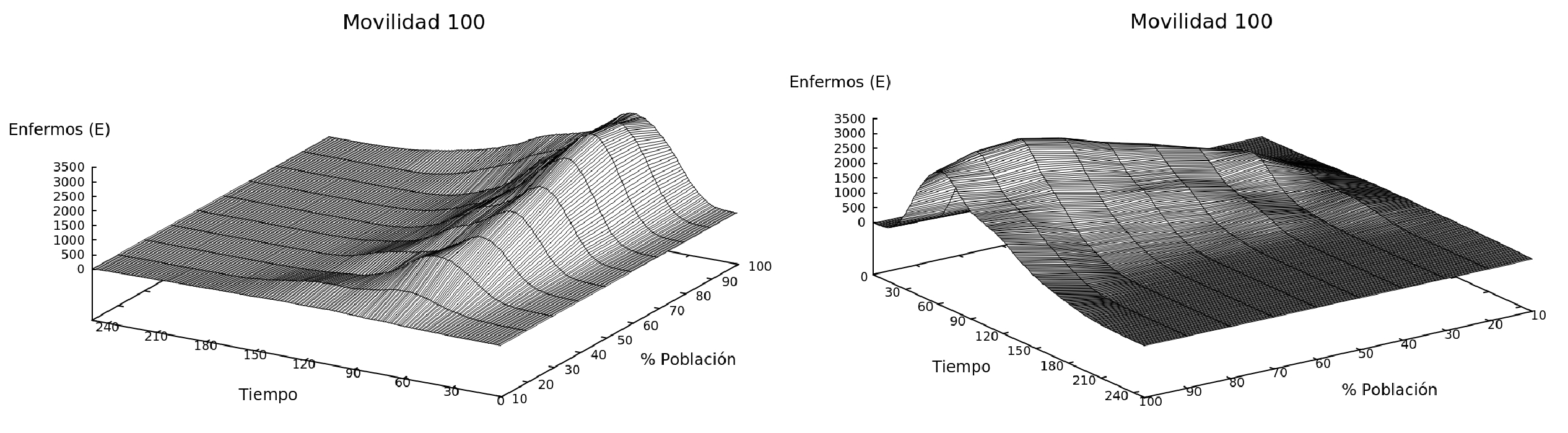
Figure 8: Las tres gráficas muestran la cantidad de enfermos que hay en el sistema en función del tiempo y de la variación de la población en el sistema para tres movilidades diferentes (50, 80 y 100 %).

Figure 9: Tiempo del sistema para alcanza el pico máximo de contagio para cada población, en función de la población total en el sistema, para diferentes movilidades (100, 80, 50%).

3.2  Variación del porcentaje de individuos vacunados en el sistema

En este modelo se mantuvo la movilidad del sistema al 100% (es decir todos los individuos se mueven al mismo tiempo) y se vario la cantidad de indivuos vacunados desde 0% hasta 100%, Fig. 7.

3.3  Variación de la población en el sistema

En este escenario el modelo tiene un tamaño constante L=100, pero se cambia el número de individuos y la movilidad del sistema, Fig. 8.

Con ayuda de estas gráficas, podemos calcular en que tiempo el sistema alcanza el pico máximo de contagio para cada población (variando la población desde el 10% hasta el 100%) y realizamos una curva para cada movilidad, como se observa en la Fig. 9.

Los comentarios de cada una de las figuras se dejan para la siguiente sección, describiendo las tres variaciones del modelo: movilidad, inclusión de población vacunada y variación de población en un sistema de tamaño constante.

 

4  Discusión

4.1  Acerca de la variación de movilidad en el sistema

El sistema se enfoca en superficies pequeñas ocupadas con el 20% de habitantes. Los resultados de la Fig. 4, muestran que sistemas con mayor movilidad presentan picos de enfermedad elevados en tiempos menores, en relación a los sistemas con menor movimiento.

En la Fig. 4(a) tenemos un sistema en el que todos los habitantes se mueven al mismo tiempo y el resultado es que el pico de enfermedad es del 33% en función a la población total; este es un sistema catastrófico debido a que ningún sistema de salud podría soportarlo. En la Fig. 4(b), solo el 80% de los individuos se mueven en el sistema y el resto permanece en reposo, en este escenario el pico máximo de contagios corresponde al 30% de la población, valor aun elevado para cualquier sistema de salud. En la Fig. 4(c) la movilidad del sistema es del 50% y el pico de enfermedad corresponde al 9% de la población total, obteniendo un valor menor a los escenarios anteriores, mismo que todavía es elevado para un sistema de salud. Finalmente, la Fig. 4(d) tiene una movilidad del 20% de la población en el sistema, alcanzando el pico de enfermedad a un 2% de la población total, demostrando que a menor movilidad, menor el porcentaje de contagios.

Se puede comprobar los resultados de las Fig. 4 observando la evolución temporal del sistema en la Fig. 6, en la cual se observa las variaciones temporales para los cuatro casos de movilidad. Efectivamente los sistemas de movilidad del 100% y el de 20% muestran los escenarios con mayor disparidad para un mismo tiempo. En el caso de movilidad del 100% la mayoría de los habitantes ya enfermaron y recuperaron de la enfermedad para un T=80, sin embargo, en el caso del 50% ni la mitad de la población se encuentra infectada en T=80, finalmente el caso de 20% de movilidad muestra una población ya recuperada en su totalidad en T=200 con una baja tasa de contagios.

Se observa que la variación temporal para las gráficas de la Fig. 5, que representan movilidades del 100% y 80% de la población, no exponen una diferencia sustancial, como los sistemas de 50% y 20% de movilidad. En la Fig. 5(a) se alcanza el pico a los 90 pasos, para la Fig. 5(b) se llega al pico a los 80 pasos, en la Fig. 5(c) el pico se alcanza a los 160 pasos y en la Fig. 5(d) llegamos al pico de contagio a los 80 pasos. Este último resultado, corresponde a un sistema en el que se elimina rápidamente el contagio debido a la baja movilidad del sistema, lo cual es bastante ideal.

Por lo mencionado, se demuestra en el sistema utilizado que cuando existe una menor interacción entre los individuos de una población, la misma sufre una tardía infección y de esta manera el sistema de salud puede actuar eficazmente contra la baja cantidad de enfermos, siendo esta la finalidad de las medidas de restricción impuestas en las diferentes regiones del mundo, sin embargo la desventaja de la menor movilidad es que el pico de contagio se extiende durante un periodo de tiempo mayor que los diferentes escenarios.

4.2  Acerca de la variación de individuos vacunados en el sistema

Una mejor alternativa a los sistemas de restricción es proporcionar una vacuna a la población. Los resultados de la Fig. 5(c) muestran que para el sistema con 50% de movilidad el contagio máximo es del 9% de la población, sin embargo en el sistema con vacunas, Fig. 7, observamos que si el 50% de la población está vacunada el pico de contagios es del 7%. De la misma forma para el sistema con una movilidad de 20% el contagio máximo obtenido es de 2%, mientras que en el caso en el que el 20% de la población no está vacunada el contagio máximo es de 0,02%. Efectivamente el resultado del sistema que considera la vacuna es más eficiente que el sistema que varía la movilidad. También se observa que la reducción del pico máximo de enfermos, es lineal en función a la cantidad de individuos vacunados en el sistema.

4.3  Acerca de la variación de la población en el sistema

En el sistema utilizado es posible variar el número de individuos que hay en la matriz, esto con la finalidad que el sistema pueda adaptarse a las nuevas disposiciones tomadas por los distintos gobiernos, entre ellas: reabrir los establecimientos de recreación, ferias y fronteras.

En la Fig. 9, se muestra un gráfico donde se cambia la cantidad de individuos en el sistema y se evidencia los tiempos en que se alcanza el pico con ayuda de la Fig. 8(a), (b) y (c). Podemos observar que cuando la población es menor, el tiempo en el que se llega al pico también es menor a comparación de un sistema lleno. Asimismo, observamos algo interesante en la primera parte del gráfico, en sistemas donde la población es pequeña y la movilidad reducida (Fig. 9, caso del 50% de movilidad), la enfermedad desaparece rápidamente. Este es un sistema ideal, debido a que la población cumple con un distanciamiento social riguroso, cumple con las medidas de cuarentena y además se tiene un n"umero de individuos pequeño (Fig. 9, para poblaciones de 10, 20 y 30%). Sin embargo para sistemas más reales (poblaciones mayores), la simulación confirma la importancia del distanciamiento social, debido a que para sistemas con mayor movilidad y mayor población los tiempos en los que se alcanza el pico son menores.

 

5  Conclusiones

Resultados obtenidos en el modelo de autómata celular para la propagación del Covid-19 muestran que los dos factores más relevantes para un contagio masivo, son la movilidad de una población y el incremento de habitantes en lugares cerrados. En el modelo se utilizó cinco grupos de interés, descartando la mortalidad, debido a la baja tasa que esta presenta, comparado con los otros grupos de interés en la investigación, lo cual modificaría únicamente los valores de la población recuperada, disminuyendo este último un porcentaje mínimo.

En sistemas donde la movilidad de los habitantes es reducida, se alcanza el pico de contagio en un periodo de tiempo similar al caso de máxima movilidad; lo cual no implica que sean iguales, debido a que el porcentaje de población infectada para ese tiempo no es la misma. En el caso de movilidad reducida, el modelo muestra que se elimina rápidamente la propagación del virus y que no toda la población consigue infectarse, sin embargo en el caso de movilidad máxima, más del 95% de la población contrae la enfermedad. Estos son los dos escenarios extremos, el primero en el que se acata una cuarentena rígida y solo el 10% de la población se mueve con bastante distanciamiento frenando la propagación rápidamente, y el segundo caso en el que no se toma ninguna medida de restricción y todos los habitantes salen al mismo tiempo. Los casos más reales corresponden a los valores intermedios de movilidad, 50%, 40% y 30% de movilidad, observando que el contagio se da paulatinamente; otorgando un plazo idóneo al sistema de salud, con el objeto de evitar el colapso de los mismos, equipar nosocomios y controlar la propagación de la pandemia.

Por otro lado el segundo factor de interés es la cantidad de habitantes en espacios cerrados, si tenemos muchos habitantes en espacios cerrados y pequeños, los niveles de contagio son mayores que en el caso de espacios con pocos habitantes ya que en el primer sistema, los individuos estarán en contacto continuo un determinado tiempo, en cambio en el segundo caso la probabilidad de contagio es menor debido al distanciamiento que se genera al tener pocos habitantes.

Por ultimo una alternativa más eficiente que las restricciones de movilidad y el distanciamiento social es implementar una vacuna 100% eficaz en una población. Si se vacuna al 50% de la población el pico máximo de contagios no llegaría a colapsar los centros médicos y los resultados son aún más favorables si se llega a vacunar a la mayoría de la población. Según los resultados obtenidos, vacunar al 70% de la población eliminaría casi por completo este problema ya que el pico de contagio máximo sería del 2% dejando sin relevancia ya los sistemas de restricciones. Se agradece profundamente a Bryan Vargas, quien contribuyó con un código para la elaboración de vídeos en gnuplot.

Conflicto de intereses Los autores declaran que no hay conflicto de intereses con respecto a la publicación de éste documento.

 

References

[12006Aguilera]

Aguilera, F. 2006, GeoFocus. Revista Internacional de Ciencia y Tecnología de la Información Geográfica, 81         [ Links ]

[22016Banisch]

Banisch, S. 2016, Markov Chain Aggregation for Agent-Based Models (Springer International Publishing)         [ Links ]

[32020Bohórquez et al.Bohórquez, Deisy Marcela Muñoz Morales, Arrieta, Prieto, Alarcón, & Unidad Investigación Usta]

Bohórquez, S. J. C., Deisy Marcela Muñoz Morales, Arrieta, C. A. R., Prieto, A. T. Z., Alarcón, O. M. G., & Unidad Investigación Usta. 2020         [ Links ]

[42016Cano & Rojas]

Cano, A. & Rojas, Á. 2016, UNIÓN. Revista Iberoamericana de Educación Matemática, 46, 33         [ Links ]

[52020Cruz et al.Cruz, Santos, Cervantes, & Juárez]

Cruz, M. P., Santos, E., Cervantes, M. V., & Juárez, M. L. 2020, Revista Clínica Española         [ Links ]

[62020Echeverri et al.Echeverri, Cabrera, & Echeverri]

Echeverri, M. G., Cabrera, A. M., & Echeverri, P. G. 2020, TecnoLógicas, 23, 129         [ Links ]

[72013Fresnadillo Martínez et al.Fresnadillo Martínez, García-Sánchez, García-Merino, del Rey, & García-Sánchez]

Fresnadillo Martínez, M. J., García-Sánchez, E., García-Merino, E., del Rey, Á. M., & García-Sánchez, J. E. 2013, Revista Española de Quimioterapia, 26         [ Links ]

[82020Ghosh & Bhattacharya]

Ghosh, S. & Bhattacharya, S. 2020, Applied Soft Computing, 96, 106692         [ Links ]

[92020Gutiérrez-Aguilar et al.Gutiérrez-Aguilar, Córdova-Lepe, Muñoz-Quezada, & Gutiérrez-Jara]

Gutiérrez-Aguilar, R., Córdova-Lepe, F., Muñoz-Quezada, M. T., & Gutiérrez-Jara, J. P. 2020, Medwave, 20, e7871         [ Links ]

[102020Locht]

Locht, C. 2020, Anaesthesia Critical Care & Pain Medicine, 39, 703         [ Links ]

[112020Medina et al.Medina, Jaramillo-Valverde, et al.]

Medina, R. M., Jaramillo-Valverde, L., et al. 2020

[122020Organización Mundial de la Salud]

Organización Mundial de la Salud. 2020, https://www.who.int/es/news/item/27-04-2020-who-timeline-covid-19        [ Links ]

[132020Wang et al.Wang, Pan, Wan, Tan, Xu, Ho, & Ho]

Wang, C., Pan, R., Wan, X., Tan, Y., Xu, L., Ho, C. S., & Ho, R. C. 2020, International Journal of Environmental Research and Public Health, 17, 1729         [ Links ]