Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Boliviana de Física
versión On-line ISSN 1562-3823
Revista Boliviana de Física v.36 n.36 La Paz nov. 2020
B. CONTRIBUCIONES Y REVISIONES
Estudio del método Monte Carlo en simulaciones para la estimación del valor de π
Study of the Monte Carlo method in simulations for the estimation of the π value
J. C. Vargas † , Carlos Andrés Cruz-Carpio † †
Carrera de Física, Universidad Mayor de San Andrés
Campus Universitario, c. 27 Cota-Cota, Casilla de Correos 8635 La Paz - Bolivia
† jcrespo+rbf@fiumsa.edu.bo
† † ccruz@fiumsa.edu.bo
Resumen
En este artículo se presenta los resultados de tres metodologías diferentes en las que se aplicó una simulación Monte Carlo para estimar el valor de π: el método de comparación de áreas, el método propuesto por Buffon y la extensión de Laplace al método de Buffon. Se estudió con detalle el resultado no determinista de las simulaciones y se demostró que cumplen con los teoremas fundamentales de la probabilidad. Los tres casos se desarrollaron en un lenguaje de programación de alto nivel: Python, junto con la librería Numpy que le otorga una performance optimizada.
Descriptores: Educación - métodos Monte Carlo - simulaciones.
Código(s) PACS: 01.40.-d, 02.70.-c, 05.10.Ln
Abstract
This article presents the result of three dierent methodologies that estimate the π value using the Monte Carlo’s simulation: the comparative area’s method, the method proposed by Buffon and the Laplace’s extension. The three cases were developed in Python – a high level language and Numpy library which give it an optimized performance. The non-deterministic result of the simulations was studied in detail and it was shown that they comply with the fundamental theorems of probability.
Subject headings: Education - Monte Carlo methods - simulations.
1 Introducción
El método de Monte Carlo tiene un génesis moderno en el trabajo pionero de Stan Ulam y John Von Neumann. Luego de la segunda Guerra Mundial aplicaron distintos métodos de Monte Carlo en simulaciones para el desarrollo de armas termonucleares. Desde entonces y por más de 50 años que se aplicaron estos desarrollos en la investigación y perfeccionamiento de distintos métodos que modelan el transporte de neutrones y radiación gamma con bastante éxito experimental como menciona [22001Bielajew ].
Hoy resulta una alegre ironía que ningún producto que haya aplicado la metodología Monte Carlo en su desarrollo, se haya empleado en conflicto alguno. Más aún los científicos han explotado el uso de simulaciones Monte Carlo para obtener un beneficio público positivo aplicándola en salud. Por ejemplo, los planeamientos de dosis en radioterapia dependen actualmente en algún grado de cálculos obtenidos mediante simulaciones que emplean Monte Carlo. El método de Monte Carlo es un método de resolución numérica donde se modelan las relaciones e interacciones de distintos objetos y su entorno, mediante la generación aleatoria de estas interacciones. Mientras mayor sea la repetición de pruebas se obtiene un resultado que va convergiendo a un valor con mayor precisión. Es por el recurso de la aleatoriedad que obtiene el nombre Monte Carlo, pues se inspira en la región del Principado de Mónaco donde se encuentran el casino Monte Carlo.
Un método Monte Carlo se puede definir de la siguiente forma:
"Los métodos Monte Carlo son aquéllos en los que las propiedades de las distribuciones de las variables aleatorias son investigadas mediante la simulación de números aleatorios. Estos métodos, dejando a un lado el origen de los datos, son similares a los métodos estadísticos habituales en los cuales las muestras aleatorias se utilizan para realizar inferencias acerca de las poblaciones origen. Generalmente, en su aplicación estadística se utiliza un modelo para simular un fenómeno que contiene algún componente aleatorio. En los métodos Monte Carlo, por otro lado, el objeto de la investigación es un modelo en sí mismo, y se utilizan sucesos aleatorios o pseudoaleatorios para estudiarlo".[32006Gentle ]
El método cobra una especial relevancia las últimas décadas debido a que se produjeron sustanciales y significativos avances respecto a la potencia de los procesadores y las distintas arquitecturas informáticas. Es ampliamente usado en problemas donde obtener un resultado analítico no es posible, o en problemas que contienen demasiada complejidad (como es el caso de la ecuación de transporte de Boltzmann para partículas sin carga).[22001Bielajew ]
2 Marco Teórico
El estudio matemático formal del azar se remonta hace bastantes siglos. En 1654 motivados por dos problemas propuestos por Antoine Gombaud (le Chevalier de Méré), basados en las observaciones de los juegos de azar de la época, es que se reúnen a resolver el desafío matemático personalidades como Pascal, Cardano y Fermat entre otros dando inicio a la teoría clásica de la probabilidad. Es en este periodo que distintos matemáticos advierten la relación de la teoría combinatoria y la incipiente teoría de la probabilidad.
Un matemático que realiza un interesante aporte en este aspecto es Leibniz, el cual luego de realizar la disertación titulada Dissertatio de Arte combinatoria, encuentra particular interés por ‘la certidumbre’.
La probabilidad para Leibniz es un criterio objetivo de verdad. Es una lógica de lo contingente (que puede suceder o no) que se contrapone a la lógica de lo necesario. Permitiendo a la probabilidad alcanzar la verdad. El interés de Leibniz por los juegos iba más allá de la teoría de la probabilidad, sus aplicaciones podrían aplicarse al Arte de Inventar y subsecuentemente a la construcción de las características universales, temas que le parecían de mayor interés que a otros autores.[11993Charles ]
2.1 Experimentación y la teoría de probabilidad
En 1777, el naturalista rancés, el conde de Buffon (1707−1788) propuso el primer experimento que utilizaba un método de Monte Carlo, pues dependía de un hecho completamente aleatorio: la caída de una aguja luego de lanzarla. Las agujas son lanzadas aleatoriamente en un piso con un patrón de rayas separadas una cierta distancia. Buffon considero que los centros están uniformemente distribuidos en un piso infinito. Las agujas no ruedan a las aberturas como lo harían en la vida real, ni estas interactúan entre si. Además, el ángulo respecto a la horizontal es considerado distribuido uniforme entre 0 y π/2.
El resultado al que se llegó relaciona la probabilidad de cruzar una de las rayas con la distancia de separación, la longitud de la aguja y el valor de π. Esta se expresa en la Ec.1.
![]()
Se conoce como la extensión de Laplace al problema de Buffon cuando se considera tanto líneas verticales como horizontales. Se llama Buffon-Laplace aunque Buffon, quien resolvió este problema anteriormente contenía un error que más tarde en 1812 fue corregido por Laplace expresándose en la Ec. 2.
![]()
De esta propuesta, se pretende obtener el valor de π. La probabilidad se obtiene empóricamente al realizar el experimento un número grande de veces y contar cada caso. Este problema histórico fue estudiado en ese entonces como una curiosidad poco práctica, debido a que obtener un resultado preciso requería un número grande de repeticiones. Durante el siglo XX, con el advenimiento de las nuevas tecnologías es que el método de Monte Carlo vuelve a cobrar relevancia pues permite un número grande de repeticiones sin complicación. Sin embargo el manejo teórico de la matemática involucrada es bastante conocido, se realiza una breve revisión.
2.2 Teorema de los Grandes Números
Sea X1,..., Xn una sucesión de variables aleatorias, diremos que la sucesión de Xn converge en probabilidad a X (que es otra variable aleatoria), si solo si para todo ∀ε > 0:
lim (P[(Xn − X) > ε]=0)(3)x → ∞
Siendo conocida esta expresión como criterio de convergencia débil. Tomamos la variable aleatoria de interés, el promedio: ―x=[1/(n)]∑Xi Aplicando el operador lineal Esperanza:
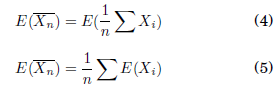
Si consideramos que la sucesión de variables Xi son independientes e idénticamente distribuidas, la Esperanza para cada variable es la media μ.
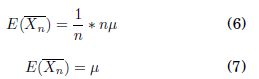
Esta relación nos muestra que el valor esperado del promedio de una muestra tiende al valor medio. De igual manera con el operador varianza tenemos:
![]()
Con el supuesto de las variables (Xi), son independientes e idénticamente distribuidas, la varianza de la suma, es la suma de las varianzas:
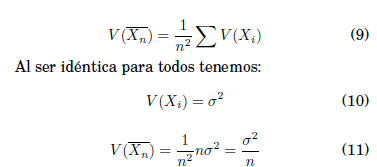
Con los resultados de la esperanza y varianza del promedio, se puede enunciar el siguiente teorema: Sea Xn una sucesión de una variable aleatoria independiente e idénticamente distribuida tal que E(Xi2 ) < ∞∀i ,y:
E(Xi)=μ (12)
V(Xi)=σ2 (13)
Entonces el promedio de la secuencia Xn converge en probabilidad a μ. Es decir que para una población que tiene una media μ, si se toma una muestra y se calcula el promedio muestral, este tiende al valor de μ mientras n tienda a ∞. Esto se demuestra al tomar un valor ε > 0, entonces, usando la relación de acotación de Chemichev:

Mostrando que cuando n tiende a un número grande, la probabilidad se anula y por consecuencia el promedio converge en probabilidad a μ.
2.3 Teorema del Limite Central
Sea X1,..., Xn una sucesión de variables aleatorias, independientes e idénticamente distribuidas tales que ∀i tengan el segundo momento finito E(Xi2) < ∞ con una media ∞ y una varianza σ2 distinta de cero. Entonces, si n es suficientemente grande, la variable aleatoria promedio:
![]()
Tiene aproximadamente una distribución normal con:

El teorema central de la probabilidad tiene una importancia categórica al ser enunciada para una sucesión de variables con cualquier distribución.
3 Modelo de Simulación
3.1 Entorno de desarrollo
Como quedo manifiesto en el anterior punto el método Monte Carlo tiene una precisión proporcional a [1/(√N)]. En comparación con otros métodos numéricos determinósticos (como por ejemplo el método de trapecios o Simpson para encontrar la integral de una función definida) que tienen un error de aproximación proporcional a [1/(N2)] en el mejor de los casos, los métodos que aplican Monte Carlo (como por ejemplo la integración por Monte Carlo) requieren una cantidad considerable mayor de datos a procesar. Sumado este hecho a la complejidad que puede involucrar el modelamiento de las interacciones aleatorias, es que generalmente se prefiere usar lenguajes de programación de bajo nivel que permitan optimizar el tiempo de cómputo total.
Por ejemplo, es común encontrar desarrollos en C, C++ y fortran entre otros. Existiendo hoy libreríos que facilitan la generación de números pseudoaleatorios y el manejo matemático. Aún con esta ventaja el código necesario para una aplicación final suele ser bastante complicado y extenso. Estos dos criterios identificados se consideraron para la selección del entorno de desarrollo:
-
El tiempo de procesamiento
-
La legibilidad y simplicidad del código
Siendo Python un lenguaje de alto nivel que cumple con el segundo criterio, al incluir la librería Numpy (librería de procesamiento numérico para Python) obtenemos una velocidad de procesamiento comparable a C. Adicionalmente se utilizó una librería para la representación de los datos, Matplotlib. Se detalla todo el código y las dependencias en el repositorio del proyecto: https://github.com/CobraPython/montecarlopi
3.2 Generación de números pseudeoaleatorios
Existen distintos métodos para la generación de números aleatorios, sin embargo, la generación de estos en ordenador parte necesariamente desde una semilla (seed) que es un valor concedido por el usuario. Con esta semilla se genera una única serie de números aleatorios, pudiendo ser replicados a partir de esta. Por esta razón es que se denominan números pseudo aleatorios. La librería Numpy utiliza el algoritmo Mersenne Twistter (MT19937) escribe [62019Marchand ] para la generación de números pseudoaleatorios. Este método particular tiene la cualidad de tener una periodicidad bastante grande en la generación de números: 219937−1 [51998Makoto ].
3.3 Métodos de estimación de π
3.3.1 Método Simple para la estimación de π
Se propone estimar el número de π con el siguiente modelo: Consideramos un cuadrado de lado L, con una circunferencia en su interior de radio L. La relación de áreas se da en Ec. 19:
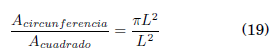
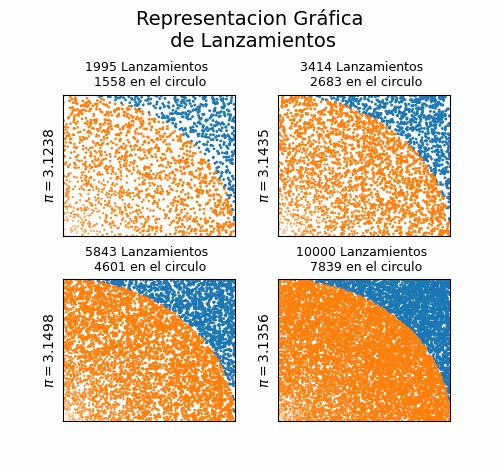
figure 1: Representación gráfica de la estimación de π mediante el lanzamiento aleatorio de puntos. Mientras mayor sea el número de lanzamientos las áreas son más definidas
Una forma de calcular esta relación de áreas es lanzar al azar puntos dentro del cuadrado. Estos puntos pueden quedar también dentro de la circunferencia, la relación de áreas quedara expresada por aquellos puntos que estén dentro del circulo sobre el total. En la fig. 1 se muestra un ejemplo del experimento propuesto, mostrando un solo cuadrante ya que las áreas son simétricas en cada eje.
Queda bastante ejemplificado que mientras mayor sea el número de puntos, las áreas quedan mejor definidas. Para obtener esta aproximación se necesitan generar los puntos aleatoriamente con una distribución uniforme, es decir, con igual probabilidad de caer dentro y fuera del área del cuarto de circunferencia.
3.4 Método de Buffon para la estimación de pi
En el caso de la estimación de π usando la propuesta experimental de Buffon y la extensión de Laplace, tenemos más variables aleatorias a considerar. Puesto que cada aguja cae aleatoriamente con un centro en (Xi,Yi), tiene relacionada otra variable aleatoria que corresponde al ángulo de inclinación θ de la aguja. La fig.2 nos muestra un ejemplo.
Si bien en este caso se recurre a una función trigonométrica para evaluar la inclinación y considerar a las agujas que cruzan la línea, el ordenador usa recursivamente el valor de π para calcular la función coseno, siendo este un error “histórico” ya que recurre al valor de π para calcular al mismo. Por esta razón se usó una corrección geométrica que evita el uso de unciones trigonométricas.
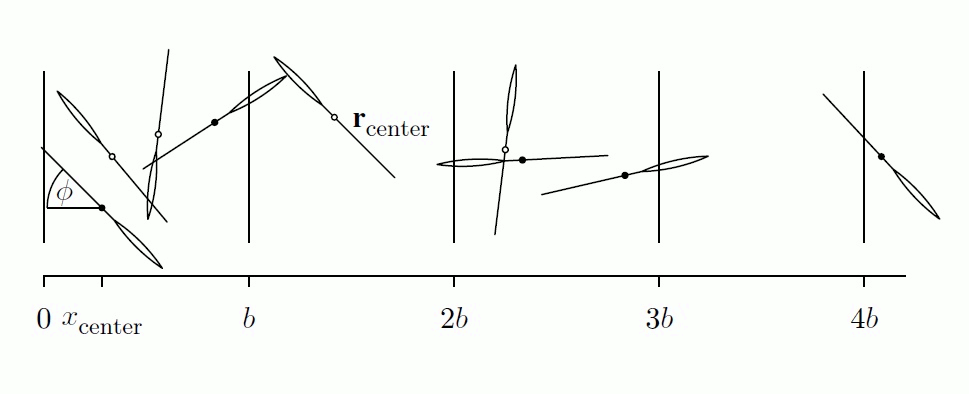
figure 2: Las agujas caen en una posición y ángulo aleatorio. Dependiendo de este ángulo se puede determinar si la aguja cruza una línea.[42006Krauth, Werner ]

figure 3: Representación gráfica del experimento de Buffon lanzando 2000 agujas.[42006Krauth, Werner ]
Pasando de requerir generar aleatoriamente un ángulo θ, a generar aleatoriamente desplazamientos δx,δy. En la siguiente Figura se muestra una representación gráfica de cómo se realiza la simulación con un número grande de lanzamientos aleatorios con distribución uniforme. [42006Krauth, Werner ] Para esta propuesta del lanzamiento de agujas para la estimación de π, se comparan dos casos:
-
Problema Buffon, cuando las agujas cruzan líneas en un solo eje.
-
Problema Buffon-Laplace, cuando las agujas cruzan líneas en sentido vertical y horizontal.
En la fig. 3 se puede ver el resultado del lanzamiento de 2000 agujas de largo a de la misma longitud que la separación de las lineas b, es decir que a=b. La probabilidad se calcula en relación a cuantas agujas cruzan una línea sobre el total de agujas.
4 Análisis de resultados
4.1 Método simple para la estimación de π
4.1.1 Comprobación del limite central
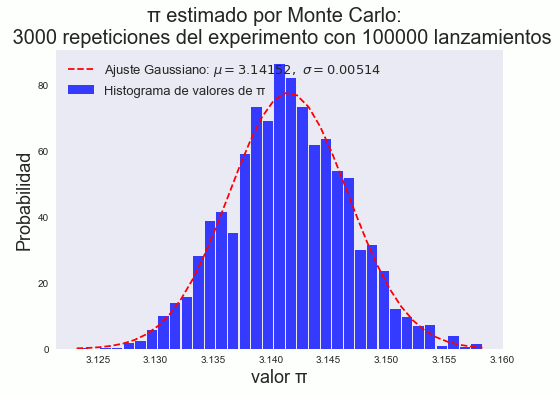
Se consideró el lanzamiento de 105 puntos y se repitió 102 veces el experimento, el histograma obtenido se muestra en la fig. 4. Al realizarse 3 ×103 veces el experimento, en la fig. 5 se nota más claramente que el histograma obtenido tiene un comportamiento gaussiano.
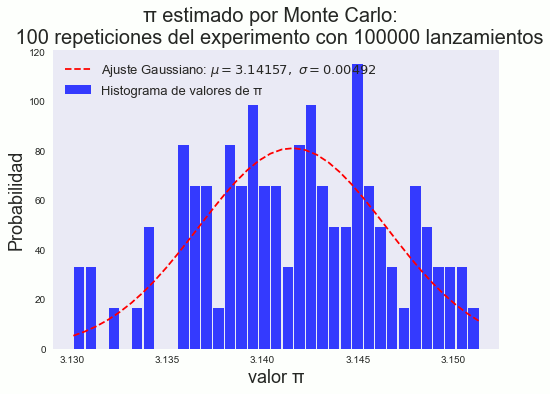
figure 4: Histograma del método simple para 100 repeticiones de 100000 lanzamientos.
figure 5: Histograma del método simple para 3000 repeticiones de 100000 lanzamientos. Se aprecia el comportamiento gaussiano, la característica forma de "campana".
Si se compara con el histograma de la fig. 6 al realizar 3 ×103 veces el experimento lanzando 106 puntos, el comportamiento del histograma es también claramente Gaussiano.
También se puede resaltar que el valor de σ es menor cuando consideramos 106 (σ = 0.00162) en comparación con 105 (σ = 0.00473).
4.1.2 Comprobación del teorema de los grandes números
Se ha estimado el valor de π para distintas cantidades de puntos generados. En la fig. 7 se muestra la congruencia de π con el valor que tiene la librería Numpy (IEEE 754 double-precision format). Se muestra que mientras mayor es el N tomado para estimar el valor de π, su error absoluto converge a cero.
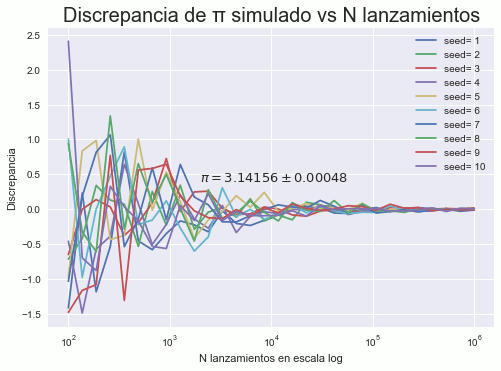
En la fig. 8 se muestra que este comportamiento es invariante al variar las semillas en la generación de losnúmeros pseudoaleatorios.
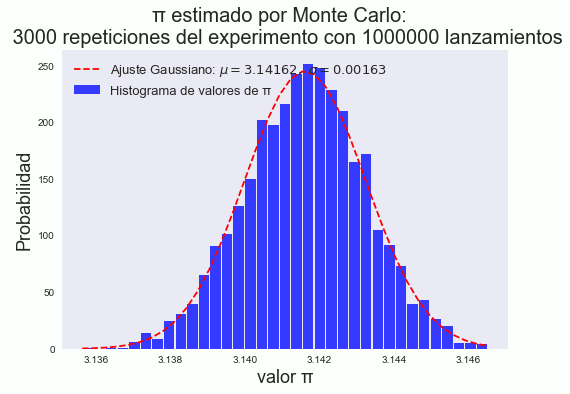
figure 6: Histograma del método simple para 3000 repeticiones de 1000000 lanzamientos. Se aprecia el comportamiento gaussiano, la característica forma de "campana".
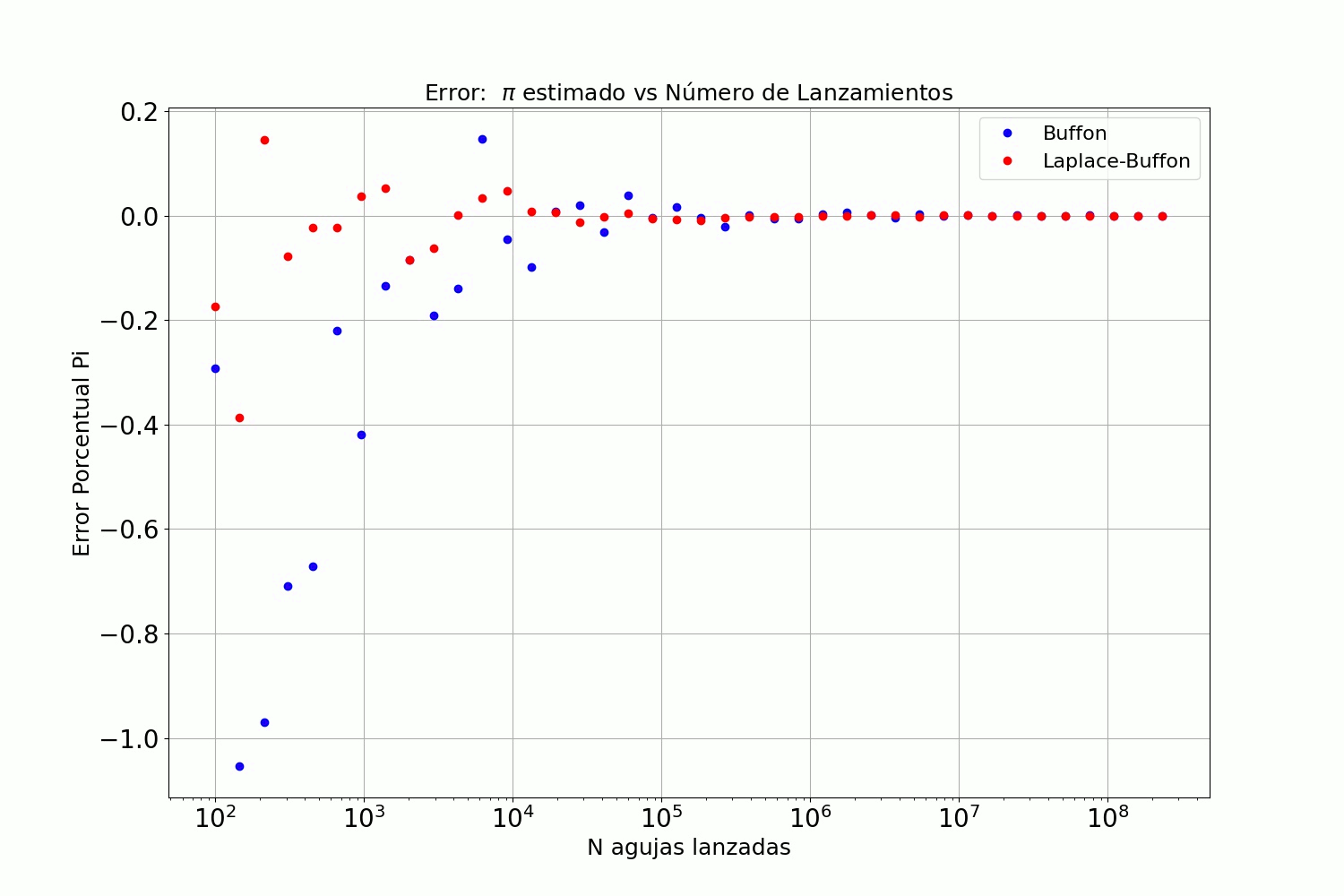
figure 7: Se comparan los errores de ambos métodos (Buffon y Buffon-Laplace). Se observa que los datos de Buffon-Laplace convergen a 0 con un menor N que los datos de Buffon.
figure 8: Error absoluto del valor de π a medida que N crece. Se observa que independientemente de la semilla representada por colores, el valor converge a 0.
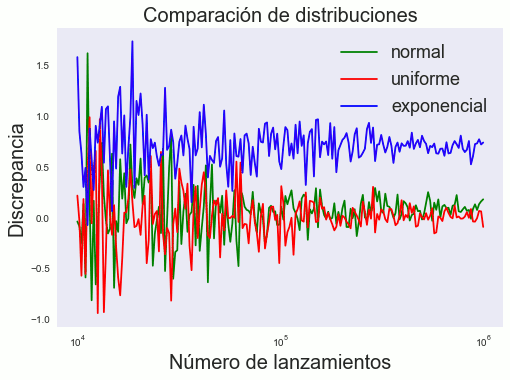
figure 9: En esta gráfica se comparan tres unciones de distribución de probabilidad (pd) que sigue el generador de números aleatorios. Con los debidos parámetros el valor converge a cero. Sin embargo, se aprecia que independientemente de los parámetros existe un valor de convergencia.
Finalmente, en la fig. 9 se muestra una comparativa de la discrepancia al estimar el valor de π si consideramos distintas distribuciones de probabilidad en la generación aleatoria de puntos. Se comparan tres distribuciones:
-
Normal
-
Uniforme
-
Exponencial
Es notable que para las tres distribuciones el valor de la discrepancia del valor estimado de π converge a un valor mientras mayor número de lanzamientos se utilice en la prueba. Al aplicar una distribución normal con μ = 0.27 y σ = 0.5 el valor estimado de π es cercano que cuando se aplica una distribución uniforme. Al aplicar una distribución exponencial con un parámetro λ = 0.42, el valor estimado de π converge con un error de más del 0.5. Esto se debe a que los lanzamientos de las agujas tienen mayor probabilidad de caer en cierta posición y ángulo, lo que puede equivaler de manera experimental a por ejemplo que las agujas tengan otra conformación física, como en la siguiente imagen.
Si realizamos los histogramas al estimar el valor de π en un número grande de repeticiones aplicando distintas distribuciones en la generación de puntos y ángulos de las agujas, se demuestra que invariantemente se tienen un comportamiento Gaussiano en todos los casos. En las figs. 11 y 10 se muestran los histogramas de las distribuciones normal y exponencial respectivamente.
4.2 Método de Buffon para la estimación de π
4.2.1 Comprobación del teorema del límite central
Se consideró el lanzamiento aleatorio de 2 \time 108 agujas con una distribución uniforme para la posición y ángulo, repitiendo el experimento 200 veces para ambos casos; Buffon y la extensión de Laplace.
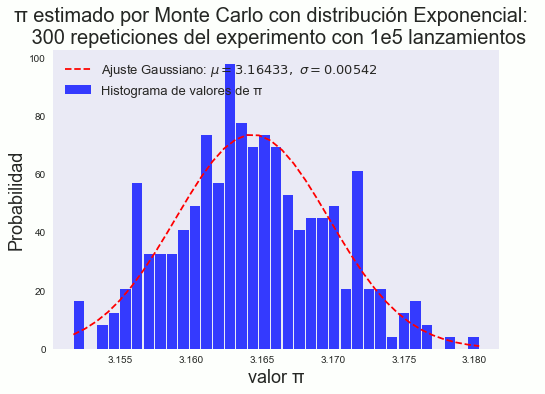
figure 10: Histograma de los datos que siguen una distribución exponencial. Se aprecia el comportamiento gaussiano.
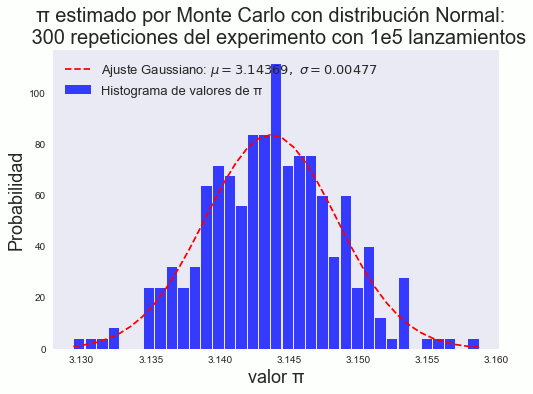
figure 11: Histograma de los datos que siguen una distribución normal. Se aprecia la forma característica de "campana".
Mostrando que el histograma de la fig. 12 de las estimaciones de Pi para ambos métodos presenta un comportamiento Gaussiano, demostrando la validez del teorema del límite central.
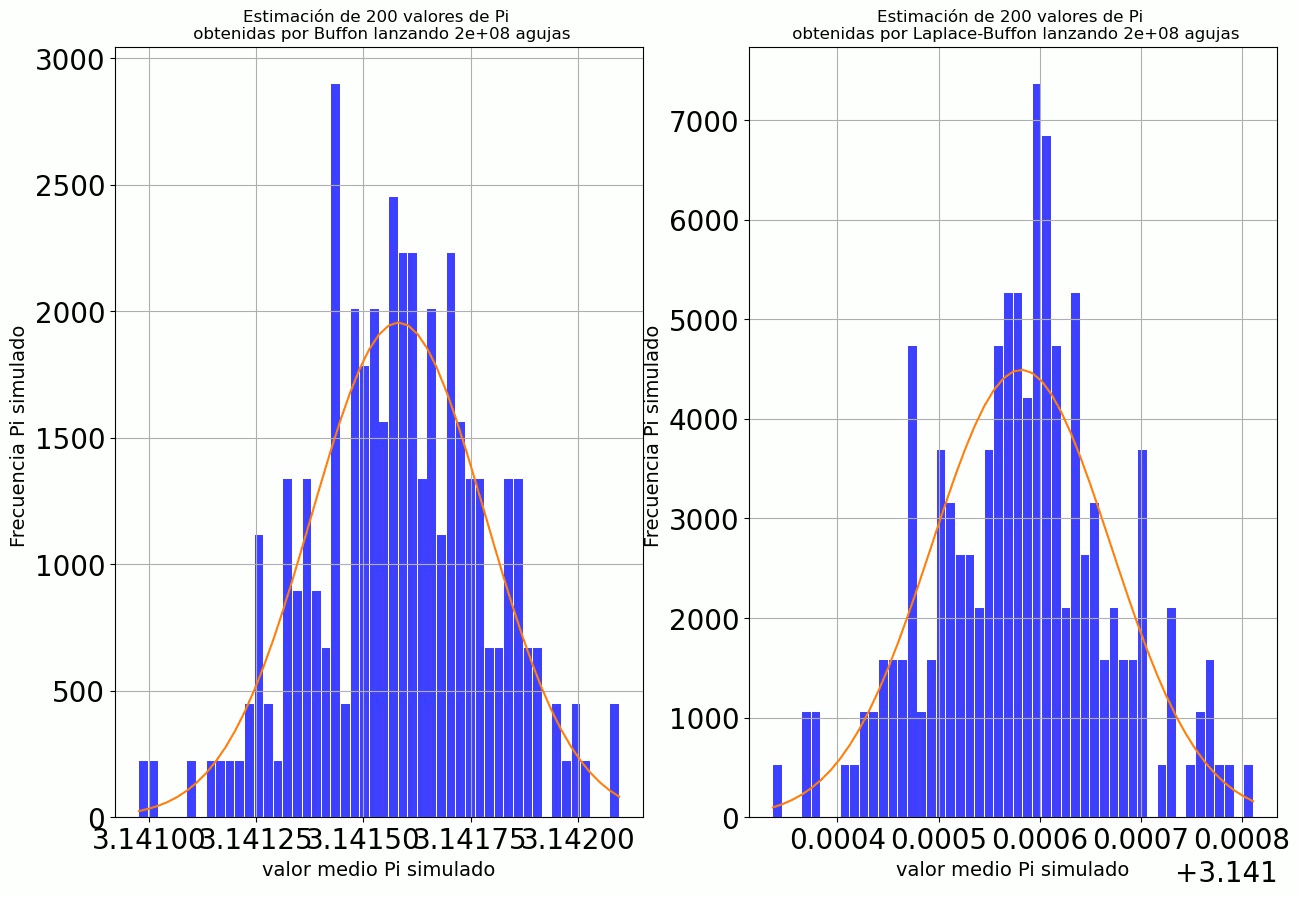
figure 12: Comparación histogramas. A la izquierda siguiendo el método de Buffon y a la derecha Buffon con la corrección de Laplace.
4.2.2 Comprobación del teorema de los grandes números
En la fig. 7 se resume el error porcentual al estimar el valor de π vs. el números de lanzamiento de agujas para ambos métodos. El error converge a cero a partir del lanzamiento de 106 agujas. También queda evidente que con el método corregido de Laplace el valor estimado de π converge a su valor esperado con un menor número de lanzamiento de agujas casi en un actor de 10 al compararlo con el método original de Buffon.
5 Conclusiones
En esta experiencia se mostraron tres distintos métodos que aplican Monte Carlo para estimar el valor de π: el método simple por comparación de áreas, el método propuesto por Buffon mediante el lanzamiento de agujas y el método de Buffon ampliado por Laplace.
Se demostró que los resultados obtenidos mediante una simulación Monte Carlo tienen un carácter no determinista que cumplen con los teoremas centrales de la teoría de la probabilidad.
Finalmente, se mostró que se puede lograr simulaciones con un alto costo computacional aplicando un lenguaje de alto nivel como Python y la librería Numpy, lo que permite tener un código simple y legible.
Conflicto de intereses Los autores declaran que no hay conflicto de intereses con respecto a la publicación de éste documento.
References
[Charles (1993)]
charles Charles M.(1993), Revista de la Sociedad Española de Historia de las Ciencias y de las Técnicas 16 241 [ Links ]
Bielajew A. (2001), Some random thoughts on Monte Carlo electron and photon transport (Springer) [ Links ]
Gentle J. (2006), Random number generation and Monte Carlo methods (Springer Science & Business Media) [ Links ]
Krauth, Werner (2006), Statistical mechanics: algorithms and computations (OUP Oxford) [ Links ]
Matsumoto, Makoto and Nishimura, Takuji (1998), ACM Transactions on Modeling and Computer Simulation (TOMACS) 1 3 [ Links ]
Marchand T. (2019), How Does Your Computer Generate Random Numbers? (https://www.sicara.ai/blog/2019-01-28-how-computer-generate-random-numbers) [ Links ]