Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
Compartir
Revista Boliviana de Física
versión On-line ISSN 1562-3823
Revista Boliviana de Física v.36 n.36 La Paz nov. 2020
B. CONTRIBUCIONES Y REVISIONES
Hamiltoniano Covariante para la partícula cargada
A Covariant Hamiltonian or a charged particle
V. M. Peñafiel† Leoncio Gómez ††
Instituto de Investigaciones Físicas, Universidad Mayor de San Andrés
Campus Universitario, c. 27 Cota-Cota, Casilla de Correos 8635
La Paz - Bolivia
†Email: vmiguel@fiumsa.edu.bo.
††Email: leongomezd@gmail.com.
Resumen
Se hace un análisis detallado del problema de una partícula cargada en un campo electromagnético, probando que es posible preservar la covariancia manifiesta en un tratamiento canónico riguroso bajo la teoría de Dirac para el formalismo hamiltoniano asociado a lagrangianas singulares.
Descriptores: formalismo Hamiltoniano y Lagrangiano - mecánica cuántica y relatividad especial - formalismo canónico.
Código(s) PACS: 11.10.E, 03.00.00, 04.20.Fy
Abstract
A detailed analysis o the problem of a charged particle in an electromagnetic field was carried out. It was proven that it is possible to preserve the manifest covariance in a rigorous canonical treatment under the Dirac theory or the Hamiltonian formalism associated to singular Lagrangians.
Subject headings: Lagrangian and Hamiltonian approach - quantum mechanics and special relativity - canonical formalism.
1 Introducción
El problema de obtener el hamiltoniano y las ecuaciones de movimiento canónicas cuando la función lagangiana es singular (su hessiana tiene determinante cero) no es trivial, pero la teoría al respecto está completa y es muy conocida (ver, por ejemplo, [51974Sudarshan & Mukunda]). En los casos relevantes, las complicaciones aparecen casi siempre al momento de encontrar, procesar y garantizar la estabilidad de las restricciones (especialmente las subsidiarias y auxiliares). Quizá eso explica el que, por ejemplo, un hamiltoniano manifiestamente covariante para la partícula relativista cargada, urgida por fuerzas electromagnéticas, tenga que ser introducida, a veces, completamente ad hoc ([21998Jackson]). El presente es un tratamiento completo de ese problema en forma manifiestamente covariante y siguiendo una línea rigurosa de razonamiento en el marco de la teoría de Dirac al efecto ([11964Dirac]). Previamente, una manera expedita de obtener información acerca de la estructura general de la dinámica relativista consiste en considerar una transformación general de coordenadas ({x} ↔ {ξ}) en el espacio de Minkowski M=\mathbbR1,3 dotado de una métrica ημν con asignatura (1,−1,−1,−1):
ξμ=ξμ(x,s) .(1)
Derivándola sucesivamente respecto del parámetro s, se obtiene
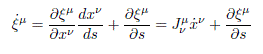
y
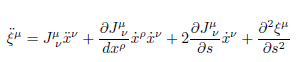
con la matriz jacobiana definida según
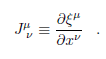
Supongamos que el sistema {x} es inercial mientras {ξ} (no inercial) sigue a la partícula en su movimiento, de modo que ·· ξμ=0, y se contrae entonces con el jacobiano inverso ―J para hacer uso de ―J ρμJ νρ=δ νμ; el resultado es una definición puramente funcional de las aceleraciones:
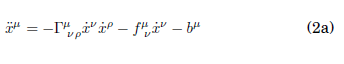
donde
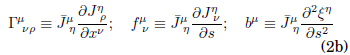
_ ^
La ecuación (2) implica la existencia, en principio, de fuerzas tensoriales (Γ νρμ · xν · xρ), vectoriales ( νμ· xν) y escalares (bμ) en las velocidades. Si, eventualmente, se tiene Γ νρμ· xν· xρ=0 y bμ=0, el remanente de (2a) es
![]()
y sugiere -formalmente- la ocurrencia de fuerzas del tipo electromagnético (si fuera posible reemplazarla con una expresión físicamente tensorial y proporcional a las tetra velocidades).
2 formalismo lagrangiano
En efecto, para el caso que aquà interesa, existe una lagrangiana invariante bajo recalibración (homogénea de primer orden en las velocidades) que es, obviamente, la de la partícula libre ([41982Peñaiel N. & Raanelli]) con acoplamiento electromagnético
![]()
siendo τ una constante caracterÃstica de la partícula y Aμ el tetrapotencial electromagnético. Para L con el tratamiento usual, siendo L(α· x)=αL(· x), se llega a
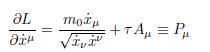
que es la definición del momento canónico (ahora diferente del momento lineal pμ); además,
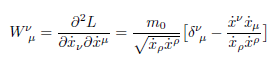
y permite escribir las ecuaciones de movimiento en la forma tensorial:
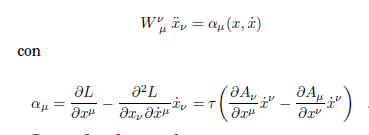
Se verifica de inmediato que W μν· xμ=0, esto es, que la tetravelocidad constituye un autovector nulo de la hessiana, confirmando su singularidad. Ahora, puesto que
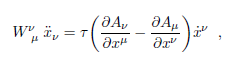
la restricción canónica debiera provenir de αμ · xμ=0, pero la expresión se anula idénticamente
![]()
esto implica que no hay restricción canónica y, consecuentemente a la invariancia de calibre, es posible introducir una restricción auxiliar (subsidiaria) que, para este caso, coincide formalmente con la restricción primaria porque corresponde a la elección de la longitud de línea mundo como parámetro independiente:
![]()
Por tanto, la ecuación de movimiento altante como consecuencia de la singularidad de la hessiana (de rango 3) es,
![]()
la cual conduce a la reducción
![]()
esto es, W actúa ahora como un verdadero proyector (en el espacio de las tetra aceleraciones); entonces, las ecuaciones de movimiento devienen
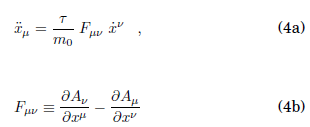
y Fμν coincide, desde luego, con la definición tetradimensional del tensor de Maxwell.
3 formalismo hamiltoniano
Es fácil comprobar que la expresión pμ· xμ − L, para la lagrangiana propuesta (3), se anula idénticamente (el hamiltoniano ordinario no existe). Consecuentemente, el formalismo hamiltoniano para este caso es, como en el de la partícula libre, resultado de una restricción primaria (el método de Dirac requiere que la función hamiltoniana sea una combinaciéón lineal de las restricciones primarias); entonces, usando la que proviene de la definición del momento pμ,
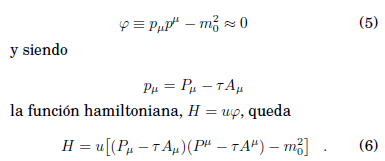
Efectuando los corchetes usuales de las variables canónicas con el hamiltoniano, las ecuaciones de movimiento resultan
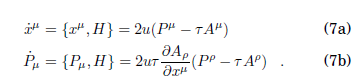
Ahora, el requisito de estabilidad de la restricción se satisface idénticamente debido a que la derivación respecto del parámetro independiente se obtiene mediante el corchete de Poisson de ella con el hamiltoniano, esto es:
![]()
El coeficiente u debe ser determinado mediante la elección del calibre; puesto que se está en libertad de elegir la retricción auxiliar que lo determinará, una posibilidad muy general sería ∫pμdxμ−us ≈ 0, pero ésta no es manejable; como en el caso lagrangiano, sin embargo, la opción inmediata
![]()
significa, por supuesto, que es el arco, s, el que ungirá como parámetro dinámico independiente. Sustituyendo · xμ de (4a), se obtiene
![]()
De ahÃ, como pμpμ ≈ m02, se puede tomar u = 1/2 m0 y escribir ahora la restricción auxiliar en la forma γ ≡ p2−m02 ≈ 0, formalmente igual a φ, por lo cual la estabilidad se satisface de inmediato. Nótese que φ y γ no son idénticas, sin embargo, porque φ es cierta aun si · xμ· xμ ≠ 1 . En adelante, las igualdades "débiles" ( ≈ ) pueden ser sustituidas por igualdades "fuertes" (=) y
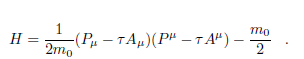
Las ecuaciones (canónicas) de movimiento son, finalmente,
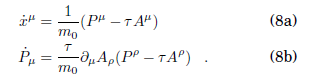
4 Conclusiones
Las ecuaciones de movimiento (8) son, por supuesto, las mismas que (4), lo cual se comprueba fácilmente derivando (8a) y usando (8b) para eliminar · Pμ. La fuerza de Minkowski
![]()
queda, así, expresada en términos del tensor de Maxwell el cual, por supuesto, es el mismo que aparece en las leyes de Maxwell manifiestamente covariantes para el campo electromagnético. Otros enfoques, que desembocan en las mismas ecuaciones de movimiento, prefieren tratar con lagrangianas regulares, sacrificando la invariancia de calibre ([32007Lemos]).
Conflicto de intereses Los autores declaran que no hay conflicto de intereses con respecto a la publicación de éste documento.
References
Dirac, P. 1964, Lectures on Quantum Mechanics (Yeshiva University) [ Links ]
Jackson, J. 1998, Classical Electrodynamics Third Edition 3rd Edition (Wiley) [ Links ]
Lemos, N. A. 2007, Mecânica Analótica - 2A. ED. (Livraria da isica) [ Links ]
Peñaiel N., V. M. & Raanelli, K. 1982, Il Nuovo Cimento B (1971-1996), 72, 157 [ Links ]
Sudarshan, E. & Mukunda, N. 1974, Classical Dynamics: A Modern Perspective (Wiley) [ Links ]














