Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista Boliviana de Física
On-line version ISSN 1562-3823
Revista Boliviana de Física vol.35 no.35 La Paz Dec. 2019
B. CONTRIBUCIONES Y REVISIONES
Del movimiento browniano a los motores brownianos
From brownian motion to brownian motors
L. A. Manzaneda Osorio G.†
† Carrera de Física, Universidad Mayor de San Andres c. 27 Cota-Cota, Campus Universitario
Casilla de Correos 8635 La Paz - Bolivia
lmanzaneda@fiumsa.edu.bo
Resumen
En el presente trabajo se estudia el fenomeno de obtener movimiento en una dirección pref-erencial a partir del movimiento aleatorio de partículas microscopicas como una consecuencia de sistemas con potencial asimetrico y periódico espacialmente. En adición, se explora brevemente el fenomeno de transporte de la kinesina en microtúbulos.
Codigo(s) PACS: 83.10.Mj - 02.30.Em - 87.16.Nn
Descriptores: Movimiento browniano - teoría de los potenciales - kinesina.
Abstract
In this paper we study the movement in a preferential direction obtained from the random movement of microscopic particles as a consequence of systems with spatial asymmetric and periodic potential. In addition, the transport phenomenon of kinesin in microtubules is briefly explored.
Subject headings: Brownian dynamics Potential theory — Kinesin.
1. INTRODUCCION
El movimiento browniano hace referencia al movimiento de partículas microscopicas que experimentan un movimiento aleatorio debido a fluctuaciones termicas, fenómeno observado por primera vez en 1827 por R. Brown y descrito formalmente en 1905 por A. Einstein. En 1963 R. Feynman propone un dispositivo que realiza trabajo a partir del movimiento aleatorio, (Feynman et al. 1963). En base a este mecanismo se discuten nuevos sistemas microscopicos fuera del quilibrio térmico que consiguen un movimiento dirigido por medio de potenciales tipo ratchet, (Astumian 1997). Los motores brownianos surgen como una consecuencia de obtener movimiento en una direccion a partir del movimiento browniano a escala microscopica, principal diferencia con un motor termico convencional.
En la siguiente seccion se discute el funcionamiento de un motor browniano propuesto por R. Feynman, como punto de partida para sistemas con potenciales asimetricos (tipo ratchet), cuyo formalismo se revisa brevemente en la seccion 3, posteriormente en la seccion 4 se discute acerca del movimiento de particulas brownianas en potenciales flashing ratchet y rocking ratchet. En la seccion 5 se analiza el transporte de la kinesina sobre microtubulos que pueden ser modelados por potenciales tipo ratchet como aplicacion a sistemas biológicos y por ultimo, en la seccion 6, se presentan las conclusiones y recomendaciones bibliograficas en caso de querer profundizar sobre el tema.
2. RUEDA DENTADA Y TRINQUETE DE FEYNMAN
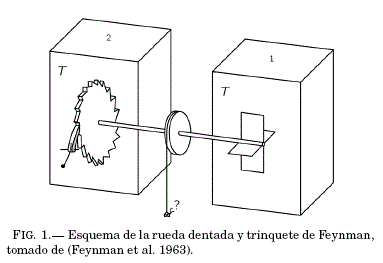
La rueda dentada y trinquete es un dispositivo ingenioso ideado por R. Feynman (Feynman et al. 1963), que a primera vista pretende violar la segunda ley de la termodinamica la cual según la declaracion de Kelvin-Planck afirma que; en ningún proceso cíclico es posible la extracción de energía de un reservorio de calor, y la conversión de toda esa energía en trabajo. Este dispositivo en escala mesoscopica consta de dos cajas que contienen cierto gas a la misma temperatura T, en un caja hay un eje con aspas que conecta con la otra caja donde esta la rueda dentada y el trinquete (o gatillo), ver Fig. 1. Debido al movimiento browniano de las partículas en la caja 1, las multiples colisiones con las aspas transmitiran un movimiento de rotación a la segunda caja, no obstante este movimiento es sesgado a una direccion de giro favorable debido al sistema de rueda dentada y trinquete. Incluso, segun Feynman podría atarse a una "pulga" para levantarla, como se muestra en la Fig. 1. En otro sentido este dispositivo consigue un tipo de movimiento perpetuo lo cual va en contra de la segunda ley de la termodinamica, i.e.se extrae el calor de los reservorios (cajas a temperatura constante) y se convierte completamente en trabajo (levantando la pulga) en un proceso ciclico.
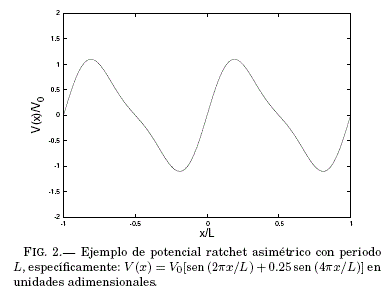
Es evidente que este dispositivo no puede funcionar ya que en la naturaleza no existe un movimiento aislado perpetuo y una de las razones se debe a que la rueda dentada y el trinquete tambien tienen movimiento Browniano, esto provoca que el trinquete ocasionalmente se levante justo cuando el movimiento de las aspas se da en sentido contrario y cuanto mas se eleva la temperatura de estas cajas, esto ocurre con mayor frecuencia, por lo que el movimiento neto es nulo. Por otro lado si la temperatura en la caja 1 es mayor a la temperatura donde se encuentra la rueda dentada y el trinquete (T1> T2), la colision de las partículas con las aspas sera mucho mas frecuente que el movimiento browniano del trinquete, con lo cual se consigue que el dispositivo rote en un sentido favorable, esto no va en contra de la segunda ley de la termodinamica debido a que la transferencia de energía ocurre de un reservorio de mayor temperatura T1 a un reservorio de menor temperatura T2. Este mecanismo de movimiento circular puede ser adaptado a un movimiento lineal a traves de un potencial asimetrico de diente de cierra, conocido comunmente como potencial ratchet, Fig. 2.
Este tipo de potencial simula una perturbacion externa que da lugar al transporte de particulas en una direccion, lo que se conoce como efecto ratchet.
Por otro lado en caso de anadir una fuerza externa que se opone a este movimiento (e.g., levantamiento de peso) y a pesar de ello el transporte continua, significa que el sistema realiza trabajo sobre esta fuerza. Debido a ello tales sistemas son llamados motores brownianos.
3. FORMALISMO
Una particula suficientemente pequeña inmersa en un fluido, debido a fluctuaciones termicas exhibe movimiento browniano, cuya evolucion en el tiempo puede ser descrita por la ecuacion de Langevin (un tipo de ecuacion diferencial estocástica), para ello se considera una partícula de masa m en una dimension con coordenada x(t) sujeta a un potencial asimetrico periódico V(x)= V(x + L) (potencial ratchet), ademas de efectos térmicos con el ambiente tales como disipacion de energía y ruido térmico (Reimann & Hanggi 2002), entonces la dinámica de la partícula esta dada por:
![]()
La fuerza de friccion que experimenta la partícula con su ambiente es descrita por ![]() , donde γ es el coeficiente de friccion, mientras que las fluctuaciones termicas
, donde γ es el coeficiente de friccion, mientras que las fluctuaciones termicas ![]() quedan descritas por el ruido blanco Gaussiano de media cero
quedan descritas por el ruido blanco Gaussiano de media cero ![]() = 0 y relacion de fluctuación-disipación dada por:
= 0 y relacion de fluctuación-disipación dada por:
![]()
donde kB es la constante de Boltzmann, T es la temperatura del medio, δ(t) es la funcion delta-Dirac, el término 2γkBT representa la intensidad del ruido.
Por otro lado al tratarse de una partícula browniana y con la constancia de experimentos el factor m/γ es del orden de pico-segundos (Julicher et al. 1997), por lo que como una muy buena aproximacion se desprecia el termino inercial ![]() dando lugar a la ecuacion de Langevin:
dando lugar a la ecuacion de Langevin:
![]()
A partir de esta ecuacion se puede construir la correspondiente ecuacion de Fokker-Planck (Reimann 2002) para la evolucion temporal de la densidad de probabilidad, la cual esta dada por:
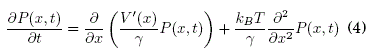
Los terminos primero y segundo del lado derecho de la ecuacion (4) son conocidos como "drift term" (termino de arrastre o deriva) y "difussion term" (termino de difusión) respectivamente. Esta ecuación puede ser expresada en terminos de una densidad de corriente de probabilidad:
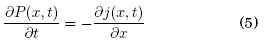
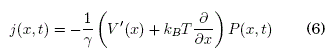
Ahora bien, si se considera una fuerza estatica adicional F que modela el efecto de un torque constante como en el dispositivo de la Fig. 1, lo cual corresponde a una generalizacion de la ecuación (3), la ecuación de Langevin toma la forma:
![]()
Es posible englobar el potencial ratchet V(x) y la fuerza F dentro de un potencial efectivo, de la forma:
![]()
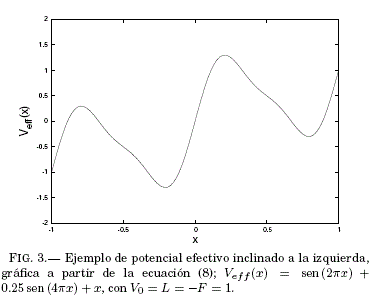
Dependiendo de si la fuerza F es negativa o positiva, las partículas sujetas al potencial efectivo se moveran en promedio pendiente abajo a la izquierda o derecha respectivamente, como se muestra en Fig. 3.
4. POTENCIALES RATCHET
4.1. Flashing ratchet
Este tipo de potencial ademas de ser tipo ratchet, periodico y asimétrico, se caracteriza por ser intermitente entre los estados prendido (on) y apagado (off). El modelo es descrito por la ecuacion de Langevin:
![]()
Donde f(t) representa una funcion de control que le da el caracter intermitente al potencial y es restringida a los valores ±1. Cuando f(t) toma el valor de -1 cancela la accion de V(x), que se interpreta como un estado off del potencial, mientras que si f(t) = 1 el potencial V(x) esta activo, es decir, en estado on. Esta ecuacion modela la dinámica de las partículas sometidas a este tipo de potencial, ahora bien si se considera la interaccion con una fuerza F externa, la ecuacion (9) toma la siguiente forma:
![]()
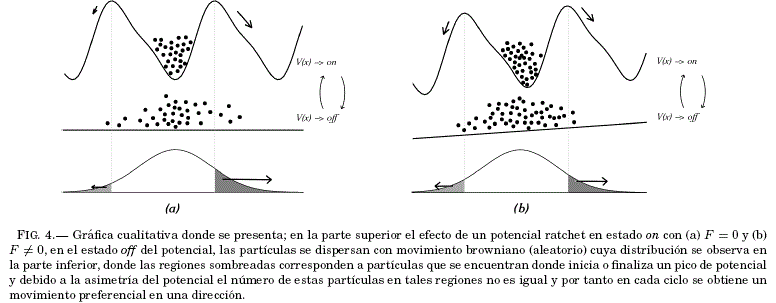
El comportamiento de estas particulas sujetas a este tipo de potencial flashing ratchet se visualiza en la Fig. 4.(a) y en la Fig. 4.(b) se considera la interaccion con una fuerza externa no nula F ≠ 0.
La energia térmica (kBT) de las partículas es menor a la altura del potencial V(x), es decir, cuando el potencial se encuentra en estado on las partículas quedan concentradas en los puntos mínimos del potencial y cuando el potencial es desactivado (estado off) las partículas son libres de difundirse con movimiento browniano, como se muestra en la Fig.4. El ciclo de apagado y encendido (off-on) del potencial induce un movimiento de partículas en una direccion particular debido a la asimetría del potencial obteniendo un flujo neto de partículas ⟨x⟩ ≠ 0. Para lograr tal proposito el periodo de tiempo para el potencial en estado on-off no debe ser muy corto, ya que si lo fuera, las partículas no tendrían tiempo suficiente para difundirse y practicamente se quedarían atrapadas en cercanías del mínimo de potencial y por tanto el flujo neto de particulas seria nulo ![]() = 0.
= 0.
En presencia de una fuerza externa F, el movimiento de las partículas en sentido opuesto al de esta fuerza es posible, si la misma no es muy intensa, como se observa en la Fig. 4.(b), en tal caso el sistema realiza trabajo, accion de un motor browniano. Por otro lado si la fuerza externa es muy grande, el flujo de la partículas debido al potencial flashing no es posible y el movimiento neto de las partículas es causado por este agente externo, lo cual no corresponde a un motor browniano ya que se realiza trabajo sobre el sistema.
4.2. Rocking ratchet
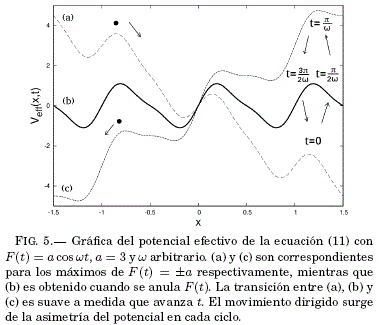
Este tipo de potencial, a diferencia del estudiado en la subseccion previa, consiste de una fuerza periódica en el tiempo. La ecuacion de Langevin que modela este caso es similar a la ecuacion (7) con la diferencia de que la fuerza aplicada es dependiente del tiempo F(t) y analogamente a la ecuación (8) el potencial efectivo es de la forma:
![]()
Este potencial se regira entre dos limites marcados por los máximos ±|F(t)| de la fuerza aplicada, esto y la dinamica del sistema se observa en la Fig. 5. El movimiento dirigido se consigue en cada ciclo de F(t) y con la asimetría del potencial V(x).
5. APLICACIONES A MOTORES MOLECULARES
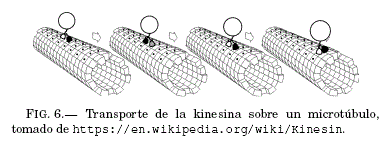
A escala microscopica en células eucariotas se encuentran cierto tipo de proteínas motoras como la kinesina que se transporta sobre los microtúbulos (estructuras celulares formadas por polimeros proteicos) a partir de la energia liberada por la hidrólisis de ATP (nucleotido fundamental en la obtención de energía celular), cuya reaccion es dada por la ecuacion (12) y el proceso se muestra en la Fig. 6. El movimiento constante de la kinesina es compatible con funciones celulares muy importantes como ser la mitosis, meiosis y transporte axonal.
![]()
donde Pi corresponde a un grupo de fosfato inorganico.
El mecanismo de conversion de energía recolectada de la hidrolisis de ATP en un progresivo movimiento sobre los microtubulos por la kinesina puede ser estudiado desde el formalismo de los motores browni-anos con potencial ratchet, (Xie 2010), por ejemplo, se considera el potencial flashing ratchet como modelo para describir la dinamica de la kinesina, donde las particulas brownianas son reemplazadas por ésta proteína. El potencial en estado on corresponde a la kinesina en estado ATP y cuando el potencial se anula la kinesina se encuentra en estado ADP. La aplicacion cíclica de (12) genera un movimiento favorable hacia la dirección positiva del microtubulo.
El comportamiento de una partícula browniana dentro del potencial intermitente es analogo al comportamiento de la kinesina en un ciclo dado por la ecuacion (12), debido a ello, el modelo de motores brownianos con potencial flashing ratchet es investigado para describir la dinamica de esta proteína, incluso es posible modelar la accion de una fuerza externa que apunta a la dirección negativa del microtubulo, de manera similar a la ec. (8), (Xie 2010).
6. CONCLUSIONES Y RECOMENDACIONES
Este trabajo describe de manera resumida el mecanismo de generar movimiento en una direccion preferencial a partir del movimiento browniano de partículas a escala microscopica con la imple-mentacion de potenciales tipo ratchet y por tanto este trabajo puede servir como punto de partida para un estudio mas detallado acerca de los motores brownianos, (Reimann 2002).
Se recomienda al lector, en caso de profundizar mas acerca de motores moleculares, consultar; (Julicher et al. 1997), donde se estudian sistemas biologicos a pequeña escala que convierten energía química en mecanica, comportamiento típico de un motor molecular, tambien se puede consultar, (Tu & Cao 2018), donde se estudia el rendimiento de un motor molecular con un analisis analítico y numerico.
Conflicto de intereses Los autores declaran que no hay conflicto de intereses con respecto a la publicacion de éste documento.
REFERENCIAS
Astumian, R. D. 1997, Science, 276, 917 [ Links ]
Avellaneda, D. R. & Naranjo, R 2014, Ciencia en Desarrollo, 5, 173 [ Links ]
Feynman, R., Leighton, R., & Sands, M. 1963, The Feynman Lectures on Physics, Volume 1 (Addison-Wesley) [ Links ]
Julicher, F., Ajdari, A., & Prost, J. 1997, Rev. Mod. Phys., 69, 1269 [ Links ]
Parrondo, J. M. & de Cisneros, B. 2002, Applied Physics A, 75, 179 [ Links ]
Reif, R 1965, Fundamentals of statistical and thermal physics (McGraw-Hill Book Company) [ Links ]
Reimann, P. 2002, Phys. Rep., 361, 57 Reimann, P. & Hanggi, P. 2002, Applied Physics A, 75, 169 [ Links ]
Tu, Y. & Cao, Y. 2018, Phys. Rev. E, 97, 022403 [ Links ]
Xie, P. 2010, International journal of biological sciences, 6, 665 [ Links ]