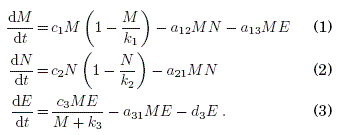Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista Boliviana de Física
On-line version ISSN 1562-3823
Revista Boliviana de Física vol.35 no.35 La Paz Dec. 2019
A. ARTÍCULOS
Análisis de la dinámica poblacional de células canserosas,
mediante un modelo de Radiosensibilidad
Analysis of the dynamics of cancerous cell populations using
a Radiosensivity model
Winder A. Canezo-Gómez1, Gloria Rodrigo2, & Gonzalo Marcelo Ramírez-Ávila3
1Carrera de Biología, Universidad Mayor de San Andres.
2Instituto de Biología Molecular y Biotecnología, Universidad Mayor de San Andres.
3Instituto de Investigaciones Físicas, Universidad Mayor de San Andres.
Campus Universitario, c. 27 Cota-Cota. La Paz - Bolivia
Recibido: 5 de septiembre de 2019 aceptado: 27 de noviembre de 2019
Resumen
Este trabajo describe la dinamica poblacional de células cancerosas en interacción con celulas normales, así como con células efectoras que están relacionadas con la respuesta inmunologica. El modelo se basa en ecuaciones logísticas que describen el crecimiento de las poblaciones de celulas cancerosas y normales, en las ecuaciones de Lotka Volterra para especies en competencia, incluyendo los efectos de la radiacion en ambos tipos de células; finalmente, se utiliza la ecuacion de Michaelis-Menten que da cuenta de la interacción entre celulas cancerosas y efectoras. Los parámetros del modelo están en relación con las interacciones entre los diferentes tipos de celulas y en particular, sobre los efectos de inactivación de celulas cancerosas debido a la acción de las normales, además de la transformación de celulas normales causada por la presencia de las tumorales. En el presente trabajo tambien consideramos la radiosensibilidad de cada tipo de celulas. Realizamos un análisis de estabilidad lineal del modelo, determinando proyecciones en tres dimensiones de hiper volumenes de estabilidad en el espacio de parametros. El modelo exhibe una gran riqueza dinamice que va desde puntos fijos a comportamientos caoticos. Consideramos varias regiones del espacio de parametros buscando situaciones que conduzcan a la eliminación de células tumorales por efecto de la radiacion, sin modificar o disminuyendo ligeramente la población de células normales. Esta ultima situación podría constituir una aplicacion importante del trabajo, relacionado con un tratamiento eficaz de la radioterapia en pacientes con cancer.
Codigo(s) PACS: 87.19.xj - 87.55.Qr - 05.45.Ac
Descriptores: Cancer - radioterapia - caos de pocas dimensiones.
Abstract
This work describes the population dynamics of cancerous cells when they interact with healthy cells, as well as, effector cells that defend the body in an immune response. The model is based on logistic equations that describe the growth cancerous and healthy cell population. The Lotka-Volterra equation for competitive species includes the radiation effects on both cells and the Michaelis-Menten equation considers the interaction between cancerous and effector cells. The parameters of the model are related to the interactions between the different types of cells. It is crucial to take into account the inactivation of the cancerous cells produced by the action of the other types of cells. On the other hand, it is also essential to consider the transformation of the healthy cells caused by the presence of tumor cells. We also discuss the radiosensitivity of each type of cell. We performed the linear stability analysis of our model, determining stability volumes in several projections of the hypervolume of the parameter space. The model exhibits a great dynamical richness going from fixed points to chaotic behaviors. We took into consideration several regions of the parameter space looking for parameter values leading to the situation in which the radiation tends to eliminate the tumor cells with no or slight modifications on the healthy cells populations. The latter could constitute an essential application for effective radiotherapy treatment.
Subject headings: Cancer - radiotherapy low-dimensional chaos.
1. INTRODUCCION
El cancer refleja alteraciones genéticas de una celula, cuyo crecimiento es diferente a las células vecinas, donde las celulas cancerosas se multiplican de manera descontrolada como lo senala Menchón (2007), entre otros. El sistema inmunologico, al detectar la proliferacion descontrolada de las células cancerosas, segrega sustancias toxicas para eliminarlas; sin embargo, algunas celulas del sistema inmunologico mueren en este proceso tal como lo apunta Galach (2003). Así, estas celulas son reemplazadas por otro lote de celulas efectoras, que repiten el proceso de manera cíclica como lo mencionan Valle et al. (2014). Por otro lado, las celulas normales interactuan con las células cancerosas y su presencia permite que se inhiban mutuamente, aspecto indicado por de Pillis & Radunskaya (2003) y Kuznetsov et al. (1994).
En este caso, es mas probable que las células normales imiten la capacidad de multiplicacion de las celulas cancerosas por lo que las células normales vecinas se transforman en cancerosas, como lo establece Menchon (2007). Román (2007) afirma que los diferentes tipos de cancer, en general son atacados por una combinacion de tratamientos como la radioterapia y la quimioterapia. Segun Rizo-Potau (2016), la radioterapia afecta el sistema de repli-cacion de las células malignas y según Pinar-Sedeño et al. (2004) es utilizada para combatir linfomas y canceres sólidos, mientras que la quimioterapia utiliza farmacos para eliminar las células cancerosas como lo mencionan Menchon (2007), enfocándose al tratamiento de leucemias y mielomas, segun afirman Gómez-Almaguer et al. (2010). Por otro lado, segun Román (2007), los procedimientos quirúrgicos tienen por objeto extraer las celulas tumorales.
La radiacion actúa de modo que, a mayor dosis, una cantidad mas elevada de células cancerosas es atacada. Este tratamiento puede generar complicaciones cuando se irradia una proporcion significativa de celulas sanas como lo indican Calvo & Escude (1985) y Belostotski & Freedman (2005), quienes concluyen que se debe hacer un analisis costo-beneficio en estos casos.
Liu & Yang (2014) presentan un modelo matematico concerniente al tratamiento del cáncer con radioterapia, en el que se analiza la coexistencia de celulas sanas y cancerosas. Por otra parte, Isea & Lonngren (2015), tambien estudian un modelo competitivo en el cual se considera la accion de la radiacion en el sistema. Asimismo, Itik & Banks (2010) utilizan un modelo dinamico de expansión del cancer, que incluyen a células de tejido sano, canceroso y celulas del sistema inmunitario, que conlleva a un comportamiento estrictamente caotico. Por otro lado, Gallas et al. (2014) estudian el modelo de crecimiento de cancer planteado por de Pillis & Radunskaya (2003), clasificando los estados oscilatorios que presenta fases de regularidad y caos.
Por ultimo, se puede mencionar a Ghaffari et al. (2016), que utilizan un sistema de ecuaciones diferenciales para describir la accion de la radioterapia y quimioterapia, examinando la interaccion entre celulas del sistema inmunológico, cancerosas y el agente quimioterapeutico que juega el rol de depredador, sus resultados proponen que el tratamiento deberıa cambiar la dinámica del cáncer y no solo reducir la poblacion de células cancerosas optimizando el tratamiento tradicional. Existen otros tratamientos como la la inmunoterapia y las combinaciones de los diversos tratamientos como lo especifican Castorina et al. (2007). Por ejemplo, si la cirugía extirpa el cumulo de células cancerosas, puede optimizarse sus resultados eliminando su propagacion a células sanas utilizando la radioterapia para controlar el crecimiento de las celulas cancerosas que quedaron en el sistema del individuo, aspectos estos mencionados por Castorina etal. (2007).
Luego, para el analisis de este artículo se pretende, describir el comportamiento poblacional de celulas cancerosas irradiadas, mediante una simulacion computacional, de acuerdo a las radiosensibi-lidades de los organos afectados. En ese sentido, el trabajo se estructura de la siguiente manera: en la Sec. 2, se explica el estado del arte del problema y los modelos a ser utilizados para el analisis. Las cuencas de atraccion obtenidas utilizando el modelo más general se muestran en la Sec. 3, donde tambien se ilustran series temporales correspondientes a situaciones interesantes provenientes de la inspeccion de las diferentes cuencas de atraccion. Finalmente, en la Sec. 4 se resaltan los resultados mas importantes del trabajo y sus implicaciones, así como las perspectivas que se traduciran en la continuación de la investigacion teniendo como meta el acercarnos a situaciones mas realistas que conduzcan a mejoras en los tratamientos de radioterapia.
2. MÉTODOS
Los modelos que involucran la accion de la radiacion sobre conjuntos de células cancerosas y normales deben considerar que el parametro relacionado con la radiacion esté íntimamente ligado con la dosis absorbida y/o con la equivalente, Las ideas iniciales del presente trabajo surgen de los resultados obtenidos por Ramírez-Ávila (2017) donde se plantea el modelo poblacional de celulas cancerosas, normales y efectoras con base en ideas típicas utilizadas en este tipo de modelos, tales como las ecuaciones logıstica, de Lotka-Volterra y de Michaelis-Menten, ademas de introducir un parámetro relacionado con la radiacion que afecta, en su forma general, tanto a las celulas cancerosas como a las vecinas normales. Para poner en contexto el significado de las ecuaciones y los parametros presentes en las mismas, se describen a continuacion los modelos sin y con el termino correspondiente a la radiación.
2.1. Modelo sin radiación
Se plantea un modelo de competicion de Lotka-Volterra, que permite encontrar un mecanismo de interaccion entre dos especies diferentes; en este caso, se tendra las células malignas o cancerosas M(t), las celulas sanas o normales N(t) y las celulas efectoras o pertenecientes al sistema inmunologico E(t). Ini-cialmente se utilizara el modelo normalizado de Itik & Banks (2010), que presenta la siguiente estructura:
El primer termino de la Ec. (1) está relacionado con el crecimiento logístico de las celulas cancerosas en ausencia de otras poblaciones celulares. En este caso, la capacidad de carga es k1 y la tasa de crecimiento es c1. La competicion entre las células sanas N(t) y las cancerosas M(t), disminuye la tasa de crecimiento de estas ultimas. Finalmente, la eliminación de células cancerosas, debida a la accion de las células del sistema inmunologico E(t) es descrita por el termino caracterizado por α13.
La Ec. (2) describe la tasa de crecimiento de poblacion de células sanas o normales, donde el primer termino está relacionado con el crecimiento logístico, con una capacidad de carga k2 y tasa de crecimiento c2. Se asume que la proliferacion de celulas cancerosas es más rápida que la correspondiente a las celulas sanas, de modo que c1 > c2. Ademas, las células cancerosas inactivan a las celulas sanas a una tasa α21.
La Ec. (3) da cuenta de la tasa de variacion de las celulas del sistema inmunológico o células efectoras. El primer termino describe la estimulación de las celulas cancerosas sobre el sistema inmunológico, en tanto que el segundo esta relacionado con la inactivacion de las células del sistema inmunológico por accion de las células cancerosas a una tasa α31. Por ultimo, las células del sistema inmunológico pueden desaparecer de manera natural a una tasa dE.
Desde el punto de vista biologico existe una variedad de celulas del sistema inmunológico que se activan ante la presencia de diversos agentes que pretenden afectar a un organismo, si bien su presencia y actividad biologica son diferentes, acá se se las considera como si fuesen de un solo tipo, cuya accion es unicamente inactivar las células cancerosas y evitar su proliferacion. Por otro lado, se espera que en una situacion hipotética en la que las células cancerosas hubiesen sido eliminadas, las celulas del sistema inmunologico dejarían de actuar en el organismo.
El modelo propuesto considera a las celulas del sistema inmunologico como linfocitos T citotóxicos (CTL), las Natural Killer NK y se producen como celulas vírgenes que no muestran respuesta alguna a las celulas cancerosas; a menos que, se activen por las celulas portadoras de antígenos (APC) a través de proteínas especializadas llamadas moleculas del complejo principal de histocompatibilidad (MHC) en presencia de antígenos específicos de tumor, como lo mencionan Abbas et al. (2015).
Por simplicidad consideraremos el modelo original obtenido por de Pillis & Radunskaya (2003) que implica un reajuste y adimensionalizacion del sistema de ecuaciones:
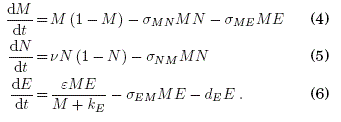
Es importante hacer notar que los factores σ, responden a la siguiente interpretación: σxy = tasa de inactivacion de las células x, debidas a las células y. En nuestro caso, σMN esta en relación a la inactivación de las celulas cancerosas debido a la presencia de las normales; mientras queσNMesta relacionada a la transformacion de las células normales en malignas.
2.2. Modelo con radiación
La radioterapia tiene su origen en el concepto de que las celulas tumorales son más sensibles a la radiacion que las normales Bergonié & Tribondeau (1906) y complementada con otras investigaciones como las de Wintz (1938). Así, cuando se quiere emplear un modelo que sea util en radioterapia, se debe considerar la aplicacion de cierta dosis de radiación sobre el sistema, por lo que toma la forma:
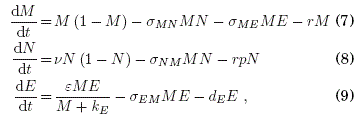
donde el factor p, esta en relación con la radiosensi-bilidad normalizada de las celulas sanas comparada a aquella de las cancerosas 0 < p ≤ 1; en tanto que el coeficiente r, esta ligado con la intensidad de radiacion recibida por el sistema y por ende con la dosis. Es importante senalar que los parámetros r y p son experimentalmente estimables mediante la determinacion de la dosis equivalente (H). Como ya se menciono anteriormente, las características dinamicas de las células del sistema inmunológico juegan un papel importante para la lucha contra los agentes externos que pudiesen afectar a las celulas normales, tal como lo senalan de Pillis & Raduns-kaya (2003).
El analisis del modelo con radiación está sujeto a los coeficientes de las ecuaciones diferenciales que permiten la construccion del espacio de parametros y sus correspondientes proyecciones que permiten establecer la dinamica del sistema. Los valores apropiados a ser utilizados como valores de los parametros fueron obtenidos a través de un análisis de estabilidad del modelo, mismo que fue obtenido por Ramírez-Ávila (2017), donde además se muestran las diferencias entre los modelos con y sin radiación.
Otra forma de estudiar sistemas dinamicos es a traves de las denominadas cuencas de atracción que se las define como conjuntos de condiciones iniciales que conducen a un determinado atractor como lo senala Ott (1993) o en situaciones a multiesta-bilidad, situacion referida por Pisarchik & Feudel (2014); es decir, a posibles estados finales diferentes que dependen de las condiciones iniciales. Nos valdremos de esta tecnica para explorar condiciones iniciales que conduzcan a situaciones en las que la aplicacion de la radiación tenga como resultado la eliminacion de las células cancerosas (ver Sec. 3.1). Es así que a partir de las cuencas de atraccion obtenidas, se hace un analisis del comportamiento de las poblaciones celulares, variando los parametros, dentro de las regiones de estabilidad, que permitira hacer algunas interpretaciones biologicas, referentes al comportamiento de las celulas cancerosas y las células normales. Por consiguiente, se describira el comportamiento poblacional de celulas cancerosas irradiadas, así como los efectos que pueden darse en celulas vecinas normales, para encontrar la solución optima, que maximice el efecto nocivo de la radiación sobre las celulas cancerosas, y minimice su efecto sobre las celulas normales.
3. RESULTADOS
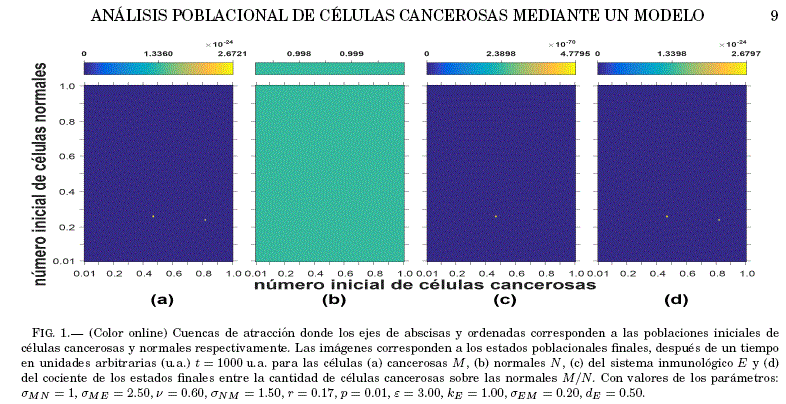
El analisis de estabilidad realizado por Ramírez-Avila (2017), permitió determinar las regiones de estabilidad para situaciones en las que se tiene radiacion actuando sobre células cancerosas y normales, considerando ademas que cada uno de estos tipos de celulas tienen radiosensibilidades diferentes. En este caso, cuando la radiacion actúa sobre el sistema (celulas cancerosas y normales), se obtuvieron cuencas de atraccion bajo diferentes criterios: poblaciones finales de celulas después de un tiempo t (a) cancerosas M, (b) normales N, (c) efectoras E y (d) razon de células cancerosas a normales M/N, como las que se muestran en la Fig. 1.
Obsérvese que la distribución de valores iniciales para las celulas cancerosas y normales van de cero a uno, mientras que la población inicial correspondiente a las celulas del sistema inmunológico es de 0.01 y se activa con la presencia de las celulas cancerosas en el organismo.
Segun las gráficas mostradas, los estados finales encontrados en todos los tipos de celulas están representados por un color determinado de una barra de colores con la escala correspondiente. En el caso particular de la Fig. 1 donde la desaparicion de algun tipo de célula es reflejada con el color extremo de valor inferior en la barra de colores (Figs. 1(a), (c) y (d)). El hecho anterior se refleja tambien por la escala de valores extremadamente pequena que muestran para estos casos las barras de colores. En otros terminos, sin importar las poblaciones iniciales de celulas normales y cancerosas, se llega al mismo comportamiento poblacional final. Se hace notar que la resolucion de todas las cuencas de atraccion mostradas en este trabajo es de 100x100 píxeles.
En los graficos posteriores solamente se mostrarán las cuencas de atraccion correspondientes a una de las poblaciones celulares o en su defecto, a la razon de las poblaciones de celulas cancerosas y normales. En todos los casos, se considerara un tiempo de 1000 unidades arbitrarias (u.a.) con un paso maximo de 10-3 utilizando por simplicidad como metodo de integracion el de Runge-Kutta (4,5) al ser una librería de Octave. El tiempo de integracion está en relación con el tiempo de irradiacion, el cual a su vez estará en funcion de la dosis planificada, la cual, dependerá del equipo con el que se este trabajando. En otras palabras, se llegar a la dosis en el tiempo que dure la sesion de radioterapia. Así por ejemplo, si la sesion dura cinco minutos, este tiempo corresponde a las 1000 u.a. mencionadas anteriormente. Los resultados obtenidos analizando las regiones de estabilidad se describen a continuacion.
3.1. Eliminación de células cancerosas
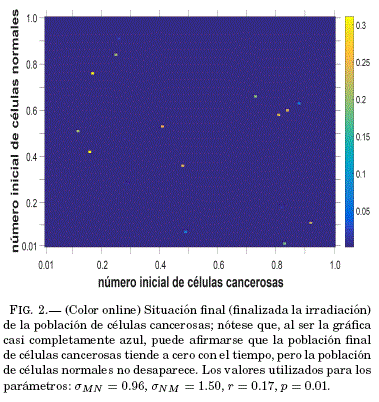
En el entendido que el modelo esta pensado en que puede ser generalizado para su uso en situaciones que impliquen irradiar celulas cancerosas y normales, como ocurre cuando se realiza un tratamiento de radioterapia; el analisis de las cuencas de atraccion estará orientado bajo ese enfoque. Así, se puede observar situaciones en las que es conveniente aplicar radioterapia. Los parametros establecidos dentro de las regiones de estabilidad que conducen a la eliminacion de las células cancerosas y que son considerados fijos para obtener las cuencas de atraccion son: σME = 2.50, & = 0.60, ε = 3.00, kE = 1.00, σEM = 0.20, dE = 0.50; en tanto los que pueden variar son: σMN, σNM, r y p.
De donde la cuenca obtenida esta representada en la Fig. 2; en la cual, se puede ver que no importa la poblacion inicial de las células cancerosas, el paciente puede encontrarse en un estado inicial de cancer o en una fase final, luego del tratamiento, la poblacion final de las células cancerosas es cercana a cero. Sin embargo, la poblacion de células normales sobrevive. Ademas se observa que la población de celulas efectoras al final del proceso también se reduce hasta eliminarse, pues su presencia ya no es necesaria al haber desaparecido las celulas cancerosas. Asimismo, se nota la presencia de puntos de distinto color al azul; esto se debe a que las cuencas de atraccion fueron obtenidas integrando hasta 1000 u.a. de tiempo, siendo que los píxeles representando colores diferentes al azul dan cuenta de condiciones iniciales que conducen a la casi eliminacion de las células cancerosas para tiempos mayores a 1000 u.a. Así por ejemplo, para la condicion inicial (M0,N0) = (0.16,0.42), la casi eliminacion de las celulas cancerosas ocurre luego de 1154 u.a. de tiempo. Para los otros pıxeles de colores, se verifica que las condiciones iniciales asociadas a los mismos, tambien conducen a la casi eliminación de las células cancerosas sin afectar a las celulas normales.
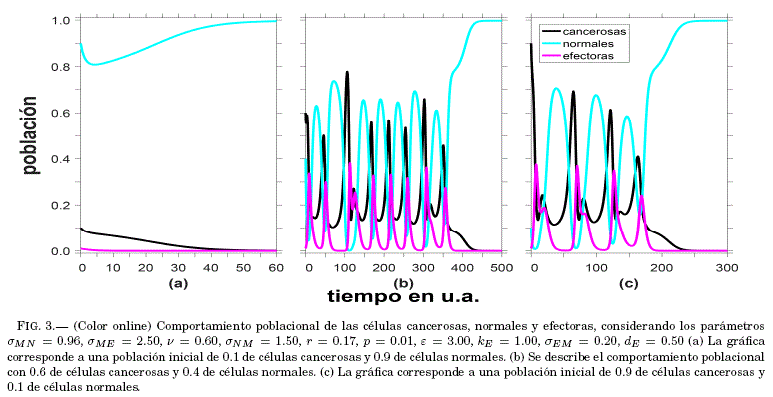
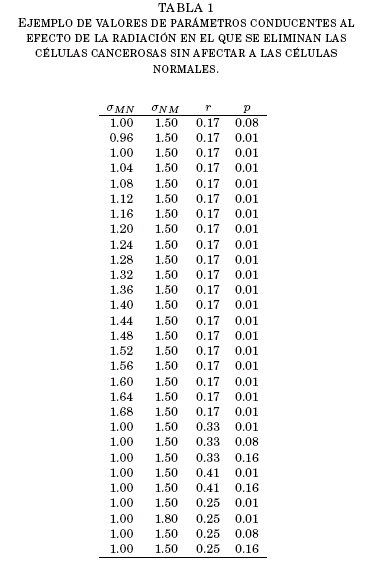
En la Fig. 3 se muestra la grafica correspondiente a las series temporales de los tres tipos de celulas con diferentes poblaciones iniciales. En las mencionadas series de tiempo, se verifica que al margen de las condiciones iniciales de las poblaciones celulares, el tratamiento logra reducir la poblacion de las celulas cancerosas, tendiendo su valor a cero. Lo mismo ocurre con las celulas del sistema in-munologico que se inactivan al eliminarse las células malignas, acompanando el comportamiento de estas; es decir, si las celulas tumorales se eliminan, tambien lo harán las efectoras. Por otro lado, la cantidad de celulas normales tiende a ser predominante, no viendose afectada por la acción de la radiación. En estas series de tiempo, hay una clara tendencia hacia un punto fijo (constancia de las poblaciones), donde los transitorios pueden jugar un rol importante en el sentido de que permitiran la planificación de la irradiacion, de manera tal que se garantice el objetivo de la eliminacion de células cancerosas. Como se menciono anteriormente, existen varias regiones con diversos parametros en las que el comportamiento poblacional de las celulas cancerosas disminuye por efectos de la radiacion, sin afectar a la población de celulas normales, estos pueden resumirse en la Tabla 1. Los valores de los parametros fueron elegidos barriendo toda la gama de valores dentro de las regiones de estabilidad y escogiendo aquellos que conducen a tener como resultado la eliminacion de las celulas cancerosas. Si bien es cierto que los valores de p son esencialmente pequenos; esto está en relacion con el hecho de que en tratamientos de radioterapia se utilizan blindajes para proteger las zonas adyacentes a las tumorales que reciben la radiación.
3.2. Regiones donde el tratamiento no es efectivo
Estas regiones se obtuvieron con algunos parametros donde los resultados son aquellos que describen un comportamiento en el que la poblacion de células cancerosas se impone sobre las celulas normales.
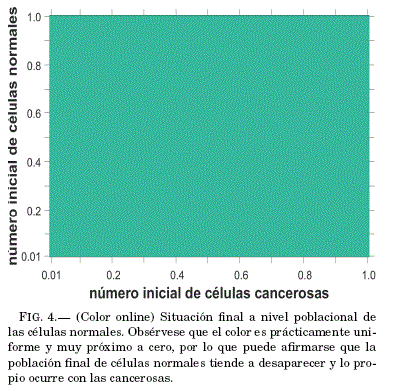
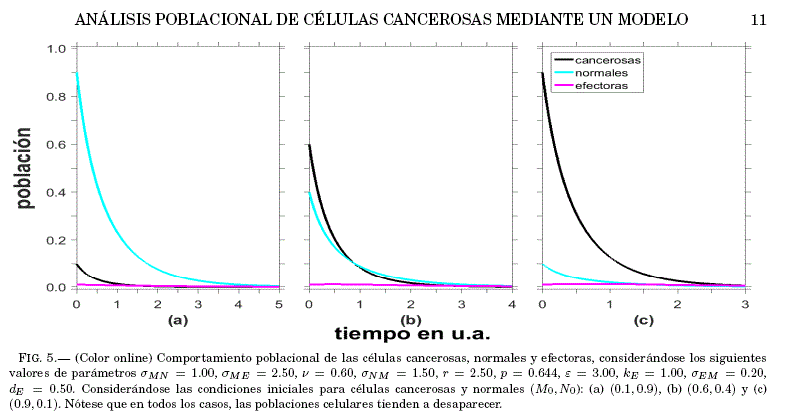
Con los siguientes parametros: σMN= 1.00, σME = 2.50, v = 0.60, σNM = 1.50, r = 2.50, p = 0.644, ε= 3.00, kE = 1.00, σEM = 0.20, dE = 0.50, se puede ver en la Fig. 4, la cuenca de atraccion que indica como la aplicación de la radiación elimina casi por completo la poblacion de células cancerosas sin importar las condiciones iniciales en lo que respecta a las poblaciones de celulas normales y cancerosas (M0,N0). Una situacion similar (que no se muestra) se presenta para la poblacion de células normales que tambien tiende a ser eliminada.
En la Fig. 5, se tienen las graficas correspondientes a las series temporales que describen el com-
portamiento poblacional mencionado anteriormente (eliminacion de todas las poblaciones celulares), estas graficas fueron generadas para diferentes condi-
ciones iniciales en las poblaciones de celulas. Esta situacion si bien es interesante desde el punto de vista de comportamiento dinamico del sistema, debe evitarse en un tratamiento de radioterapia.
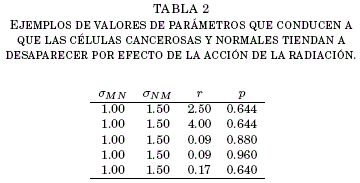
Muchas regiones con un comportamiento similar pueden ser encontradas realizando variaciones en sus condiciones, observese la Tabla 2.
En la Tabla 2 se tiene un conjunto de valores de parametros para los cuales se observa un efecto adverso en las celulas normales que son eliminadas junto con las cancerosas, en contraposicion al objetivo de optimizar un tratamiento por radioterapia, que elimine las celulas cancerosas y causando efectos mınimos en la población de células normales. Sin embargo, la informacion obtenida puede utilizarse para
buscar nuevas alternativas para el paciente ya sea modificando los valores de parametros o los de las condiciones iniciales.
3.3. Regiones con un comportamiento oscilatorio
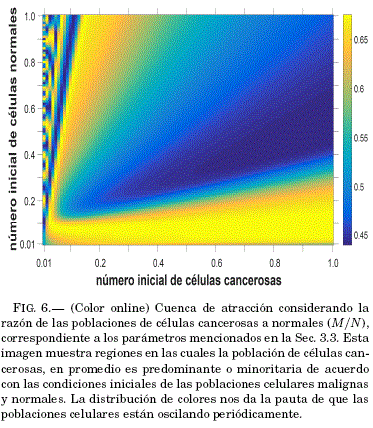
Este tipo de regiones muestra un comportamiento con diferentes valores de los promedios de la razon entre la poblacion de células cancerosas a la de normales; en otras palabras, existen oscilaciones de estas poblaciones que se reflejan en una distribucion de valores que forman una suerte de patron en la cuenca de atracción come se ve en la Fig. 6. La mencionada cuenca fue obtenida considerando los valores de parametros: σMN = 0.84, σME = 2.50, v = 0.60, σNM = 1.50, r = 0.17, p = 0.01, ε= 3, kE = 1.00, σEM = 0.20 y dE = 0.50.
La barra de colores en la Fig. 6 muestra las tendencias para las cuales se tiene ligera preponderancia de celulas normales y casi eliminación de células cancerosas (region azul); en contraposición, ocurre una predominancia de las celulas cancerosas sobre las normales en la region amarilla.
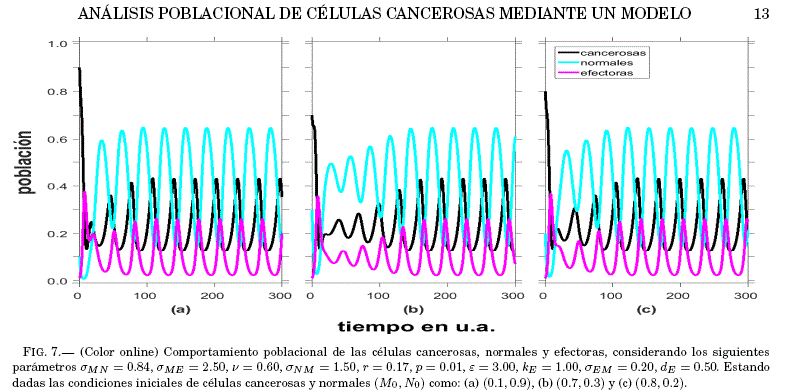
Para las condiciones mencionadas, las series temporales se muestran en la Fig. 7, donde se observa que para los ejemplos elegidos, las poblaciones celulares oscilan periodicamente y con valores mayores para las poblaciones de celulas normales. Este com-
portamiento puede deberse a que los valores de r son pequenos como para producir la eliminación total de las celulas. Si bien este comportamiento no cumple el requisito de nuestro objetivo (eliminacion de las celulas cancerosas sin afectar a las sanas); sin embargo, el conocimiento de estos comportamientos periodicos puede ser de utilidad al encarar un tratamiento con radiacion. Por ejemplo, si se conoce las características de estas oscilaciones, para una irradiacion posterior, podría escogerse el inicio de la misma cuando el numero de células cancerosas esté en un mınimo; así, se podría evitar que vuelva a crecer esta poblacion, con el consecuente aumento de la
probabilidad de eliminarla.
La Tabla 3, muestra algunos ejemplos de valores de parametros que permiten obtener comportamientos similares; es decir, oscilaciones periodicas de las poblaciones celulares.
3.4. Regiones con un comportamiento caótico
Estas son regiones cuyos resultados no estan claramente delimitados, las cuencas de atraccion presentan saltos aparentemente discretos en los resultados finales, una de las cuencas con estas características fue obtenida con las siguientes condiciones: σMN = 1.00, σME = 2.50, v = 0.60, σNM = 1.70, r = 0.17, p = 0.01, e = 3.00, kE = 1.00, σEM = 0.20, dE = 0.50.
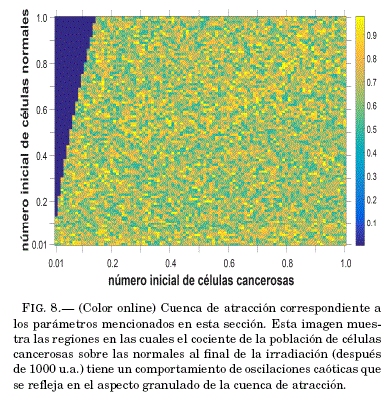
La cuenca de atraccion que representa los valores del promedio de la razón M/N segun las condiciones iniciales elegidas se muestra en la Fig. 8. En ella puede apreciarse que el cociente de la poblacion final de celulas cancerosas sobre las células normales toma valores que no generan una grafica uniforme, observandose regiones granuladas; es decir, se tiene en casi toda la cuenca, píxeles de diferentes colores que parece representar la rubrica del comportamiento caotico de las variaciones experimentadas por las poblaciones celulares.
Como puede verse en la Fig. 8, el resultado final para una poblacion alta de células cancerosas, no se muestra una regularidad aceptable, es decir para cada punto de la distribucion, los resultados finales presentan saltos discretos. Sin embargo, tambien se puede mencionar que para bajas cantidades de poblacion inicial de células normales la población de celulas cancerosas se elimina y la población de celulas normales sobrevive.
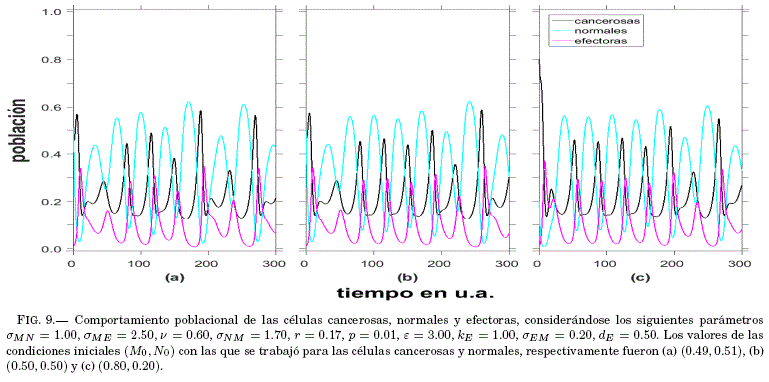
Las series temporales correspondientes a las condiciones mencionadas, pueden observarse en la Fig. 9, en ellas se verifica que no existe regularidad en los resultados finales luego del tratamiento. Por consiguiente, desde un punto de vista clínico, esta situacion de comportamiento caótico de las poblaciones deberıa evitarse. Una forma es aumentando la dosis, pero teniendo la precaucion de que esto no ocasione danos en las células normales.
La Tabla 4 muestra algunos valores de parametros para los cuales se tienen comportamientos conducentes a variaciones caoticas, en promedio, de las
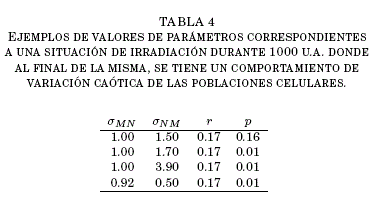
poblaciones celulares.
4. CONCLUSIONES Y PERSPECTIVAS
Considerando los resultados del presente estudio, se pudo ver la evolucion del comportamiento poblacional de los tres tipos de celulas bajo ciertas condiciones, sobre todo dandole importancia predominante a los aspectos relativos a la irradiacion. Se comenzo tomando como punto de partida los resultados del analisis de estabilidad obtenidos por Ramírez-Ávila (2017). Es decir, se tomaron valores de los parametros de las regiones de estabilidad que permitieron obtener la eliminacion de las celulas cancerosas afectando mínimamente a las celulas normales. Además, en varias de las situaciones analizadas tambien se observaron comportamientos periodicos y caóticos de las poblaciones celulares como en los trabajos de Galindo et al. (2015) y Gallas et al. (2014). Este aspecto se debe a que el comportamiento poblacional depende de las condiciones iniciales en concordancia con el analisis de Branco (2014). Consecuentemente, se puede inferir que si un paciente comienza con un tratamiento de radioterapia, cuando el cancer es detectado en un estadio temprano, los efectos de la radiacion sumados al efecto del sistema inmunologico, serán diferentes a otro paciente cuya deteccion de la patología se realizo, por ejemplo, en un cáncer terminal.
Si la radiación solamente actúa en las células cancerosas y no ası en las normales y considerando una poblacion inicial de células cancerosas alta (0.7), con un factor ligado a la radiacion de 0.12, aun se inducen comportamientos caoticos. Pero si la radiación se va incrementando, el sistema se estabiliza y la poblacion de células cancerosas se ve afectada por el efecto de la radiacion, haciendo que dicha población tienda a desaparecer. Este resultado implica que, a mayor radiacion, el sistema llega a una situación mas estable en menos tiempo.
Una de las situaciones analizadas considera el hecho de que, si la poblacion de células cancerosas es alta al inicio del tratamiento, el efecto de la radiacion toma mayor tiempo en manifestarse. Una situacion similar fue encontrada por Valle (2016), donde se considero la quimioterapia en lugar de la radiacion y pudo evidenciar que las poblaciones grandes de celulas cancerosas requieren mayor cantidad de dosis suministrada. Sin embargo, la dosis utilizada tambien tiene un efecto sobre las células
normales. En ese sentido, es importante considerar la aplicacion de dosis más bajas, pero aplicadas durante una mayor cantidad de tiempo, este tipo de tratamiento tendría un menor efecto sobre las celulas del sistema inmunológico situación afirmada por de Pillis et al. (2006). El resultado mas relevante obtenido es haber determinado los valores de parametros de control (mostrados en la Tabla 1) que conducen a la eliminacion de las células cancerosas sin afectar mayormente a las normales. Lo anterior puede ser un aspecto importante para la planificacion de los tratamientos por radioterapia, para que los mismos sean efectivos al margen de las condiciones iniciales en las poblaciones celulares. Este resultado permite vislumbrar un panorama alentador del uso del modelo.
La informacion analizada en el párrafo anterior, fue corroborada con las graficas de las series temporales elegidas (ver Fig. 3), donde pudo verificarse que, en cada situacion es posible eliminar las células cancerosas sin alterar o hacerlo mínimamente en la poblacion de células normales. Es importante mencionar que la poblacion de células del sistema inmunologico desaparece al final del tratamiento, cuando la poblacion de células tumorales es muy pequena, lo que se traduce en una inactivación de las celulas efectoras.
Dentro de los numerosos resultados que se obtuvieron, se pudo identificar condiciones en las que las celulas cancerosas se imponen sobre las células normales, bajo ciertos valores de parametros, las poblaciones iniciales de las celulas normales y cancerosas, no juegan ningun papel importante. En este punto aparentemente los resultados no son relevantes para el objetivo del trabajo de investigacion, pero en la practica pueden ser utilizados para desestimar un tratamiento por radioterapia y utilizar otro que pueda ser mas efectivo para el paciente. Por otro lado, los resultados obtenidos mostrando comportamientos periodico y caótico, indican que la aplicacion de la radiación no permite que las poblaciones celulares logren una estabilizacion, esto nos hace pensar que fraccionar la dosis de radiacion y aplicarla en situaciones en las que la poblacion de celulas cancerosas alcance un mínimo relativo o cuando la poblacion de células del sistema inmunologico se halle en un máximo relativo, pueden mejorar tambien el tratamiento tendiente a hacer desaparecer las celulas cancerosas.
Finalmente, es conveniente mencionar que como proyeccion se pretende analizar este sistema dinamico bajo la acción de otro tipo de tratamientos como la inmunoterapia. Aspectos relacionados con cronobiología pueden resultar interesantes dada la dependencia que se tiene con las condiciones iniciales. Considerar en el trabajo la posibilidad de hal-
lar las condiciones en las que la radiacion actúe en las celulas cancerosas y estas se eliminen en el menor tiempo posible, es otra de las perspectivas que pueden ser explotadas como continuacion de este trabajo de investigacion.
AGRADECIMIENTOS
Es importante el reconocimiento al Instituto de Investigaciones Físicas de la UMSA por haber facilitado el desarrollo de este proyecto. Tambien agradecemos a Paul Schultz del PIK-Potsdam por sus consejos y colaboracion en algunos de los aspectos compu-tacionales del trabajo.
Conflicto de intereses
Los autores declaran que no hay conflicto de intereses con respecto a la publicacion de éste documento.
REFERENCIAS
Abbas, A., Lichtman, A.H. & Pillai, S. 2015, Cellular and molecular immunology (Philadelphia: Saunders). [ Links ]
Belostotski, G. & Freedman, H. 2005, The European Physical Journal B 25, 447. [ Links ]
Bergonie, J. & Tribondeau, L. 1906, Comptes-Rendus de Séances de l'Académie des Sciences, 143, 983 [ Links ]
Branco, P. 2014, Comportamento Caótico em Modelos Matemáticos de Cáncer. Tesis de Maestrıa en Matemática Aplicada y Computacional, Universidade Estadual Paulista, Sao Paulo, Brasil. 78p. [ Links ]
Calvo, F. & Escude L. 1985, Revista Médica Universitaria Navarra 29, 110. [ Links ]
Castorina, P., Deisboeck, T., Gabriele, P. & Guiot, C. 2007, Radiation Research 168, 349. [ Links ]
de Pillis, L. & Radunskaya, A. 2003, Mathematical and Computer Modelling (37), 1221. [ Links ]
de Pillis, L., Gu, W. & Radunskaya, A. 2006, Journal of Theoretical Biology 238, 841. [ Links ]
Galindo, M. C., Nespoli, C. & Messias, M. 2015, Abstract and Applied Analysis Article ID 354918. [ Links ]
Galach, M. 2003, International Journal of Applied Mathematics and Computer Science 13(3): 395-406. [ Links ]
Gallas, M., Gallas, M. & Gallas, J. 2014, The European Physical Journal: Special Topics (223): 2131-2144. [ Links ]
Ghaffari, A., Bahmaie, B. & Nazari, M. 2016, Mathematical Methods in the Applied Sciences 39, 4603. [ Links ]
Gomez-Almaguer, D,, et al. 2010, Revista de Hematología11(1):40-62. [ Links ]
Isea, R. & K. Lonngren. 2015, International Journal of Public Health Research 3(6): 340-344. [ Links ]
Itik, M. & Banks, S. 2010, International Journal of Bifurcation and Chaos 20(1): 71-79. [ Links ]
Kuznetsov, V., Makalkin, I., Taylor, M. & Perelson, A. 1994, Bul-letin of Mathematical Biology 56(2): 295-321. [ Links ]
Liu, Z. & Yang, C., 2014, Computational and Mathematical Meth-ods in Medicine 12: 1-12. [ Links ]
Menchon, S. 2007, Modelado de las diversas etapas del crecimiento del cáncer y de algunas terapias antitumorales. Tesis doctoral en Fısica, Universidad Nacional de Córdova, Córdova. 114 p. [ Links ]
Ott, E. 1993, Chaos in dynamical systems (Cambridge: Cambridge University Press) [ Links ]
Pisarchik, A.N. & Feudel, U. 2014, Physics Reports 540: 167. [ Links ]
Ramírez-ávila, G.M. 2017, Revista Boliviana de Física 31, 25. [ Links ]
Rizo-Potau, D., Nájera-López, A. & Arenas-Prat M. 2016, Conocimientos básicos de oncología radioterápica para la enseñanza Pre-grado (Cuenca: Ediciones de la Universidad de Castilla La Mancha) (9). [ Links ]
Roman, J. M. 2007, Psicooncología 4(2), 301-310. [ Links ]
Pinar-Sedeno, B., Aguiar-Bujanda, D., Saez-Bravo, M. L., Ruiz-Alonso, A., & Lara-Jimenez, P. C. 2004, Biocáncer(1). [ Links ]
Valle, P. 2016, Estudio de la dinámica global de modelos matemáticos que describan la evolución de un modelo cancerígeno y sus mecanismos de evasión del sistema inmunológico. Tesis Doctoral en Ciencias, Instituto Politecnico Nacional, Ti-juana. 118 p. [ Links ]
Valle, P., Coria, L. & Starkov, K. 2014, Computación y Sistemas 18(4): 773. [ Links ]
Wintz, H. 1938, Radiology, 30, 35. [ Links ]