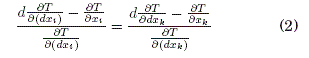Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
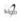 Similars in
SciELO
Similars in
SciELO
Share
Revista Boliviana de Física
On-line version ISSN 1562-3823
Revista Boliviana de Física vol.34 no.34 La Paz Nov. 2019
E. HISTORIA
Cien autores contra Einstein: una traduccion crítica parcial
A hundred authors against Einstein: a partial critical translation
Lucas Blitz Lozada Gobilard.
Carrera de Física
Universidad Mayor de San Andres
c. 27 Cota-Cota, Casilla de Correos 8635
La Paz, Bolivia
Resumen
La teoría de la relatividad de Einstein fue objeto de críticas de caracter científico, filósofico, gnoseológico e ideológico, principalmente en los primeros años posteriores a su publicación. En 1931, vio la luz en Leipzig, una obra titulada Cien autores contra Einstein (Hundert Au-toren gegen Einstein). A pesar que el libro paso al olvido sin mayor repercusión (no se hizo traduccion oficial alguna de su idioma original: el alemán) e incluso fue catalogado por Hans Reichenbach como "una acumulacion de errores ingenuos", es posible encontrar entre los pocos argumentos físicos y matematicos rigurosos, algunos que deban ser mencionados y discutidos. Así, es posible trascender los prejuicios personales y descubrir razonamientos logicos que sustentan algunas críticas, reforzando paradojicamente sin embargo, el valor científico y heurístico de la concepcion einsteniana de la relatividad. Tal es la posición de quienes aseguraron que los autores que criticaron a Einstein incurrieron en errores gruesos porque no comprendieron adecuadamente la concepcion de la relatividad. En este artículo traduzco el texto de uno de los autores que, en mi opinion, muestra el contenido del libro en general. Lo pongo al alcance del lector hispanohablante, ofreciendo tambien un comentario breve de los segmentos traducidos desde la perspectiva del conocimiento físico actual.
Codigo(s) PACS: 01.65.+g- 04.90.+e - 01.75.+m
Descriptores: Historia de la ciencia - Publicaciones sobre Teoría de la Relatividad - Ciencia y Sociedad
Abstract
Einstein's theory of relativity has been the subject to criticism: scientific, philosophical, epistemological and ideological, mainly in the first years after its publication. In 1931 in Leipzig a book called A Hundred Authors against Einstein (Hundert Autoren gegen Einstein) was printed. Despite the fact that the book was easily forgotten and had no major repercus-sion (an official translation of its original language, German, was never made) and it was even described by Hans Reichenbach as an "accumulation of naive errors". It is possible to find among the few rigorous physical and mathematical arguments, some that should be mentioned and discussed. Thus, it is feasible to transcend personal prejudices and discover the logic behind some of the criticisms, paradoxically reinforcing, the scientific and heuristic value of Einstein's conception of relativity. Such is the position of those who asserted that the authors who criticized Einstein made major errors because they did not properly under-stand the conception of relativity. In this article, the text of one of the authors who generally reflects the content of the book has been translated, so as to make it available to the Spanish-speaking reader. The article, also offers a brief commentary on the translated segments from the perspective of current physical knowledge.
Subject headings: History of science - Publications on Theory of Relativity - Science and Society
1. INTRODUCCION
El físico, historiador y filósofo de la ciencia estadounidense Thomas Kuhn diferencia lo que denomina ciencia normal de la revolución científica. La primera refiere la produccion de conocimiento como ejercicio relativamente rutinario, es el trabajo del día a día de científicos bajo la egida de algún paradigma; es decir según las estipulaciones explícitas e implícitas que posibilitan y restringen el conjunto de practicas científicas en algún momento histórico. Cuando surge una nueva teoría, lo mas probable es que sea asimilada a la ciencia normal, en la medida que no cuestione el conocimiento previo establecido que es asumido como valido por la comunidad respectiva. Pero cuando algun científico o filosofo piensa nuevos contenidos siguiendo pautas que no son aceptadas, cuando evidencia supuestos diferentes, elabora conceptos nuevos y se refiere a objetos cuya naturaleza parecía estar completamente entendida; tambien cuando propone relaciones ineditas entre los objetos, sucede lo que Kuhn denomina "revolucion científica". Se trata de una conmocion acumulada por las ideas y teorías que contradicen el paradigma instaurado, aunque sin destituirlo de manera absoluta. Es posible que una revolucion científica, segun Kuhn, se consuma durante largo tiempo y se precipite solo por la formulacion de una teoría; pero para que se de el cambio revolucionario, debe proyectar formalmente una nueva concepcion del universo. Al inicio, la teoría revolucionaria es rechazada por la comunidad que ve afectado su poder academico; a tal comunidad le disgustan los conceptos y las nuevas percepciones que hasta ese momento fueron inconcebibles y que la ciencia normal se empena en criticar o censurar. Sin embargo, la historia muestra que constatada la consistencia y verdad de la nueva teoría, se reconstituye la comunidad científica, siendo reemplazada por personas que aceptan, valoran y proyectan la teoría revolucionaria generando nuevo y fertil conocimiento que a la vez, revoluciona el viejo paradigma e instituye uno nuevo.

La revolución relativista, la einsteniana, constela las características principales de una revolucion científica segun Thomas Kuhn. Hoy día, la teoría de la relatividad es auto-consistente, se respalda con resultados experimentales y es la base de otras teorías exitosas como la electrodinamica cuántica. Sin embargo, inmediatamente despues de su publicación, varios autores se opusieron a ella con diversos argumentos; siendo intensas y multiples las expresiones de rechazo. El libro Cien autores contra Ein-stein (Hundert Autoren gegen Einstein) publicado en Leipzig y recopilado y escrito por Israel, Ruckhaber & Weinman (1931), es un manifiesto de rechazo inmediato a su teoría; incluye la coleccion de textos cortos de 29 autores con citas de publicaciones de otros 19 escritores que critican a Albert Einstein.
El presente artículo incluye a continuacion la traduccion al español del texto aportado por el profesor Dr. Jean-Marie Le Roux, un matematico francés. E-xisten dos razones que motivaron mi eleccion del Dr. Le Roux: en primer lugar, representa el empeno por demeritar a Einstein resumiendo con propiedad los argumentos expuestos por varios autores del libro. En segundo lugar, entre los 47 autores que forman la compilacion y que fueron citados, solamente hay tres matemáticos de profesión que se empeñan en argüir razonamientos lógico-matemáticos que invaliden la teoría de la relativiad: uno de ellos es Le Roux. Los otros dos matematicos son Emanuel Lasker y Hjal-mar Mellin, destacando, ademas el físico Karl Strehl.
2. TRADUCCION
A continuacion se presenta la traducción al español de los argumentos del Dr. Jean-Marie Le Roux expuestos en la obra referida (traduccion del francés al aleman por el Dr. Erick Ruckhaber, uno de los autores principales del libro). Las crıticas del matematico francés al físico aleman se presentan en nueve puntos. El presente artículo traduce cada uno de tales puntos, seguido de un comentario breve con base en conocimientos actuales del tema en cuestion. Los comentarios recopilan la bibliografía específica sobre cada punto ofreciendo un panorama general. Ademas, son frecuentes las referencias a la obra de Hans Reichenbach, físico y logico alemán mencionado en el resumen. No obstante, debo decir que de ningun modo me considero especialista en relatividad, ni trato de desmeritar al autor o desacreditar los alegatos expuestos en el texto traducido.

1. EL QUIEBRE DE LA TEORÍA DE LA RELATIVIDAD. La teoría de la relatividad (TR) 1 de Einstein ha provocado un vıvido movimiento mental y ha iniciado varias investigaciones teóricas y experimentales que han contribuido al avance de la ciencia. La teoría en si misma no resiste una prueba exhaustiva. A la luz de la crıtica, se muestra que la sıntesis dada es un resplandor vacıo, que solo se puede preservar en una semioscuridad proteccionista favorable. La incoherencia de los argumentos y la puerilidad de las hipotesis son del mismo tipo. Las inferencias a veces no tienen relación con las premisas y los componentes basicos de los calculos en el resultado adquieren un significado que no se corresponde con la definición en los datos subyacentes. Quizás se puede pasar por alto los errores metodológicos, si los resultados trajesen consigo un verdadero provecho para nuestro conocimiento. Lamentablemente, este no es el caso. Uno u otro de los resultados obtenidos son independientes de la teorıa y de ninguna manera sirven para respaldarla .
Se sabe que la TR especial se creo con motivo del experimento de Michelson. Pero su propio autor no entendio los resultados de este experimento correctamente. Ha extraıdo de ellos conclusiones que en realidad no están incluidas. ¡Después trató de explicar estas conclusiones mediante una serie de hipótesis que se contradicen entre sı y no tienen relación con el fenómeno!
La teoría gravitatoria tambien es muy extrana. Aquí, sin embargo, viene el defecto del gigantesco engaño en la supuesta explicación de la progresión secular del movimiento del perihelio de Mercurio. La magnitud observada de dicho movimiento es de aproximadamente 374'' . La teorıa de Einstein da un desfase de aproximadamente 42''. La teoría de Newton predice un valor de 336'' para este movimiento. Para deducir la superioridad de la doctrina de Einstein, se necesita algo más que la autocomplacencia más ciega y aberrante .
La impotencia de la TR en este sentido se debe a toda su composición. La teorıa toma su propio principio como el punto de partida de sí misma al comprometerse a representar el movimiento de los cuerpos mediante medidas geodésicas en forma de diferenciales cuadraticos con cuatro variables, por espacio-tiempo con cuatro dimensiones. Esta hipótesis está en contradicción con la gravitación.
Los intentos de los matematicos, que son más concienzudos que clarividentes, de reconciliar entre sí las cosas logicamente incompatibles, son forzosamente rechazados y no tienen exito. En los aproximadamente quince anos desde que se fundó la TR general, ha sido imposible deducir de ella una representacion aproximada del movimiento del sistema solar o de cualquier otro sistema. Las promesas hechas no se han cumplido, esto es un fracaso significativo.
El texto no contiene referencias de los datos mencionados en este punto. Sin embargo, respecto a la precesion del perihelio de Mercurio existe bastante literatura; por ejemplo, en el libro Theory of Relativity, de Wolfgang Pauli (1958) se lee:
"Las dos consecuencias de la teoría de gravitacion de Einstein aca desarrolladas admiten ambas una revision experimental. Para la precesión del perihelio2 (...), esta solo es medible en el caso de Mercurio, donde las condiciones son particularmente favorables debido a su corta distancia al Sol y la grande excentricidad de su orbita. El valor teórico de la precesion en un siglo es
Se sabe entre los astronomos desde tiempos de Leverrier que un residuo esta presente en la precesion del perihelio de Mercurio, que no puede ser causado por perturbaciones debidas a otros planetas. De acuerdo a los calculos renovados de Newcomb, es de magnitud:
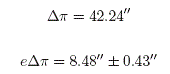
Sobre este punto, debo decir que no se aclara si los datos mencionados por el Dr. Le Roux hacen referencia a una precesion secular, a una precesión teórica o de otro tipo.
La version original del libro de Pauli fue publicada en aleman en 1921. Se sabe que el Dr. Le Roux no hablaba aleman, porque de otro modo no hubiese necesitado un traductor (Ruckhaber) para su aporte a Cien autores contra Einstein. Una version en inglés fue publicada en 1958, y aunque se desconoce si Le Roux estaba al tanto de las cifras presentadas en el libro de Pauli, vale decir que en la pagina de Wikipedia del matematico francés se dice que él editó el artıculo Wahrscheinlichkeitstheorie, de Emanuel Czuber (ver Jean-Marie Le Roux en Wikipedia). Curiosamente, fue en esa enciclopedia que Pauli publico su trabajo sobre relatividad, dando la noción que Le Roux sí estaba enterado del trabajo. Por todo lo mencionado, es pertinente decir que nunca cambio su criterio de oposicion de la teoría de la relatividad de Einstein (este no es el caso de todos los autores que aportan al libro).
Si el experimento de Albert Abraham Michelson fue el motivo de la creacion de la TR, es un tema que tratare en el siguiente punto.
2. LA PRUEBA DE MICHELSON. A partir del experimento de Michelson, la TR concluye que la velocidad relativa de propagacion de la luz es la misma para el observador en todas las direcciones. Esta conclusion es incorrecta. La isotropia de la onda de interferencia no incluye la de la onda de propagación. A lo sumo, se puede concluir que el medio en el que la luz se propaga, sea éter o llamado de otra forma, es homogéneo e isótropo respecto a un sistema de referencia dado solo bajo ciertas condiciones.
Si se admite que el éter esta influido por la gravedad, entonces incluso la ley de propagacion puede satisfacer las siguientes condiciones:
a) Hay un sistema de referencia S, tal que los medios de propagacion son homogéneos e isotrópicos con respecto a S en cualquier region suficientemente alejada de los cuerpos.
b) Para cada fuente de luz inmutablemente unida al mismo sistema de referencia, la onda de interferencia es isotrópica en un area particular.
c) Para cada fuente de luz, transportada por y ligada a una masa material, la onda de interferencia tambien es isotrópica en un área especifica.
Hay un número interminable de soluciones cuyas caracterısticas comunes son fáciles de determinar. Por lo tanto, el análisis exacto del fenomeno no da paso a las implicaciones peculiares que forman la base de la relatividad especial. Los resultados muy precisos de los nuevos experimentos de Miller son de gran interes porque pueden ayudarnos a conocer la influencia de la materia en las condiciones de propagacion de la luz.
Vale decir que el Dr. Le Roux es el unico autor que en el libro hace mencion a sistemas de referencia físicos. Por otra parte, decir que la TR concluye tesis a partir del experimento de Michelson es osado. Aunque mucha literatura -principalmente pedagogica- presenta la teoría de la relatividad como el proposito de explicar los resultados del experimento de Michelson, aquı se encuentra uno de los genuinos problemas historicos de la física.
En la primera parte de su artículo titulado "Einstein and the Crucial Experiment", Gerald Holton (1969), despues de hacer un exhaustivo análisis y tratar el problema, concluye que el experimento de Michelson no fue crucial para Einstein en el desarrollo de la teoría de la relatividad, a pesar de la insistencia de tantos autores que arguyen lo contrario.
Respecto a los incisos a), b) y c) de este punto, resulta inmediato asociar el sistema de referencia mencionado por Le Roux con la teoría del arrastre del eter. Esta sustancia hipotética, supuesto medio de propagacion de la luz, resulta en un sistema de referencia privilegiado. La relatividad especial por sí sola prescinde de la hipotesis del éter. Es más, esta cuestion fue desbancada por la teoría general de la relatividad y la hipotesis fue anulada por posteriores resultados experimentales. Para mas detalle sobre la teoría del arrastre del eter ver, por ejemplo, Stokes (1845) y acerca de la vasta validacion experimental de la teorıa de la relatividad, recomiendo consultar Clifford (2014).
En el ultimo párrafo, el Dr. Le Roux refiere a los trabajos de Dayton Miller, fısico norteamericano y ferviente opositor de la TR de Einstein que trabajo con Edward Morley en el desarrollo de su inter-ferometro, entre otras cosas. Miller intentó detectar experimentalmente eter luminoso, pero los resultados en algunas de sus publicaciones (ver, por ejemplo, Eddy, Morley & Miller (1898)), por el contrario, sirvieron para validar la TR de Einstein. Miller se empecino en aumentar la precisión de sus experimentos para mostrar la existencia de eter luminoso, lo que le llevo a fabricar el interferómetro más preciso jamas construido hasta entonces.
3. LA EXPLICACIÓN RELATIVISTA DEL EXPERIMENTO DE MICHELSON. Luego de obtener conclusiones incorrectas del experimento de Michelson, la escuela relativista intenta explicarlas. Dado que la ecuación con derivadas parciales para la propagación de las ondas para la transformación analítica, que representa una traslación lineal regular no es válida, se cambia el significado de las palabras. La transformación de Voigt-Lorentz, que mantiene la forma analítica de la ecuacion en cuestión, es renombrada "traslacion".
Esta es una treta ridicula. La traslacion es una cosa y las transformaciones de Voigt-Lorentz son otra. Hay un grupo de traslaciones así como hay un grupo de
Voigt-Lorentz. Ambos grupos tienen su propio significado y área de estudio en las matemáticas. Como se trata de un asunto de definiciones, no se las puede mezclar.
Con el proposito de trabajar con el grupo de Voigt-Lorentz, Einstein adopta dos sistemas de referencia: cada uno de e-llos tiene un observador con un conjunto completo de escalas y relojes. Cada uno de ellos realiza mediciones de longitud en su propio sistema, colocando las escalas, de acuerdo con los métodos de la geometría euclidiana. Los observadores y los objetos tienen una existencia permanente e incluso, como se le llama, pueden pasar de un sistema a otro. Finalmente, la relacion entre las coordenadas de uno y el mismo punto de evento relacionado con ambos sistemas está establecida por las formulas de Lorentz.
Es inmediatamente obvio que estas hipótesis no tienen nada en común con las condiciones del experimento de Michel-son, donde solo hay un observador que no tiene que consultar su reloj ni fijar el valor numérico de la velocidad de la luz.
El Dr. Le Roux no expone explıcitamente la ecuacion con derivadas parciales a la que se refiere en este punto, aunque resulta logico asumir que se trata de una ecuacion de onda. Dos años después de la publicacion de 100 Autoren gegen Einstein, Le Roux (1933) publico un trabajo en francés titulado El principio de la relatividad y la ley de gravitación, donde expone detalladamente sus alegatos y razonamientos matematicos para desacreditar e invalidar la teoría de la relatividad de Einstein.
En un espacio-tiempo 4D, las transformaciones de Lorentz son "rotaciones" y no "traslaciones". El autor parece confundir estos dos conceptos y asume como correctas las transformaciones de Voigt. Estas difieren de las transformaciones de Lorentz y pueden mencionarse de forma sencilla como sigue:
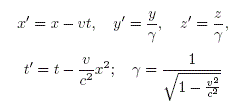
Para mayor detalle, consultar a Ernst & Hsu (2001).
Respecto a este trabajo, cabe senalarse que alrededor de 1886, el físico aleman Woldemar Voigt investigo la perspectiva de los cuerpos en movimiento en la misma forma como Albert Einstein formulo la TR.

Por otro lado, Hendrik Lorentz fue un físico neerlandes, ganador del premio Nobel de Física en 1902. En su artículo, "Special Relativity", O'Connor & Robertson (1996) resumen el papel que jugaron Voigt y Lorentz en la formulacion de la TR:
"Lorentz escribio un artículo en 1886 donde criticaba el experimento de Michelson, apelando a la poca precision del mismo. Michelson fue persuadido por William Thomson, entre otros, a repetir el experimento y así lo hizo con Morley. En los resultados parecıa que la velocidad de la luz era independiente de la velocidad del observador.
Tambien en 1887 Voigt escribió las transformaciones que llevan su nombre y mostro que ciertas ecuaciones eran invariantes bajo estas transformaciones. Con un factor de escala diferente, tales transformaciones son conocidas como las ecuaciones de Lorentz y el grupo de transformaciones de Lorentz proporciona la geometría de la relatividad especial. Todo esto era desconocido para Voigt cuando escribio las transformaciones."
Aunque estas transformaciones se hallan en el estudio de teorıa de relatividad, la motivación original de Lorentz radicaba en el intento de resolver las inconsistencias entre la mecanica clásica y el electromagnetismo. En este sentido, uno de los sistemas de referencia de Lorentz fue el eter luminoso. El factor de escala mencionado en el texto de O'Connor y Robertson refiere a una constante multiplicativa en la transformacion de un operador d'alambertiano al pasar de un sistema de referencia a otro:
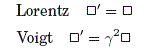
Así, la denominada "invariancia" de las transformaciones de Lorentz se da con una diferencia de una constante multiplicativa. Para mayor detalle, consultar Kittel (1971).

Los resultados experimentales, donde destacan los realizados por Michelson, mostraron que este factor no esta presente, lo que parece contradecir parcialmente el punto 2. Es por esto, en parte, que muchos autores consideran que los resultados del experimento de Michelson fueron prueba experimental suficiente para validar la teoría de la relatividad, a pesar de haber sido obtenidos mucho antes del desarrollo de Einstein.
4. INCOMPATIBILIDAD DE LAS CONDICIONES DE EINSTEIN. Pero aún más: las hipótesis son lógicamente incompatibles entre si.
Puede haber dos sistemas con las variables S(x, y, z, t) y S' (x', y', z', t') que se corresponden entre si según las fórmulas de Lorentz. Si se va a fijar un punto en el sistema S', entonces x', y', z' deben ser constantes mientras que t' permanece arbitrario. Entonces, la ecuación que determina t' no juega ningún papel.
En estas circunstancias, todos los puntos vinculados a S' se someten a una traslación directa y uniforme con respecto a S'; pero las variables x', y', z' no representan coordenadas cartesianas con angulos rectos tal como ocurre en el sistema S. Lo mismo es obviamente cierto si se toma x, y, z como fijos y t como arbitrario .
Einstein no distinguio entre los valores instantáneos fijos y los valores variables de t yt', entre un objeto permanente y un evento momentaneo.
Pero los observadores, sus estandares y relojes en el sistema al que estan vinculados deben considerarse como cosas permanentes .
De acuerdo con una de las hipotesis básicas de Einstein sobre la longitud de masa en uno de los sistemas, dos objetos similares en el mismo sistema se relacionan entre si mediante una transformación euclidiana realizada sobre las variables de ese sistema.
Por otro lado, de acuerdo con las hipótesis formuladas, los observadores, los sistemas de coordenadas y los relojes se referencian mutuamente de un sistema a otro. El total de estas suposiciones requeriría que la transformacion de una sustitución euclidiana sea invariante, lo cual no es el caso.
La interpretación einsteniana del grupo de Lorentz encuentra pues una contradiccion lógica. Toda la TR especial se basa en este frágil fundamento.
Sería interesante disponer del detalle de los sistemas S y S', señalándose la relación entre los mismos y explicitandose el ejercicio que mantenga una variable arbitraria y las otras constantes, segun lo mencionado por el Dr. Le Roux. Quizas de este modo sería ilustrativo y sencillo comparar los sistemas mencionados, como los que se encuentran en la teoría de la relatividad de Einstein.
No obstante, aludiendo a los argumentos de Le Roux mencionados en el primer parrafo, podría ocurrir que en las transformaciones de Lorentz:
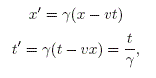
x' adopte un valor constante arbitrario, siendo posible que tome valor nulo. Por otro lado, en la ecuación ![]() , el factor
, el factor ![]() es perfectamente conocido. De esta forma, t' asume un valor bien definido a traves de la transformación de Lorentz: se trata de la dilatacion del tiempo, donde t' corresponde al tiempo propio.
es perfectamente conocido. De esta forma, t' asume un valor bien definido a traves de la transformación de Lorentz: se trata de la dilatacion del tiempo, donde t' corresponde al tiempo propio.
En su trabajo Einstein y la Geometría, Álvarez-Gaume & Vázquez-Mozo (2005) proporcionan de manera clara conceptos esenciales en la TR de Einstein. En la seccion "La Geometría del Espacio-Tiempo", escriben:
"El principio de relatividad galileano supone la existencia de un conjunto infinito de sistemas de referencia inerciales (esto es, sistemas de referencia en los que se satisface la ley de la inercia) y que necesariamente se mueven unos con respecto a los otros con velocidad constante. Este principio afirma que las leyes de la mecanica toman la misma forma en todos los sistemas inerciales (...). En particular, en la relatividad galileana el tiempo no cambia al pasar de un sistema de referencia inercial a otro mas allá del cambio producido por una diferente eleccion en el origen de los tiempos: los relojes de dos observadores inerciales no tiene por que marcar la misma hora, pero sı medirán el mismo intervalo temporal transcurrido entre dos sucesos".

Tiempo y simultaneidad son dos conceptos esenciales en la TR. En el capítulo IX: "¿Que es el tiempo?" del libro La filosofa científica, Hans Re-ichenbach (1951) -quien califico a Hundert Autoren gegen Einstein con el adjetivo de "errores ingenuos"-escribe:
"La definicion de sucesión temporal tiene una pareja en la definicion de simultaneidad. Llamamos simultaneos a dos acontecimientos cuando ninguno de ellos es anterior o posterior al otro. El problema de la simultaneidad lleva a consecuencias peculiares cuando se comparan acontecimientos ocurridos en lugares diferentes. Este problema ha adquirido fama gracias al analisis de Einstein.
Cuando queremos conocer el tiempo en que ocurre un acontecimiento lejano hacemos uso de una senal que nos transmite el mensaje de la realizacion del acontecimiento. Pero como la señal tarda en llega, el momento en que la recibimos no es identico al tiempo en que ocurrió el acontecimiento y que es el que nosotros queremos averiguar. Esto es cosa bien conocida en el caso de senales sonoras."
Desarrollar la transformacion de una 'sustitución euclidiana' y confirmar por que debería ser invariante segun las hipótesis de Einstein es un trabajo que cualquier persona que desee entender a profundidad el punto 4 del Dr. Le Roux debería realizar. No obstante, huelga decir que la carencia de una definicion concreta de conceptos tales como 'longitud de masa' o 'sustitucion euclidiana' dificulta seriamente la comprension física de este punto.
5. ESPACIO Y ESPACIOS. En la TR general hay una mezcla de dos cosas que los matematicos suelen llamar erróneamente con el mismo nombre: el espacio geometrico y los espacios analíticos.
En los casos en que se producen n variables 3, los analistas a menudo dan a un sistema de valores numéricos asignados a estas variables, el nombre de "punto analítico" y y a la suma de estos puntos el nombre de "espacio analítico". El número de dimensiones del espacio analítico considerado es el número de variables que lo componen. Estas definiciones son puramente analíticas e independientes de los significados concretos de las variables dadas.
El punto de vista del geómetra es diferente. Para él, el número de dimensiones no es una propiedad del espacio, sino una propiedad del elemento de espacio.
Esto requiere una explicación. La posición de un punto geométrico está determinada por tres coordenadas. La totalidad de las posiciones de los puntos geométricos formaría ası un espacio analítico tridimensional. Pero una recta está determinada por cuatro números, que asimismo son tambien llamados sus coordenadas; la posición de un solido rígido esta determinada por seis coordenadas, y ası sucesivamente. Si se considera a la recta como un elemento, la totalidad de las posiciones posibles forma un espacio analítico de cuatro dimensiones (espacio ordenado de Plücker) . El conjunto de las posiciones de un sólido rígido también determinarıa un espacio analítico de seis dimensiones.
Para el geometra, la ubicación de los puntos es la misma que la de la recta o el sólido: siempre es el mismo espacio.
Por lo tanto, el espacio considerado como un lugar en el sentido del geómetra no tiene un numero definido de dimensiones.
La mecánica clásica considera sistemas cuya posición depende de cualquier número n de parámetros. El total de las posibles posiciones de este sistema forma un espacio analítico de n dimensiones; el lugar de estas posibles ubicaciones siempre pertenece al mismo espacio indeterminado del geometra.
El punto de un evento en el sentido relativista esta determinado por tres coordenadas de posición asociadas con un valor de tiempo. Su totalidad forma un espacio analıtico tetra-dimensional. Pero cuando el evento se compone de la consideración simultánea de dos posiciones de puntos y un valor de tiempo, el todo forma un espacio analítico de siete dimensiones.
El total de las conexiones posibles de dos puntos de evento completamente independientes formaría un espacio analítico de ocho dimensiones.
Otros ejemplos son superfluos. El aquí dado es suficiente para aclarar que diferencia esencial existe pare el geometra entre el espacio de lugar y los espacios totales. Hay dos términos diferentes que reciben el mismo nombre.
En la terminología moderna, suele entenderse el llamado espacio analítico como "espacio de configuraciones". En la relatividad general, la geometrıa del espacio-tiempo no es igual al espacio de configuraciones de la mecanica. El primero corresponde a un espacio físico y el segundo al mencionado en este punto por el autor, quien parece confundirlos.
Como determina el Dr. Le Roux en este punto el numero de dimensiones de un espacio analítico detalladamente, segun sea el caso, es algo que escapa de mi conocimiento. Insto para que algun lector experto en el tema ponga especial atencion a este punto. No obstante, parece intuitivo asimilar que las siete dimensiones a las que se refiere el autor corresponden a 2 eventos localizados en un espacio de configuraciones con coordenadas (x, y, z) y (x', y', z') respectivamente, y un tiempo absoluto compartido: (t).
Acerca de la naturaleza del espacio, que revela la relatividad general, en su libro La filosofía científica, al mencionar la teoría de Einstein en el capıtulo "La Evolución", Reichenbach (1951) escribe:
"Segun Einstein el universo no es infinito, sino un espacio riemanniano cerrado de tipo esferico. Esto no quiere decir que el universo se halle encerrado dentro de una especie de cascaron esférico, encerrado a su vez dentro de un espacio infinito. Quiere decir que el espacio total es finito, sin linde alguno. Dondequiera que nos encontremos, siempre habra espacio alrededor de nosotros en todas direcciones, y no podra verse ningún fin; pero si avanzamos en lınea recta, algún día regresaremos a nuestro punto de partida por la direccion opuesta.
Podemos comparar estas propiedades tridimensionales del espacio con las propiedades observables de la superficie bidimensional de la Tierra, que en todas partes muestra el aspecto de una superficie practicamente plana, en tanto que la totalidad de estas areas es cerrada, de modo que quien avance en lınea recta regresará finalmente a su punto de partida. Como todas las demas concepciones de la geometrıa no euclidiana, el espacio cerrado es susceptible de representacion, aun cuando esta representacion requiere alguna práctica para vencer el condicionamiento de un medio geometrico más simple."
Adicionalmente, Álvarez-Gaumé & Vázquez-Mozo (2005) ofrecen una explicacion sencilla y completa sobre la geometría usada por Einstein en sus trabajos sobre la teoría de la relatividad. En la introduccion de Einstein y la Geometría escriben:
"Tuvieron que pasar no obstante 300 anos desde el intento de Kepler para que la geometrizacion de la Fısica viniera de la mano de la teoría de la relatividad einsteiniana. A pesar de la fascinacion infantil de Einstein con la geometría no fue el quien dio el primer paso. En su celebérrimo artıculo de junio de 1905 la relatividad es presentada de manera física a traves de relojes y reglas. Fue el matematico suizo Hermann Minkowski quien en 1908 se dio cuenta de que las transformaciones entre los diferentes sistemas de referencia inerciales se podían entender geometricamente como ciertos cambios de coordenadas en el "espacio-tiempo", un hiperespacio de cuatro dimensiones en las que tres de ellas se identifican con las dimensiones espaciales habituales mientras que la cuarta corresponde al tiempo."

Mas adelante, Álvarez-Gaumé y Vázquez-Mozo explican las características del espacio de Minkowski y como la geometría en la teoría de la relatividad especial se desarrolla asumiendo tales caraterísticas. Quizas en este punto y en
los siguientes se fundamentan los razonamientos matematicos del Dr. Le Roux, que usualmente no son considerados en el ambito de la física. Tambien es posible que el pensamiento de matematico puro no permitio al Dr. Le Roux desplegar el olfato físico para captar y asimilar los postulados de la TR.
Respecto a la diferencia mencionada en el ultimo parrafo del punto, la naturaleza de la geometría empleada en la TR ha mostrado que Einstein sı comprendıa y diferenciaba correctamente estos conceptos.
6. EL ESPACIO-TIEMPO RELATIVISTA Y EL ESPACIO ANALÍTICO DE LA GRAVEDAD NEWTONIANA. La relatividad tiene solo un espacio-tiempo tetradimensional a la vista, que analiza en forma de diferenciales cuadráticos; esto debería jugar un papel similar al elemento de línea de una superficie en geometrıa.
Luego, la fuerza de gravedad estarıa determinada por esta forma cuadratica. El movimiento natural de un punto estaría representado por una linea geodésica de la forma diferencial en cuestion. Esta linea geodésica sería su linea de mundo, de tal forma que cada movimiento corresponde a una linea geodésica.
Hay algo similar en la mecánica clásica. El principio de mínima acción lleva a la suposicion de que el movimiento de un sistema se basa en una lınea geodésica en forma de diferenciales cuadráticos. Pero uno tiene en mente el movimiento de un sistema completo que se considera como un todo sólido y ya no es el de un solo elemento .
La forma cuadrática comprende tantas variables como sea necesario para determinar la posición del sistema, y es el movimiento del todo lo que está representado por una linea de la forma en cuestion.
Si se piensa, por ejemplo, que el universo esta constituido por un conjunto de n puntos de masa, la posición de todo dependera de 3n variables. El espacio analítico correspondiente tendrá 3n dimensiones. El tiempo no es una coordenada complementaria, ya que el movimiento de un reloj, sea cual sea su naturaleza, es independiente de los movimientos de los cuerpos en el universo.
La forma cuadrática mencionada es la siguiente:
donde U denota una función de las coordenadas del sistema. El cálculo implica la introduccion de una variable auxiliar t, que esta determinada por la ecuación:
Esto permite volver las ecuaciones diferenciales geodesicas a la forma usual de las ecuaciones de la mecánica. Esta variable auxiliar t es el tiempo canonico de la mecánica clásica.
El sistema de referencia canónico es aquel para el cual la energía cinetica del universo observable es mínima.
Si se determina U mediante una mini-mizacion de dicha energía, se encuentra:
donde mi y mk denotan las masas de dos elementos y rjk su distancia. Esta es la primera ley de Newton. Las ecuaciones de movimiento, entonces tienen la siguiente forma:
Estas ecuaciones contienen no solo las coordenadas del punto considerado, sino tambien las de todos los otros puntos del sistema, dando así la unidad al todo.
Un hecho interesante de la relatividad, que revela la mecánica clasica, pero escapo de la escuela de Einstein, es el carácter relativo del principio de igual acción y reaccion. Este principio no expresa una propiedad de la materia: es una propiedad que proviene de la elección del sistema de referencia.
En el ambito de la geometría, una lınea geodésica es aquella que une dos puntos en una superficie dada y tiene longitud mínima. Ademas, la línea geodesica está contenida dentro de la mencionada superficie. Una curva temporal es aquella que en cualquiera de sus puntos su vector tangente es un vector temporal. Ası, una geodésica temporal es una curva temporal que ademas es geodésica. Para mayor detalle, ver Nomizu (1996). Las curvas geodesicas temporales han servido para ilustrar el comportamiento predicho por la teoría general de la relatividad con fuerte validacion experimental en los ultimos años. En particular, recomiendo los textos de Clifford (2014), quien ha dedicado anos de su vida a recopilar la evidencia experimental que ha servido como sustento para validar y dar credito a la teoría de la relatividad.
Al referirse a la similitud con la mecanica clásica, Le Roux parece no objetar el razonamiento de la TR, pero sí parece cuestionar su originalidad. Nuevamente, la percepcion del Universo para el Dr. Le Roux esta dada en un espacio de configuraciones, como evidencian las mencionadas 3n variables. Por otro lado, la propiedad del tiempo como parametro absoluto fue discutida en el punto 4.
Aunque la naturaleza de la función U no es determinada a priori, puede resultar ilustrativo para el lector expresarla como variable despejada de la segunda ecuacion de este punto, de tal modo que adquiere la forma de energía cinetica:
![]()
Por otra parte, lo que el autor llama en este punto primera ley de Newton se refiere a la ley de gravitacion universal. Confío en que este error se produjo por una distraccion en la traducción o la transcripcion por parte de Ruckhaber.
Sería ilustrativo disponer de un procedimiento detallado que explique la obtencion de las ecuaciones (1). Lamentablemente, en la compilacion Cien autores contra Einstein es frecuente referir las ecuaciones que desmeritan la TR sin presentar el proceso logico o matemático realizado para obtenerlas. Los detalles se hallan mayoritariamente en el trabajo de Le Roux publicado en 1933, al que hago mencion en el comentario del punto 3.
No obstante, es posible deducir las ecuaciones a partir del principio variacional de Jacobi, quien establecio que en la integral de la acción, el tiempo debe ser eliminado por el principio de vis viva, y todo se reduce a elementos de espacio. Para mas detalle al respecto, recomiendo la lectura de Jour-dain (1912). Esto explica la ausencia inicial de un diferencial de tiempo en las ecuaciones, que termina siendo definido de manera astuta, como mejor le parezca al autor. En relatividad general, el proceso de extremizar el diferencial para obtener las geodesicas es similar, donde el parámetro corresponde al tiempo propio.
Aunque el supuesto caracter relativo del principio de accion y reacción, mencionado por Le Roux, resulto algo inédito para mí y mis futuros colegas fısicos con los que pude discutir sobre este trabajo, sí es evidente una tendencia por parte del autor a asimilar y defender la validez absoluta del principio de Mach. La primera pauta de esto se halla en el ultimo párrafo de este punto y se refuerza en los argumentos de los puntos siguientes.
7. SOBRE LA IMPOSIBILIDAD DE REPRESENTAR LOS FENÓMENOS DE LA GRAVITACIÓN MEDIANTE LA TEORÍA DE EINSTEIN. Todavıa queda por demostrar que es imposible representar los fenomenos de gravitación, si se parte de la hipotesis básica de Einstein.
Sea t una forma cuadratica de diferenciales de cuatro variables x1, x2, x3, x4. Las ecuaciones de las líneas geodésicas de esta forma se pueden escribir de la siguiente manera:
Se permite que tres de las coordenadas se expresen como funcion de la cuarta y seis constantes de integracion arbitrarias. Dos soluciones difieren solo en valores numéricos de estas seis constantes.
Consideramos dos soluciones que representan los movimientos de dos cuerpos arbitrarios. Sea y1, y2, y3, y4 las coordenadas de los elementos de la primera, mientras que z1, z2, z3, z4 las de la segunda. Se puede considerar, por ejemplo, que y1, y2, y3 se expresan como una funcion de yA, y también z1, z2, z3 como una función de z4. Pero no hay necesariamente una relación entre y4 y z4: En general, no hay una relación necesaria del tipo elemento a elemento entre dos lineas geodesicas. Evidentemente, esto podría hacerse, estableciendo y4=z4=t, donde t denota un tiempo. Este acuerdo de ninguna manera es necesario. En las ecuaciones diferenciales (2) , nada cambiaría si establecemos y4=t para la primera linea y z4=t + α. para la segunda, donde a. denota una constante arbitraria.
La ausencia de una relación regular entre los puntos de evento de dos lıneas geodesicas diferentes es la razón principal por la cual la teorıa de Einstein es inadecuada para representar un fenómeno de la gravitacion. Es posible derivar de la teorıa de ecuaciones diferenciales que se aproximarán más o menos a las del movimiento de un solo punto; pero nunca se podra deducir a partir de ahí las ecuaciones para el movimiento de un sistema fijo, sin importar cual. El fracaso de los experimentos realizados en este sentido no se debe a la dificultad del problema o la incapacidad de los autores, sino a la contradiccion esencial entre el principio de la teoría de Einstein y la consistencia del conocimiento establecido .
Ni siquiera ha sido posible establecer las ecuaciones para el movimiento de un sistema de dos cuerpos basado en un sistema de referencia que no considera a uno de estos cuerpos como punto de partida.
El secreto de esta incapacidad radica en la limitación del espacio analítico correspondiente al problema de la gravitacion en cuatro dimensiones.
La mecanica analítica, libre de la supersticion del espacio-tiempo, resuelve el problema de forma clara y precisa al introducir el número necesario de variables.
La mecanica relativista patalea en el mismo lugar, incapaz de salir de su prision tetra dimensional.
El espacio analıtico tetra dimensional de Einstein no contiene los puntos analíticos 3n-dimensionales correspondientes a cada ubicacion de un conjunto de n partículas. Mientras que la relatividad solo puede tratar los elementos individualmente, la mecánica clasica trata el conjunto del universo observable en su totalidad.
Una vez mas, el libro prescinde de los procedimientos para llegar a la ecuacion (2). A pesar de esto, se puede apreciar que ambos numeradores corresponden a ecuaciones de Euler-Lagrange, que al ser iguales a cero pueden igualarse entre sí, al dividrse ambas entre un denominador comun, como hace el Dr. Le Roux. A partir de esto, el autor realiza varias suposiciones para llegar a la conclusion que la TR esta limitada por sus propias hipótesis.
Nuevamente, el espacio de configuraciones se presenta como el unico relevante y necesario. Las geodesicas pueden ser reparametrizadas, y el establecimiento de z4 = t + α corresponde a una parametrizacion afín, lo cual representa para el autor una ambiguedad.
Dado que Le Roux menciona en este punto el caso de dos soluciones que representan dos cuerpos arbitrarios, cabe mencionar que el problema de los 2 cuerpos no esta analíticamente resuelto en relatividad general. Contextualizando, el problema de un cuerpo en relatividad general consiste en resolver la dinamica de un objeto masivo que orbita alrededor de otro, lo suficientemente grande como para ser considerado en reposo. Así, por ejemplo, el perihelio de Mercurio se calcula dentro de esta aproximacion. Por otro lado, el problema de los dos cuerpos consiste en estudiar la dinamica de un genuino sistema binario (por ejemplo, dos estrellas de neutrones con masas comparables). La no lineali-dad de las ecuaciones de campo de Einstein y el hecho que el sistema binario produce ondas gravita-cionales (ausentes en la teorıa de Newton), hacen de este problema un desafío en cuanto a su resolucion analítica se refiere. No obstante, este hecho no favorece la afirmacion de Le Roux respecto a la incapacidad de la teoría relativista de dar cuenta de los fenomenos naturales; simplemente refleja la complejidad inherente de los mismos. El argumento es analogo a querer descalificar la teoría newtonia-na de la gravitacion por el simple hecho que el problema de los tres cuerpos no ha podido ser resuelto de forma analítica hasta la actualidad. Para una explicacion más rigurosa y detallada del problema de uno y dos cuerpos en relatividad general, recomiendo Damour (2013).
A pesar de esto, cualquier persona con conocimiento de la teoría de la relatividad que analice lo expuesto por el Dr. Le Roux desde una perspectiva matematica, debe otorgarle a este punto y a la publicacion de Le Roux (1933) especial atención.
Acotando la idea general del punto 7, en un libro muy referido en la pedagogía de la física, Fundamentals of Modern Physics, Robert Eisberg (1961) escribe lo siguiente:
"La teoría general de la relatividad que generaliza la teoría especial describiendo el movimiento en espacios-tiempos curvados, ademas engloba una teoría relativista de la gravitacion que generaliza la teorıa de gravitació de Newton."
Esta ultima frase está en total contradicción con la primera oracion y la idea general presentada en el punto 7. La teorıa de la relatividad cumple muy bien el denominado principio de correspondencia: Bajo ciertas condiciones, la teoría se corresponde al límite clasico. De este modo, la teoría de gravitacion de Newton prueba ser un caso específico de la teorıa relativista de gravitación. Actualmente, esto es demostrado y aceptado por la comunidad científica.
8. La fuerza de gravedad es una propiedad del universo observable, considerada en su totalidad. La gravitación se considera comunmente como la ley de aceleracion o interacción. De esta manera, sin embargo, es privada del problema de su verdadera naturaleza. El llamado efecto newtoniano, que es inversamente proporcional al cuadrado de la distancia, es valido solo para movimientos relacionados con ciertos sistemas de referencia. Como estos sistemas estan orientados hacia el cielo estrellado, en realidad dependen de la totalidad de las posiciones en el fondo observable de estrellas.
La redacción de la ley de atracción tambien presupone la elección de una característica especial para el tiempo, de modo que se pueda determinar la aceleración. Este tiempo canónico tambien se fija, teoricamente a través de la consideración del universo entero, practicamente mediante la aparente rotación del cielo estrellado. Siempre es la totalidad del universo lo que se valida.
El concepto de dos efectos remotos iguales y directamente opuestos parece en principio ser contrario a nuestro entendimiento. Sin embargo, demostramos que:
Cualquiera que sea el tipo de movimiento de un sistema de partıculas, siempre existen sistemas de referencia tales que el movimiento relativo de la totalidad de partículas en relación a cualquier partıcula, se debe unicamente a efectos mutuos, iguales y opuestos.
Las acciones recíprocas son, por lo tanto, esencialmente un hecho de la relatividad que resulta de la determinación de un sistema de referencia.
El método de Einstein no permitió descubrir este resultado significativo.
Para finalmente expresar la ley de acción mutua en una forma independiente de la elección de la variable de referencia, se tendría que usar todos los parámetros utilizados para determinar la posicion del universo total observable.
Esto también excede las posibilidades del metodo de Einstein. Los resultados confirmados por la escuela relativista parecen satisfactorios solo si se los admite sin crıticas. Esto es cierto, por ejemplo, para la afirmacion engañosa de 42'' para Mercurio en lugar de 374'' y la incapacidad del metodo para explicar esta diferencia.
Las observaciones presentadas en el primer parrafo de este punto parecen estar motivadas por el hecho que Einstein se esforzo durante varios anos en construir una teoría compatible con el principio de Mach, algo que nunca pudo concretarse.
Una discusion pormenorizada sobre el principio de Mach en la relatividad general esta fuera de los objetivos de este trabajo. Empero, dado que la cuestion sigue en discusión hoy día y existen opiniones diversas y divididas entre los expertos sobre este tema, sugiero acudir al texto Barbour & Pfister (1995) para mayores referencias.
Por otra parte, una de las consecuencias de caracter filosófico de la mecánica relativista es que elimina la accion a distancia. Como la información en la naturaleza es transmitida con una velocidad límite dada por la luz, se debe abandonar el concepto de simultaneidad presente, por ejemplo, en la mecanica newtoniana. Naturalmente, esto también se cumple en la interaccion gravitatoria. Un párrafo del capıtulo "¿Qué es el tiempo?" de La filosofía científica de Reichenbach (1951) senala lo siguiente:
"Vemos que la definicion causal de orden temporal conduce a una indeterminacion con respecto a la comparacion temporal de hechos ocurridos en puntos distantes. Y esto sucede así debido al caracter limitativo de la velocidad de la luz. El tiempo absoluto, es decir, la simultaneidad no ambigua, existiría en un mundo en el que no hubiera límite superior para la velocidad de las senales. Pero debido a que en nuestro mundo la velocidad de transmision causal es limitada, no existe absoluta simultaneidad. La teoría causal del tiempo explica el significado de la sucesion y la simultaneidad temporales en tal forma que la explicacion es aplicable tanto al mundo de la física clasica como a nuestro mundo, en el que la velocidad de la transmision causal se halla sujeta a un límite superior y la simultaneidad no es definida sin ambiguedad."
Acerca del concepto de tiempo estelar y las relaciones físicas dadas respecto al movimiento del cielo estrellado y la posicion del universo en su totalidad, es mi recomendacion personal acudir al excelente texto "The End of Time", escrito por Barbour (1999).
9. CONCLUSION. Estos hallazgos generales hacen que sea innecesario tratar varias irregularidades del método y las teorıas pseudo-geométricas de la relatividad. Uno gana la misma impresion con ellas y encuentra la misma falta de crıtica, combinada con algunas afirmaciones que significan verdaderos absurdos.
Mi conclusión muy clara es que la TR de Einstein no pertenece al campo de la ciencia positiva.
Debe entenderse que el autor usa la palabra "positiva" para referirse a aquella ciencia que es provechosa para la humanidad. No queda mucho que comentar sobre el punto 9. La conclusion del Dr. Le Roux es el texto perfecto para dar pie a las conclusiones de este trabajo.
3. CONCLUSIONES Y DISCUSION
Mientras algunos autores utilizan argumentos en contra de las implicaciones metafísicas, religiosas y filosoficas de la teoría de la relatividad, los puntos expuestos por el Dr. Le Roux se presentan de forma pretendidamente científica o academica, por lo que sus críticas son relevantes en comparacion a las anteriores. Es de destacar el aparato físico y matematico (siendo este último el preponderante) que da una base cientıfica común para refutar dichas críticas.
Los comentarios expuestos en este trabajo solo refieren puntos específicos de replica a los argumentos del Dr. Le Roux. Sin embargo, es relevante senalar algunas paradojas del texto, como que variados argumentos físico-matemáticos empleados eventualmente para desacreditar e invalidar la teoría de la relatividad, terminaron por validarla incrementando su credibilidad.
Por eso con el paso del tiempo, varios autores terminaron aceptando la teorıa de la relatividad. Aunque no es el caso de Le Roux, mi opinion refrenda la tesis de Kuhn que indica que una vez consolidado el paradigma, termina siendo aceptado por la comunidad científica, convirtiendose en la fuente de nuevas tematicas de investigación que refuerzan el nuevo paradigma.
Para apoyar esta tesis, acudo a un parrafo escrito en Fundamentals of Modern Physics, por Robert Eisberg (1961):
"La teoría de la relatividad fue disenada para estar de acuerdo con el hecho experimental que se observa que la velocidad de la luz es la misma en sistemas de referencia que tienen una traslacion uniforme con respecto al otro. Sin embargo, en adicion a esto, la teoría predice nuevos fenomenos tales como la contraccion de la longitud, la dilatación del tiempo, el aumento relativista de masa y una relacion entre la masa y la energía. Esto es típico de una teorıa científica. También es típico el hecho que la aceptacion inicial de la teoría fue solo tentativa, a pesar que parecía estar basada a partir de logica correcta. La teoría no alcanzo completo prestigio hasta que sus predicciones concernientes a nuevos fenomenos fueron puestas a prueba por experimentos."
Finalmente acudo al físico teorico alemán Hu-bert Goenner (1993), quien en su trabajo titulado The Reaction to Relativity Theory in Germany, III: "A Hundred Authors agaisnt Einstein" indaga extensamente en las motivaciones de los autores que aportan al libro, sus alegatos y publicaciones. Como el mismo afirma, su escrito se centra en responder las interrogantes de que motivó a los editores del libro, quienes fueron los que contribuyeron al mismo y cuales fueron sus problemas para entender la relatividad especial y general. No obstante, antes de dar cuenta de esto en el subtítulo titulado Einstein's Opponents, el Prof. Goenner escribe:
"Para mí, el libro es un ejemplo de una comedida pero inadecuada reaccion de la clase media en Alemania (Büdungsbügertum) a un topico en las ciencias exactas sin consecuencias economicas o tecnologicas inmediatas: la teoría de la relatividad. No existen muchos ejemplos de tal interaccion; en el siglo XIX, la teoría de la evolucion de Darwin sería uno; en nuestros tiempos, tal vez, la crisis en el fundamento de las matematicas, que se conoce a través de la sociedad en la forma de "nueva matematica". (...) Podemos ver claramente que tres temas estan ocultos detras de gran parte del pensamiento relativista en Hundert Autoren gegen Einstein: la disputa sobre la relacion entre 'realidad objetiva' y teoría física, la falta de conocimiento acerca de la manera por la cual el consentimiento publico entre los científicos para la validacion de una teoría cientıfica es establecida, y la cuestión de qué posible rol pueden jugar los no científicos en este proceso."
Los temas que senala objetivamente el Profesor Goenner atribuyen a la teoría de la relatividad, sin mayor reflexion, el carácter de revolución científica. Esto se evidencia ademas, en las características comunes con la teoría heliocentrica de Copérnico y la teoría de la evolucion de Darwin: dos revoluciones científicas por excelencia, segun Thomas Kuhn.
Queda abierto para los hispanohablantes conocedores de la teoría de relatividad, el ejercicio de analizar profundamente los argumentos del Dr. Le Roux, formulando juicios científicos y de valor sobre los mismos, en mi opinion, orientándolos a restar credito al matemático francés. Finalmente, invito a los lectores curiosos germano-parlantes, a leer la obra Hundert Autoren gegen Einstein, para consolidar y aun eventualmente discutir, en torno a la epistemología de los paradigmas de Thomas Kuhn y la teoría de la revolucion científica generada por la teorıa de la relatividad, criticando los fundamentos de quienes se opusieron a la brillante teoría de Albert Einsetin.
AGRADECIMIENTOS
El presente artículo surgio como una extensión del trabajo final de la materia Historia de la Ciencia, dada en la carrera de física, UMSA en el periodo I/2018. Agradezco a quien impartio la materia: Diego Sanjines Castedo, Ph.D. por darme a conocer la existencia del libro, sugerirme y orientar el tema. Ademas, por sus recomendaciones, correcciones e invaluable ayuda con la edicion del mismo. Tambien agradezco a Zui Oporto-Almaraz, Ph.D. por las valiosas reuniones y la bibliografía proporcionada. Sus comentarios, correciones y aportes al trabajo permitieron pulir y dar forma final al texto.
Conflicto de intereses
El autor declara que no hay conflicto de intereses con respecto a la publicacion de éste documento.
NOTAS
1 El texto en alemán abrevia “teoría de la relatividad” como RTH. El presente artículo señala TR.
2 Aquí solo se hace alusión a la ecuación usada para calcular la precesion.
3 En el texto se denota cualquier variable con negrilla (n). En la traducción, yo uso itálicas para evitar la confusión con variables vectoriales.
REFERENCIAS
Álvarez-Gaumé, L. & Vázquez-Mozo, M. (2005). Einstein y la Geometría, CERN-PH-TH, 034, 05. [ Links ]
Barbour, J. (1999). The End of Time: The Next Revolution on Physics. Oxford University Press. ISBN 13 978-0-19-511729-5. [ Links ]
Barbour, J. & Pfister, J. (1995). Mach's Principle: From Newton's Bucket to Quantum Gravity. Birkhauser Boston. ISBN 0-8176-3823-7. [ Links ]
Clifford, W. (2014). Was Einstein Right? A Centenary Assessment. A publicarse en: General Relativity and Gravitation: A Centennial Perspective. arXiv: 1409.7871 [gr-qc]. [ Links ]
Clifford, W. (2014). The Confrontation between General Relativity and Experiment. Living Reviews in Relativity, 17, 4. [ Links ]
Damour, T. (2013). The general relativistic two body problem, en Brumberg Festschrift, Berlin. Editado por S. M. Kopeikin. arXiv:1312.3505 [gr-gc]. [ Links ]
Eddy, H., Morley, E. & Miller, C. (1898). The Velocity of Light in the Magnetic Field. Physical Review, 5, 283-295. [ Links ]
Eisberg R. (1961). Fundamentals of Modern Physics, 3a edicion. Ed. John Wiley and Sons. CCN 61-6770. [ Links ]
Ernst, A. & Hsu, J. (2001). First proposal of the universal speed of light by Voigt in 1887. Chinese Journal of Physics, 39, 3. [ Links ]
Goenner, H. (1993). The Reaction to Relativity Theory I: The Anti-Einstein Campaign in Germany in 1920. Science in Context, 6(1), 107-133. doi:10.1017/S0269889700001332 [ Links ]
Holton, G. (1969). Einstein and the "Crucial" Experiment. American Journal of Physics, 37, 10. [ Links ]
Israel, H., Ruckhaber, E. & Wienman, R. (1931). Hundert Autoren gegen Einstein. VoigtlánderS Verlag. CDB 94197100. [ Links ]
Jourdain, P. (1912). The Principle of Least Action. Remarks on some Passages in Mach's Mechanics. Source: The Monist, 22, 2, 285-304. [ Links ]
Kittel, C. (1971). Larmor and the Prehistory of the Lorentz Transformation. American Journal of Physics, 42, 726-729. [ Links ]
Le Roux, J. (1933). Le principe de relativite et la loi de la gravitation. Annales Scientifiques de L'E.N.S., 50, 3. 127-169. [ Links ]
Nomizu, K. (1996). Foundations of Differential Geometry. Ed. Wiley-Interscience. CCN 63-19209. [ Links ]
O'Connor, J. & Robertson, E. (1996). Special Relativity. His-tory Topics, Mathematical Physics. School of Mathematics and Statistics, University of St Andrews, Scotland. Web. 2 de febrero de 2020. [ Links ]
Pauli, W. (1958). Theory of Relativity, Dover Publications. ISBN 0-486-64152-X. [ Links ]
Reichenbach, H. (1951). La Filosofía Científica. Berkeley, California. Segunda edicion en español, traducido por Horacio Flores Sanchez. Fondo de cultura de México. [ Links ]
Stokes, G. (1845). On the aberration of light. The London, Edin-burgh and Dublin Philosophical Magazine and Journal of Science, 27, 177, 9-15. [ Links ]
Wiki: Jean-Marie Le Roux. En Wikipedia. Recuperado el 12 de febrero de 2020. https://en.wikipedia.org/wiki /Jean-Marie-Le-Roux