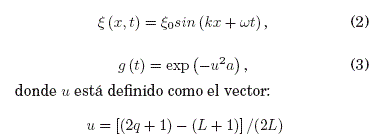Services on Demand
Journal
Article
Indicators
Related links
Share
Revista Boliviana de Física
On-line version ISSN 1562-3823
Revista Boliviana de Física vol.34 no.34 La Paz Nov. 2019
A. ARTÍCULOS
Análisis multi-resolución (AMR) en el dominio K-X, aplicaciones a sísmica 3D-2D
caso: Subandino Centro de Bolivia
Multiresolution analysis in the K-X domain, 3D-2D seismic applications in the
Central Bolivian Subandean zone
Evanz Lázaro† & Kim Bejarano‡
† YPFB Chaco S.A.
lazaro.evanzv@gmail.com
‡ Universite Toulouse III Paul Sabatier
geokim7@gmail.com
(Publicado con la autorización de la Université Toulouse III Paul Sabatier)
Resumen
Se muestra la aplicacion de la técnica Análisis Multi-Resolución (AMR) en el espacio k x (numero de onda-espacio) a los datos sísmicos 3D de un campo productor de gas en el subandino central de Bolivia. Geológicamente la investigación se centra en estudios profundos alrededor de los 4200 m (TVD), sobre la formacion Robore (arenas ArRob I, II y III) en niveles del Devonico Inferior (390 MA). Los resultados, denominados anomalías-k, muestran una interesante relacion entre longitudes de onda larga y estructuras geológicas contenedoras de hidrocarburos. Para dar certeza a los resultados se han correlacionado con registros gamma ray (GR) y densidad neutron de pozo, mostrando gran coherencia entre anomalías-k y la ubicacion en profundidad de los reservorios de hidrocarburos. Adicionalmente los resultados son comparados con atributos sísmicos extraídos desde una PSDM, y extraídos desde un cubo 3D de anomalías-k, mostrando mejor resolucion en el último caso.
Codigo(s) PACS: 93.85.Rt - 02.30.Nw - 91.25.Ga
Descriptores: Metodos sísmicos - análisis de Fourier - Variaciones espaciales: todos los armonicos y anomalías
Abstract
The Multiresolution Analysis (AMR) technique is applied in the k x domain (wave num-ber - space) to 3D seismic data of the gas producer field in the central Bolivian sub-andean zone. Geológically the research is focused on deep studies around 4200 m (TVD), on the Robore sands (ArRob I, II and III) at levels of the Lower Devonian (390 MA). The results, called k-anomalies, show an interesting relationship between long wavelengths and geológical structures containing hydrocarbons. To give certainty to the results, these anomalies have been correlated with well-log gamma ray (GR) records, showing great coherence between k-anomalies and the deep location of hydrocarbon reservoirs. Additionally, the results are compared with seismic attributes extracted from a PSDM seismic and extracted from a 3D cube of k-anomalies, showing better resolution in the latter case.
Subject headings: Seismic methods - Fourier analysis - Spatial variations: all harmonics and anomalies
1. INTRODUCCION
El origen de la tecnica de Análisis Multi-Resolucion (AMR) se remonta a los anos 90 del siglo pasado en la ingeniera electrica, donde la preocupacion principal era identificar pulsos parasitos (ruido) acoplados en transmisiones electricas. Valiéndose de análisis espectral mediante transformadas de Fourier en ventanas de tiempo menores a la longitud de una senal, logran caracterizar espectralmente estos pulsos, localizar su posicion en tiempo y de esa manera, disenar filtros para aislarlos. En el campo de exploracion y desarrollo de hidrocarburos, no es habitual encontrar estudios de análisis espectrales aplicados a datos sísmicos; por lo general, los estudios se enfocan en la interpretación de amplitudes sísmicas correlacionados con modelos geológicos. Es posible citar algúnos pocos trabajos de análisis espectrales tales como el ISA (análisis espectral instantaneo, por sus siglas en ingles) desarrollado por Huang et al. (1998), Transformadas Wavelet CWT explicadas por Daubechies (1992), la transformada S expuesta por Stockwell et al. (1996) y recientes como la descomposicion empírica completa en modos por conjuntos (CEEMD por su sigla en ingles), utilizada por Han & van der Baan (2012), que tienen en comun el concepto de descomposicion espectral de secciónes sísmicas, con el obje-
tivo de estudiar el vínculo entre frecuencias bajas y estructuras con presencia de hidrocarburos como lo senalan Odebeatu et al. (2006). En este marco conceptual el presente trabajo viene a ser de algúna manera una aplicacion del proceso de Descomposición Espectral.
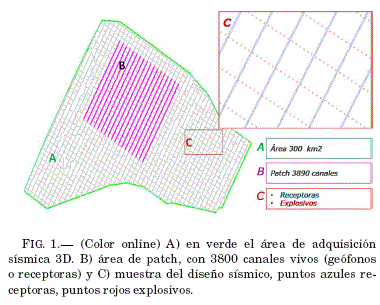
En 2012 con fines de exploracion y desarrollo de hidrocarburos, se llevo a cabo una campaña de adquisicion sísmica 3D sobre un campo productor de gas en pie de monte del subandino centro de Bo-livia. El diseno sísmico para esta campana fue de tipo Regular como se muestra en la Fig. 1; es decir, un diseno ortogonal entre línea de receptoras (geofonos o canales-InLine) y línea de explosivos (shot-XLine). Con un espaciado entre receptoras de 40 m (puntos azules) y 80 entre puntos explosivos (puntos rojos), con separacion entre InLine de 480 m igual que para XLine y con un fold nominal de 80 (puede entenderse como repetitividad de trazas en un mismo punto reflector en subsuelo).
En general los datos sısmicos 3D obtenidos de esta campana fueron de muy buena calidad. Posteriormente, estos datos se procesaron en ambos dominios: tiempo (PSTM- pre stack time migration) y en profundidad (PSDM- pre stack depth migration ) mediante el algoritmo Kirchhoff (ver Fig. 2). Durante el procesamiento de datos sısmicos se dio énfasis en mantener, en lo posible, las características de las trazas sísmicas; es decir, al menos tener un procesamiento con preservacion de amplitudes sísmicas consistentes con superficie y recuperacion de frecuencias por deconvolucion.
A pesar de la variedad y riqueza de informacion que contiene una descomposicion espectral de secciónes sísmicas, no es muy comun que los intérpretes geofísicos o geológos la utilicen durante la interpretación y generación de prospectos o modelos estructurales; esto por diferentes razones, una de ellas podría ser que no se cuenta con una plataforma informatica que esté al alcance de todos.
2. ANÁLISIS MULTI-RESOLUCIÓN (AMR) MEDIANTE TRASNFORMADA RAPIDA DE FOURIER
El análisis multi-resolución (AMR) consiste en estudiar las condiciones no estacionarias de una señal o serie de tiempo, a través del análisis espectral aplicado por ventanas temporales a lo largo de una senal. Matemáticamente el análisis AMR demanda un operador de transformacion, que podría ser algo sofisticado como transformadas wavelets o algo mas simple como una transformada de Fourier. Evidentemente, la condicion de no estacionaria de una onda esta reflejada en su dependencia funcional de la frecuencia ω respecto de la posición x, tiempo t y velocidad v, esta dependencia puede ser aprovechada para identificar y asociar fases específicas de la onda con las propiedades físicas del medio de propagacion.
![]()
En el caso especifico de ondas sısmicas, durante su propagacion y al margen de los procesos de pérdida de amplitud por decaimiento, propagacion y otros factores, los cambios de amplitud estan asociados generalmente a cambios de densidad y si ademas existe un cambio en las frecuencias se atribuye a variaciones de velocidad del medio de propagacion de la onda sísmica. Estos dos aspectos, cambio de amplitud y frecuencia, define geofísicamente el caso de un medio anisotropico, que en términos estructurales implicaría presencia de cuerpos anomalos. El análisis espectral de señales sísmicas, puede ser abordado en dos dominios: tiempo-frecuencia o espacio-numero de onda, dependiendo si la sísmica esta procesada en tiempo PSTM o profundidad PSDM respectivamente.
3. DESCRIPCION DE LA METODOLOGÍA (AMR)
Para entender la metodología de manera didactica, considere como senal de estudio una traza sintética, cuya forma caracterizada por la frecuencia ω y numero de onda k esta descrita en la Ec. (2), una
funcion ventana tipo gauss dada por la Ec. (3) y un proceso de deconvolucion entre ambas funciones.
con q = 1,2,...,L , L es la longitud y ![]() es el ancho, de la funcion ventana expresado en muestras. Este ultimo estadísticamente representa la desviacion estandar del valor más probable en una distribución de gauss.
es el ancho, de la funcion ventana expresado en muestras. Este ultimo estadísticamente representa la desviacion estandar del valor más probable en una distribución de gauss.
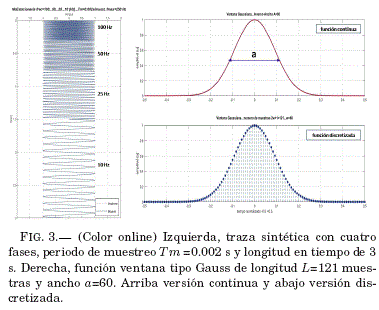
Definamos el caracter de la traza sintética como no estacionaria, con cuatro fases de 100 Hz, 50 Hz, 25 Hz y 10 Hz, con un periodo de muestreo de 0.002 s y una longitud total de 3 s. Fig. 3. La funcion ventana tipo gauss esta definida por los parámetros, longitud de 121 muestras y un ancho de 60 muestras Fig. 3.
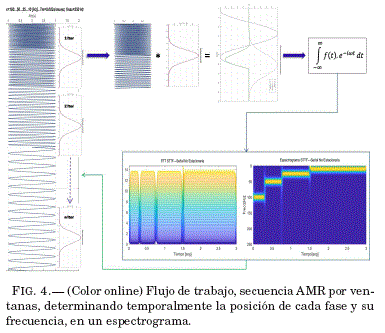
Ambas funciones, traza sintetica y ventana gaus-siana, son sometidos a un operador de convolucion e inmediatamente se determina el contenido espectral, de la ventada resultante, mediante una transformada rapida de Fourier STF ( Short-time Fourier Transform). Se establece una secuencia iterativa, desplazando la ventada gaussiana en pasos de ![]() /2 muestras a lo largo de la traza sintetica, realizando en total n-iteraciones hasta cubrir la totalidad de la longitud de la traza. El resultado espectral de cada iteracion será integrada en un único espectrograma Fig. 4.
/2 muestras a lo largo de la traza sintetica, realizando en total n-iteraciones hasta cubrir la totalidad de la longitud de la traza. El resultado espectral de cada iteracion será integrada en un único espectrograma Fig. 4.
En efecto, debido a la posibilidad de elegir diferentes parametros de la función ventana, cada conjunto de parametros seleccionados, enfatizará con mayor precision o la frecuencia o la posición temporal de cada fase, pero no ambos, un analogo al principio de incertidumbre de Heisenberg aplicado a ondas sısmicas, tal como se muestra en la Fig. 4 (parte inferior, los dos espectrogramas), donde se puede apreciar la resolucion en posición temporal (abscisas) o la definicion de frecuencia de las fases (ordenadas)
todo en el espacio ![]() (frecuencia-tiempo). Ahora bien, si es posible descomponer espectralmente la traza sintetica en sus cuatro fases, entonces es posible separar una fase en particular del resto, de hecho esta sera parte fundamental de la técnica para la generacion de espectrogramas en las siguientes secciónes.
(frecuencia-tiempo). Ahora bien, si es posible descomponer espectralmente la traza sintetica en sus cuatro fases, entonces es posible separar una fase en particular del resto, de hecho esta sera parte fundamental de la técnica para la generacion de espectrogramas en las siguientes secciónes.
4. APLICACION POST-PROCESO DE LA METODOLOGÍA (AMR) A SISMICA 3D
4.1. Geología y Estratigrafía del área de estudio
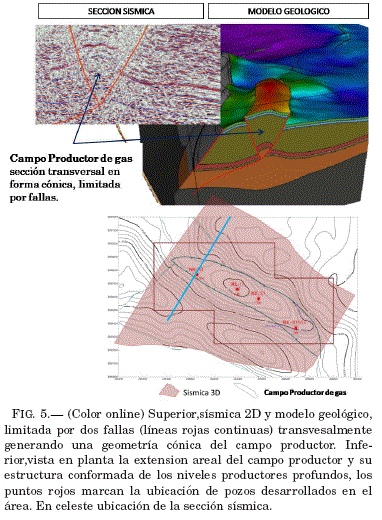
El área en cuestión es un campo productor de gas descubierto preliminarmente con sísmica 2D y desarrollado en produccion con sísmica 3D. La forma geometrica del campo productor, está definida dos fallas (líneas continuas rojas en la sección sísmica) y levantado verticalmente por esfuerzos tectonicos, formando una especie de cono. Este campo presenta dos niveles de produccion de hidrocarburos, uno de niveles someros como las formaciones Yantata y Cajones del sistema Cretácico y otro de niveles profundos vinculado a formaciones del Devonico Inferior, denominadas Arenas Robore (ArRob I, II y III) Fig. 5.
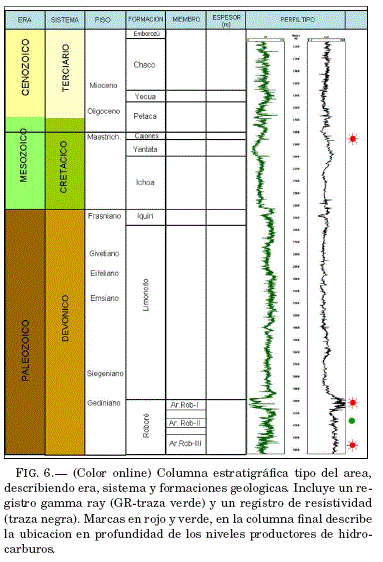
En la Fig. 6 se muestra la columna estratigrafica tipo del area de estudio y se destacan los niveles de produccion de hidrocarburos con marcas en rojo para gas y verde para petroleo. Este trabajo esta enfocado unicamente a los reservorios profundos.
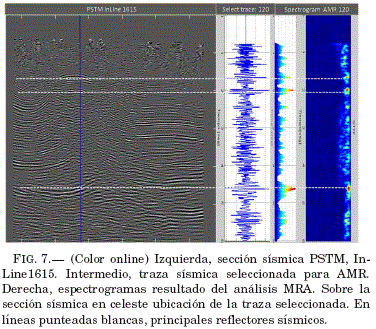
4.2. Análisis Multiresolución en tiempo PSTM
Consideremos el cubo sísmico 3D migrado en tiempo PSTM (pre stack time migration) de donde se toma la sección sísmica InLine 1615, lınea celeste en el mapa Fig. 5. Se considera ahora una traza sismica real, extraida de la sección sísmica, línea azul en la figura (fig.7), a la cual se aplica la metodología AMR. La traza sísmica seleccionada es de 6 segundos de longitud, esta muestreada a razon de 2 ms lo que implica una recuperacion de fases teóricamente hasta 250 Hz (Teorema de Nyquist). Consideremos ademas la necesidad de obtener fases sísmicas con una mayor
resolucion temporal que una resolución en frecuencia (Barnes, 2007; Han and van der Baan, 2011), esto implica un proceso de seleccion por comparación cualitativa entre diferentes parametros de la función ventana. En este caso se selecciona una funcion ventana tipo Gauss de longitud 60 y un ancho de 30 muestras, el criterio de esta seleccion esta fundamentada en aspectos geológicos como se mostrara mas adelante.
Queda claro que cada traza de la sección sísmica genera un espectrograma, entonces se genera un cubo espectral por cada sección sísmica. En el lenguaje del algebra lineal, una traza sísmica representa un vector, el espectrograma de una unica traza es una matriz, el espectrograma de una sección sísmica representa una hipermatriz y el espectrograma de todo un cubo sısmico 3D representa un hipercubo. Como referencia para efectos de informaticos, el cubo sísmico 3D contiene del orden de 10e4 trazas, cada traza se descompone en 250 frecuencias y cada traza ademas tiene del orden de 10e3 muestras, por lo que la cantidad de datos que compone el hipercubo es del orden de 10times1010. Esto implica un manejo muy grande de datos y mucha exigencia informatica, razón por la cual es necesario acotar intervalos de frecuencias y decimar los pasos de frecuencia.
4.3. Análisis Multiresolución en profundidad PSDM
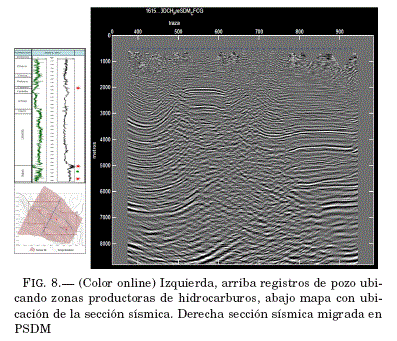
Se considera la misma sección sísmica InLine1615, pero esta vez del cubo sısmico 3D con proceso de mi-
gracion PSDM. Esta sección corta transversalmente al campo productor y pasa exactamente por un pozo productor de gas de los niveles profundos, Fig. 8.
Nuevamente se aplica la secuencia AMR traza por traza a toda la sección sísmica PSDM, con la diferencia que ahora se trabaja en el dominio k x (numero de onda-espacio) puesto que la sección sísmica se encuentra migrada en profundidad. La construcción de
los espectrogramas ahora se hace solo para determinados valores de k, Fig. 9
El criterio de seleccion de valores de k, debe estar ligado al sentido geológico, algúno de estos pueden ser espesores de las diferentes formaciones geológicas, estratigrafía definida por registros de pozo, condiciones geotectonicas y estructurales del medio, entre otros. Longitudes de onda fuera de este rango posiblemente no tendrían sentido geológico. En la Fig. 10, se visualiza el impacto de la seleccion de diferentes valores de k, mostrando cada sección espectral detalles del subsuelo diferentes para cada longitud de onda. Es evidente que longitudes de onda larga detallan mejor aspectos profundos del subsuelo, mientras que longitudes de onda corta son mas apropiadas para eventos someros.
4.4. Anomalías-k y Registros de Pozo
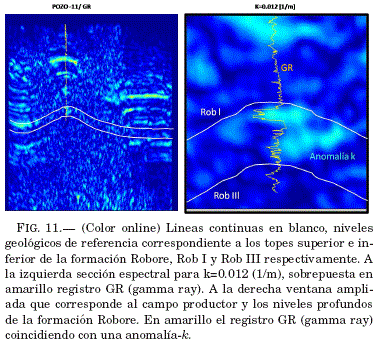
Ahora es posible separar secciónes espectrales para determinadas longitudes de onda o numero de onda k que sean de algún interés en particular. Por ejemplo el numero de onda k = 0.012 (1/m) presenta una empatıa muy alta con el registro gamma ray (GR) y el registro de resistividad, que claramente identifican las arenas de Robore (ArRob I,II y III) productoras de hidrocarburos y la anomalia espectral posicionada a la misma profundidad proveniente del análisis AMR, a estas coincidencias de valores espectrales, se denominan anomalías-k. Fig. 11. Puede entonces inferirse que para este valor de k y a profundidades alrededor de los 4200 m (TVD-true vertical depth), las areniscas ArRob I-III pueden ser identificadas y mapeadas como anomalías-k, a lo largo de todo el campo.
5. ATRIBUTOS SISMICOS VS ANOMALIAS-K
Es menester que los resultados obtenidos sean sometidos a comparación con el fin de validar y apreciar los beneficios a obtener o incluso las mejoras por realizar. La identificacion y el mapeo de anomalías-k en todo el cubo espectral requiere de una base de datos (geológico-geofísico) y con el proposito de realizar comparaciones con atributos sısmicos realizado con otros algoritmos, se exportan los resultados espectrales a un software comercial y especializado en visualizacion de imágenes sísmicas, interpretación geológica y extracción atributos sísmicos. En esta plataforma comercial, se muestran las secciónes espectrales y anomalías-k; (manchas amorfas naranja claro)que atraviesan pozos profundos con registros GR (en rojo), Fig. 12. Para este proposito se consideran los registros GR de seis pozos profundos denominados POZO-X3, POZO-8, POZO-10, POZO-11, POZO-9DST y POZO-12ST productores de hidrocarburos en los niveles profundos.
Un caso interesante es el del POZO-12ST. Inicial-mente se programo como un pozo vertical con un pequeno desvío (línea continua naranja en el grafico). Durante la perforacion el equipo sufre un problema de entrampamiento de herramienta (pesca), por lo que se decide realizar un sidetrack (desviar la dirección de perforación del pozo) en dirección de los mejores indicios de detección de hidrocarburos resultando un pozo exitoso, que coincide plenamente con las anomalías-k;.
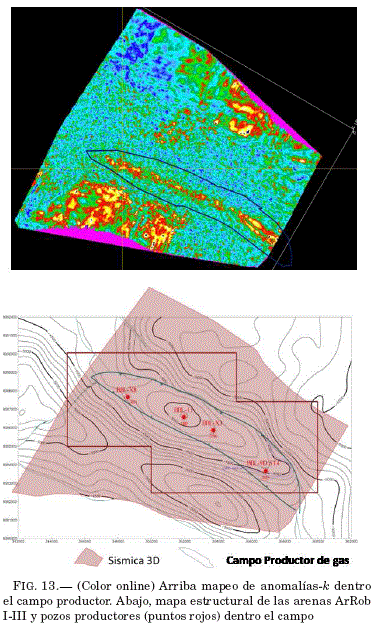
Para el mapeo de anomalías-k; en el cubo espectral, se considera una ventana de aproximadamente 250 m de espesor utilizando como tope alto el horizonte sısmica Rob l y como base el horizonte sísmico Rob lll ( Fig. 11). Haciendo una extraccion de anomalías-k, entre estos horizontes obtenemos un corte variable en profundad visto como un plano en la Fig. 13. El campo productor de hidrocarburos esta enmarcado en línea oscura y es de destacar, que de acuerdo al mapeo geológico, la distribución de las arenas Robore
l-III, zonas de concentracion de hidrocarburos con muy alta probabilidad de certeza (verificado con los pozos productores), coincidentes con la concentracion de anomalías-k.
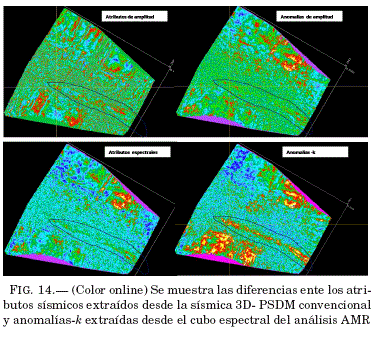
Sobre el mismo campo y entre los mismos horizontes Rob-l y Rob-lll, se realiza un análisis de atributos sísmicos, basados en extraccion de amplitudes y espectros, pero sobre el cubo 3D PSDM convencional. En la Fig. 14, se muestran las diferencias entre atributos sísmicos, anomalías de amplitud y las anomalías-k, como era de esperar, las anomalías-A; caracterizan con mayor resolucion la distribución de las arenas productoras ArRob I-II-III a lo largo de todo el campo.
6. OTRAS APLICACIONES- GEOCUERPOS E INTERPRETACIÓN ESTRUCTURAL
Otra aplicacion de las anomalías-k, con la premisa de que estas reflejan propiedades petrofísicas del medio de propagacion de ondas sísmicas, tal como la de saturacion de fluidos, es construir Geocuer-pos celulares. Considerando nuevamente el paquete sísmico entre los horizontes Rob-l y Rob lll. se define el llenado de todas las anomalías espectrales con microcelulas de forma esférica a través de algorit-
mos estadísticos que permiten minimizar los espacios vacıos entre esferas. En la Fig. 15 se muestra la imagen de lo que serıa probablemente la más realista de la forma de distribución de hidrocarburos para los niveles profundos del campo productor.
Una de las potenciales utilidades del análisis mul-tiresolucion es la generación de imágenes en el espacio ![]() durante una interpretación estructural, reduciendo ruidos de migracion, difracciones y definiendo limites no visibles en la imagen sísmica convencional.
durante una interpretación estructural, reduciendo ruidos de migracion, difracciones y definiendo limites no visibles en la imagen sísmica convencional.
Se ha aplicado el análisis AMR a sísmica 2D PSTM antigua. Seleccionando bajas frecuencias, se llega a
observar el nivel del basamento y se logra definir las formaciones principales que en sísmica PSTM no es tan simple de distinguir. Figura 17 En esta ultima imagen se puede observar claramente los horizontes guıa como son las formaciones Yantata y Roboré a lo largo de la línea sísmica. Se pueden observar dos eventos claros en esta imagen:
1. La frecuencia en la zona de la Fm El Carmen (Ver Fig. 17), por debajo de la Formacion Robore, más concretamente las rocas del Silúrico.
2. El límite de la formacion Yantata en la zona central norte (Ver Fig. 17).
Estos dos tramos muestran la misma resolucion, posiblemente generada por los esfuerzos del contacto entre la roca y la falla adyacente, ya que si se observan estos puntos variando las frecuencias, se mantendran con mucha resolución.
Se hace hincapie en este evento, ya que se presenta en el area de imagen pobre generando incertidum-bre, por lo que serıa una confirmación de la presencia de esfuerzos compresivos.
Estos horizontes son muy coherentes con los de la sísmica, llegando a definir de mejor forma cualquier interrupcion en cuanto a litología, incluso llegando a definir pendientes abruptas.
7. CONCLUSIONES
La metodología de análisis Multiresolución AMR, muestra la riqueza de información contenida en los análisis espectrales de datos sísmicos. Esta metodología funciona independientemente de la disponibilidad de otros datos geofísicos; sin embargo, con mayor certeza si existen registros de pozos; específicamente para la determinación de los números de onda k coherente con el sentido geológico. Bajo estas condiciones:
1. Se muestra una buena correlacion de las anomalías k, con niveles arenosos productores de hidrocarburos.
2. Acompañado de un buen análisis petrofísico, podría utilizarse para determinacion de volumenes mediante la generación de geocuer-pos y para estudios de caracterizacion de reservorios.
3. La extraccion de atributos sísmicos son de mayor resolucion sobre cubos espectrales 3D construidos con AMR que sobre simples cubos 3D de amplitud PSTM/PSDM.
4. Ayuda en procesos de interpretación estructural e identificacion de discontinuidades, reflectores sísmicos eliminando ruidos de sub o sobre migracion o difracciones en general.
Adicionalmente a este trabajo, se ha generado una plataforma JAVA interactiva, con algoritmos escritos en C++ y librerias de MatLab, que permite trabajar los datos sımicos desde el cargado SGY hasta la generacion de cubos espectrales tanto en el espacio f t para PSTM como en el espacio k x para PSDM, es decir se trata de una aplicacion postproceso, disponible con permiso de los autores.
AGRADECIMIENTOS
Agradecemos a la gerencia de YPFB CHACO S.A., a la Universite Toulouse III Paul Sabatier por cooperar con esta investigacion y al Dr. Patrice Baby por la transmision de conocimientos en aspectos estructurales.
Conflicto de intereses
Los autores declaran que no hay conflicto de intereses con respecto a la publicación de éste documento.
REFERENCIAS
Huang, N.E., Shen, Z., Long, S.R., Wu, M.C., Shih, H.H., Zheng, Q., Yen, N.C., Tung, C.C. & Liu, H.H. (1998), Proceedings ofthe Roy al Society of London, Series A: Mathematical,Physical and Engineering Sciences 454, 903-995. [ Links ]
Daubechies, I. (1992), Ten Lectures on Wavelets (Pennsylvania: The Society for Industrial and Applied Mathematics). [ Links ]
Stockwell, R.G., Mansinha, L. & Lowe, R.P. (1996), IEEE Trans-actions on Signal Processing 44, 998-1001. [ Links ]
Han, J. & van der Baan, M. (2012), Complete Ensemble Empiri-cal Mode Decomposition for Seismic Time-Frequency Analysis, University of Alberta, SEG Las Vegas 2012 Annual Meeting. [ Links ]
Odebeatu, E., Zhang, J., Chapman, M., Liu, E. & Li, X. (2006), The Leading Edge 25(2), 206-210. [ Links ]