A.ARTÍCULOS

 

Sincronización de tríos de neuronas de Rulkov caracterizadas
por periodicidades

 

Periodicity characterized synchronization of a trio of
Rulkov neurons

 

 

Kevin Iglesias^* & Gonzalo Marcelo Ramírez-Ávila^**
* Instituto de Investigaciones Físicas, Universidad Mayor de San Andres c. 27 Cota-Cota, Campus Universitario,
Casilla de Correos 8635 La Paz-Bolivia kcordero@fiumsa.edu.bo
^** Instituto de Investigaciones Físicas, Universidad Mayor de San Andres c. 27 Cota-Cota, Campus Universitario,
Casilla de Correos 8635 La Paz-Bolivia http://www.fiumsa.edu.bo/docentes/mramirez/
Recibido: 2 de julio de 2019    aceptado: 10 de agosto de 2019

 

 

---

Resumen

Se estudia la sincronizacion en función a la intensidad de acoplamiento de tríos de neuronas de Rulkov caracterizadas por periodicidades y electricamente acopladas bidirec-cionalmente. Primeramente, se determino el comportamiento dinámico de una neurona de Rulkov caracterizandolo mediante periodicidades en el plano de parámetros; donde se tiene regiones en las que se producen rafagas de picos típicas de estos sistemas. Se obtuvieron cuencas de atraccion del modelo de Rulkov, para las cuales se observó multiestabilidad. Se trabajo tanto con neuronas idénticas como diferentes pero con la misma periodicidad. Se encontro que la configuración heterogénea facilita la sincronización, lo cual se comprobó mediante el analisis de las series temporales de la variable lenta.

Codigo(s) PACS: 05.45.-a-87.19.ll-05.45.Xt

Descriptores: Dinamica no lineal y caos - Modelos neuronales - Sincronización; osciladores acoplados

---

Abstract

We studied synchronization as a function of coupling strength in a trio of Rulkov neurons characterised by their periodicities, and considering electrically and bidirectional coupling. Firstly, we determined the dynamical behavior of a single neuron by using its periodicities in the parameter plane. We identified the typical behavior of spiking-bursting in several regions of this plane. Several basins of attraction for the Rulkov model were obtained exhibiting multistability. We worked with identical and different neurons but with the same periodicity. We found that the heterogeneous configuration enhances synchronization an aspect that was verified by analyzing the time series of the slow variable.

Subject headings: Nonlinear dynamics and chaos - Neuron models - Synchronization; coupled oscillators

---

 

 

1. INTRODUCCIÓN

El estudio de muchos sistemas dinámicos conduce a ecuaciones diferenciales y/o mapas (sistemas discretos), que generalmente presentan un comportamiento no lineal y no poseen solución analítica. El área que trata dichos sistemas es la dinámica no lineal, estudiada ampliamente (ver por ejemplo los cursos introductorios de Strogatz (1994) y Nicolis (1995)). Para el estudio de sistemas no lineales, usualmente se recurre a un análisis de estabilidad lineal complementado por otro de bifurcación. La solución de este tipo de sistemas, generalmente es obtenida de manera numérica.

La neurociencia es el estudio de cómo se desarrolla el sistema nervioso, su estructura y su funcionalidad, como lo señala Wickens (1995). La parte más importante del sistema nervioso es el cerebro; en particular, el cerebro humano es uno de los sistemas más difíciles de analizar, debido a la gran cantidad de constituyentes (neuronas) que según Longstaff (2011) tiene un estimado de 8.6 × 1010 neuronas y cada una de ellas con aproximadamente 104 conexiones.

Para utilizar las ideas de la dinámica no lineal en neurobiología, se presenta al sistema nervioso como un sistema de entrada/salida de información; es decir, el sistema nervioso interactúa con su entorno mediante ráfagas de picos para transportar la información a través de circuitos neuronales como lo muestran Abarbanel & Rabinovich (2001). La informacion es procesada y distribuida para producir una respuesta relacionada a una actividad funcional específica del cerebro. Desde el punto de vista fisiologico, el papel principal lo tiene la membrana lipídica, donde se tienen cambios abruptos de potencial, lo cual genera una rafaga de picos eléctricos o potenciales de accion que son transportados por el axon; siendo este comportamiento explicado por Izhikevich (2007).

El estudio de la interaccion de neuronas en una red ha dado lugar al surgimiento de nuevas disciplinas, como por ejemplo, la neurociencia computacional que incluye tecnicas matemáticas sofisticadas para resolver ecuaciones diferenciales y sistemas dinamicos en general, como lo hacen Borisyuk et al. (2005).

Existen distintos tipos de neurona con sus respectivos modelos. A grandes rasgos, Abarbanel et al. (1999) definen a la neurona como un sistema que no esta en equilibrio y que además posee varios mecanismos de retroalimentacion y retardo; los cuales, proporcionan a la neurona un carácter oscilatorio. El primer modelo de neurona fue propuesto por Hodgkin & Huxley (1952) después de realizar una serie de trabajos experimentales con neuronas de calamar gigante; en tanto que Lamberti & Rodríguez (2007) proporcionan una deduccion matemática de dicho modelo.

Posteriormente, se postularon diversos modelos neuronales mas simples con la característica principal de ser descritos por ecuaciones diferenciales no lineales, por lo que, obtener una solución analítica es muy difícil. Es así que se recurre al calculo numérico.

En este trabajo se muestra el estudio de la sincronizacion para las dos posibles configuraciones de tríos de neuronas de Rulkov tanto diferentes como identicas en sus parámetros intrínsecos, caracterizando a cada neurona por su periodicidad. En la Sec. 2 se explica el modelo utilizado y se caracteriza al mismo por sus periodicidades; en tanto que los detalles de la sincronizacion para los sistemas mencionados se dan en la Sec. 3. Los resultados que conducen a la determinacion de multiestabilidad y a la descripcion de la sincronización a través del error medio se exponen en la Sec. 4. Finalmente, se dan las conclusiones y perspectivas de este trabajo.

 

2. MODELO DE NEURONA DE RULKOV

Una version simplificada de modelo de neurona es planteada por Rulkov (2001), cuya formulacion consiste en dos ecuaciones en diferencias, lo que es conocido como mapa de Rulkov. Por lo tanto, se tienen dos variables dinamicas acopladas que reproducen los comportamientos neuronales mas importantes como ser: oscilaciones sostenidas, situaciones de estacionariedad (punto fijo) y rafagas de picos o "bursts of spikes" seguidos por episodios de estacionariedad o silencio. Las ecuaciones del modelo son:

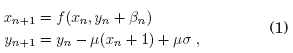
donde

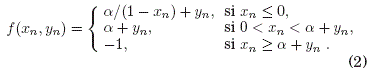
Siendo x y y las variables dinamicas rápida y lenta respectivamente. Los parametros μ,α y σ estan asociados a las caracterısticas biológicas del sistema.

Profundizando el significado de los parametros relacionados a aspectos biologicos, Ibarz et al. (2011) senalan lo siguiente: el parámetro α cumple la funcion de identificar el voltaje de reinicialización relativo a las ramas estables e inestables de la nulclina rápida, σ desplaza la nulclina lenta de manera vertical en el plano de fases.

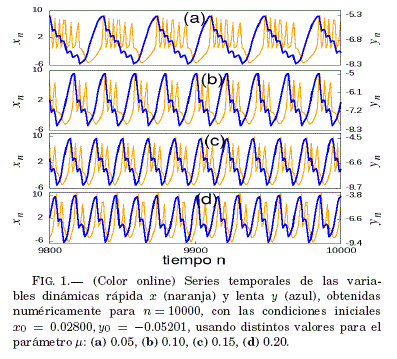
Ramírez-Ávila et al. (2015) realizaron un estudio detallado del modelo de Rulkov en relacion al parametro de actividad neuronal μ, en el cual se indica que dicho parametro debe tener valores positivos pequenos (μ < 1) para que se pueda reproducir el comportamiento neuronal regular. Por ejemplo, en la Fig. 1, se muestra la variacion en el comportamiento de las rafagas de picos en función del parametro μ.

En este trabajo, el parametro de actividad neuronal se mantuvo fijo μ = 0.1, debido a que Ramírez-Ávila et al. (2015) muestran que este valor esta asociado a valores de periodicidad pequenos de un comportamiento regular en la variable rápida x.

2.1. Caracterización del modelo de Rulkov

Para la caracterizacion del mapa de Rulkov, Ramírez-Ávila & Gallas (2011) proponen el cálculo de periodicidades como metodo alternativo al diagrama de bifurcacion y al cálculo de exponentes de Lyapunov.

La periodicidad se define como el numero de pasos (tiempo) n que transcurren hasta que la variable dinamica alcance exactamente el mismo valor, lo que permite visualizar en el espacio de parametros, estructuras regulares como por ejemplo regiones similares a patrones de troncos de palmera, llegando a tener una descripcion más detallada de los regímenes oscilatorios.

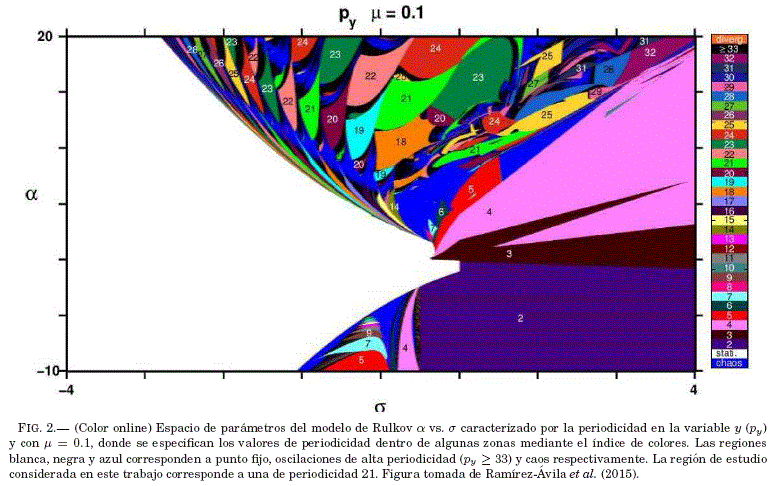
Cabe resaltar que en el modelo de Rulkov, Ramírez-Ávila et al. (2015) indican que los valores de la periodicidad en la varible rápida x y la variable lenta y son generalmente equivalentes; por lo tanto, en este trabajo se calcula la periodicidad de la variable lenta y por tener una forma similar a una oscilacion de relajación como lo muestra la Fig. 1. Ademas, se utilizó el plano de parámetros obtenido por Ramírez-Ávila et al. (2015), para un valor de μ = 0.1, como se muestra en la Fig. 2.

Pisarchik & Feudel (2014) senalan que el análisis de multiestabilidad de un sistema dinamico es muy importante debido a la coexistencia de varios estados estables iniciales posibles para un conjunto de parametros dados, donde el sistema depende crucialmente de las condiciones iniciales. Las condiciones iniciales que dan lugar a diferentes trayectorias que pueden converger a un atractor o no, se denomina cuenca de atracción.

El fenomeno de la multiestabilidad está presente casi en todas las areas de la ciencia; la primera vez que se utilizo el término multiestabilidad fue en el estudio de la percepcion visual de Atteneave (1971) donde se analiza un problema de perspectiva visual. En Biología, se tienen varios mecanismos y estructuras topologicas que conducen a la multiestabilidad; siendo la base para explicar fenomenos oscilatorios periodicos según lo señalan Ullner et al. (2007). En hidrodinamica, Ravelet et al. (2004) reportan la presencia de multiestabilidad asociada a la turbulencia de fluidos, a bajos y altos numeros de Reynolds. En optica, se tiene el fenómeno de la multiestabilidad espacial observado en un laser, donde se encuentran patrones espaciales debido a la interaccion de los modos de cavidad como lo muestran Brambilla et al. (1991). En reacciones químicas, Ganapathisu-bramanian & Showalter (1984) trabajaron con base en la biestabilidad de varias reacciones de oxidacion. En el analisis de ecosistemas, Huisman & Weissing (2001) dan un enfoque desde la dinamica no lineal mostrando que la coexistencia de diversas especies puede ser caracterizada por cuencas de atraccion de geometria fractal, donde una pequena perturbación produce un cambio en la biodiversidad del sistema; por lo tanto, una transicion a otro estado estable.

En dinámica neuronal, la multiestabilidad se presenta como mecanismo basico para explicar el contenido asociativo de almacenamiento direccionable y el reconocimiento de patrones, tanto en sistemas neuronales artificiales como los descritos por Hertz et al. (1991) y naturales estudiados por Canavier et al. (1993). A nivel de una sola neurona, la multiestabilidad indica la coexistencia de varios patrones de disparo de rafagas de picos (bursting), ya sean regulares o caoticos como lo reportan Braun & Mattia (2010), lo que constituye un aspecto interesante de este trabajo.

Para redes neuronales, Newman & Butera (2010) muestran que la multiestabilidad y particularmente la biestabilidad, juega un papel importante para explicar la senal celular y las interacciones neuronales, donde la llegada de un potencial de accion activa mecanismos excitatorios e inhibitorios a traves de neurotransmisores.

 

3. SINCRONIZACIÓN

La sincronizacion es un fenómeno emergente debido a la interaccion de osciladores que constituyen un sistema complejo. Puede surgir abruptamente en redes complejas biologicas según se muestra en Boc-caletti et al. (2016), donde los sistemas vivos tienden a ajustar sus ritmos en funcion a una interacción existente como lo senalan Manrubia et al. (2004). De acuerdo con Ramírez-Ávila (2007), se pueden distinguir diferentes tipos de sincronizacion, como por ejemplo: completa, generalizada, en fase, con retardo, con retardo intermitente y casi sincronizacion.

Para el estudio de la sincronizacion en neuronas modeladas por el mapa de Rulkov, Calderon de la Barca & Ramírez-Ávila (2017) usaron como indicadores de sincronizacion dos cantidades que involucran a la variable rápida x y a la variable lenta y. (i) El error medio de sincronización ⟨ε⟩ que se define como la distancia euclidiana promedio a la variedad de sincronizacion; por lo tanto, este valor debe tender a cero en las diferencias de las variables de cada oscilador para cada tiempo n en el caso de sincronizacion completa. Para dos neuronas de Rulkov acopladas se expresa mediante la siguiente ecuacion:

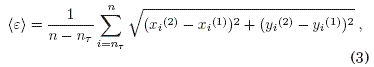
donde n_τ es un transitorio. (ii) El error máximo, que es el valor maximo de las distancias euclidianas para los n — n_τ valores, es decir:

con i = n_τ,...,n

3.1. Acoplamiento

Para modelar la interaccion sináptica entre dos neuronas i — j, Girardi-Schappo et al. (2018) utilizan un acoplamiento electrico de carácter bidireccional y simétrico, expresado por:

siendo n el tiempo, β^e una constante, g_ij los elementos de una matriz simetrica y de diagonal nula que define la conexion entre neuronas.

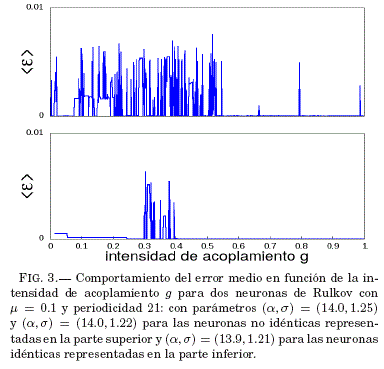
En la Fig. 3 se ve que tanto para neuronas identicas y no idénticas, las regiones de sincronizacion completa son bastante extendidas.

3.2. Heterogeneidad

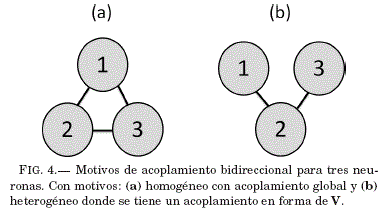
Estrada (2010) define la heterogeneidad de una red compleja en terminos de la topología de la misma; con base en las distintas distribuciones de conexiones que se puede tener entre los nodos de la red. Cuando el numero de nodos es pequeño cada estructura de red recibe el nombre de motivo. En nuestro caso, tenemos dos motivos (ver Fig. 4) para los cuales se estudiara la sincronización.

 

4. RESULTADOS

4.1. Multiestabilidad

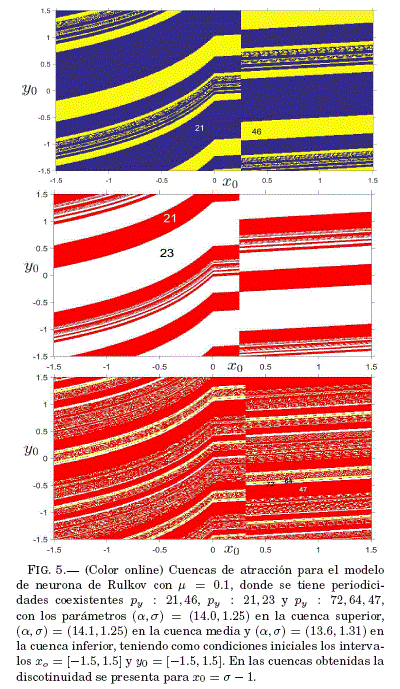
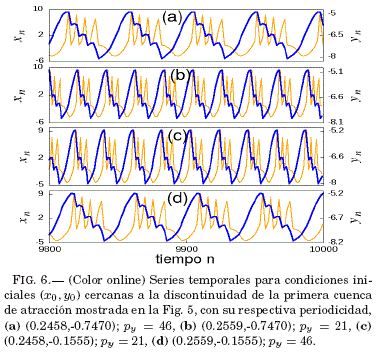
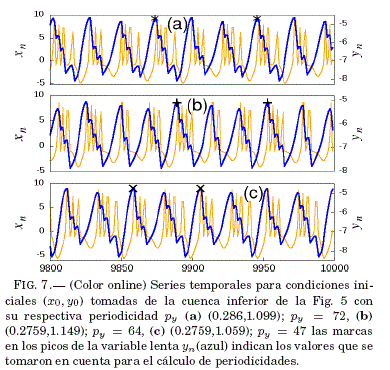
Las cuencas de atraccion de la Fig. 5 muestran la biestabilidad y la triestabilidad de la neurona de Rulkov, ademas de una discontinuidad para el valor x₀ = 0.25. Para analizar y confirmar la existencia de dicha discontinuidad se recurre a la obtencion de series temporales para condiciones iniciales en la vecindad de la misma, mostrandose en la Fig. 6 el caso de la cuenca superior de la Fig. 5. La triestabilidad observada en la cuenca inferior de la Fig. 5 se ilustra tambien mediante series temporales representadas en la Fig. 7.

La Tabla 1 muestra que para los experimentos numericos se tomó un conjunto de tres neuronas que comparten la misma periodicidad (p_y = 21); es decir, se encuentran en la misma region de periodicidad en la Fig. 2.

Para el estudio de sincronizacion de los motivos mostrados en la Fig. 4; primero se tomo en cuenta un trío de neuronas diferentes en los parametros según la Tabla 1; sin embargo, tenıan la misma periodicidad p_y = 21. Luego se considero un trío de neuronas identicas (caso 1) de la Tabla 1.

4.2. Trío de neuronas no idénticas

Motivo (a) de la Fig. 4.

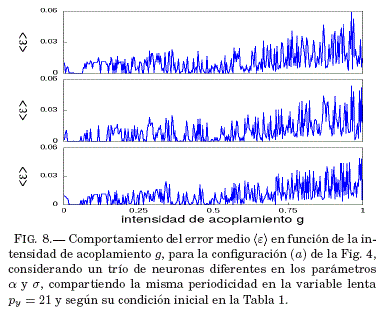
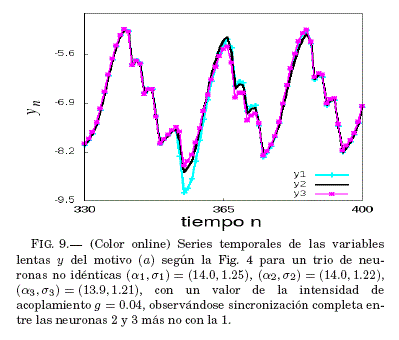
En la Fig. 8 se puede ver que para un valor de la intensidad de acoplamiento en la vecindad de g = 0.04, el error medio de sincronización ⟨ε⟩ tiende a ser nulo; por lo tanto, en la Fig. 9 se verifica si este valor de g lleva al sistema a la sincronizacion recurriendo a las series temporales de las variables lentas y de cada neurona.

Motivo (b) de la Fig. 4.

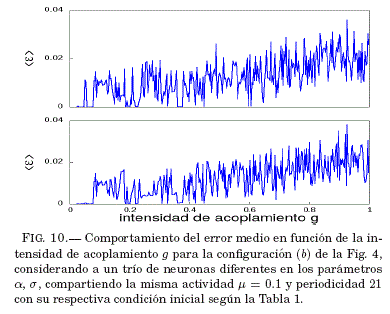
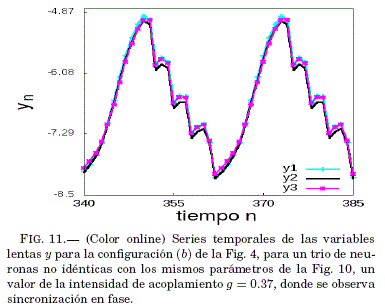
Como se puede ver en la Fig. 10, para valores pequenos de g y en la vecindad de g = 0.36 se tiene que el error medio de sincronizacion ⟨ε⟩ tiende a ser nulo. Así, en la Fig. 11 se verifica que para un valor g dentro de este intervalo el sistema sincroniza, lo que se muestra mediante las series temporales de las variables lentas y

4.3. Trío de neuronas idénticas

Motivo (a) de la Fig. 4.

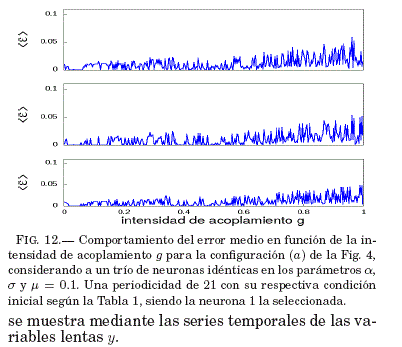
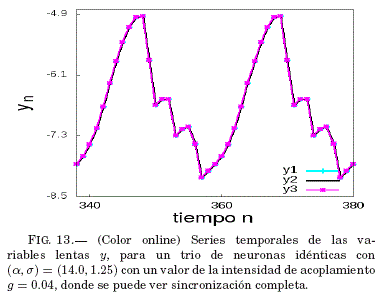
Como se puede ver en la Fig. 12, existe un intervalo para g donde el error medio de sincronizacion ⟨ε⟩ tiende a ser nulo; por lo tanto, en la Fig. 13 se verifica que este valor de g lleva al sistema a la sincronizacion como se ve en las series temporales de las variables lentas y con un valor de g específico.

Motivo (b) de la Fig. 4.

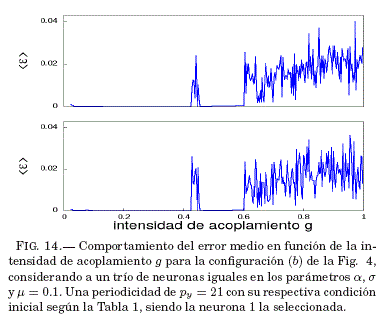
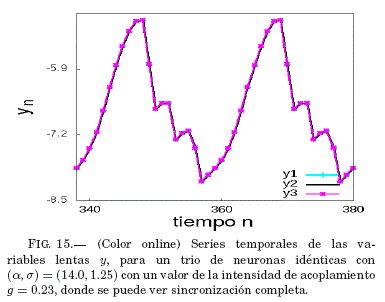
Como se puede ver en la Fig. 14 existe un intervalo grande para g = 0.36 donde se tiene que el error medio de sincronizacion ⟨ε⟩ tiende a ser nulo; por lo tanto, en la Fig. 15 se verifica que este valor de g lleva al sistema a la sincronizacion, lo que se muestra en las series temporales de las variables lentas y con un valor de g específico.

 

5. CONCLUSIONES Y PERSPECTIVAS

Se determino la sincronización en tríos de neuronas identicas y no idénticas caracterizadas por sus periodicidades que pueden ser las mismas o no. Se encontro el carácter multiestable de neuronas mediante la obtencion de las cuencas de atraccion, encontrando una discontinuidad en x₀ = σ - 1 verificandola mediante series temporales. Comparando los errores medios de sincronizacion de ambos motivos, se ve que la configuracion heterogenea facilita la sincronización.

Comparando el error medio de sincronizacion ⟨ε⟩ para motivos formados por 2 y 3 neuronas; se tiene como impacto principal la reduccion considerable del intervalo de valores de g que muestran sincronizacion (⟨ε⟩ → 0) incluso con neuronas no identicas.

Se tiene previsto trabajar con la determinacion de los tiempos de sincronizacion para poder responder de manera mas precisa a la cuestión anterior. Se tiene tambien como perspectiva trabajar con motivos de 4 y 5 neuronas para determinar si la heterogeneidad de las redes subyacentes a estos motivos juega o no un rol importante en lo que concierne a la sincronizacion. También, sería interesante abordar el problema de la multiestabilidad para diferentes regiones en el plano de parametros.

 

AGRADECIMIENTOS

Agradecemos a la Carrera de Física de la Universidad Mayor de San Andres y al I.I.F. por las facilidades que nos brindan para realizar investigacion en las mejores condiciones.

Conflicto de intereses

Los autores declaran que no hay conflicto de intereses con respecto a la publicacion de éste documento.

 

REFERENCIAS

Abarbanel, H.D., Szucs, A., Varona, P., Volkovskii, A., Rabinovich, M. & Selverston, A. (1999), Computacional Neuroscience 11, 563.         [ Links ]

Abarbanel, H. D. & Rabinovich, M. (2001), Current Opinion in Neurobiology, 11, 423.        [ Links ]

Atteneave, F. (1971), Scientific American 225, 63.         [ Links ]

Boccaletti,S.,Almendarl,J.A.,Guan,S.,Leyva,I.,Liu,Z.,Sendina-Nadal,I.,Wang,Z. & Zon,Y.(2016), Physics Reports 660,1         [ Links ]

Borisyuk, A., Friedman, A., Ermentrout, B. & Terman, D. (2005), Mathematical Neuroscience, (Berlín: Springer- Verlag).         [ Links ]

Brambilla, M., Lugiato, L., Penna, V., Prati, F., Tamm, C. & Weiss, C. (1991), Physical Reviews Letters 43,5114.         [ Links ]

Braun, J. & Mattia, M. (2010), NeuroImage 52, 740.         [ Links ]

Calderon de la Barca, I. & Ramírez-Ávila, G.M. (2017), Revista Boliviana de Física 30, 3.         [ Links ]

Canavier, C., Baxter, D., Clark, J. & Byrne, J.(1993), Journal of Neurophysiology 69, 2252.         [ Links ]

Estrada, E. (2010), Physical Review E 82, 066102        [ Links ]

Ganapathisubramanian, N. & Showalter, K. (1984), The Journal of Chemistry Physics 80, 4177.        [ Links ]

Girardi-Schappo, M., Tragtenberg, M. & Kinouchi, O. (2018), Journal of Neuroscience Methods 220, 116.         [ Links ]

Hertz, J., Krogh, A. & Palmer, R.(1991), Introduction to the Theory of Neural Computation, (New York, Addison-Wesley).         [ Links ]

Hodgkin, A.L. & Huxley, A.F. (1952), The Journal of Physiology 117,500.         [ Links ]

Huisman, J.& Weissing, F. (2001), The American Naturalist 157, 171.         [ Links ]

Ibarz, B., Casado, J. & , Sanjuan, M.A.F. (2011), Physics Reports 501, 1.         [ Links ]

Izhikevich, E. (2007), Dynamical Systems in Neuroscience: The Geometry of Excitability andBursting, (Cambridge: The MIT Press 505).        [ Links ]

Lamberti, W. & Rodríguez, V. (2007), Electroneurobiología 15, 31.         [ Links ]

Longstaff, A. (2011), Instant Notes in Neuroscience, (New York Springer-Verlag with BIOS Scientific Publishers).        [ Links ]

Manrubia, S., Mikhailov, A. & Zanette, D. (2004),Emergence of Dynamical Order: Synchronization Phenomena in Complex Systems, 2, (Singapur, World Scientific Printers).        [ Links ]

Newman, P. & Butera, R. (2010), Chaos 20, 023118.        [ Links ]

Nicolis, G. (1995), Introduction to nonlinear science, (Cambridge Great Britain, Ed. Cambridge).        [ Links ]

Pisarchik, A. & Feudel, U. (2014), Physics Reports 540, 167.        [ Links ]

Ramírez-Ávila, G.M. (2007), Revista Boliviana de Educación Superior 7, 25.        [ Links ]

Ramírez-Ávila, G.M. & Gallas, J. (2011), Revista Boliviana de Física 19, 1.        [ Links ]

Ramírez-Ávila, G.M., Gallas, M. & Gallas, J. A. (2015), Revista Boliviana de Física 27, 1.        [ Links ]

Ravelet, F., Marie, L., Chiffaudel, A. & Daviaud, F (2004), Physical Review Letters 93, 164.        [ Links ]

Rulkov, N. (2001), Physical Review Letters. 86, 183.        [ Links ]

Strogatz, S.H. (1994), Nonlinear Dynamics and Chaos. With Applications to Physics, Biology, Chemistry and Engineering, (New York, Perseus Books).        [ Links ]

Ullner, E., Zaikin, A., Volkov, E. & García-Ojalvo, J. (2007), Physical Review Letters 99, 148.        [ Links ]

Wickens, A. (1995), A History of THE BRAIN From Stone Age surgery to modern neuroscience, (London and New York, Psychology Press).        [ Links ]