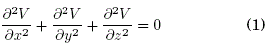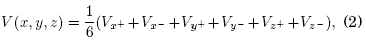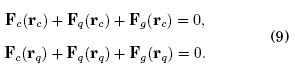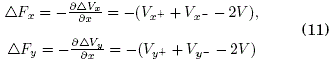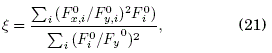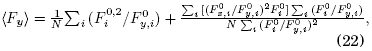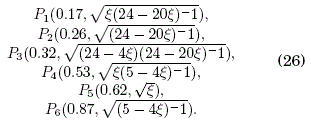Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
Compartir
Revista Boliviana de Física
versión On-line ISSN 1562-3823
Revista Boliviana de Física vol.33 no.33 La Paz dic. 2018
A. ARTÍCULOS
Modelo mínimo para la interacción eléctrica y gravitacional, en un sistema confinado de esferas cargadas
A minimal model for electrical and gravitational interactions in a confined system of charged spheres
D. Sanjines & F. Ghezzi
Instituto de Investigaciones Físicas Universidad Mayor de San Andrés
c. 27 Cota-Cota, Campus Universitario, Casilla de Correos 8635
La Paz - Bolivia
RESUMEN
Desarrollamos un arreglo experimental y una simulacion numérica para calcular la interaccion Coulombiana entre partículas cargadas confinadas. En este trabajo se ha elaborado un sistema de validacion, para establecer la interacción entre estas partículas y el contorno de confinamiento. Mediante la implementacion de un método de relajación para la ecuación de Laplace, usando una red 3D, podemos simular la configuracion de equilibrio para un sistema con pocas partículas. Ademas, se hace una comparación con el arreglo experimental con muchas partículas. Nuestra simulacion está, razonablemente de acuerdo, con la suposición de la interaccion Coulombiana.
Código(s) PACS: 41.20.Cv 02.60.Cb
Descriptores: Problemas con condiciones de contorno en electrostática, Ecuación de Laplace, Ley de Coulomb Modelos de simulación
ABSTRACT
We have developed an experimental set up and a numerical simulation to calculate the Coulomb interaction between confined charged particles. In this work we have elaborated a validation system to establish the interactions among these particles and the confining boundary. By implementing the relaxation method for the Laplace equation using a 3D grid, we can simulate the equilibrium configuration for a system with few particles. Also, a com-parison is made with an experimental set up with many particles. Our simulation yields a reasonable agreement with the assumption of a Coulombian interaction.
Subject headings: Boundary value problems in electrostatic, Laplace equation, Coulomb's law Model simulation
1. INTRODUCCTION
The physics of few-particle mesoscopic systems is an active and growing field of research. The scale of these systems is small enough for quantum effects to be considered, and yet of sufficient scale that classi-cal macroscopic laws still govern their behavior. Both experimental and theoretical approaches appear to support the assumption of an interparticle Coulomb interaction from which relatively simple macroscopic models emerge for several different systems, from nanotechnology to plasma research (Bonitz et al. 2008). However, crucial to research in this field is the determination and validation of the Coulomb interaction encouraging the development of new and in-teresting experiments at the macroscopic level and improving our understanding of phase transitions, packing of charged particles and other phenomena (Blonder 1985; Zheng & Grieve 2006). While at the mesoscopic level, light is being shed on the role of quantum effects in the critical behavior of the Coulomb system (Clark et al. 2009).
Over the years a number of theoretical models have been proposed with different repelling interac-tions, which include for example Coulomb, screened Coulomb, Lennard-Jones, dipole, logarithmic and hard sphere potentials (Jean et al. 2001; Schweigert et al. 1999). A recent experiment aimed at the determination and validation of the Coulomb interaction is that reported by (Zheng & Grieve (2006); Ghezzi et al. (2008)) (and references therein) consisting of several millimeter-sized metallic spheres lying on the lower plate of a parallel plate square capacitor. The spheres are laterally confined by a square metallic electrically charged boundary which prevents their dispersion in 2 D. One of the con-clusions reached is that no dipole interaction is ob-served and hence the remaining reasonable option is the Coulomb interaction. Furthermore the deformation of the ensemble of balls1 due to a gravitational gradient is measured inferring the nature of the re-pelling interaction aided by a computational method. This experiment belongs to a class of systems that are governed by the same physics, i.e., an interparticle interaction, a confining potential and an external potential (not to mention an eventual thermal activation). In the case that all of the above interactions have potentials that obey the Laplace equation with specific boundary conditions, we could then aim at numerically solving the equation of motion for the confined particles by means of the relaxation method where the physical interactions are incorporated via the corresponding boundary conditions in the confining border. In this work we take the experimental array referred to above (Zheng & Grieve 2006; Ghezzi et al. 2008) and apply the Laplace equation to construct a minimal model. We understand by a "minimal model" one which contains just the sufficient number of essential features that would characterize the relevant physical phenomena in the system. In our case these features are: the Coulombian repulsion field among the particles (millimeter-sized metallic spheres), the confining field between the square metallic border and the particles, and the gravitational field acting upon the system when this is tilted at a certain angle.
2. THE MODEL
The model which corresponds to the square parallel plate capacitor (figure 1) is a rectangular parallelepiped divided into 10 horizontal layers each containing 20 x 20 identical square boxes. When the tilting angle is zero the layers are perpendicular to the gravitational force, i.e., the system is level. The bottom and upper layers correspond to each of the parallel plates of the capacitor which have a definite electrical potential. The second layer from the bottom corresponds to the substrate in which the array of particles is located; only within this layer do the particles move according to the forces that yield the array to an equilibrium condition.
By assigning a definite electrical potential value to the box occupied by any particle at a certain instant, we can reproduce the physical condition that all particles are equally charged; since the particles move, the box with this definite potential will also move while its neighboring boxes have a potential that is to be determined numerically by solving the Laplace equation
in a 3D lattice. For our purposes, one of the most important properties of the solution of (1) is that the potential V(x, y, z) at some point (or box) is equal to the arithmetic mean of its six nearest neighbors in 3D,
where ![]() and similarly for y and z. The iterative numerical procedure by which (2) converges to a definite value of the potential at every point of the lattice is the well known relaxation method [17]. For simplicity we will take here-after adimensional units for the potential V(x, y, z) and for the coordinates x, y, z with unit increments Δx = Δy = Δz = 1 in a square lattice.
and similarly for y and z. The iterative numerical procedure by which (2) converges to a definite value of the potential at every point of the lattice is the well known relaxation method [17]. For simplicity we will take here-after adimensional units for the potential V(x, y, z) and for the coordinates x, y, z with unit increments Δx = Δy = Δz = 1 in a square lattice.
3. ELECTRICAL PLUS GRAVITATIONAL POTENTIAL LANDSCAPES
In order to avoid the dispersion of the particles due to the Coulombian repulsion, the square boundary has a definite potential which could be different from that of the particles but which we have considered as having the same potential in this work. This potential will be referred to as the "confining potential". Thus, we construct a model where each particle is found in a "potential landscape" created by the parallel plates and the square boundary. Such potential landscape is calculated by implementing recursively (2) through the whole parallelepiped divided in a grid of 10 x 20 x 20 boxes, although the relevant physics occurs in 2 D, that is, in the substrate where the particles would be allowed to move (figure 2). Therefore, the potential landscape results from evaluating V(x, y, z) vs. (x, y) keeping z = 2 constant (i.e., second layer from bottom to top). In figure 2 we have arbitrarily chosen the following boundary (non dimensional) values for the confining potential: V(x, y, 1) = 99 for the bottom layer, V(x, y, 10) = 0 for the top layer, V(±10, ±10, z) = 99 for the square boundary in each layer (2 < z < 9). The origin of the XY coordinate system of the layer where the particles are located is its geometrical center. In this landscape a single particle will move to the position with the minimum potential value, i.e., to the center of symmetry. When identical particles are included in the landscape, they will repel each other until all forces counterbalance and an equilibrium configuration is reached. Such a configuration is not so trivial to anticipate and a numerical evaluation of (2) through the relaxation method is necessary even for a system with few particles.
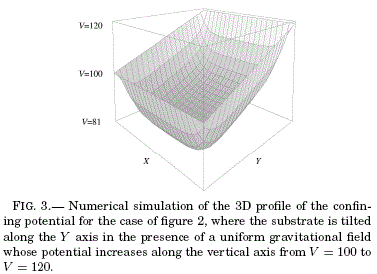
In figure 3 the potential landscape corresponds to a tilted substrate. In this case, the gravitational force manifests itself by means of a corresponding potential which increases uniformly in the positive Y direction, i.e., V(±10, y, 2) = y + 109 . Interestingly, this gravitational potential is considered only as an
additional boundary condition for the Laplace equation (1) which is added to the existing electrical potential due to both the confining boundary and to the charged particles. Furthermore, the particles will move in the resulting potential landscape calculated using (2) that contains simultaneously both the electric and gravitational interactions. As can be seen in figure 3, the particles will tend to move towards a different bottom position in this new potential landscape while repelling each other. This means that when compared to the level case, a different configuration of the particles will be reached.
4. DYNAMICS OF PARTICLES
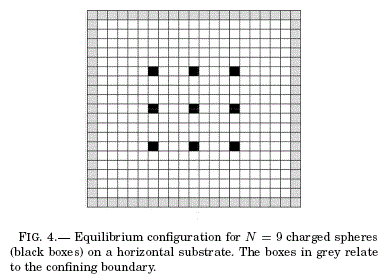
We chose the array of particles shown in figure 4 which is the equilibrium configuration when the substrate is level. In this symmetrical configuration of nine particles each particle produces a constant potential V0 = 99 in the box that it occupies. This potential V0 = 99 is also a boundary condition for the Laplace equation when solved numerically by (2). If this substrate is tilted the configuration in figure 4 is no longer in equilibrium and the particles will reach another final equilibrium configuration, i.e., each particle in figure 4 will start moving according to a dynamical rule that will be described below.
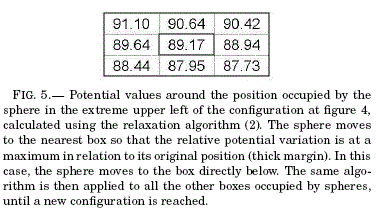
Take for example the particle located at the point (-4, 4), i.e., the particle at the upper left corner of the array in figure 4. Since this particle is considered as a "test charge", its dynamical state can not be affected by its own potential but rather by the rest of the charges in the space. We therefore substitute the value of V0 at (-4, 4) by the algorithm (2) and wait until the iterative routine stops. Then, we look at the potential values at (-4, 4) and its neighborhood. The result is shown in figure 5 where the heavy line border indicates the point (-4,4).
We notice by simple inspection that the potential at the point (-4, 3), just below the position of the particle, is the least of the potential values of its four nearest boxes. Consequently, the particle will move to this new position and its corresponding box will be assigned the potential value V0 because the new test charge will be in another position, say at (0,4). The process is repeated for the nine particles; the new resulting configuration will most probably be different from the original one.
How can we be sure that these dynamics make physical sense? The total energy of the new configuration has to be less than that of the preceding configuration. When the particles in a configuration have nowhere else to move (because they are localized in the bottom of a local potential valley found around each particle) and the energy of such a configuration is at a minimum, we can assume that we have reached the final equilibrium configuration. However, realizing that such an energy is actually the minimum might not be an easy task, since it may correspond to a metastable configuration which has less energy than its "neighbor" (or alike) configurations but has more energy than the real stable equilibrium configuration. We can test, with some degree of reliability, if a configuration is stable or metastable by "kicking" the configuration, i.e., moving the particles to a neighboring position, not necessarily the nearest, and comparing the energy changes. If the energy always grows after a few kicks, the configuration is most probably stable; if the energy diminishes after a few kicks, the configuration is metastable. Of course it is not guaranteed that the new configuration will be a stable one, because there could exist many metastable configurations, and the kicks may simply take the system from one configuration to another.
Another word of caution: the dynamical process leading to a final equilibrium configuration, although it might have physical sense, need not be the real dynamical process observed in an actual experiment. This is because in our model the allowed displacement of the particles is one box, either in the X or Y direction, per configuration. In a real experiment, each new configuration is defined by the instant positions of the particles, i.e., if T is the total time elapsed from the initial to the final configurations and we want to have N configurations, then one particular configuration corresponds to the positions of the particles at the time t = nT/N, with the integer n in the interval 0 < n < N. Therefore, in a real experiment, the particles' displacements could all be different, both in magnitude and direction. Nevertheless, and being conscious that the modeled dynamics can be different from the real one, we claim that the final equilibrium configuration characterized by a unique minimum of the total energy, isthesameinanycase. Differences will arise depending on how gross is the lattice's grid segmentation of the lattice's, i.e., the size of the box, which in turn will cause the equilibrium configuration to be reached in a longer time than the real one. Another possible difference is that in the model dynamics, a coarse grid segmentation will yield a final stationary oscillating state in which two different configurations (with a negligible energy difference) alternate, such that the real final configuration, having the minimum energy, can never be reached. The claim mentioned above is the matter of our current research and lies beyond the scope of this work.
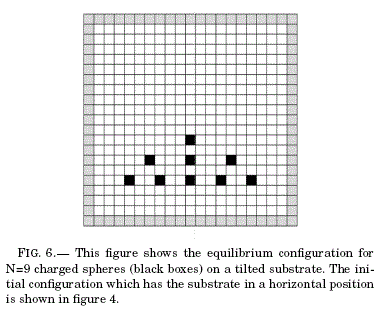
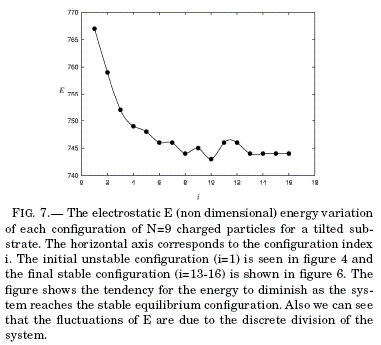
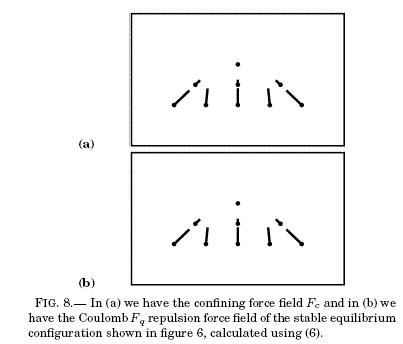
In figure 6 we have the final equilibrium configuration corresponding to the initial state depicted in figure 4 (in both cases we observe only the layer where the particles move). The black boxes represent the positions of the particles and the grey boxes determine the square confining boundary. The corresponding energy evolution is depicted in figure 7 (with energy values in the vertical axis and configuration index in the horizontal axis) where there are 13 different configurations including the initial and the final ones. The difference among configurations is not deduced from their energies; it was observed while the model dynamics were in course. Notice one interesting thing: the eighth and tenth configurations have less energy than the -supposedly- final configuration (the thirteenth) but in those configurations the particles had other allowed positions to move to, so we preferred to continue the model dynamics until it stopped or until it reached a stationary oscillating state. The former occurred first.
5. CONFINING AND REPULSIVE FORCE FIELDS
Next, once we achieve the potential energy field corresponding to figure 6, we can deduce its vector force field. This is done by implementing
for each particle in the 2D substrate lattice. We are purportedly ignoring the forces that are perpendicular to the substrate because they will cancel out with the corresponding normal forces. The derivative of V(x, y) with respect to x is (recall that we have set Δx = Δy = Δz= 1 in this work)
from which one can write
thus (3) results in
The confining force field in figure 8a was obtained by applying (6) to each of the equilibrium positions in figure 6 once the gravitational potential was set to zero (level substrate) and the V0 potential of each charge was substituted by the relaxation algorithm (2). Therefore, the resulting potential landscape Vc corresponds only to the confining interaction due to the charged boundary (lateral, top and bottom plates). In a similar way, we have obtained the repulsive force field among particles (figure 8b) by applying (6) to the potential field Vcq?Vc resulting in the subtraction of the confining potential field (Vc) from the potential field due to both the confining and Coulomb interactions among particles (Vcq).
We now recall that the equilibrium condition tak-ing into account all the interactions is
where Fc(ri) and Fq(ri) are the vector fields corresponding to the confining and repulsive forces respectively (figure 8) and ri is the respective position of the nine particle array; mgsenΘ is the field of "residua" forces corresponding to the gravitational interaction. Then, should the whole method applied in this work be consistent, it is expected that the gravitational force field can be obtained from the Fc and Fq fields according to (7).
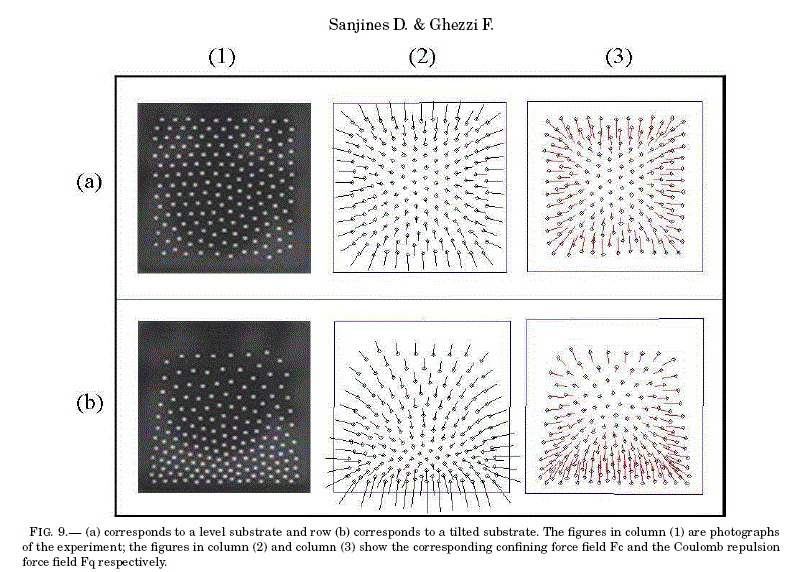
Figure 9 shows the corresponding confining (a) and repulsive (b) force fields for an actual experiment with a system of 169 particles (16). A distinctive feature that can be observed when one compares this latter figure with the simulated experiment in figure 8 is that in both cases there appears a kind of "equilibrium center" where the force is null, being the equilibrium center of the confining field in an upper position with respect to the center of the repulsive field. We can show that in the case of a level substrate these two equilibrium centers coincide; for a tilted substrate (as in figure 9) the distance between equilibrium centers will be proportional to some monotonous function of the angle of inclination. Knowing the particles configuration in equilibrium, it follows that we can obtain the residual gravitational force value Fg . To this end (7) is written as
and the expression is applied to the centres of equilibrium of charge rq and confinement rq that are assumed to be known through the configuration of the particles:
According to the hypothesis Fq(rq) = Fc(rc) = 0 and Fg(r) = Fg = const. (for any r), it follows Fg = -Fq(rc) = -Fc(rq). In view of the symmetry of the confinement field Fc as a consequence of the form (square) of the confinement border and the independent nature of the field in relation to the configuration of the particles in equilibrium, it is deemed better to evaluate the residual gravitational field in agreement with
Given that the confinement and gravitational fields are unique (for certain gradients of a tilted substrate) for the earlier expression (10) it is suggested that the centre of equilibrium of charge rq is the same irrespective of the number of particles. This speculation and also the efficient use of (10) to calculate the residual gravitational force field are interesting areas for further investigation.
6. ERROR ESTIMATION
A state of equilibrium (7) is equivalent to having a minimum energy in each site containing a particle. However, given that the error estimation in the 2D lattice is due to the finite size of a cell, then (4) shows a minimum energy potential error of ΔVx+ - V = V - Vx- along the X axis and an error of ΔVy = Vy+ - V = V - Vy- along the Y axis. The corresponding errors in the force components acting on each particle are
this would lead to the rewriting of (6) to include the follo wing error:
F is the net force on each particle, where F° is the computed force and its corresponding error ΔF is due to the cell dimensions. Now we demonstrate that |ΔFx| = |ΔFy| in (12). Taking into account that the particles only move within the XY plane of the substrate, there should not exist a net force along the Z axis perpendicular to the substrate. This translates into the condition Vz+ = Vz-=V in expression (2), where we obtain
Substituting this in (11) instead of V and readjusting terms we obtain the desired result
If we consider F° = F°f, defining α = |ΔFx| = |ΔFy| from (14), then the error of F° in (12) should be
where ƒ is unitary in the direction of F° . It can be seen in (15) that the error ΔF affects as much the magnitude as it does the direction of F° . We can reasonably assume that both magnitude and directional errors are of the order α and as such (12) is written as
where |ξ| < α and |η|<α (note that α,ξ and η have units of force). Developing (16) we arrive at the expression
where F is the magnitude of F° and Fx, Fy are its respective components. When necessary hereafter we will distinguish the magnitude and components of F from those of F° by adding the superscript for this last case.
When ξ y η are simultaneously zero in (17), then F = F°, as expected. However, we know that for physical reasons if F represents the residual force field corresponding to the gravity component along the inclined substrate in the direction of axis Y (figure 3), then from (7) we have that the sum of the confining force Fc and the Coulombian repulsion Fq should only contain components along the Y axis. As such, the F components along the X axis in (17) should be null for all particles. As we can see in graphs (a) and (b) of figure 8, Fc + Fq do not have null components along the X axis, we suppose that this is due to the errors discussed. Hence, equation (17) is subject to the following restriction
which results in F components only along the Y axis in (17). Substituting the value η of (18) in (17) we obtain
or equivalently
where the subscript i represents each one of the particles. So the F field in (19) is seen as a set of aligned vectors along the Y axis with different magnitudes. According to (7) these magnitudes should be equal. For this to happen we should apply the appropriate values of ξi for each particle. This is a time consuming and cumbersome process and we have therefore chosen the following criteria. We consider a unique value of ξ in (20) for all the particles and define the deviation as di = Fy,i - F°y,i so that S(ξ) = ∑i d2i has a minimum value, i.e., ðξ S = 0 and we obtain
where ξ only guarantees a minimum value of Fy,i in (20) with respect to an average value of Fy,iover all the particles N defined as
This expression provides a useful numerical estimation of the residual gravitational force that is obtained in the experimental set up when the plane is inclined. Thus, there must be a linear relationship between (Fy) the values and sine of the inclination angle.
Note that when a substrate is horizontal it is likely that some or all of the F°y,i values will be zero. In these cases (18) is used instead of (22) where ξ = -Fx = -F is obtained. In this case we need to define F = 0j to avoid an undetermined result in (19).
We apply (22) for a substrate at 4 different gradients such that θ1 > θ2 > θ3 > θ4 >. Since the gravitational field is homogeneous, the energy potential variation along the Z axis (figure 3) is ΔV = mgAz, where m is the mass of each particle. So, the substrate slope is Δz/Δx = tan = ΔV/(mgΔx). Since in this study the value of ΔV is not given in physical units but is non dimensional, and the mass of the spheres is an unknown parameter, we can only compare the different gradients among them and draw conclusions. The 9 angles are unknown but their ratios are known. The selected values are
where the configuration of figure 6 corresponds to θ3. For the configurations corresponding to the gradients given in (23), the non dimensional residual force values Fi (Fy =) shown in (22) are Fi = 1.360, F2 = 0.839, F3 = 0.725, F4 = 0.225, and from which the relevant quotients Fi,j = Fi/Fj are constructed:
Additionally, defining ξi,j = (senθi/senθj)2 , the relations in (23) are expressed as
and combine together with ξi,jξj,k = ξi,k and ξi,j = ξ-1j,i (according to the definition of ξi,j) to obtain all of the relevant combinations: ξ4,3, ξ4,2, ξ4,1 , ξ3,2 , ξ 3,1, ξ2,1. These values together with those of (24) serve to construct the points ![]() , These are used to verify if Fi α sen θi , where the gradient m of a linear adjustment of the points P should be close to 1. These points, ordered in ascending value of the abscissa, are
, These are used to verify if Fi α sen θi , where the gradient m of a linear adjustment of the points P should be close to 1. These points, ordered in ascending value of the abscissa, are
We define ξ = ξ2,1 as a variable parameter of which the gradient m(ξ) is dependent. The validity interval of ξ is calculated from the first relation in (23) obtaining:
Given that in (27) the minimum value of θ2 is θ° and the maximum value of θ2 is 90°, we obtain 0.25 < ξ < 1, then the slope m(ξ) for the 6 points in (26) is calculated using a linear fitting leading to an ascending monotonous function with extreme values m(0.25) ![]() 0.46, m(1)
0.46, m(1) ![]() 0.9 and mean values (m) = 0.67. Since we have
0.9 and mean values (m) = 0.67. Since we have
then the numerical results for m indicate that the relation Fi α sen θi is reasonably satisfactory (m ![]() 0.93) when the gradients are big (θ1
0.93) when the gradients are big (θ1 ![]() 90°). The discrepancies resulting from smaller gradients are at-tributed in this work to the coarse segmentation of the substrate (20 x 20 boxes) and the small number of particles (N = 9) involved which do no result in reliable residual force values in (22).
90°). The discrepancies resulting from smaller gradients are at-tributed in this work to the coarse segmentation of the substrate (20 x 20 boxes) and the small number of particles (N = 9) involved which do no result in reliable residual force values in (22).
7. CONCLUSIONS
We have constructed a "minimal" model to reproduce relevant features of a system of several electri-cally charged particles confined in a square parallel plate capacitor. Our approach embraces the theory of r-2 type interactions as well as data from actual experiments and numerical simulation.
The method employed for such a purpose is the solution of the Laplace equation in 3D by means of the relaxation method. The main results in this work are: (i) the final equilibrium configuration of a system of 9 particles, (ii) the corresponding energy evolution through the intermediate non-equilibrium configurations, and (iii) the vector force fields for the confining and repulsive interactions. These results are compared with those of the actual experimental set up with many particles (e.g., figure 9 with 169 particles) and a qualitative good agreement is found.
In this work, the solution of the Laplace equation is a scalar field of potential which can incorporate simultaneously all the different physical interactions (e.g., electrical and gravitational) as boundary conditions for the solution of the Laplace equation. The resulting vector force field deduced from the total potential field thus determines the dynamical behavior of the particles and the stable equilibrium configuration of the system.
Emerging from this work was the concept of an "equilibrium center" for the force fields (confining and repulsive) which may provide an alternative way for determining global characteristics of the particle system. Such an equilibrium center could move in an analogous way as does the center of mass of a particle system when acted upon by external forces.
Furthermore, we modeled the dynamics of the particles using a specific algorithm which results in a final equilibrium configuration exhibiting a minimum of the total energy. We suggest that although the actual dynamics of the particles may be different from the modeled dynamics, the final equilibrium configuration characterized by a unique minimum of the total energy is the same. The possible numerical differences arising between the model and the experiment is a consequence of the lattice's grid segmentation. We are pursuing further research so that our minimal model might eventually allow us to follow the true path of the particles towards their final equilibrium configuration. It is worth noting that within the goal of the model considered in this work, and in contrast with the experimental set up (Ghezzi et al. 2008), we use the minimum amount of relevant physical parameters to draw conclusions. Thus, we do not need to know explicitly the mass m of the particles, the gravity acceleration g nor the angle θ of inclination of the substrate. Instead, we use the ratios of the angles as in (23) and the ratios of the forces as in (24). We do not need either the physical values of the potential gradient ΔV and the dimensions of the substrate; it suffices to assign them non dimensional numerical values.
Finally, the implementation of our minimal model in this work suggests some interesting areas of research and as an educational aid for gaining insight and practice into these kinds of phenomena.
8. AKNOWLEDGEMENTS
The authors appreciate the help and collaboration of Grieve R and Zheng X, Queen's University Belfast and acknowledge support from Grant Project IDH, Universidad Mayor de San Andres (La Paz, Bolivia).
REFERENCIAS
Blonder, G. E. 1985, Phys. Soc., 30, 403 [ Links ]
Bonitz, M., Ludwig, P., Baumgartner, H., Henning, C., Filinov, A., Block, D., Arp, O., Piel, A., Kading, S., Ivanov, Y., Melzer, A., Fehske, H., & Filinov, V. 2008, Physics of Plasmas, 15, 55 [ Links ]
Clark, B. K., Casula, M., & Ceperley, D. M. 2009, Phys. Rev. Lett., 103,55701 [ Links ]
Frenkel, D. & McTague, J. P. 1979, Phys. Rev. Lett., 42, 1632 Ghezzi, F., Grieve, R., Sanjines, D., & Zheng, X. H. 2008, Revista Boliviana de Física, 14, 50 [ Links ] [ Links ]
Iwamatsu, M. 2003, Colloid Interf. Sci., 260, 305 [ Links ]
Jean, M., Even, C., & Guthmann, C. 2001, Europhys. Lett., 84, 3626 [ Links ]
Kong, M., Partoens, B., & Peeters, F M. 2003, New Journal of Physics, 5, 23 [ Links ]
Nurmela, K. J. 1998, Phys., 31, 1035 [ Links ]
Press, W. H., Flannery, B., Teukolsky, S. A., & Vetterling, W. T. 1992, Numerical recipes: The art of scientific computing . (Cambridge University Press) [ Links ]
Ryzhov, V. N & E.Tareyeva, E. 2002, Physica, 314, 396 [ Links ]
Schweigert, I. V., Schweigert, V. A., & Peeters, F M. 1999, Phys. Rev. Lett., 82, 5293 [ Links ]
S.Toxvaerd. 1980, Phys. Rev Lett., 44, 1001 [ Links ]
Tata, B. V. R., Rajamani, P. V., Chakrabarti, J., Nikolov, A., & Wasan, D. 2000, Phys. Rev. Lett, 84, 3626 [ Links ]
Zahn, K. & Maret, G. 2000, Phys. Rev. Lett., 85, 3654 [ Links ]
Zheng, X. & Earnshaw, J. C. 1998, Europhys. Lett., 41, 635 [ Links ]
Zheng, X. H. & Grieve, R. 2006, Phys. Rev., 73, 64205 [ Links ]