Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
Compartir
Revista Boliviana de Física
versión On-line ISSN 1562-3823
Revista Boliviana de Física vol.31 no.31 La Paz dic. 2017
HISTORIA
Teletransportación de fotones
Photon teleportation
Gabriel Alejandro Aguilar Michelle Balderrama
Instituto de Investigaciones Físicas, Carrera de Física
Universidad Mayor de San Andrés
c.27 Cota Cota, Campus Universitario, Casilla de Correos 8635
La Paz - Bolivia
*http://www.fiumsa.edu.bo/docentes/mramirez/
(Recibido 29 de noviembre de 2017; aceptado 20 de diciembre de 2017)
Resumen
El argumento Einstein-Podolsky-Rosen estableció las bases para discernir entre Teorías de Variables Ocultas y mecánica cuántica así como para desarrollar conceptos, tales como la teletransportación de partículas. El planteamiento de la paradoja ha evolucionado, simplificándose en algunos aspectos y llegando a ser formulado matemáticamente por John Bell; lo que permitió la realización de experimentos que determinen la validez de la mecánica cuántica e incursionar en la teletransportación de fotones. Los experimentos de Aspect mostraron que una de las desigualdades de Bell era quebrantada, con lo que las Teorías de Variables Ocultas no son correctas. Adicionalmente, la experiencia de Zeilinger tuvo éxito en la transportación de información mediante el uso de fotones anticorrelacionados.
Descriptores: Entrelazamiento cuántico - paradoja EPR - desigualdades de Bell - teletransportación - Mecánica cuántica - Formalismo mecánico cuántico - Información cuántica
Código(s) PACS: 03.65.-w - 03.65.Ca - 03.67.-a
Abstract
The Einstein-Podolsky-Rosen argument established the basis for distinguishing between Hidden Variable Theories and Quantum Mechanics, as well as, developing concepts such as particle teleportation. The approach of the paradox has evolved and has been simplified to the point that it was formulated mathematically by John Bell. This made possible experiments that determined the validity of quantum mechanics and made way for the exploration of photon teleportation. The experiments carried out by Aspect have shown that one of Bells inequalities was violated and, therefore, Hidden Variable Theories are incorrect. Moreover, the experience of Zeilinger has had success in teleporting information through the usage of anti-correlated photons.
Subject headings: Quantum mechanics - Quantum mechanics formalism - Quantum information
Conflicto de intereses Los autores declaran que no hay conflicto de intereses con respecto a la publicación de éste documento.
1 Introducción
Durante el establecimiento de la mecánica cuántica como teoría, se hicieron cuestionamientos a la validez de sus predicciones. Tal es el caso del plantemaniento de Einstein junto con sus entonces estudiantes Podolsky y Rosen, conocido como la paradoja Einstein- Podolsky- Rosen (EPR). Esta paradoja inicialmente pensada para refutar la teoría, sentó las bases para obtener la evidencia necesaria para sustentar la mecánica cuántica frente al punto de vista local y determinista. La premisa inicial de la paradoja EPR consistía en un gedankenexperiment 1 que mostraba que la mecánica cuántica era una teoría incompleta. Según la percepción de EPR, una teoría es completa si cada elemento de la realidad física tiene su contraparte en la teoría. Establecieron entonces un criterio para distinguir los elementos de la realidad: si se puede predecir con certeza el valor de una magnitud física sin pertubar al sistema, existe entonces algún elemento de la realidad física correspondiente a dicha magnitud.
El sistema del experimento planteado es un par de partículas entrelazadas alejadas entre sí a una distancia en la que no se puede comunicar información de una a la otra. Finalmente, se realiza una medición de un observable (que tenga su contraparte con la cual no conmuta, como son la posición y el momento) en una de las partículas; mientras que la otra adoptará un valor opuesto por el entrelazamiento. Según el criterio adoptado, al poder predecir el observable de la segunda partícula, entonces deben existir elementos de la realidad anteriores a la observación que determinen los valores asumidos por las variables; dichos elementos no son incluidos en la mecánica cuántica y, por lo tanto, es una teoría incompleta. Los defensores de la teoría cuestionada argumentaron que los observables no tienen realidad simultánea hasta que cada uno es medido independientemente; por lo tanto, no puede concluirse nada determinante a partir del anterior criterio. En cambio, el hecho de que al medir una variable de una de las partículas, la otra adoptase un valor de manera instantánea era una acción fantasmal a distancia según Einstein y solo podía ser explicada si se introducían variables desconocidas que preserven los criterios de localidad y causalidad. A estas teorías se las denominó genéricamente Teorías de Variables Ocultas (TVO).
Años más tarde se planteó una versión simplificada de la paradoja por Bohm & Aharonov , [1957]. Bajo el nuevo análisis se consideró el espín de dos partículas entrelazadas, de manera que no solo se redujo el problema a una sola variable, sino que cuantizó los posibles valores de las variables; puesto que, en cualquier experimento realizable, el espín de una partícula solo adopta uno de dos valores en una dirección en particular.
1.1 Teorema de Bell
En medio de este panorama, John Bell planteó la paradoja de manera formal, tomando en cuenta una teoría genérica de variables ocultas, basada en las ideas de localidad y determinismo para así obtener la correlación de los espines de partículas entrelazadas en un experimento de tipo Bohm. El resultado de su razonamiento concluyó con una serie de desigualdades que dicho sistema debía cumplir bajo la explicación de cualquier TVO; sin embargo, de violarse alguna desigualdad, ninguna TVO puede explicar el comportamiento de dicho sistema. El teorema de Bell se basa en dos hipótesis:
- Determinismo. Se refiere a la información suplementaria a la contenida en la función de estado para especificar completamente el valor de todos los observables de un sistema.
- Localidad. El producto de ambos observables dependerá, en general, del estado del par. A su vez toda información debe ser comunicada bajo los principios de la invarianza de la velocidad de la luz en el vacío.
Existen dos clases principales de TVO. Una recibe el nombre de no contextual, en la cual el estado completo del sistema determina el valor de una cantidad que se obtendrá mediante cualquier procedimiento de medición estándar de esa cantidad. La otra, que se suele llamar contextual, está definida como el valor obtenido que depende de qué cantidades se miden simultáneamente.
El teorema de Bell es el nombre colectivo de una familia de resultados, todos mostrando la imposibilidad de una interpretación local y determinista de la mecánica cuántica.
Estas desigualdades fueron reportadas y demostradas por Bell , [1964], una de ellas representaba el mayor conflicto entre la mecánica cuántica y las TVO's:
![]()
Sin embargo, por la dificultad de implementar las implicancias experimentales de la misma, se utiliza otra formulación de la desigualdad, reportada por Clauser, et. al. , [1969].
![]()
donde: ![]()
es la suma de las correlaciones de los 4 diferentes estados posibles de dos partículas A y B de un mismo par, denominados estados de Bell 2. Cada correlación se debe a las propiedades de ambas partículas de un mismo par. En tanto que la preservación de la igualdad requiere de la medición en 4 distintas orientaciones.
La importancia del resultado de Bell radica en colocar, por primera vez, la disyuntiva filosófica planteada por la paradoja EPR en términos cuantitativos susceptibles de verificación experimental. La conclusión inmediata fue que ninguna teoría realista y local puede estar de acuerdo con todas las implicaciones estadísticas de la mecánica cuántica.
Las cuestiones lógicas y metodológicas lidian con el problema de si se puede deducir legítimamente de estas investigaciones que la mecánica cuántica no es local, y si los datos experimentales prueban definitivamente que se han violado las desigualdades de Bell.
1.2 Teletransportación
El concepto de teletransportación subyace en la idea de que en experimentos como el planteado por Bohm-Aharonov, los espines de los electrones están anticorrelacionados, de manera que al medir uno de ellos el otro estará en dirección opuesta. Por lo tanto, si en el proceso de medición de la primera partícula se la entrelazara con otra cuyas propiedades quieren ser transportadas, entonces estas propiedades se transferirían a la segunda partícula debido al entrelazamiento inicial.
Estas ideas fueron fortalecidas con el desarrollo del formalismo cuántico 3 y experimentalmente demostradas con un análogo luminoso. Para tratar con este problema es necesario definir el estado de un sistema (denotado por ![]() , si este consiste de los espines de 2 partículas, que pueden ser arriba
, si este consiste de los espines de 2 partículas, que pueden ser arriba ![]() o abajo
o abajo ![]() , el estado genérico del sistema será:
, el estado genérico del sistema será:
![]()
donde los coeficientes zi elevados al cuadrado son las probabilidades de que el estado sea el término al cual modulan; por lo tanto, debe cumplirse que ![]() En el caso particular de un estado entrelazado de dos partículas A y B (denominado estado singulete) se tiene que el sistema está definido por:
En el caso particular de un estado entrelazado de dos partículas A y B (denominado estado singulete) se tiene que el sistema está definido por:
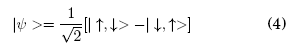
que indica que las orientaciones de los espines están anticorrelacionadas y que cada uno de los posibles estados tiene 50% de probabilidad de ser medido. La partícula A actúa como un intermediario para transportar la información; mientras que la partícula B es modificada según la información que recibe de A. Por otro lado, se cuenta con una partícula X, que es la que se quiere transportar y cuyo estado general es:
![]()
Entonces el estado inicial de los tres espines es 4:

donde cada subestado describe el espín de las partículas X, A y B en ese orden.
A partir de este estado, se deben realizar una serie de operaciones para alterarlo de tal manera que se transfieran las propiedades de X hacia B, es decir, atribuir los coeficientes del estado X a la partícula B. La serie de operaciones a realizar son:
-
Una operación C-X entre A y X, que es equivalente a cambiar la orientación del espín de A si y solo si el espín de X es abajo
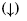
-
Medir el espín de A en una dirección (z).
-
Rotar el eje del espín 90°5 y medir el espín de X en esa dirección (x).
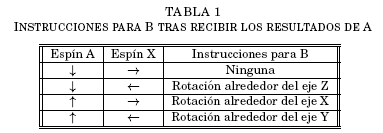
Una vez realizadas las mediciones, se deben enviar los resultados hechos por el manipulante de A y X al manipulante de B por cualquier otro medio, para que se realicen las operaciones finales descritas en la Tabla 1.
El resultado final es que, al haber medido el espín de las partículas A y X, ninguna conserva su estado inicial. Sin embargo, el estado final de la partícula B es una superposición de espín arriba (+) y abajo (-), con coeficientes a y b respectivamente, es decir, la información cuántica se ha transferido de la partícula X a la partícula B.
2 Metodología
2.1 Experimentos de Aspect
El científico suizo Alain Aspect verificó que la segunda desigualdad de Bell no se cumple luego de haber realizado tres experimentos entre 1981 y 1982, dos de ellos (el primero y el tercero) utilizaron medidas de un canal; mientras que el segundo utilizó medidas de dos canales y es el que proporcionó evidencias contundentes en contra de las TVO.
El primer experimento se detalla en Aspect, Dabilard & Roger , [1981] y consistió en la medición de la correlación de fotones polarizados en la región del visible. Los fotones de polarización correlacionada fueron obtenidos a través de decaimientos en cascada de átomos de calcio. El arreglo permitió obtener datos para diferentes distancias entre la fuente y los polarizadores, así como todo el rango de orientaciones relativas de los polarizadores (360°).
El segundo experimento fue, según Aspect, una transposición directa del esquema ideal de Einstein-Podolsky-Rosen-Bohm, así lo dio a conocer en Aspect, Grangier & Roger , [1982]. El arreglo se muestra esquemáticamente en la Fig. 1 y fue optimizado de tal manera que se midieron todas las orientaciones posibles de los fotones y no solo aquellas que coincidían con la orientación de los polarizadores. En este sentido, se reemplazaron los polarizadores lineales por otros de canales y seguidos de dos fotomultiplicadores; estas modificaciones asemejaron la medición de la polarización de los fotones a una medición de Stern-Gerlach de espines 1/2.
El tercer experimento hizo uso dos pares de polarizadores variables que poseían la propiedad de cambiar entre dos orientaciones en un tiempo corto (10 ns) comparado con el tránsito del fotón entre los polarizadores (40 ns). Las señales fueron captadas por un analizador de tiempo variable siguiendo el esquema de los anteriores experimentos. Este experimento se detalla en Aspect, Dalibard & Roger , [1982].
En su último experimento, Aspect utilizó polarizadores variables; sin embargo, la mayor dificultad, no resuelta en su experiencia, fue la aleatoriedad de la razón de cambio de orientación. Aspect trabajó con señales cuasiperiódicas que aún conservaban un carácter determinista. El problema surge a raíz de las condiciones de localidad al plantear el teorema de Bell, el cual impone que la elección de la dirección de medida debe ser aleatoria para asegurar que no haya comunicación física entre los polarizadores, a esta salvedad se la conoce como loophole de comunicación, que es un contrargumento de los defensores de las TVO.
2.2 Experimento de Zeilinger
En este contexto apareció Zeilinger , [2000] que explica el experimento de Innsbruck sobre la teletransportación de fotones. A diferencia del experimento de Aspect, la distancia de separación entre las estaciones de medición fue de 400 m, lo cual permitió que las orientaciones de los analizadores fueran aleatorias; dado que el tiempo de viaje de los fotones era mayor. En cuanto a los fotones, éstos fueron obtenidos por pulsos de luz ultravioleta (UV) que atravesaban un cristal. Los fotones se dirigían hacia sus respectivos destinos A y B mientras que un espejo reflejaba el pulso UV y atravesaba el cristal nuevamente para formar los fotones entrelazados C y D (ver Fig. 2). El fotón C ingresaba a un detector; por otro lado, D atravesaba un polarizador en cualquier orientación y se convertía en el fotón X. De esta manera, A y X incidían en un semireflector que ofrecía a los fotones la posibilidad de ingresar en 1 de 2 detectores. Sin embargo, si A y X se hacían indistinguibles, entonces existía interferencia cuántica y los fotones tenían una probabilidad de 25 % de ingresar en detectores separados. Esa probabilidad se correspondía con uno de los cuatro posibles estados de Bell.
Si se detectaban los fotones A y X simultáneamente en detectores distintos, entonces el fotón B era una réplica de X debido al entrelazamiento inicial de A y B.
3 Resultados
El primer experimento de Aspect fue importante para determinar que la correlación de la polarización de los fotones entrelazados se asemeja más a aquella predicha por la mecánica cuántica que por las TVO. Sin embargo, las técnicas utilizadas para realizar las mediciones perdían información; puesto que los detectores tenían baja eficiencia; por lo tanto, era imposible saber si los fotones no detectados eran bloqueados por el polarizador o solo no eran registrados por el detector.
El segundo experimento mostró resultados contundentes puesto que se trataba de una reproducción semejante a la del planteamiento inicial de la paradoja EPR. Con los polarizadores de canales acoplados fue posible determinar la orientación de los fotones; ya sea que tuvieran la orientación fijada por el detector o no. En consecuencia, se obtuvieron los coeficientes correspondientes a los 4 estados posibles del sistema.
El tercer experimento consideró la variación en el tiempo de la orientación de los polarizadores. Según Aspect y Bell, si existiera alguna interacción con una velocidad igual o cercana a la de la luz los resultados obtenidos podrían explicarse también a través de teorías de variables ocultas (o de parámetros suplementarios); por lo tanto, las desigualdades de Bell no se aplicarían en dicha situación y no habría disyunción entre la mecánica cuántica y las TVO's. Sin embargo, el arreglo experimental aseguró que dicha interacción no existe; puesto que la razón de cambio de los polarizadores es mayor a L/c.
En el experimento de Zeilinger se verificó que la polarización del fotón B coincidía con la del fotón X en un 80% de las veces y para diferentes orientaciones de polarización X. El factor más limitante para realizar el experimento fue la medición del estado de Bell entre los fotones A y X; puesto que para realizar el transporte de información es necesario que A y X sean indistinguibles. El equipo de Zeilinger siguió la propuesta de Zukowski según la cual los fotones debían incidir sobre filtros de banda espectral extremadamente corta, de ese modo, los fotones tenían una energía bien definida; y, por el principio de Heisenberg, con gran incertidumbre en el tiempo. Más allá de haber medido la polarización correcta la mayor parte de las veces, solo se logró el transporte para uno de los 4 estados de Bell posibles (estado en el cual los fotones A y X son detectados simultáneamente en detectores distintos). Por lo tanto, con este método es posible conseguir el transporte en un 25 % de las veces como máximo.
4 Conclusiones y discusión
A pesar de que la paradoja EPR fue planteada inicialmente con el propósito de cuestionar los resultados de la mecánica cuántica, estableció los fundamentos necesarios para determinar la validez de esta teoría frente a otras en las que subyace la idea de que se requieren de variables no definidas para completar la descripción de la misma.
La evidencia experimental basada en los fenómenos de fotones anticorrelacionados favorece a las predicciones de la mecánica cuántica, en este sentido, los experimentos del equipo de Aspect fueron determinantes para eliminar la incertidumbre acerca de la vigencia de alguna TVO. Y bajo los mismos principios se erigen las experiencias de teletransportación cuántica. Las experiencias de Zeilinger utilizando fotones, muestran un avance revolucionario en la concepción de la teletransportación.
La teletransportación de partículas es, en realidad, la réplica de información cuántica de una partícula utilizando el fenómeno de entrelazamiento. Sin embargo, no es posible utilizar aquel principio para la transportación a velocidades superlumínicas; puesto que, para reproducir la información cuántica de alguna partícula es necesaria la comunicación de mediciones y resultados intermedios por medios convencionales.
Agradecimientos
Los autores agradecen a Marcelo Ramírez por su apoyo y paciencia durante la etapa de investigación; de la misma manera, agradecen a Eduardo Palenque por la asistencia, sugerencias y correcciones brindadas a lo largo del desarrollo del trabajo.
Footnotes:
1El término alemán gedankenexperiment se refiere al planteamiento pensado de algún experimento sin recurrir a la experimentación propiamente
2Los estados de Bell son detallados en Bell , [1964]
3La formulación matemática del procedimiento ideal para la teletransportación de partículas entrelazadas se encuentra de forma detallada en Bouwmeester et. al. , [1997]
4La demostración rigurosa se muestra en Premelc , [2007]
5La medición del espín tras una rotación de 90° es equivalente a la medición en la dirección izquierda ![]()
References
Aczel, A. (2001), Entanglement The Greatest Mistery in Physics (New York: Four Walls Eight Windows) [ Links ]
Aspect, A., Grangier, P. & Roger, G. (1982), Phys. Rev. Lett., 49 (2), 91 [ Links ]
Aspect, A., Dalibard, J. & Roger, G. (1982), Phys. Rev. Lett. , 49 (25), 1804 [ Links ]
Aspect, A., Dabilard, J. & Roger, G. (1981), Phys. Rev. Lett., 47 (7), 460 [ Links ]
Bell, J. S. (1964), Physics Physique Fizika, 1 (3), 195 [ Links ]
Bohm, D. & Aharonov, Y. (1957), Phys. Rev., 108 (4), 1070 [ Links ]
Bouwmeester, D. and Pan, J. and Mattle, K. and Eibl, M. and Weinfurter, H. & Zeilinger, A. (1997), Nature, 390, 575 [ Links ]
Clauser, J. F., Horne, M.A., Shimony, A. & Holt, R. A. (1969), Phys. Rev. Lett., 23 (15), 880 [ Links ]
Einstein, A., Podolsky, B. & Rosen, N. (1935), Phys. Rev., 47 (10), 777 [ Links ]
Premelc, A. (2007), Quantum Teleportation (Ljubljana:University of Ljubljana) [ Links ]
Zeilinger, A. (2000), Scientific American 282 (4), 50-59 [ Links ]