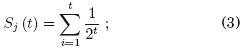ARTÍCULOS

 

Caracterización de un modelo social discreto de toma de decisión Basado en redes complejas

 

Characterization of a decision taking discret social model based on complex networks

 

 

Verónica Subieta-Frías* & Gonzalo Marcelo Ramírez-Ávila**
Instituto de Investigaciones Físicas, Universidad Mayor de San Andrés c. 27 Cota-Cota, Campus Universitario, Casilla de Correos 8635 La Paz - Bolivia
*veronica.subieta.f@gmail.com
**http://www.fiumsa.edu.bo/docentes/mramirez/
(Recibido 12 de julio de 2017; aceptado 21 de octubre de 2017)

 

---

Resumen

Se hace el análisis de la evolución de la opinión de un grupo de individuos bajo una situación de toma de decisión. Primero, se estudia el caso en el cual, los individuos del grupo no interactuan y solo están bajo la influencia de una fuente global externa constante, considerándose distintos tipos de conectividades entre la fuente y los individuos, pudiendo ser estas binarias o continuas, ya sean con intensidades constantes o variables en el tiempo. En segundo lugar, se analiza el caso en el que además de la fuente global externa, existe interacción entre los individuos, caracterizada por una red compleja. Posteriormente, se estudia el caso de la presencia de individuos denominados intransigentes en el grupo, los cuales tienen la característica de no modificar su opinión y por ende dificultar situaciones de consenso. Por último, se aborda el caso en el cual solo se tienen interacciones entre los individuos, sin considerar la fuente externa, encontrándose una sensibilidad a las condiciones iniciales en las opiniones individuales para la evolución del estado de opinión. En todos los casos, se analizan y comparan los efectos de las diferentes variantes del modelo en la opinión del grupo, siendo el alcance o no del consenso un aspecto esencial del estudio.

Código(s) PACS: 89.75.-k — 02.10.Ox — 05.50.+q — 89.65.-s

Descriptores: Sistemas complejos — Teoría de grafos — Modelo de Ising — Sistemas sociales

---

Abstract

We perform the opinión evolution analysis of a group of individuals under a decision-making situation. Firstly, we study the case of a constant global external source's action on the group whose individuals do not interact; considering different connectivity types be-tween the source and the group's members, namely, binary or continuous with constant or time-dependent intensities. Secondly, we analyze the case of a complex network featured interaction among individuals in addition to the action of the global source. After wards, we study the case in which there are the socalled inflexibles present in the group and whose main characteristic is that they are intransigent and opposed to changing their opinión thus, hindering consensus building. Finally, we address the situation in which there are only interactions between individuals, without considering the external source, this leads to a sensitivity towards the initial conditions of individual opinions for the evolution of the opinión state. In all cases, we analyze and compare the effects of the model variants on the group opinión, where the achievement or not of consensus is an essential aspect of the study.

Subject headings: Complex systems — Graph Theory — Ising model — Social systems

---

 

 

1. INTRODUCCION

El marco conceptual de la física estadística es muy general y esto llevo a la tendencia de aplicarla a nuevas áreas donde se tienen sistemas de muchas partículas interactuando entre sí. Este último hecho sumado al gran avance tecnológico que se dio en las últimas décadas, el cual permite el almacenamiento masivo de información y además la capacidad de realizar cómputos con gran rapidez, fue lo que motivo en los físicos el que traten de entender la conformación estructural y funcionamiento de las redes sociales con base en modelos de agentes en interacción.

El estudio de sistemas sociales a través de las redes complejas, como construcciones matemáticas susceptibles de análisis, tiene larga data. Así, se puede mencionar el experimento social llevado a cabo por Milgram (1967) y analizado en detalle por Travers & Milgram (1969), lo que sirvió como base para la formulación de las denominadas redes de mundo pequeño por Watts & Strogatz (1998). Por otra parte, Granovetter & Soong (1983) analizaron redes sociales con enlaces de diferente intensidad.

El concepto de centralidad en una red social, fue introducido por Bavelas (1948) y su interpretación conceptual completa fue dada por Freeman (1978), además con el respaldo experimental aportado por Freeman et al. (1979). También es importante resaltar el trabajo de Castellano et al. (2009) que explica la dinámica social desde una perspectiva de la física estadística. Por otra parte, Weidlich & Haah (1983) introducen conceptos y modelos con el fin de cuantificar aspectos sociales que van desde la economía hasta la interacción de poblaciones. Un análisis completo del desarrollo de redes sociales se encuentra en el trabajo de Freeman (2004), y un enfoque formal de modelos sociales es descrito por Helbing (2010). La detección de estructuras comunitarias en redes es planteada por Newman (2004), donde hace una revisión de métodos algorítmicos para encontrar comunidades densamente conectadas, siendo este un aspecto muy importante en redes sociales. Aunque hubieron muchos intentos de explicar sistemas sociales utilizando implícitamente el concepto de red compleja, solamente en los ultimos años se han desarrollado modelos que trascienden las analogías para convertirse, como lo señalan Newman et al. (2006), en modelos de simulación de la realidad. En años recientes, el estudio de redes complejas ha adquirido gran importancia en diferentes contextos y ha sido desarrollado formalmente con contribuciones tales como la de Barabasi & Albert (1999) que estudia el surgimiento de leyes de escala en redes aleatorias con aplicaciones en diferentes tipos de sistemas que se aproximan al mundo real. El boom que ha alcanzado el estudio de redes complejas ha dado lugar a que se tengan excelentes trabajos de revisión tales como el de Strogatz (2001), donde sistematiza el estudio de redes complejas de acuerdo a su naturaleza: mundo pequeño y libre de escala, prestando particular atención a aspectos relacionados con la sincronización; en la misma línea se puede mencionar a Arenas et al. (2008) quienes consideran procesos de sincronización en diferentes tipos de sistema yendo desde físicos a sociales, todos ellos caracterizados por redes complejas y finalmente a Wu (2007) y Lu & Qin (2011) quienes hacen un estudio exhaustivo de la sincronización en redes complejas. La estructura de redes complejas ha sido también ampliamente analizada por Boccaletti et al. (2006) y por Estrada (2011). Los procesos dinámicos en redes complejas han merecido la atención de Barrat et al. (2008) quienes estudian, entre otras cosas, conceptos tales como la transición de fases, la resiliencia y la robustez en redes. La omnipresencia e importancia de las redes complejas ha producido que se trate de popularizar este tema de estudio; así, se tienen excelentes libros de divulgación como el de Barabási (2002) y el de Caldarelli & Catanzaro (2012).

Los individuos que conforman los sistemas sociales son entes con muchas características distintas entre sí, tales como género, religión, edad, etc. que pueden ser utilizadas para la construcción de una red social compleja. La complejidad manifiesta en las interacciones sociales es muy grande que a veces sería imposible de describir las mismas con relaciones simples y pocos parámetros. Es así que para modelar redes sociales se deben hacer grandes simplificaciones del problema real. Las propiedades cualitativas e incluso algunas cuantitativas de los fenómenos a gran escala no dependen de los detalles microscópicos de los sistemas. Solo las características de mayor nivel tales como simetrías, dimensionalidad o leyes de conservación son relevantes para el comportamiento global, tal como lo señalan Castellano et al. (2009).

En las sociedades humanas al igual que en los sistemas físicos, se dan transiciones de fase o cambios del desorden al orden como el adquirir un consenso de la población respecto a un tema dado. Este tipo de comportamiento social llamado, desde el enfoque de la física estadística, como fenómeno macroscópico, es la inspiración para intentar comprender las regularidades alcanzadas globalmente, es decir, son efectos a gran escala o efectos colectivos que surgen de la interacción entre individuos independientes considerados como entidades relativamente simples. El objetivo es ver como las interacciones entre los individuos o agentes sociales permiten alcanzar consensos de opinión; es decir, es posible generar una situación de orden a partir de un estado inicial de desorden (opiniones diversas). Si no hubiesen interacciones, la heterogeneidad o desorden predominaría y cada individuo escogería una opinión personal a situaciones y problemáticas comunes al grupo. El factor clave es la interacción de los individuos entre sí y/o con una fuente global; siendo está interacción la que produce una tendencia en los individuos a tener opiniones cada vez más similares. Entonces, teniendo en mente el concepto de universalidad, se puede modelar los sistemas sociales tomando solo las propiedades más simples e importantes de un solo individuo buscando las características cualitativas generales que caractericen su comportamiento en los modelos.

El presente trabajo está estructurado del siguiente modo: en la Sec. 2 se describe el modelo de toma de decisión utilizado bajo ciertas circunstancias que exige la coyuntura. Posteriormente, se presentan los resultados de cada una de las situaciones estudiadas. Así, en la Sec. 3 se considera la situación en la cual solo existe la acción de una fuente global sobre los individuos. El caso en el cual además de la fuente global, existe también interacción entre individuos es descrito en la Sec. 4. La introducción de individuos intransigentes quienes no cambian de opinión en el modelo se expone en la Sec. 5. La situación en la que solo existe interacción entre individuos y no actúa una fuente global externa es desarrollada en la Sec. 6. Finalmente, se exponen las conclusiones y perspectivas de está investigación.

 

2. MODELO

Como punto de partida, consideramos un modelo de red social similar al planteado por Bassett et al. (2012), el cual está basado en una evolución discreta. La red consiste de N individuos (agentes) y cada uno de ellos tiene una variable de estado

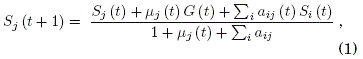
con j = 1, 2,..., N; donde S_j(t) es el estado de opinión al tiempo t y S_j(t) . El estado de opinión de un agente S_j(t) cambia con el tiempo como resultado de la información recibida de:

1.  Una fuente vía una emision global; por ejemplo a través de la radio o televisión.

2.  El estado de opinión de todos los agentes que conforman la muestra, transmitido mediante la red de contactos entre agentes.

Para especificar los dos aspectos citados anteriormente, aclaremos el concepto de fuente global y red social:

Fuente global. Es un agente especial externo de información que influye sobre todos los individuos pero no recibe la acción de estos. El valor que es emitido por la fuente global, al tiempo t se representa por G(t) En este trabajo, se toma el valor de G(t) = 1. Se asume que la recepción de está opinión por el agente j está dada por (t); si está variable es nula, el individuo no recibe la información de la fuente; por ejemplo será el caso en que se agotó la batería de su smarthphone, o se encuentra fuera del radio urbano, donde no llega señal de ningún tipo, etc. Esta fuente es el primer conductor externo de la dinámica del grupo.

Red social. La acción de compartir opiniones entre contactos es binaria, y está representada por los elementos de la matriz de adyacencia a_ij. Estos elementos toman el valor de 1 si el individuo i comparte su opinión con el individuo j. Según el caso real con el que se este tratando, se la puede considerar simétrica, si cuando interactúan los individuos intercambian opiniones, lo que ocurre por ejemplo al comunicarse mediantes celulares. La situación no simétrica se da por ejemplo en el caso de intercambio de opinión en una red social (facebook, twitter, etc), en el que uno de los individuos publica su opinión, pero no necesariamente sus amigos responderán a esa publicación. En este trabajo, la matriz es considerada simétrica. La diagonal de la matriz es nula pues la opinión de un individuo no influye sobre la suya propia. La naturaleza discreta de está regla de actualización es consistente con el hecho de que la información es a menudo obtenida en unidades discretas de tiempo de diferentes tipos de fuentes: sociales, tecnológicas o gubernamentales.

 

3.   DINAMICA DE OPINIÓN BAJO LA INFLUENCIA DE SOLO UNA FUENTE DE EMISION GLOBAL

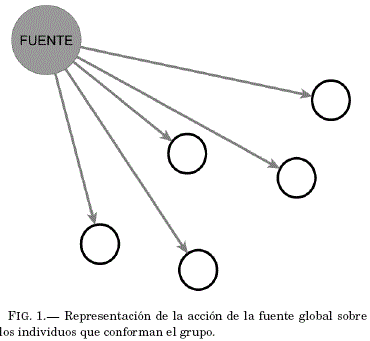
Se estudia el caso cuando no existe interacción entre los individuos, solamente actúa una fuente de emision global de opinión que influye sobre los mismos. Por otro lado, la opinión de los individuos no influye en la fuente global; es decir, los vínculos de influencia existentes entre la fuente y los individuos son unidireccionales, van de la fuente hacia los individuos, como se muestra en la Fig. 1.

En este caso, la Ec. (1) queda:

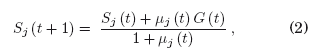
donde S_j(t) representa el estado de opinión del individuo j-ésimo a un tiempo t, _j(t) representa la conectividad del individuo j-ésimo con la fuente de emision global y G(t) representa la intensidad de emision de la fuente. En la Ec. (2) consideramos que la opinión inicial de todos los individuos es cero.

Se trabaja con una intensidad de la fuente global constante e igual a 1, es decir

Se analizan cuatro casos distintos de conectividad j; primero, la denominada conectividad binaria que se da cuando la conexión de los individuos con la fuente global ocurre o no; es decir toma los valores discretos 0 o 1:

la cual puede ser constante o variable en el tiempo. Luego, se consideran otras dos posibilidades cuando la conectividad con la fuente es de diferente intensidad o continua (vínculos pesados), es decir que toma valores entre 0 y 1.

que igualmente puede ser constante o variable en el tiempo.

Se realizaron experimentos para estos cuatro casos y se obtuvo:

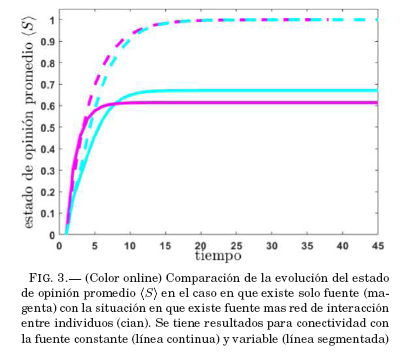
: Conectividad fuente-individuo discreta y constante en el tiempo. La evolución del estado de opinión de cada individuo no conectado ( = 0) permanece nulo; en tanto que el correspondiente a los siempre conectados ( = 1) evoluciona. Mediante un desarrollo analítico se obtiene:

es decir, la evolución del estado de opinión es una función creciente y tiende asintóticamente a su máximo valor posible que es la unidad, como lo indica la Ec. (3). además, se tiene consenso, de los individuos conectados durante toda la evolución del estado de opinión. Debido a que los individuos desconectados permanecen siempre en está situación no se tendra evolución de su estado de opinón que se mantiene nulo; por tanto, al promediar el estado de opinión de la muestra, este no podrá alcanzar el máximo valor.

: Conectividad fuente-individuo discreta y variable en el tiempo. En está situación, los experimentos deben realizarse sobre intervalos de tiempo lo suficientemente largos, de manera que se garanticen cambios en la conectividad fuente-individuo. Para ejemplificar lo anterior, se puede pensar en un escenario donde los individuos pueden conectarse o desconectarse de la fuente de acuerdo a la disponibilidad y al uso de un determinado dispositivo: teléfono inteligente, tableta, etc. Se tiene en este caso, a diferencia del de conectividad constante, que el estado de opinión de los individuos no es el mismo en cada paso de tiempo pero sí se alcanza consenso con el valor máximo posible del estado de opinión después de tiempos largos. El tiempo o número de pasos necesarios para alcanzar el estado de equilibrio, igual a la unidad, depende de la probabilidad de conectividad que hayan tenido los individuos en cada paso de tiempo, siendo el mínimo igual a 17 pasos, correspondiente a un 100% de conectividad, resultado que coincide con el hallado en el caso de conectividad constante.

: Conectividad fuente-individuo continua y constante en el tiempo. Cuando se considera el caso en que la conectividad fuente-individuo toma valores continuos entre 0 y 1 siguiendo ya sea una distribución uniforme o una gaussiana, (se hizo el análisis para ambas distribuciones), todos los individuos que tienen una conectividad distinta de cero alcanzan el máximo valor posible del estado de opinión; lo que se logra después de cientos de pasos.

: Conectividad fuente-individuo continua y variable en el tiempo. La conectividad promedio determina el tiempo de alcance del máximo valor posible del estado de opinión, el mismo que decae potencialmente a medida que aumenta el valor de la conectividad promedio. Así, para conectividades promedio de 8%, 20% y 50% se tienen respectivamente 255, 90 y 28 pasos de tiempo.

 

4. DINÁMICA DE OPINIÓN BAJO LA INFLUENCIA DE FUENTE DE EMISION GLOBAL E INTERACCIÓN ENTRE INDIVIDUOS.

Se estudia ahora la evolución del estado de opinión de un grupo de N individuos, pero a diferencia de la Sec. 3 que marco los primeros líneamientos, se considera además de la fuente global, la interacción entre individuos; es decir, ahora existe una red compleja. En la Fig. 2 se muestra la red resultante y las interacciones entre sus elementos. Nótese que las interacciones entre individuos (flechas de color negro) pueden ser bidireccionales a diferencia de las acciones que ejerce la fuente (flechas de color gris), esto significa que los individuos pueden intercambiar opiniones e influirse mutuamente. La interacción entre los individuos se caracteriza mediante los elementos de la denominada matriz de adyacencia a_ij que dan cuenta de los vínculos entre los mismos. Los elementos de está matriz toman los valores de 0 en la posición (i, j), si el individuo i no está vinculado al j y 1 en caso contrario. La matriz de adyacencia en este trabajo es simétrica porque se consideran vínculos bidireccionales. Se aplica entonces el modelo presentado en la Ec. (1), para ver como evoluciona para establecer la evolución del estado de opinión promedio del conjunto de individuos. Con base en el modelo propuesto por Erdos & Rényi (1960), se construyen grafos (redes) aleatorios que caracterizan los valores de ,j(t) y a_ij(t) lo que permite establecer el grado de conexiones promedio de los individuos, fa, aspecto que se explica con mayor detalle en la Sec. 4.2. Estos datos iniciales permitirán realizar las simulaciones numéricas.

4.1. Resultados y comparación con el caso de interacción solo con la fuente

Se quiere contrastar los resultados del modelo cuando se consideran conjuntamente la red y la fuente de emision global, comparados con los casos en que solo se tiene está última.

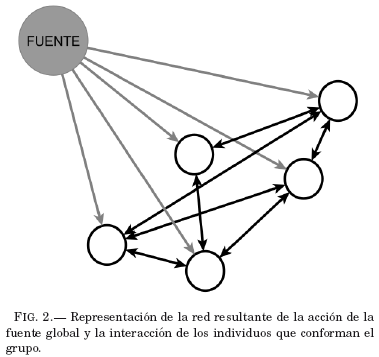
En la Fig. 3 se muestran los resultados obtenidos, cuando la probabilidad de conectividad permanece constante (línea continua) y cuando la probabilidad de conectividad es variable (línea segmentada). Las gráficas que se presentan en color cian corresponden a experimentos en los que se tiene fuente global y red de individuos interactuantes, caracterizada por la matriz de adyacencia. Las gráficas en color magenta corresponden al caso en que solo hay fuente de emision global.

Se observa en la Fig. 3 que las líneas representando , constante, (línea continua) se estabilizan para valores de, donde (S) se torna constante. El valor de estabilización de (S) corresponde a un valor máximo para está situación y al que denotaremos por (S)_MAX. La estabilización de (S) significa que la opinión de cada individuo, puede diferir de las opiniones de los demás individuos, pero después de un transitorio, el promedio se mantiene constante en el tiempo; es decir, las opiniones individuales pueden estar variando en el tiempo pero el promedio del grupo no se modifica. Como ya se vio en la Sec. 3, el estado de opinión promedio máximo (S)_MAX (en el caso de conectividad \i a la fuente constante), no es igual a la unidad y como se ve en la Fig. 3 tampoco cuando se añade la red (curvas cian y magenta de línea continua respectivamente). La gran contribución de la red es que cuando está introducción se alcanza un (S)_MAX que es mayor, al caso en el que no se la considera. Nótese que (S)_MAX con red compleja (cian) es mayor que (S)_MAX sin está característica (magenta). Si definimos el tiempo de estabilización como el tiempo en el cual (S) se torna constante; es decir, cuando el estado de opinión alcanza un valor máximo (S)_MAX, podemos ver que la estabilización ocurre para tiempos mayores que en el caso en el que solo actúa la fuente. Cuando se considera a la red, se alcanza (S)_MAX en tiempos mayores pero en compensación, el valor de este es mayor a (S) cuando no existe red.

Nótese que en los primeros pasos de tiempo, cuando no se considera a la red, la pendiente de la curva magenta es mayor a la pendiente de la cian; esto quiere decir que la evolución al principio es más rápida cuando no hay red; la presencia de la red ralentiza el ritmo de cambio, pero luego las curvas se intersectan y el comportamiento de las pendientes de las mismas bascula, ocasionando que en el caso donde solo actúa la fuente global, la estabilización ocurra antes que en el caso donde exista una estructura de red compleja.

De las curvas en línea segmentada, que corresponden al caso en el que la conectividad de los individuos con la fuente cambia a cada paso de tiempo, se tiene que, como se vio en la Sec. 3, siempre se alcanza la situación (S) = 1; es decir, que se llegue al estado de opinión máxima.

Para que el estado de opinión promedio máxima sea (S)_MAX = 1, cada uno de los individuos debe tener un estado de opinión individual igual a la unidad; es decir, se tiene consenso. Lo anterior es lo que diferencia del caso en el que la conectividad es constante. Por otra parte, se tiene también que la rapidez de evolución antes de la intersección es mayor y el tiempo de estabilización es menor cuando no hay red.

4.2. Caracterización de la evolución del estado de opinión promedio (S)

Se quiere caracterizar la evolución del estado de opinión promedio y para ello se analiza cómo influyen las distintas variables involucradas en este modelo. Para esto, se llevan a cabo experimentos en cada uno de los cuales se varían dos magnitudes, primero el tamaño de la muestra o número de individuos N y segundo, el grado de conexiones promedio de los individuos entre sí, fa que es un indicador del promedio del número de vínculos que tiene cada individuo. La determinación de fa se la hace mediante la construcción de grafos aleatorios siguiendo el modelo de Erdós-Rényi. Por ejemplo, si fa = 1, significa que todos los individuos se hallan vinculados con todos los demás, por lo que la matriz de adyacencia será una matriz de tamaño N x N cuyos elementos serán todos iguales a 1, excepto los de la diagonal que tomaran el valor 0. Los valores de la diagonal son 0 porque un individuo no puede interactuar o influir sobre sí mismo. Si el valor de fa es por ejemplo 0.2, significa que cada individuo estará conectado solo con el 20% de los individuos que conforman la red, o en otras palabras, si se cuenta el número de unos en una fila o columna de la matriz de adyacencia (da lo mismo porque se trata de una matriz simétrica), este será tan solo el 20% del número total de individuos N.

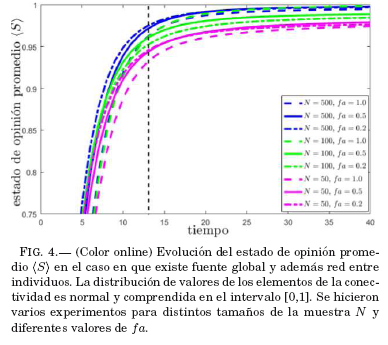
Se realizaron nueve experimentos cuyos resultados se presentan en la Fig. 4, notándose que en todos los casos se tienen comportamientos similares. El cambio drástico de pendiente se da aproximadamente después de 13 pasos de tiempo, en todos los casos, lo que se indica con una línea segmentada, vertical y negra. Antes del cambio de pendiente, la evolución de (S) es muy rápida lo que denominamos la primera etapa; en tanto que la segunda etapa ocurre después de este cambio.

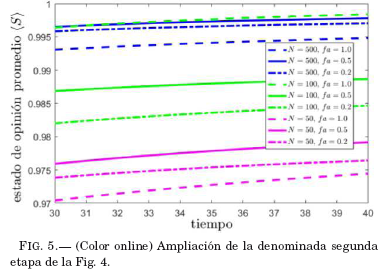
Durante la segunda etapa, se observa que la evolución de (S) se ralentiza y que la pendiente de la curva tiende a cero; es decir,(S) se aproxima asintóticamente a un valor máximo (S)_MAX Este estado de opinión máximo es estacionario. También, se puede ver que el valor de (S)_MAX depende proporcionalmente del tamaño de la muestra N. Para ver como afecta el grado de conexión entre individuos fa, en la Fig. 4 se amplifica la región de estabilización correspondiente a la segunda etapa de la (Fig. 5). Es importante resaltar que las diferencias entre (S)_MAX alcanzados para distintos fa son menores al 0.5% por lo que se puede obviar este análisis.

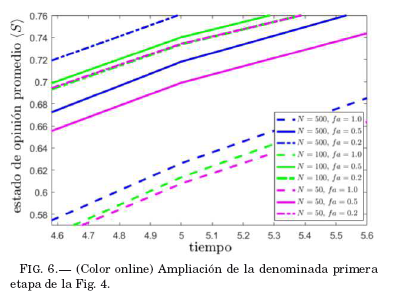
En la magnificación de la primera etapa de la Fig. 4 que se muestra en la Fig. 6, se observa que las curvas estan dispuestas según el valor de fa. Nótese por ejemplo que las curvas que corresponden a fa = 1 (línea segmentada), estan próximas; a continuación, siguen las curvas que corresponden a fa = 0.5 (línea continua) y por último, las curvas que corresponden a fa = 0.2 (línea punto segmento). Las curvas que representan a la red más homogénea en la primera etapa dan como resultado (S) con menor valor de lo que se obtiene con redes menos homogéneas.

En resumen, en la primera etapa, la homogeneidad de la red es más importante que el tamaño de la misma. Lo contrario a esto es lo que sucede en la segunda etapa, donde lo preponderante es el tamaño de red y no cuan homogénea es la misma.

Se define como consenso al estado en el cual todos los individuos adquieren una misma opinión debido a la interacción entre ellos. Muchas veces el consenso es un factor determinante en las sociedades, pues en situaciones reales, se presentan casos en los cuales es necesario para un grupo alcanzar decisiones compartidas. Los acuerdos o consensos logran una posición más fuerte y amplifican su impacto.

Un indicador estadístico que estaría directamente relacionado con este concepto y que puede ser usado para definir el grado de consenso alcanzado, es la desviación estándar. Cuando se tiene un grupo de individuos, se puede calcular en un determinado tiempo el valor promedio del estado de opinión del grupo y la desviación estándar del conjunto de los estados de opinión de cada individuo Sj(t_d) en un tiempo dado t_d. La desviación estándar es una medida de la dispersión de los datos, indica cuánto se alejan estos del valor promedio; por tanto, si se alcanza el consenso, el valor de la desviación estándar sería nulo, y mientras mayor es la desviación estándar, más alejado estará el sistema del consenso. Se obtuvo la evolución de la desviación estándar para distintos tipos de muestras y lo que se observa es que el consenso se alcanza cuando la red es completa fa = 1; es decir, todos los nodos se hallan vinculados con todos los otros, al disminuir el valor de este parámetro también se aleja la muestra del consenso. Por otra parte, se obtuvo que al aumentar el tamaño de la muestra N, mayor es la tendencia al consenso. Entonces, podemos concluir que lo determinante para alcanzar el consenso es la homogeneidad de la red, solo cuando es completamente homogenea y fa = 1; es decir, cuando todos los individuos se hallan vinculados a todos los demás, el consenso es alcanzable. Por otra parte, el tamaño de la muestra N, es una variable que puede ayudar a disminuir la dispersión de las opiniones. Mientras mayor es el tamaño de la red menos dispersos resultan los estados de opinión de los individuos; es decir, se trata de una variable que contribuye a acercarnos al consenso cuando es grande.

 

5. LOS INTRANSIGENTES EN EL MODELO

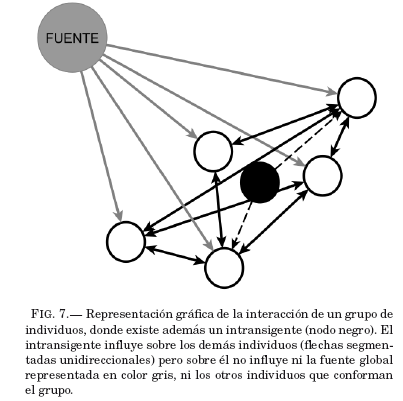
Se define como intransigente a un individuo que tiene una opinión definida de valor nulo y que permanece inalterable en el transcurso del tiempo, en acuerdo con la definición dada por Galam & Jacobs (2007). Estos individuos intransigentes no pueden ser influenciados por los demás individuos ni tampoco por la fuente global, su opinión permanece constante a cada paso del tiempo, no evoluciona; sin embargo, como forma parte de la sociedad, al interactuar con los otros individuos está opinión intransigente puede afectar al estado de opinión media de la red. En la Fig. 7 se representa la red con la presencia de un intransigente.

5.1. Efecto de los intransigentes en el caso de conectividad a la fuente constante

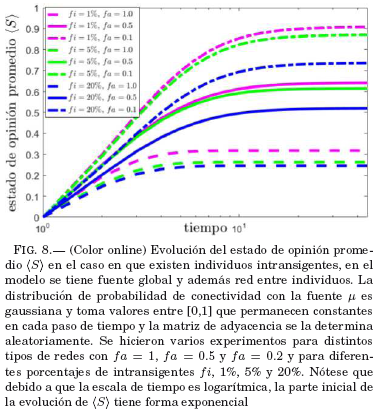
A continuacion se procede a analizar el efecto, en la evolución de estado de opinión promedio (S), con la introducción de individuos intransigentes en el modelo. Primero, se considera un modelo en el que la conectividad de los individuos a la fuente permanece constante. Para el análisis se toman distintas fracciones de intransigentes (en porcentaje) denotadas por fi en relación al número total de individuos y redes con distintos fa. Se procede a hacer el análisis sobre una muestra de 100 individuos. Se tienen estados de evolución promedio para tres distintas proporciones de intransigentes en la muestra: 1%, 5% y 20% correspondientes a las líneas magenta, verde y azul respectivamente como se muestra en la Fig. 8. A su vez, se aplicó a cada uno de estos casos, tres distintos tipos de red: fa = 1.0, fa = 0.5 y fa = 0.1 correspondientes a línea segmentada, continua y punto-segmento respectivamente. Nótese que las curvas de la Fig. 8, se comportan de la misma manera que las curvas de la Fig. 4, donde se estudiaba la evolución de (S) sin la existencia de intransigentes. La diferencia principal está en el alcance que se tiene de (S)_MAX, se puede ver que en general, el efecto de introducir individuos intransigentes disminuye el valor de (S)_MAX. En las curvas de la Fig. 4, cuando no existen intransigentes, para todos los tipos de muestras y grados de conectividad de la red se alcanzan valores mayores a 0.95 para el estado de opinión promedio máximo (S)_MAX La introducción de intransigentes hace que los valores para (S)_MAX sean considerablemente menores, llegando en algunos casos a ser menores a 0.3.

También se observa que el valor de (S)_Max alcanzado difiere según los casos analizados. Así, cuando la red es debilmente conectada (fa = 0.1, curva punto-segmento), se tienen los valores mayores de (S)_MAX; en contraposición, para una red homogénea, (fa = 1.0, curvas segmentadas), se tienen los valores menores de (S)_MAX .

Por otra parte,(S)_MAXdepende también de la presencia de intransigentes (caracterizada por el color de línea), pero en menor grado que de la conectividad de la red (caracterizada por el tipo de línea). Nótese que las curvas en magenta correspondientes a fi = 1% son las que alcanzan un valor mayor de (S)_MAX, mientras que las azules (fi = 20%, importante presencia de intransigentes) son las que tienen menores valores de (S)_MAX.

Por tanto, el número de intransigentes en el grupo, no es la variable determinante en el alcance de (S)_MAX, como se podría pensar intuitivamente. Lo importante es la combinación de este número con el tipo de red. Para una red con poca conectividad por muchos intransigentes que se tenga, el valor de (S)_MAX no se ve modificado de manera significativa; en cambio, si se tiene una red homogenea, aunque se tengan pocos intransigentes, el valor de (S)_MAX se reduce considerablemente.

Para estudiar como afecta la introducción de intransigentes en el consenso, como ya se explicó en la Sec. 4, analizamos la desviación estándar y se obtiene que cuando el número de intransigentes es mayor, también lo es la desviación estándar, es decir que se está más lejos del consenso; en cambio, cuanto menos intransigentes existen en la muestra, menor es la dispersión de las opiniones de los individuos o más cerca del consenso se está.

5.2. Efecto de los intransigentes en el caso de conectividad a la fuente variable

Para caracterizar la forma en como afectan los intransigentes, se realizan experimentos para ver su efecto sobre distintos tipos de muestras y con distintas fracciones de número de intransigentes en cada una de ellas.

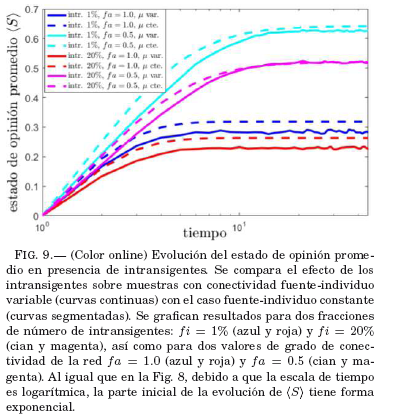
En la Fig. 9 comparamos el efecto de los intransigentes sobre muestras con conectividad fuente-individuo variable (curvas continuas) con el caso fuente-individuo constante (curvas segmentadas). Nótese que en todos los casos, para los distintos tipos de muestras se tiene que el efecto de intransigentes es mayor en las muestras con conectividad variable puesto que las curvas continuas siempre estan por debajo de las segmentadas del mismo color; es decir, disminuyen el valor de(S)_MAX aun más, en muestras con conectividad variable, de lo que lo hacen en las muestras de conectividad constante. Lo anterior resulta contraintuitivo ya que cuando la conectividad es variable, sin intransigentes se alcanza el máximo valor posible de (S)_MAX.

Por otra parte, se nota también que el efecto de los intransigentes es más importante en redes homogéneas, en las que fa = 1.0 (curvas azul y roja) pues estan más distantes de sus correspondientes curvas en línea segmentada, que en el caso de las muestras con redes con grado de conectividad menor fa = 0.5 (curvas cian y magenta). En estas últimas redes, las curvas cian y magenta de trazo continuo y las de trazo segmentado, estan casi sobrepuestas; es decir, el efecto de los intransigentes es menor.

Al igual que en la Sec. 5.1 el efecto de los intransigentes no depende solo de su número sino de la combinación de este con la conectividad.

Una de las principales diferencias entre los gráficos de conectividad variable (trazo continuo) con los de conectividad constante (trazo segmentado), es que en los primeros, se puede ver una fluctuacion en la parte de estabilización de (S)

El efecto principal de la presencia de intransigentes en las redes con conectividad fuente-individuo variable, es que la desviación estándar no se anula en ningún caso; en cambio, en las redes homogéneas de conectividad fuente-individuo constante, el valor de la desviación estándar se anula; es decir, se alcanza el consenso.

 

6. EVOLUCION DEL ESTADO DE OPINIÓN PROMEDIO CUANDO NO ACTUA UNA FUENTE DE EMISIÓN GLOBAL

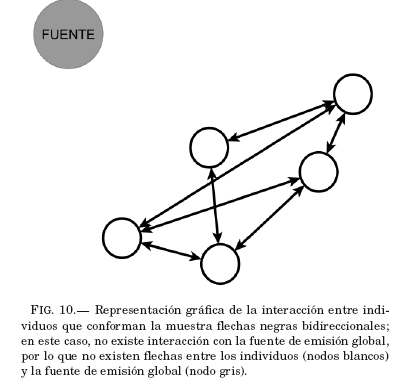
Se analiza la evolución del estado de opinión de un grupo de N individuos pero a diferencia de la Sec. 4, se considera está vez que la fuente global no actúa sobre los individuos. La interacción se da solo entre los individuos que conforman la red. En la Fig. 10, se hace una representación gráfica de está situación.

El modelo, para este caso queda expresado del siguiente modo

A diferencia de los anteriores casos (Secs. 3 y 4) la opinión inicial de todos los individuos no es cero, se realiza un sorteo para asignar opiniones iniciales a los mismos con valores en el intervalo [0,1], bajo una distribución gaussiana por lo que el promedio del valor del estado de opinión inicial del grupo es aproximadamente de 0.5.

Se realizan simulaciones para tres tamaños de muestras diferentes N = 50, N = 200 y N = 500.

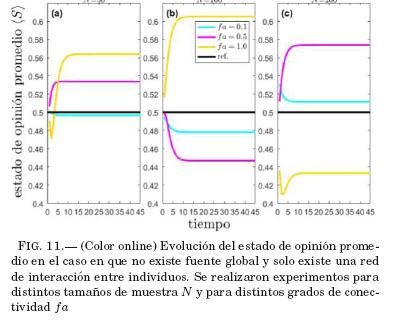
Para cada tamaño de muestra se consideran distintos valores de fa: 1.0, 0.5 y 0.1. En la Fig. 11, se dstinguen las curvas para cada valor de fa por el color de línea: naranja para fa = 1.0, magenta para fa = 0.5 y cian para fa = 0.1. Se puede ver que las curvas correspondientes a todos estos casos, presentan evoluciones muy diversas del estado de opinión promedio; por ejemplo, en algunos casos se tiene una evolución del estado de opinión promedio inicial creciente y en otros decreciente; sin embargo, al transcurrir el tiempo, en todos los casos se alcanza una situación de estabilización, en la que el estado de opinión promedio se mantiene constante. Este tiempo en el que se alcanza la estabilización está entre los 5 y 10 pasos. En la Sec. 4, donde se tenía además la acción de la fuente de emisión global, se obtuvieron tiempos de estabilización entre 10 y 15 pasos.

A diferencia del caso en el que actúa también la fuente de emision global, ahora no es importante el tamaño de la muestra N para la determinación del estado de opinión promedio. Sin embargo, el valor de fa, que es una característica de la red, afecta en la evolución del estado de opinión promedio: cuando fa es pequeño, el estado de opinión promedio casi no cambia, se mantiene muy cerca a su valor inicial (aproximadamente 0.5). A medida que el valor de fa se acerca a 1.0, el estado de opinión promedio evoluciona alejandose cada vez más del valor inicial promedio, véase las curvas de la Fig. 11, donde la línea negra horizontal en el valor de 0.5 (estado de opinión promedio inicial aproximado y usado como referencia) permite ver como los estados de opinión promedio en el equilibrio resultan más alejados del valor de referencia cuando fa es mayor.

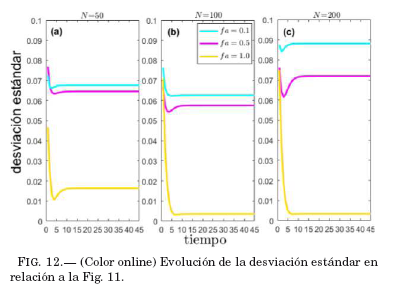
El valor de fa que caracteriza la red, también es muy importante en la dispersión de las opiniones de los individuos que conforman la red como se muestra en la Fig. 12. A medida que el valor de fa aumenta, la dispersión de las opiniones disminuye; sin embargo, no se alcanza el consenso porque en ningún caso el valor de la desviación estándar se anula, pero tiende a hacerlo cuando fa toma el valor de 1.0. Nótese que si bien los valores de (S)se estabilizan, esto no implica que todos los agentes tengan la misma opinión; es decir, este hecho no garantiza consenso. Por otro lado, si la desviación estándar se aproxima a cero o tiende a cero, como en el caso de la curvas correspondientes a fa = 1.0 en la Fig. 12, podemos decir que existe una tendencia al consenso. Para aclarar más el concepto de consenso que utilizamos, observemos en la Fig. 11 que todas las curvas se estabilizan después de un cierto tiempo pero solo la curva correspondiente a la situación con fa = 1.0 tiende a tener una desviación estándar pequeña, lo que no ocurre con las curvas correspondientes a fa = 0.1 y fa = 0.5. Sin importar el valor que adquiera (S), se tendra consenso si su desviación estándar correspondiente tiende a cero.

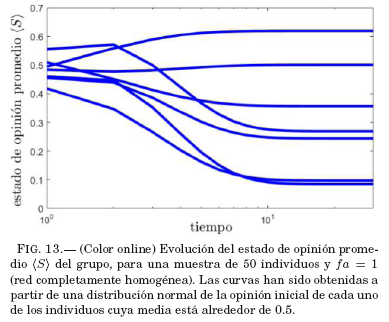
A continuacion se muestra cómo influyen las condiciones iniciales de cada individuo en la evolución de la opinión promedio. Para ello se fijan los valores: N = 50, fa = 1 (red completamente homogenea), haciéndose variar la opinión inicial de cada individuo, siendo que estas estan normalmente distribuidas con medias alrededor de 0.5 como se muestra en la Fig. 13, notándose que aún cuando los valores promedios de la opinión inicial son muy próximos, la evolución del estado de opinión promedio puede ser muy diferente de un experimento a otro, lo que indica una sensibilidad a las condiciones iniciales de las opiniones individuales.

 

7. CONCLUSIONES Y PERSPECTIVAS

Se hizo el análisis de la evolución del estado de opinión de un grupo de individuos basado en un modelo discreto. Se analizaron cuatro casos para este modelo.

El primer caso corresponde a la situación en el que solo existe acción de una fuente global sobre los individuos. Se estudiaron los casos en que la conectividad a la fuente es binaria, es decir que toma solo los valores discretos 0 o 1; o continua, en la que toma valores continuos en el intervalo entre 0 y 1, tomándose para cada caso las variantes constante o variable en el tiempo. Se obtuvo que no hay grandes diferencias entre los casos desarrollados, la diferencia principal, se da entre la situación de si la conectividad es constante o variable en el tiempo. Para la situación de conectividad variable, se tiene que el valor de estado de opinión promedio máximo alcanzado (S)_MAX es la unidad, con o sin red. Para conectividad constante, el valor alcanzado, es menor a la unidad. Las otras variantes de la conectividad fuente-individuo (discreta o continua, de distribución uniforme o gaussiana), dan lugar al mismo comportamiento al introducir la red. Consecuentemente, no es relevante cual se escoja; sin embargo, la distribución gaussiana tanto para la conectividad fuente-individuo como para la red puede considerarse la situación más proxima a la realidad.

Como segundo caso, se considero que además de la acción de la fuente de emisión global sobre los individuos, existe interacción entre los mismos mediante una red. Cuando se introduce la red, su efecto en una primera etapa es de ralentizar la evolución de opinión promedio, pero durante la segunda etapa más bien es el de contribuir a alcanzar una opinión promedio, mayor a la que se obtendría sin red. Lo anterior sucede independientemente del tipo de conectividad que exista entre los individuos y la fuente. Un segundo aspecto consistio en caracterizar este modelo realizando varios experimentos para distintos tamaños de muestras N y de grado de conectividad de la red fa. La importancia del grado de la red fa se manifiesta en el hecho de que presenta una proporcionalidad inversa con el estado de opinión promedio. Durante la segunda etapa, la variable fa deja de ser relevante y es más bien el tamaño de la muestra N el que determina el valor de opinión promedio máximo, de manera directamente proporcional. Cuando se tienen muestras muy grandes, el estado de opinión promedio tiende a 1, independientemente del grado de conexión de la red fa. Cuando las muestras son pequeñas no necesariamente se alcanza la unidad y el valor depende del grado conectividad de la red fa. Este efecto de añadir red es el mismo independientemente del tipo de conexión con la fuente. Un tercer aspecto, fue analizar el consenso y se encontro que el mismo siempre es alcanzado cuando fa = 1; además, mientras mayor es el tamaño de la red menor es la dispersión de las opiniones.

Como tercer caso, se considero la introducción de individuos intransigentes en la muestra que tiene como efecto el de disminuir la opinión promedio maxima alcanzada. Se obtuvo que el efecto de los intransigentes no depende fuertemente de su número o fraccion, sino del grado de conectividad de la red fa, dependiendo de una manera directamente proporcional. La variabilidad de la conectividad a la fuente magnifica el efecto de los intransigentes, produciendo además una fluctuación en la opinión promedio maxima. La presencia de intransigentes provoca dispersión de las opiniones y alejamiento del consenso

Para el cuarto caso, se considero que solamente existe red de individuos, observandose que el tamaño de la muestra N deja de ser relevante para el alcance del estado de opinión promedio de la estabilización; en contraposición, el grado de conectividad fa juega un rol importante, cuando es signficativamente grande, provocando cambios drásticos en los valores de opinión promedio, cuando este es pequeño casi no existe evolución del estado de opinión promedio. Un resultado muy importante es la sensibilidad a las condiciones iniciales (en las opiniones individuales) para la evolución del estado de opinión promedio (S) que se manifiesta cuando se fijan los valores de N y fa. Este último resultado es muy importante pues es la rúbrica de un comportamiento no lineal que además permite pensar en la obtención de las cuencas de atracción y en posibles situaciones de control con base en el conocimiento de estas.

Este estudio puede ser ampliado considerando otro tipo de individuos tales como los denominados contrarios, los cuales son agentes que adoptan siempre una posición opuesta a la de la mayoría, cualquiera fuere está, como lo especifica Galam (2004) o con los denominados agentes flotantes que cambian su opinión para que está sea acorde con la de la mayoría.

 

AGRADECIMIENTOS

Agradecemos a la Carrera de Física y al Instituto de Investigaciones Físicas por habernos permitido desarrollar está investigación en las mejores condiciones.

Conflicto de intereses

Los autores declaran que no hay conflicto de intereses con respecto a la publicación de éste documento.

 

REFERENCIAS

Milgram S. (1967), Psychology Today 1, 61.         [ Links ]

Travers J. & Milgram S. (1969), Sociometry 321, 425.         [ Links ]

Watts D. J. & Strogatz S. H. (1998), Nature 393, 440.         [ Links ]

Granovetter M. & Soong R. (1978), The Journal of Mathematical Sociology 9, 165.         [ Links ]

Bavelas A. (1948), Human Organization 7, 16.         [ Links ]

Freeman L. (1978), Social Networks 1, 215.         [ Links ]

Freeman L., Roeder D. & Mullholland R. R. (1979), Social Networks 2, 119.         [ Links ]

Castellano C., Fortunato S. & Vittorio L. (2009), Review of Modern

Physics 81, 591. Weidlich W. & Haah G. (1983), Concepts and models of a quantitative sociology. (New York: Springer Verlag)         [ Links ]

Freeman L. (2004), The development of social network analysis. (Vancouver: Empiracl Press)        [ Links ]

Helbing D. (2010), Quantitative sociodynamics: stochastic methods and models of social interaction processes. (Berlin: Springer)         [ Links ]

Newman M. E. J. (2004), The European Physical Journal B 38, 321.         [ Links ]

Newman M., Barabasi A. L. & Watts D. J. (eds.) (2006), The structure and dynamics of networks. (Princeton: Princeton University Press)        [ Links ]

Barabasi A. L. & Albert R. (1999), Science 286, 509.         [ Links ]

Strogatz S. H. (2001), Nature 410, 268.         [ Links ]

Arenas A., Díaz-Guilera A., Kurths J., Moreno Y. & Zhou C. (2008), Physics Reports 469, 93.         [ Links ]

Wu C. W. (2007), Synchronization in complex networks of non linear dynamical systems (Londres: World Scientific Publishing)        [ Links ]

Lu X. B. & Qin B. Z. (2011), Synchronization in complex networks (Nueva York: Nova Science Pub. Inc)        [ Links ]

Boccaletti S., Latora V., Moreno Y, Cliavez M. & Hwang D. U. (2006), Physics Reports 424, 175.         [ Links ]

Estrada E. (2011), The structure of complex networks: theory and applications (Oxford: University Press)        [ Links ]

Barrat A., Barthelemy M. & Vespignani A. (2011), Dynamical processes on complex networks (Cambridge: Cambridge University Press)        [ Links ]

Barabasi A. L. (2002), Link the new science of networks (Cambridge: Perseus Publishing)        [ Links ]

Caldarelli G. & Catanzaro M. (2012), Networks: a very short introduction (Oxford: Oxford University Press)        [ Links ]

Bassett D., Alderson D. L. & Carlson J. M. (2012), Physical Review E 86, 36105.         [ Links ]

Erdos P. & Rényi A. (1960), Publications of the Mathematical Institute of the Hungarian Academy of Sciences 5, 17.         [ Links ]

Galam S. & Jacobs F. (2007), Physica A 381, 366.         [ Links ]

Galam S. (2004), Physica A 333, 453.         [ Links ]