Services on Demand
Journal
Article
Indicators
Related links
Share
Revista Boliviana de Física
On-line version ISSN 1562-3823
Revista Boliviana de Física vol.30 no.30 La Paz Nov. 2017
ARTÍCULOS
Sincronización de neuronas modeladas por mapas y caracterizadas por periodicidades
Synchronization of map modeled neurons and characterized by periodicities
Ignacio Calderón de la Barca* & Gonzalo Marcelo Ramírez-Ávila†
†Instituto de investigaciones Físicas, Carrera de Física Universidad Mayor de San Andres c. 27 Cota-Cota, Campus Universitario, Casilla de Correos 8639 La Paz - Bolivia
*icalderon@fiumsa.edu.bo
†mravila@fiumsa.edu bo
http://www.fiumsa.edu.bo/docentes/mramirez/
(Recibido 22 de agosto de 2017; aceptado 27 de septiembre de 2017)
Resumen
Se estudia la sincronización de dos neuronas acopladas eléctricamente en función de la intensidad de acoplamiento y periodicidad que las caracteriza, empleando como indicador el error medio de sincronización. La actividad neuronal presenta dos dinámicas: una rápida en la cual se producen impulsos de los potenciales de acción y otra lenta que los modula, produciendo como resultado un comportamiento de gran importancia fisiológica denominado ráfagas de picos. Estos comportamientos intrínsecos de las neuronas estan bien caracterizados en el plano de parámetros por periodicidades. Se ha encontrado que valores altos de la intensidad de acoplamiento llevan al sistema a perder regularidad en sus oscilaciones, por lo que se limita el intervalo de análisis. Asi, se observa que se alcanza una sincronización completa solamente entre neuronas idénticas acopladas; mientras que en otras situaciones, se manifiesta una sincronización en fase. Además, en el caso de neuronas de igual periodicidad, la serie temporal del error medio de sincronización muestra oscilaciones periódicas y con periodicidades similares a las señales neuronales.
Codigo(s) PACS: 05.45.-a 05.45.Xt 02.70.-c 87.19.L-
Descriptores: Dinámica no lineal y caos Sincronización; osciladores acoplados Técnicas computacionales; simulación Neurociencia.
Abstract
We studied the synchronization of two electrically coupled neurons as a function of the coupling strength and their characteristic periodicities, using as an indicator the mean synchronization error. The neural activity presents two dynamical features: a fast one in which impulses are produced from the action potentials and a slow one that modulates them; together these result in a behavior of great physiological importance here called bursts of spikes. These intrinsic neural behaviors are well characterized by periodicities in the parameter plane. We found that high coupling strength values provoke a loss of regularity in the oscillations which delimit the interval analysis. Thus, we observed that complete synchronization is only achieved when coupled neurons are identical, whereas in other situations phase synchronization is manifested. Moreover, in the case of non-identical coupled neurons with the same periodicity, the time series of the mean synchronization error exhibit periodic oscillations with similar periodicities of the neuron's signals.
Subject headings: Nonlinear dynamics and chaos Synchronization; coupled oscillators Computational techniques; simulation Neuroscience.
1. INTRODUCCIÓN
El estudio de redes complejas se ha extendido ampliamente en las últimas décadas y está relacionado con múltiples disciplinas científicas, como ser la neurociencia. Responsables del procesamiento de información y de la ejecución de actividades funciónales las redes neuronales son específicas a ciertas regiones y funciones como lo señalan Azevedo et al. - (2009) A grandes rasgos se distinguen tres partes en una neurona: las dendritas, la terminal de axón (ambas terminaciones nerviosas) y una membrana conductora llamada axón. Para que una colección de estas células procese información las mismas deberán conectarse, este es el proceso conocido como sinápsis y sucede cuando se aproximan las terminaciones nerviosas del axón con las dentritas, transfiriéndose una señal electroquímica, comúnmente una corriente iónica. Dicha señal se conduce a través de las neuronas receptoras a causa de una diferencia de potencial eléctrico entre los extremos del axón y sus terminales, producida por la diferencia de concentración de iones en la frontera de la membrana como se describe en Girardi et al. (2013). Formalmente, tal conducción está ligada con lo que se conoce como potenciales de acción. Cada tipo de neurona posee un umbral de excitación característico, el cual debe ser superado para permitir un potencial de acción, esto fue reportado por primera vez por Hodgkin & Huxley (1952).
Desde los trabajos experimentales con redes neuronales artificiales desarrollados por Sarbadhikari & Chakrabarty (2001), se sabe que la dinámica neuronal puede presentar comportamientos periódicos y caóticos. Las oscilaciones periódicas se manifiestan en dos procesos: la descarga de iones en el axón que ocurre rápidamente y en repetidas ocasiones, y el alcance de valores umbral de excitación que modulan el tiempo de conducción. Los comportamientos intrínsecos de las neuronas son: oscilaciones sostenidas, ráfagas de impulsos o picos, oscilaciones caóticas y silencio o ausencia de oscilaciones. Adicionalmente a los mecanismos mencionados anteriormente, se puede considerar una red neuronal como un sistema de entrada y salida (input/output) conformado por osciladores; es decir, un sistema al que ingresa una señal y del que sale otra diferente. Tales aspectos posibilitan el estudio de redes neuronales con la dinámica no lineal.
A partir de observaciones fisiológicas, en el trabajo de Hodgkin & Huxley (1952) se propuso un modelo de ecuaciones en derivadas parciales, siendo pioneros en abordar una descripción matemática del comportamiento neuronal. Posteriores trabajos realizados por FitzHugh (1955), Nagumo et al. (1962), Hindmarsh & Rose (1984) e Izhikevich (2003), redujeron el sistema anteriormente mencionado a variantes mas sencillas como se muestra en Girardi et al. (2013). Adaptaciones de los modelos basados en ecuaciones diferenciales ordinarias y/o en derivadas parciales, permitieron discretizar las ecuaciones, lo que constituye una simplificación importante. Estos nuevos sistemas con tiempos discretos, llamados mapas, presentan ventajas teóricas por tener formas matemáticas más sencillas y seguir mostrando los comportamientos dinámicos de relevancia, como se expone en Ibarz et al. (2011).
Las simulaciones computacionales constituyen la herramienta ideal para estudiar los comportamientos oscilatorios de las neuronas. En las ultimas decadas se han desarrollado varios modelos que exhiben comportamientos oscilatorios observables en neuronas reales, tales como: ráfagas de impulsos o picos o mas conocidas como "bursts of spikes" en la literatura en ingles, que son trenes de impulsos seguidos de desexcitaciones y excitaciones; oscilaciones sostenidas o "spikes", que son impulsos con cierto período; silencio, que es un estado estacionario caracterizado dinámicamente por puntos fijos y por último, oscilaciones caóticas.
Uno de los propósitos más importantes de los modelos basados en mapas es el de entender los mecanismos que subyacen en el procesamiento de información y actividades funciónales de las neuronas. Estudiar la sincronización de una red entre varias de estas subregiones es relevante por que aporta al conocimiento de codificación y procesamiento de información en neuronas, estrechamente relacionado con la memoria a corto plazo como se expone en Sausedo-Solorio & Pisarchik (2014).
El comportamiento síncrono de ráfagas de impulsos esta relacionado con ciertas patologías como lo indican de Pontes et al. (2008), por lo que su estudio es de suma importancia como lo plantea Rulkov (2001). La gran mayoría de trabajos se enfocan en redes neuronales con conexiónes que cumplen la propiedad de escalamiento libre, donde el acoplamiento se reduce mientras incrementa el tamaño de la red según una ley de potencias como lo señalan Batista et al. (2009), de Pontes et al. (2008) y considerando un retardo sináptico entre las señales estudiado por Sausedo-Solorio & Pisarchik (2014).
El artículo está estructurado de la siguiente manera: en la Sección 2. se introduce todas las propiedades y aspectos concernientes al análisis del modelo que se emplea. La Sección 3. muestra los resultados más importantes entre los que destacan la dependencia del error de sincronización con la intensidad de acoplamiento y la serie temporal del mismo para neuronas que presentan comportamientos diferentes. Finalmente, en la Sección 4. se exponen las conclusiones del trabajo, así como perspectivas para posibles extensiones de la investigación.
2. MODELO DE RULKOV
La forma matemática del modelo de neurona de Rulkov es sencilla; sin embargo, este es capaz de describir diversidad de comportamientos, incluyendo los cuatro mencionados en la Sección 1. Modelar neuronas que presentan el comportamiento de ráfagas de impulsos implica la dinámica de dos variables, una de ellas, y cambia su valor lentamente con el tiempo discreto n y modula el período de otra variable, x que produce ráfagas de impulsos. El mapa bidimensional planteado por Rulkov (2002) esta dado por

Varios de los parámetros tienen una relación directa con aspectos biológicos, ![]() representan influencias externas (interacción con otras neuronas) correspondientes a la sinápsis y conducción respectivamente. En tanto que a es un parámetro característico de cada neurona aislada, relacionado con los potenciales de acción y el desplazamiento vertical del umbral de excitación en el plano de parámetros; mientras que a repolariza la membrana, delimitando los comportamientos de impulsos y ráfagas. Finalmente, el parametro
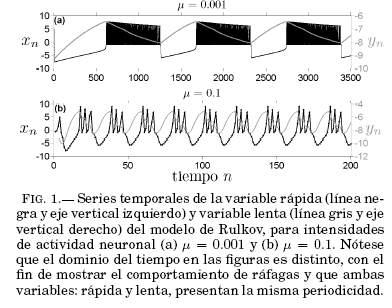
representan influencias externas (interacción con otras neuronas) correspondientes a la sinápsis y conducción respectivamente. En tanto que a es un parámetro característico de cada neurona aislada, relacionado con los potenciales de acción y el desplazamiento vertical del umbral de excitación en el plano de parámetros; mientras que a repolariza la membrana, delimitando los comportamientos de impulsos y ráfagas. Finalmente, el parametro ![]() esta relacionado con la intensidad de actividad; es decir, mientras mayor sea su valor, mas frecuente sera la actividad neuronal. La Fig. 1 muestra las series temporales de las variables rapida y lenta en un comportamiento de ráfagas de picos para valores de
esta relacionado con la intensidad de actividad; es decir, mientras mayor sea su valor, mas frecuente sera la actividad neuronal. La Fig. 1 muestra las series temporales de las variables rapida y lenta en un comportamiento de ráfagas de picos para valores de ![]() = 0.001 y
= 0.001 y ![]() = 0.1. En las dos situaciones puede observarse que ambas variables comparten periodicidad. Como consecuencia del valor de la intensidad de actividad, notese que la escala temporal para la Fig. 1(b) es menor y a pesar de ello se tienen mas trenes de ráfagas, pero con mucha menor cantidad de picos que en la Fig. 1(a).
= 0.1. En las dos situaciones puede observarse que ambas variables comparten periodicidad. Como consecuencia del valor de la intensidad de actividad, notese que la escala temporal para la Fig. 1(b) es menor y a pesar de ello se tienen mas trenes de ráfagas, pero con mucha menor cantidad de picos que en la Fig. 1(a).
2.1. Caracterización mediante periodicidades
Los comportamientos neuronales quedan caracterizados en un plano de parámetros, para ![]() , en el cual se distinguen tres regiones bien definidas correspondientes al silencio (puntos fijos), ráfagas de impulsos y oscilaciones sostenidas, tal como lo introdujo Rulkov (2002). Por otra parte la caracterización de mapas mediante periodicidades muestra ser un método alternativo al empleo de exponentes de Lyapunov siendo mas ventajoso en el sentido que describe con mayor detalle las dinámicas oscilatorias de los sistemas, como se reporta en Ramírez-Avila & Gallas (2011). También utilizando éste metodo, se obtiene un plano de parámetros extendido para el mapa de Rulkov caracterizado por periodicidades, modelado para un valor no tradicional de intensidad de actividad
, en el cual se distinguen tres regiones bien definidas correspondientes al silencio (puntos fijos), ráfagas de impulsos y oscilaciones sostenidas, tal como lo introdujo Rulkov (2002). Por otra parte la caracterización de mapas mediante periodicidades muestra ser un método alternativo al empleo de exponentes de Lyapunov siendo mas ventajoso en el sentido que describe con mayor detalle las dinámicas oscilatorias de los sistemas, como se reporta en Ramírez-Avila & Gallas (2011). También utilizando éste metodo, se obtiene un plano de parámetros extendido para el mapa de Rulkov caracterizado por periodicidades, modelado para un valor no tradicional de intensidad de actividad ![]() = 0.1 estudiado por Ramírez-Ávila et al. (2015). Aqui, cabe resaltar que todos los trabajos mencionados se han dedicado a estudiar sincronización de neuronas caracterizadas solamente por su comportamiento de ráfagas para un valor de uno de los parámetros, dado por
= 0.1 estudiado por Ramírez-Ávila et al. (2015). Aqui, cabe resaltar que todos los trabajos mencionados se han dedicado a estudiar sincronización de neuronas caracterizadas solamente por su comportamiento de ráfagas para un valor de uno de los parámetros, dado por ![]() = 0.001. El presente trabajo tiene como objetivo estudiar la sincronización de dos neuronas caracterizadas por periodicidades para un valor de
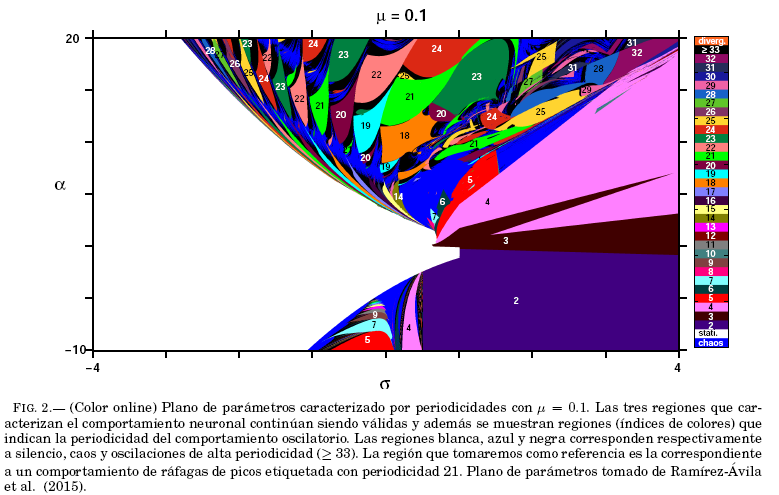
= 0.001. El presente trabajo tiene como objetivo estudiar la sincronización de dos neuronas caracterizadas por periodicidades para un valor de ![]() = 0.1, haciendo una seleccion de: neuronas idénticas, que comparten periodicidad y de otras que difieren en periodicidad y comportamiento. Volviendo al plano de parámetros, se muestra el mismo en la Fig. 2, observandose una gran riqueza de comportamientos dinámicos (múltiples regiones). El código de colores indica la periodicidad en las diferentes regiones del plano, correspondiendo además la región blanca y la mas oscura al silencio y caos respectivamente. Para los análisis que siguen, elegimos como referencia una neurona en la region de periodicidad 21, caracterizada por
= 0.1, haciendo una seleccion de: neuronas idénticas, que comparten periodicidad y de otras que difieren en periodicidad y comportamiento. Volviendo al plano de parámetros, se muestra el mismo en la Fig. 2, observandose una gran riqueza de comportamientos dinámicos (múltiples regiones). El código de colores indica la periodicidad en las diferentes regiones del plano, correspondiendo además la región blanca y la mas oscura al silencio y caos respectivamente. Para los análisis que siguen, elegimos como referencia una neurona en la region de periodicidad 21, caracterizada por ![]() = 14.13 y
= 14.13 y ![]() = 0.3622.
= 0.3622.
2.2. Indicadores de sincronización
Como consecuencia de la interacción de elementos en un sistema complejo compuesto de osciladores, se puede producir la sincronización, fenómeno emergente omnipresente en la naturaleza en diversidad de ciencias. Este fenómeno puede surgir abruptamente en una red compleja, como reporta Boccaletti et al. (2016). Se pueden distinguir diferentes tipos de sincronización tales como la sincronización completa, en fase, generalizada, con retardo, entre otras, como lo señala Ramírez-Ávila (2007). Para estudiar la sincronización empleamos dos cantidades: (i) El error medio de sincronización que se define como la distancia promedio a la variedad de sincronización, lo cual implica que las diferencias de las variables para cada oscilador en cada tiempo n sean nulas o proximas a cero; en otras palabras, que la distancia euclidiana entre las señales de los osciladores sean proximas a cero en el caso de la sincronización
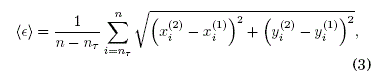
donde nT es un transitorio. (ii) El error máximo que es el maximo valor de las distancias euclideanas para los n - nT valores
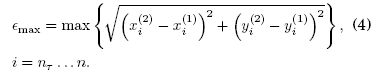
2.3. Acoplamiento
La interacción sináptica de dos neuronas requiere una conexión entre los mapas que describen a las mismas. El acoplamiento víncula a los elementos de la red mediante interacciones. Dado que estamos interesados en estudiar las interacciones entre dos neuronas empleamos un acoplamiento bidireccional, simétrico y de carácter eléctrico como se expone en Girardi et al. (2013)
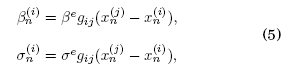
donde ![]() son cantidades correspondientes a la intensidad de la sinápsis entre neuronas y la magnitud del potencial de acción de entrada, como se explicó previamente. La cantidad gij es una matriz simétrica y de diagonal nula que define la conexión entre neuronas. En lo que sigue del trabajo, nos referiremos a la magnitud de los elementos de dicha matriz como la intensidad de acoplamiento g.
son cantidades correspondientes a la intensidad de la sinápsis entre neuronas y la magnitud del potencial de acción de entrada, como se explicó previamente. La cantidad gij es una matriz simétrica y de diagonal nula que define la conexión entre neuronas. En lo que sigue del trabajo, nos referiremos a la magnitud de los elementos de dicha matriz como la intensidad de acoplamiento g.
3. RESULTADOS
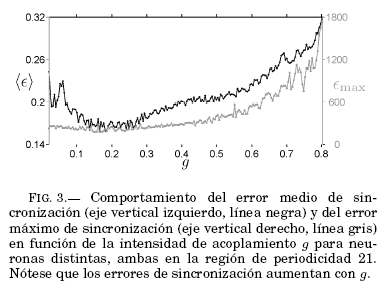
Con el objetivo de observar el efecto de la intensidad de acoplamiento en el comportamiento oscilatorio de las neuronas, analizamos los errores de sincronización, dados por las ecuaciones (3) y (4) en función de la intensidad de acoplamiento. Se estudió la interacción de dos neuronas distintas que comparten periodicidad, incrementando el valor de la intensidad de acoplamiento g en un amplio rango de valores, como se muestra en la Fig. 3. Se observa que si el valor de la intensidad de acoplamiento es alto (próximo a g = 1.0), entonces el comportamiento inicial pierde regularidad en el período. En consecuencia, se debe limitar el intervalo de valores de g para los cuales los errores de sincronización son pequeños.
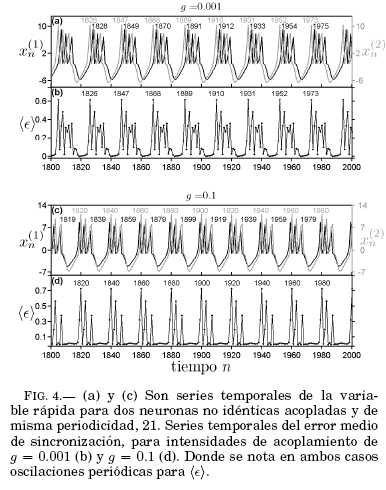
El análisis de las series temporales del error de sincronización para neuronas distintas que comparten periodicidad y para un valor específico del acoplamiento (g = 0.43) se muestran en la Fig. 4. Podemos apreciar las series temporales de ambas neuronas no idénticas acopladas con una intensidad de g = 0.001 Fig. 4(a) donde oscilan con la misma periodicidad y g = 0.1 Fig. 4(c), donde la periodicidad de una de las señales cambia ligeramente debido a un mayor acoplamiento. En ninguno de los casos las señales se superponen. El error medio de sincronización en función del tiempo, Fig. 4(b), presenta oscilaciones periodicas que comparten la periodicidad de las ráfagas que es 21, en concordancia con los resultados obtenidos por Bustos & Ramírez-Avila (2016) para un mapa unidimensional. En tanto que en la Fig. 4(d) se observa que las oscilaciones del error medio de sincronización cambian su periodicidad a 20. Estos comportamientos son una correspondencia de la naturaleza oscilatoria del fenómeno.
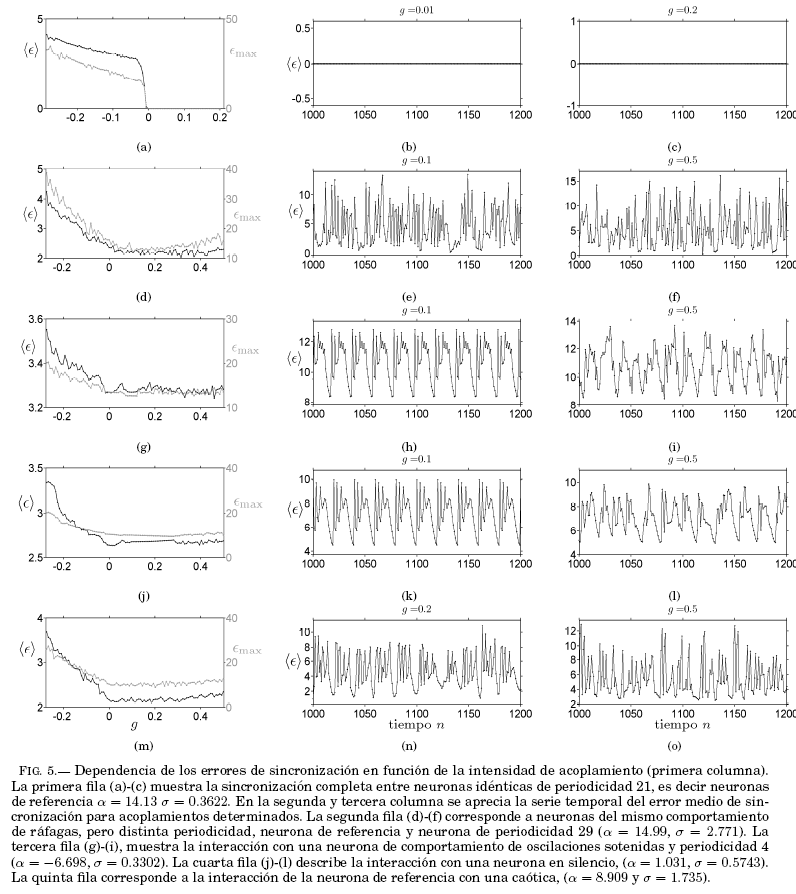
Finalmente, la Fig. 5, muestra la interacción de la neurona de referencia (![]() = 14.13,
= 14.13, ![]() = 0.3622) con otras neuronas distintas en comportamiento y periodicidad, como se especifica en la leyenda de la figura. Se puede ver que, a excepción de neuronas idénticas, en ningun caso se consigue una sincronización completa, pero sí se manifiesta una sincronización en fase para los casos: (i) cuando la neurona de referencia interactúa con otra que presenta ráfagas (ver Fig. 4), (ii) otra en su estado estacionario (ver Fig. 4) y (iii) una interacción con una neurona caótica (ver Fig. 4). Sin embargo, el período de
= 0.3622) con otras neuronas distintas en comportamiento y periodicidad, como se especifica en la leyenda de la figura. Se puede ver que, a excepción de neuronas idénticas, en ningun caso se consigue una sincronización completa, pero sí se manifiesta una sincronización en fase para los casos: (i) cuando la neurona de referencia interactúa con otra que presenta ráfagas (ver Fig. 4), (ii) otra en su estado estacionario (ver Fig. 4) y (iii) una interacción con una neurona caótica (ver Fig. 4). Sin embargo, el período de ![]() es sensible a cambios de la intensidad de acoplamiento, pese a que esta se encuentre en el intervalo de análisis.
es sensible a cambios de la intensidad de acoplamiento, pese a que esta se encuentre en el intervalo de análisis.
4. CONCLUSIONES Y PERSPECTIVAS
Se profundizo el estudio de las características dinámicas del modelo de Rulkov, tomando en cuenta valores de los parámetros que no se consideran comunmente pero que tienen una gran riqueza a nivel de comportamiento dinamico sobre todo en lo concerniente a periodicidades. Teniendo en cuenta una neurona de referencia en la región de periodicidad 21, se vio que la sincronización completa solo se presenta con otra neurona identica. Sin embargo, la sincronización en fase con otras neuronas que comparten periodicidad es posible y además, se observó que el error de sincronización oscila periódicamente en el tiempo y con periodicidades similares que los trenes de ráfagas de picos. Este comportamiento está en correspondencia con el caracter oscilatorio de las variables dinámicas del modelo. Con respecto a la interacción de la neurona de referencia y otra de periodicidad 4 (oscilaciones sostenidas) no presentan periodicidad, posiblemente debido a que se tiene una importante diferencia en la periodicidad además que la periodicidad de la serie temporal del error medio de sincronización puede desaparecer dependiendo del valor de acoplamiento.
Como perspectivas se pretende extender la investigación y estudiar más exhaustivamente la sincronización en fase y así caracterizar de manera mas general el comportamiento del error de sincronización en función de la intensidad de acoplamiento, pudiéndose construir un espacio de parámetros en términos de diferencias de ![]() Por ultimo es deseable a corto plazo extender este estudio a sistemas con mayor número de neuronas.
Por ultimo es deseable a corto plazo extender este estudio a sistemas con mayor número de neuronas.
REFERENCIAS
Azevedo, F.A.C., Carvalho, L.R.B., Grinberg, L.T., Farfel, J.M., Ferretti, R.E.L., Leite, R.E.P., Filho, W.J., Lent, R., Herculano- Howzel, S. (2009), Journal ofComparative Neurology 513, 532. [ Links ]
Batista, C.A.S., Batista, A.M., de Pontes, J.C.A., Lopes, S.R., &
Viana, R.L. (2009), Chaos, Solitons & Fractals 41, 2220. Batista, C.A.S., Lopes, S.R., Viana, R.L., & Batista, A.M. (2010),
Neural Networks 23, 114. Boccaletti, S., Almendral, J.A., Guan, S., Leyva, I., Liu, Z., Sendia-
Nadal, I., Wang, Z. and Zou, Y. (2016), Physics Reports 660, 1. Bustos, R.O.E. & Ramírez-Ávila, G.M. (2016), European Physical
Journal Special Topics 225, 2697. de Pontes, J.C.A., Viana, R.L., Lopes, S.R., Batista, C.A.S. &
Batista, A.M. (2008), Physica A 387, 4417. FitzHugh, R. (1955), The Bulletin of Mathematical Biophysics 17, 257.
Girardi, S.M., Tragtenberg, M.H.R. & Kinouchi, O. (2013), Journal of Neuroscience Methods 220, 116.
Hindmarsh, J.L. & Rose, R.M. (1984), Proceedings of the Royal Society of London B 221, 87.
Hodgkin, A.L. & Huxley, A.F. (1952), The Journal of Physiology 117, 500.
Ibarz, B, Casado, J.M. & Sanjuan, M.A.F. (2011), Physics Reports 501, 1.
Izhikevich, E.M. (2003), IEEE Transactions on Neural Networks 14, 1569.
Izhikevich, E.M. & Hoppensteadt, F. (2004), International Journal of Bifurcation and Chaos 14, 3847.
Nagumo, J., Arimoto, S. & Yoshizawa, S. (1962), Proceedings of the IRE 50, 2061.
Pecora, L.M. & Carroll, T.L (1990), Physical Review Letters 64, 821.
Ramírez-Avila, G.M. (2007), Revista Boliviana de Educación Superior en Ciencias 7, 25.
Ramírez-Ávila, G.M. & Gallas, J.A. (2011), Revista Boliviana de Física 19, 1.
Ramírez-Ávila, G.M., Gallas, M.R. & Gallas, J.A. (2015), Revista Boliviana de Física 27, 1.
Rulkov, N.F. (2001), Physical Review Letters 86, 183. Rulkov, N.F. (2002), Physical Review E 65, 041922.
Sarbadhikari, S.N. & Chakrabarty, K. (2001), Medical Engineering & Physics 23, 447.
Sausedo-Solorio, J.M. & Pisarchik, A.N. (2014), Physics Letters A 378,2108.
Schiff, S.J., Jerger, K., Duong, D.H., Chang, T., Spano, M.L., Ditto, W.L. & et al. (1994), Nature 370, 615.
Suykens, J., Yalcm, M. & Vandewalle, J. (2003), Chaos Control (New York: Springer), 117.