Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista Boliviana de Física
On-line version ISSN 1562-3823
Revista Boliviana de Física vol.29 no.29 La Paz Dec. 2016
ARTÍCULOS
Solución de ecuaciones diferenciales parciales con condiciones de contorno abiertas por el método de Monte Carlo
Solution of partial differential equations with open boundary conditions by the Monte Carlo method
V. Franz Suxo Mamani1"
email: fsuxo@fiumsa.edu.bo
(Recibido 17 de junio de 2016; aceptado 15 de diciembre de 2016)
Resumen
El metodo estocástico de Monte Carlo se aplica para resolver ecuaciones diferenciales parciales que tienen condiciones de contorno abiertas, es decir, ecuaciones cuyo dominio de solucion es infinito. Aplicamos este método a la ecuación de Laplace y a la ecuación de difusion, las cuales modelan fenómenos estacionarios y fenómenos de evolución temporal respectivamente, que son de mucho interes en la física. Como un primer paso se comprueba la eficacia del metodo de Monte Carlo al comparar los resultados numéricos con las soluciones analíticas de problemas conocidos. El siguiente paso fue aplicar el metodo a problemas físicos mas complejos que no tienen solución analítica. Encontramos que en el caso de la ecuacion de difusion, el método de Monte Carlo se aplica directamente sobre el dominio infinito del problema, mientras que en los metodos numéricos más comunes se requiere acotar el dominio del problema.
Codigo(s) PACS: 02.70.C 02.70.Bf 02.70.Uu
Descriptores: Tecnicas computacionales y simulaciones Método de diferencias finitas Aplicaciones de metodos de Monte Carlo
Abstract
The stochastic Monte Carlo method is applied to solve partial differential equations with open boundary conditions, i.e., equations that have solutions in an infinite domain. First, we test the effectiveness of the Monte Carlo method by comparing results with the analytical solutions of known problems. Next, we applied the method to more complex physical problems that have no analytical solution. We found that in the case of the diffusion equation, the Monte Carlo method is applied directly on the infinite domain of the problem, while in the most popular numerical methods a bound solution domain is required.
Subject headings: Computational techniques and simulations Finite-difference methods Aplications of Monte Carlo methods
1. INTRODUCCIÓN
Fenomenos físicos en estado estacionario o en evolución temporal son expresados y modelados a través de EDP's elípticas y parabolicas respectivamente. Dependiendo de la complejidad de las condiciones de contorno y las condiciones iniciales, existen soluciones analíticas solo para casos simples y/o situaciones ideales. El grado de complejidad es aún mayor cuando las condiciones de contorno son abiertas, es decir cuando ciertos fenomenos físicos presentan el dominio de solución extendiéndose hasta el infinito, localizando las condiciones de contorno de manera parcial o total en el infinito.
Para fenomenos que tienen dominios de solución finito, existen varios metodos numéricos como por ejemplo: Diferencias Finitas, Elementos Finitos y Redes de Boltzmann solo por mencionar algunos. Mientras que, para fenomenos con dominios de solución infinito no se cuenta con una metodología numerica especıfica, pero en estos casos aun se pueden utilizar los metodos numéricos citados.
La metodología numerica trabaja solo sobre EDPs que tiene dominios de solucion discretizado y finito, debido a que generalmente se recurre al uso de matrices para representar el dominio de solucion, que obviamente debe ser finito. Por tanto, al aplicar algun método numérico para resolver una EDP que tiene un dominio de solucion infinito, es necesario acotar de alguna manera su dominio de solucion. En Sanjines (2006) se resuelve la ecuación de Laplace que tiene un contorno abierto mediante el metodo de Diferencias Finitas, previamente acotando el dominio de solucion infinito hasta una distancia razonable con respecto al centro del dominio.
Otra alternativa numerica un tanto diferente para resolver EDP's es el metodo de Monte Carlo, en ésta metodología se discretiza la EDP mediante Diferencias Finitas, pero no se requiere del uso de matrices para resolver la ecuacion en ningún momento. El proceso de discretizacion por Diferencias Finitas solo es necesario para obtener las Probabilidades de Transicion, que se utilizan en los Paseos Aleatorios que se simulan a traves de todo el dominio de solucion, tal como se puede ver en Suxo (2011). En síntesis, la solucion de una EDP por Monte Carlo se resume a: conteos, sumas y promedios, ademas no es necesario resolver globalmente el dominio de solucion como en los otros métodos citados, se puede resolver solo una parte de interés, e inclusive un sólo punto del dominio.
El metodo de Monte Carlo con las características intrínsecas que tiene, resulta ser un buen candidato para abordar fenomenos físicos que presentan un dominio de solucion infinito. En este trabajo se aplica esta metodología estocastica a dos fenómenos especıficos: el potencial y la difusión, procesos que son gobernados por las ecuaciones de Laplace y Difusion respectivamente. En primera instancia, se resuelven problemas bien conocidos que tienen soluciones analíticas con el fin de comparar resultados y observar la confiabilidad del metodo, y finalmente, el metodo se aplica a situaciones más complejas y reales que no cuentan con solucion analítica alguna.
2. SOLUCION NUMÉRICA DE UNA EDP Y CONDICIONES DE CONTORNO
2.1. Solución numérica de una EDP
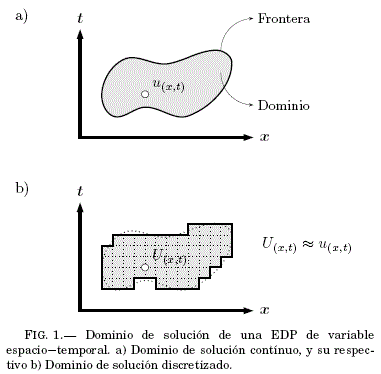
Si un determinado fenomeno físico ![]() , es expresado mediante una EDP, las condiciones de contorno y/o las condiciones iniciales de la ecuacion se encargan de particularizar y definir por completo la naturaleza del fenomeno. Las condiciones de contorno estan relacionadas a las variables espaciales (x, y, z), mientras que, las condiciones iniciales solo a la variable temporal (t), pero entre ambas condiciones forman la frontera1 del dominio de solucion de la EDP (vease Fig:1a, para el caso
, es expresado mediante una EDP, las condiciones de contorno y/o las condiciones iniciales de la ecuacion se encargan de particularizar y definir por completo la naturaleza del fenomeno. Las condiciones de contorno estan relacionadas a las variables espaciales (x, y, z), mientras que, las condiciones iniciales solo a la variable temporal (t), pero entre ambas condiciones forman la frontera1 del dominio de solucion de la EDP (vease Fig:1a, para el caso ![]() ), siendo la condicion inicial también un contorno.
), siendo la condicion inicial también un contorno.
Resolver una EDP mediante metodos numéricos, significa discretizar el dominio de solucion y su respectiva frontera (vease Fig:1b, para el caso ![]() ). Este proceso genera un sesgo de error en las soluciones halladas por el metodo numérico
). Este proceso genera un sesgo de error en las soluciones halladas por el metodo numérico ![]() respecto a la solucion exacta
respecto a la solucion exacta ![]() y Pero siempre es posible aproximar la solucion numérica a la exacta
y Pero siempre es posible aproximar la solucion numérica a la exacta![]() , reduciendo el error de la solucion hasta un grado de tolerancia segun la forma de discretización2 (Sheid (1968), Kreyszig (2006)).
, reduciendo el error de la solucion hasta un grado de tolerancia segun la forma de discretización2 (Sheid (1968), Kreyszig (2006)).
La solucion numérica ![]() es un conjunto discreto y finito que se expresa mediante una matriz:
es un conjunto discreto y finito que se expresa mediante una matriz:
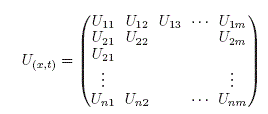
donde, la configuracion de los elementos de ésta matriz depende del tipo de EDP y su respectiva forma de discretizacion. Para hallar la solución ![]() se procede a traves de operaciones matriciales o resolver directamente el sistema de ecuaciones lineales (Sheid (1968), Press (2007)).
se procede a traves de operaciones matriciales o resolver directamente el sistema de ecuaciones lineales (Sheid (1968), Press (2007)).
2.2. Condición de Contorno Abierto (CCA)
Existen fenomenos físicos que tienen propiedades infinitas o fenomenos que interactúan con un entorno infinto, como por ejemplo: materia de dimensiones infinita o materia que se encuentra en un medio infinito, respectivamente. Las EDP's que representan estos fenómenos físicos, manifiestan el dominio de solucion de forma infinita ubicando la frontera en el infinito, es decir la frontera es abierta y el dominio es infinito.
Si un dominio de solucion infinito es sometido a una discretizacion, tanto el dominio como la frontera resultan ser tambien infinitos. Por tanto las condiciones de contorno discretizadas son abiertas, pero estan referidas especialmente a la dimensión espacial y no a la dimension temporal que es en sí un contorno abierto natural, que se extiende desde el presente (t = 0) hasta un tiempo futuro ( t> oo).
2.3. Solución Numérica de EDP's con CCA's
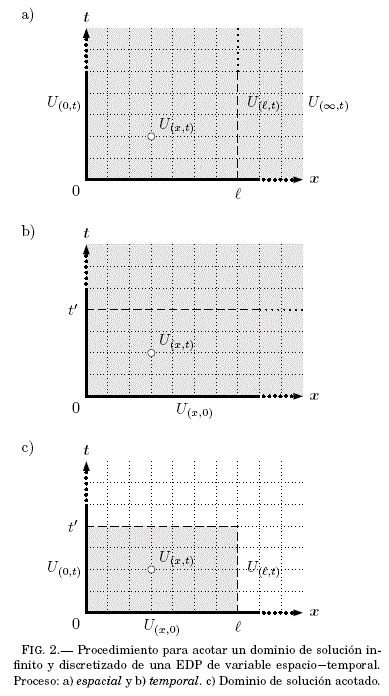
Para resolver numericamente EDP's con CCA's que previamente fue discretizado, es necesario acotar el dominio de solucion infinito: espacialmente y temporalmente. En el proceso de acotamiento del dominio infinito, es importante diferenciar entre el acotamiento debido a la parte: espacial y temporal.
En el acotamiento espacial el contorno ![]() es trasladado desde el infinito hasta una posicion finita
es trasladado desde el infinito hasta una posicion finita ![]() (vease Fig:2a), y ésta acción implica realizar una nueva aproximacion
(vease Fig:2a), y ésta acción implica realizar una nueva aproximacion ![]() en la solucion de la EDP, ademas de la aproximación debido a la discretizacion numérica. Mientras que, en el acotamiento temporal el contorno de la condicion inicial
en la solucion de la EDP, ademas de la aproximación debido a la discretizacion numérica. Mientras que, en el acotamiento temporal el contorno de la condicion inicial ![]() se ubican en t = 0, y el contorno ubicado en una posición
se ubican en t = 0, y el contorno ubicado en una posición ![]() no contiene datos del problema (vease Fig:2b), lo que indica que solo se realiza un corte (No es un proceso de traslado de contorno!) en el dominio de solucion sin generar aproximación alguna en la solucion de la EDP
no contiene datos del problema (vease Fig:2b), lo que indica que solo se realiza un corte (No es un proceso de traslado de contorno!) en el dominio de solucion sin generar aproximación alguna en la solucion de la EDP
La razon principal para acotar el dominio de solucion de una EDP con CCA, es transformar el dominio infinito a un dominio finito, con el fin de obtener un conjunto de solución U(x¿\ finito (vease Fig:2c). A continuacion, para hallar la solución de la EDP se puede proceder de la misma manera estandar, tal como se describio para la solución de una EDP con dominio de solucion finito.
3. CONDICIONES DE CONTORNO ABIERTAS Y EL METODO MONTE CARLO
3.1. Solución de EDP's por Monte Carlo
El metodo Monte Carlo es otra metodología numerica para resolver EDP's y es una conjunción de dos metodos: Diferencias Finitas y Paseos Aleatorios (Random Walk). La discretizacion de una EDP y su dominio de solucion a través de Diferencias Finitas, otorga las Probabilidades de Transición que requieren los Paseos Aleatorios que se simulan computacionalmente en el dominio de solucion discretizado. Para mas detalles ver Suxo (2011).
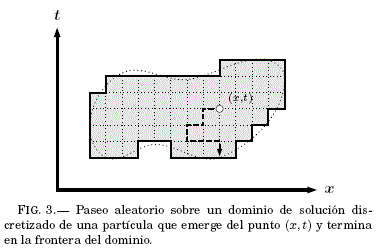
Segun el método Monte Carlo, el dominio de solucion es el ámbito donde se realizan los paseos aleatorios de un numero de partículas N que emergen de un determinado punto del dominio (x,t). Termina el paseo de una partıcula cuando llega a la frontera del dominio (vease Fig:3), y finalmente se procede a: contar, sumar y promediar los valores de la frontera donde llegaron las partículas para obtener la solución ![]() A medida que se incrementa el numero de partículas N se obtiene un mayor grado de exactitud en las soluciones
A medida que se incrementa el numero de partículas N se obtiene un mayor grado de exactitud en las soluciones ![]() (Sheid (1968)).
(Sheid (1968)).
Introducir Diferencias Finitas en Monte Carlo para resolver una EDP, no significa realizar un tratamiento matricial en dicho proceso. En el metodo de Monte Carlo, no es necesario el uso de matrices u otro recurso matematico para representar el dominio de solucion, siendo ésta la diferencia fundamental con las demas metodologías, como ser: Diferencias Finitas, Elementos Finitos, Volumenes Finitos, Redes de Boltzmann,..., etc (Sheid (1968), Press (2007), Mohamad (2011)). Otra particularidad crucial del metodo Monte Carlo, radica en que no es necesario resolver simultaneamente la totalidad del dominio de solucion (discreto), porque se procede a resolver el dominio punto a punto, es decir se puede resolver el dominio de solucion de manera: total, parcial o un punto individual.
3.2. Solución de EDP's con CCAs por Monte Carlo
Con las características expuestas que tiene el proceso de Monte Carlo mas las diferencias mencionadas con otras metodologías, el metodo Monte Carlo es el adecuado para resolver (numericamente) EDP's con CCA's por las siguientes razones:
a. Es posible abordar EDP's que poseen dominios de solucion infinitos a través de simulaciones com-putacionales, porque no se requieren herramientas matriciales. Caso contrario se necesitan matrices (arreglos) infinitas que no existen e imposibles en un computador.
b. No es necesario resolver de manera total el dominio de solucion de una EDP Es posible resolver solo una región de interés, evitando así el alto costo computacional, es decir: largos tiempos de simulación-ejecución.
c. Es posible programar el paseo aleatorio de partículas sobre un dominio de solucion infinito, debido a que durante la trayectoria no se realiza registro de datos. Solo se verifica el punto de la frontera al cual llega una partícula para proceder a sumar su valor.
Para resolver satisfactoriamente EDP's con CCA's mediante el metodo de Monte Carlo, es imperativo garantizar que: los paseos aleatorios arriben a buen puerto, es decir las partículas que emergen de un punto del dominio deben terminar necesariamente en la frontera (en una condicion de contorno ó condicion inicial). De lo contrario, el paseo aleatorio de una partícula no terminarıa jamás.
La forma de proceder para garantizar que un paseo aleatorio arribe a buen puerto, depende del fenomeno físico (tipo de EDP: elıptica, parabólica o hiperbolica). A continuación, se ilustra en detalle la manera de garantizar el requisito mencionado, resolviendo las ecuaciones de: Laplace y Difusion, que modelan fenomenos estacionarios y de evolución temporal respectivamente.
3.3. Ecuación de Laplace
La ecuacion de Laplace pertenece al tipo EDP elíptica, por tanto representa a fenomenos estacionarios y tiene como frontera del dominio solo condiciones de contorno.
Problema: Capacitor esferico de radio R conformado por dos hemisferios que se encuentran a un mismo potencial electrico Vo pero de signo contrario (vease Fig:4). Hallar el potencial fuera del capacitor.
Solución: Debido a la geometría del capacitor, el potencial electrico se expresa en coordenadas esféricas ![]() y por su simetría azimutal
y por su simetría azimutal ![]() finalmente es expresado como:
finalmente es expresado como: ![]() y La EDP que modela el potencial electrico y sus respectivas condiciones de contorno se muestran a continuacion:
y La EDP que modela el potencial electrico y sus respectivas condiciones de contorno se muestran a continuacion:
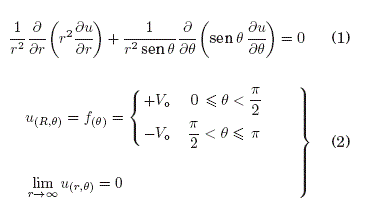
donde, la ecuacion representa a una EDP con CCA.
Para resolver el problema mediante el metodo de Monte Carlo, en primer lugar se debe discretizar la EDP (Ec:1) a traves del método de Diferencias Finitas utilizando las siguientes aproximaciones:
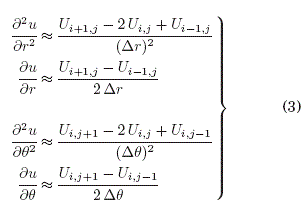
donde, el valor discreto: ![]() y de manera semejante se relacionan los valores vecinos. Las derivadas angulares se desarrollan en diferencias finitas centrales para obtener una simetría polar (necesaria en el contorno periodico, ver Fig:5), mientras que, en las derivadas radiales es indiferente cualquier desarrollo.
y de manera semejante se relacionan los valores vecinos. Las derivadas angulares se desarrollan en diferencias finitas centrales para obtener una simetría polar (necesaria en el contorno periodico, ver Fig:5), mientras que, en las derivadas radiales es indiferente cualquier desarrollo.
Reemplazando las Ecs:3 en la Ec:1 y despejando el punto central ![]() 0se obtiene la ecuacion que otorga las Probabilidades de Transicion (Ec:4) hacia los cuatro puntos vecinos:
0se obtiene la ecuacion que otorga las Probabilidades de Transicion (Ec:4) hacia los cuatro puntos vecinos:
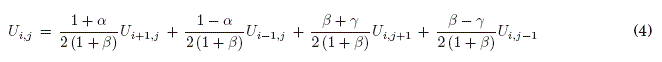
donde, las variables a, B y 7 tienen valores igual a:
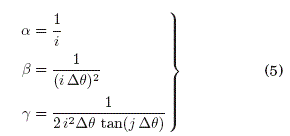
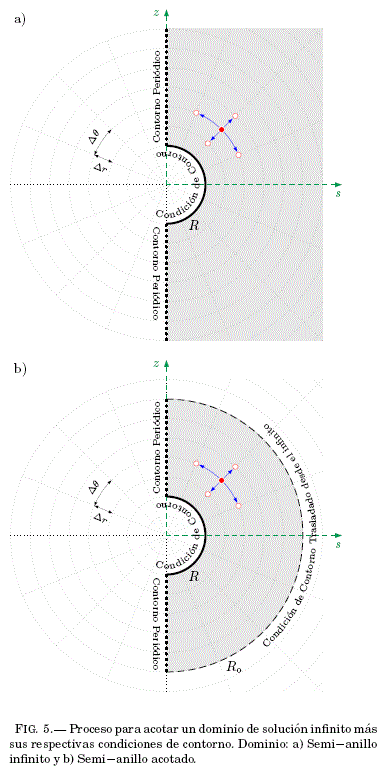
Las Probabilidades de Transicion (Ec:4) son la herramienta del metodo de Monte Carlo para resolver la ecuacion de Laplace (Ec:1), simulando paseos aleatorios sobre el dominio de solucion: el semianillo infinito adherido al plano sz (vease Fig:5a). La frontera del dominio esta conformada por: a) un contorno periodico a lo largo del eje z, mas dos contornos semi-circulares de b) radio R y c) radio infinito3.
El paseo aleatorio acaba su recorrido solo cuando arriba al contorno semi-circular de radio R, si por el contrario en su paso se encuentra con un contorno periodico, el paseo sufre una reflexión especular debido a la simetría polar continuando su recorrido4.
Pero, debido a las cuatro direcciones posibles de transicion, el paseo puede realizar un recorrido hacia el contorno de radio infinito sin poder alcanzarlo, lo que significaría un recorrido sin fin.
Para garantizar que: un paseo aleatorio arribe a buen puerto, se sigue la tecnica sugerida en Sanjinés (2006). Trasladar el contorno de radio infinito hasta un radio razonable pero finito Ro (vease Fig:5b), lo que significa realizar una aproximacion en los valores del contorno:![]() . La presicion esta en función del valor asignado al radio Ro. Resultado: El potencial electrico exterior al capacitor encontrado es una superficie
. La presicion esta en función del valor asignado al radio Ro. Resultado: El potencial electrico exterior al capacitor encontrado es una superficie ![]() , pero se representa a traves de líneas equipotenciales (curvas de nivel de la superficie), con el fin de comparar con la solucion analítica (Simmons (2002), Kreyszig (2006)) siguiente:
, pero se representa a traves de líneas equipotenciales (curvas de nivel de la superficie), con el fin de comparar con la solucion analítica (Simmons (2002), Kreyszig (2006)) siguiente:
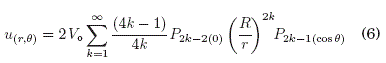
donde, se utilizan los valores: R = 4cmyVo = 100 V.
El dominio es acotado hasta un radio Ro = 100 cm, formando un dominio para los paseos aleatorios igual a: ![]() , donde para un determinado punto del dominio
, donde para un determinado punto del dominio ![]() se simulan: N = 5000 y 50000 partículas. En el proceso de discretizacion del dominio de solución, en la parte radial:
se simulan: N = 5000 y 50000 partículas. En el proceso de discretizacion del dominio de solución, en la parte radial: ![]() y en la parte angular:
y en la parte angular:![]() .
.
Debe notarse que, existe indeterminacion en la variable ![]() de las Ecs:5 cuando
de las Ecs:5 cuando ![]() debido al termino trigonométrico
debido al termino trigonométrico ![]() . Sin embargo, ambas posiciones corresponden al contorno periodico donde ocurre la reflexión especular del paseo aleatorio, proceso en el cual se simplifica la variable
. Sin embargo, ambas posiciones corresponden al contorno periodico donde ocurre la reflexión especular del paseo aleatorio, proceso en el cual se simplifica la variable ![]() al sumar los coeficientes angulares (probabilidades de transicion: horario y antihorario) de la Ec:4.
al sumar los coeficientes angulares (probabilidades de transicion: horario y antihorario) de la Ec:4.
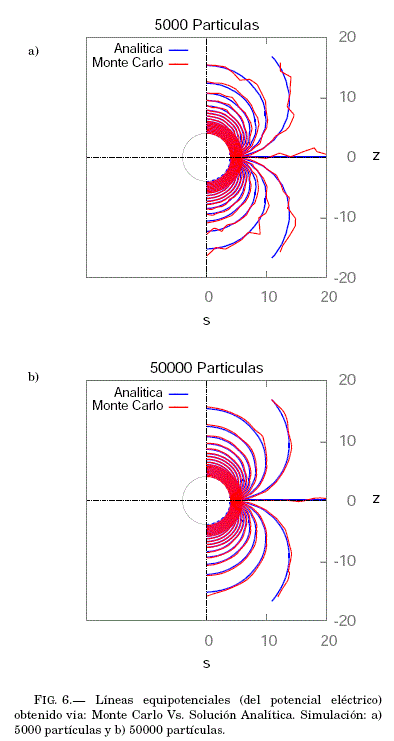
Se obtuvieron resultados ![]() para una parte central del dominio:
para una parte central del dominio: ![]() , que se exponen en la Fig:6 en comparacion con la solución analítica (Ec:6). En la figura se observa la efectividad del metodo Monte Carlo, así como también su presicion a medida que se incrementa el número de partículas.
, que se exponen en la Fig:6 en comparacion con la solución analítica (Ec:6). En la figura se observa la efectividad del metodo Monte Carlo, así como también su presicion a medida que se incrementa el número de partículas.
3.4. Ecuación de Difusión
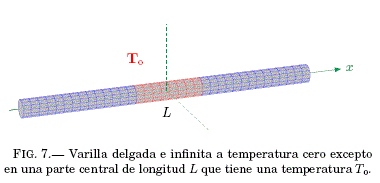
La ecuacion de Difusión perteneciente al tipo de EDP parabolica representa matemáticamente a fenomenos físicos de evolucion temporal, y la frontera del dominio esta conformada por: condiciones de contorno y una condicion inicial. Problema: Una varilla delgada de longitud infinita y aislada lateralmente se encuentra a una temperatura igual a cero, excepto en una parte de longitud L ubicada en el centro y tiene una temperatura To (vease Fig:7). Hallar la difusión de la temperatura
en la varilla para cinco instantes de tiempo (con un coeficiente de difusion del material6: A). Solución: La temperatura en la varilla es expresado en coordenadas cartesianas: ![]() . La EDP que modela la temperatura mas sus respectivas condiciones de contorno y condicion inicial, es la siguiente:
. La EDP que modela la temperatura mas sus respectivas condiciones de contorno y condicion inicial, es la siguiente:
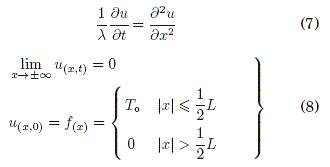
donde, la ecuacion representa a una EDP con CCA.
Para resolver el problema primero discretizamos la EDP (Ec:7) mediante Diferencias Finitas utilizando las siguientes aproximaciones:
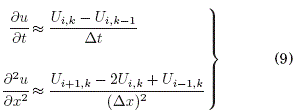
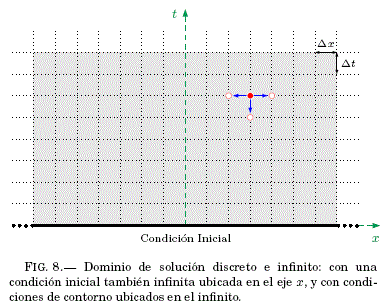
donde, el valor discreto: ![]() y de manera similar se relacionan los valores vecinos. Es necesario utilizar diferencias finitas hacia atrás en la derivada temporal, para obtener el sentido de la direccion temporal (eje vertical) hacia el pasado (abajo), ver Fig:8.
y de manera similar se relacionan los valores vecinos. Es necesario utilizar diferencias finitas hacia atrás en la derivada temporal, para obtener el sentido de la direccion temporal (eje vertical) hacia el pasado (abajo), ver Fig:8.
Reemplazando las Ecs:9 en la Ec:7 y depejando el punto central ![]() se obtiene la ecuacion que otorga las Probabilidades de Transicion (Ec:10) hacia los tres puntos vecinos:
se obtiene la ecuacion que otorga las Probabilidades de Transicion (Ec:10) hacia los tres puntos vecinos:
![]()
donde, el valor a es el criterio de convergencia7 igual:
![]()
Las Probabilidades de Transicion (Ec:10) usados en Monte Carlo resuelven la ecuacion de Difusión (Ec:7), simulando paseos aleatorios sobre el dominio de solucion: el semi-plano infinito xt (vease Fig:8). La frontera del dominio esta conformada por: a) Dos condiciones de contorno (lıneas verticales infinitas) ubicados en el infinito positivo y negativo del eje x, mas b) una condición inicial (línea horizontal infinita) extendida a lo largo del eje x.
Los paseos aleatorios tienen tres direcciones de transicion: dos horizontales (izquierda-derecha) y una vertical hacia abajo (vease Fig:8). Por tanto, los paseos aleatorios en su recorrido van bajando gradualmente para finalmente terminar en la condicion inicial, y no en las condiciones de contorno ubicadas en el infinito8. En conclusión, que un paseo aleatorio arribe a buen puerto: ¡ esta garantizada! sin la necesidad de acotar el dominio de solucion infinito. Resultado: La evolucion temporal de la temperatura en la varilla infinita es una superficie ![]() , pero se representa mediante la función
, pero se representa mediante la función ![]() por cada t con el fin de comparar con la solucion analítica (Simmons (2002), Kreyszig (2006)) siguiente:
por cada t con el fin de comparar con la solucion analítica (Simmons (2002), Kreyszig (2006)) siguiente:
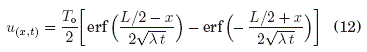
donde, los datos: ![]() .
.
Los paseos aleatorios se realizan sobre un dominio semi-infinito (sin acotar) igual a:![]() y
y ![]() , donde para un determinado punto del dominio
, donde para un determinado punto del dominio ![]() se simulan: N = 1000 y 10000 partículas. En el proceso de discretizacion del dominio de solucion, en la parte espacial:
se simulan: N = 1000 y 10000 partículas. En el proceso de discretizacion del dominio de solucion, en la parte espacial:![]() con i = -50, -49,..., 0,..., 49, 50 y en la parte temporal:
con i = -50, -49,..., 0,..., 49, 50 y en la parte temporal: ![]() con k = 0,1,2 ..., 1190.
con k = 0,1,2 ..., 1190.
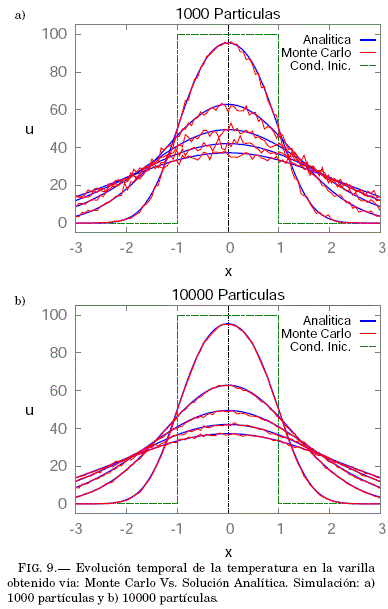
Se obtuvieron resultados ![]() para una parte central de la varilla:
para una parte central de la varilla:![]() para cinco instantes de tiempo:
para cinco instantes de tiempo: ![]() , que se exponen en la Fig:9 en comparacion con la solución analítica (Ec:12). La figura muestra la efectividad del metodo Monte Carlo, y tambien su presición a medida que se incrementa el numero de partículas simuladas com-putacionalmente.
, que se exponen en la Fig:9 en comparacion con la solución analítica (Ec:12). La figura muestra la efectividad del metodo Monte Carlo, y tambien su presición a medida que se incrementa el numero de partículas simuladas com-putacionalmente.
4. APLICACIONES
La efectividad del metodo Monte Carlo para resolver EDP's con CCA's ha sido comprobada, ahora se aplica la metodología descrita para resolver problemas que no cuentan solucion analítica.
4.1. Potencial eléctrico entre una Esfera hueca y una Varilla delgada
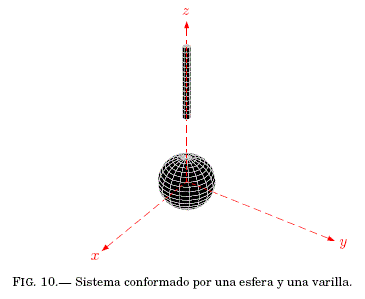
El estudio realizado al capacitor esferico en la Sec:3.3 es la base de este problema. Ahora, el capacitor es la esfera hueca y una varilla delgada se incluye radialmente al sistema (vease Fig:10). El problema consiste en encontrar el potencial electrico de interaccion entre ambos objetos.
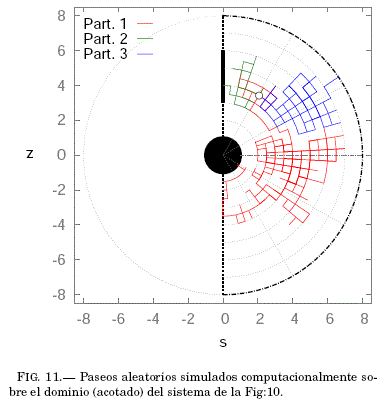
En el dominio de solucion (previamente acotado) donde se producen los paseos aleatorios se incluye la varilla9, tal como se ve en la Fig:11. La figura muestra tres paseos aleatorios (de partículas) simulados computacionalmente: 1) la roja arriba a la esfera previamente pasando por un contorno periodico, 2) la verde arriba a la varilla y 3) la azul arriba al contorno trasladado desde el infinito.
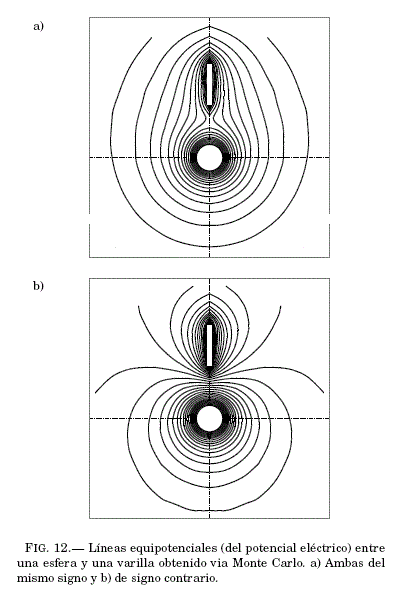
En el estudio, los contornos Esfera-Varilla se encuentran a un mismo potencial electrico ±V0 en dos casos diferentes: a) ambas del mismo sigo y b) de signo contrario. Los resultados obtenidos en ambas situaciones se exponen en la Fig:12, los cuales se representan por lineas equipotenciales.
4.2. Difusión de la Concentración de un sector circular en el Plano
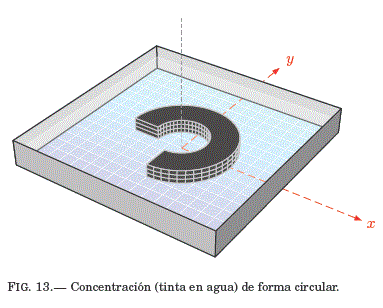
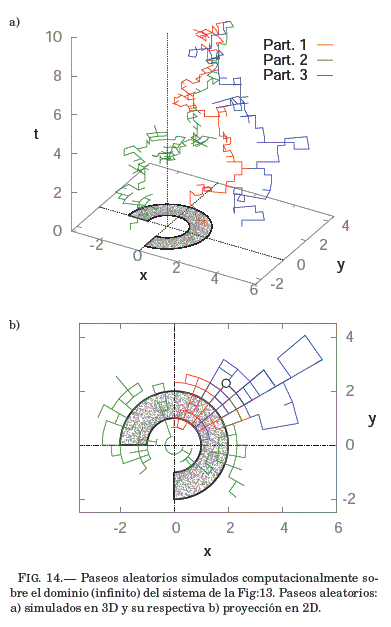
Se estudia la ecuacion de Difusión en coordenadas polares, y los detalles para transformar la EDP en una ecuacion de Probabilidades de Transición se expone en el Ape:A. El problema consiste en encontrar la evolucion temporal de una determinada configuracion de concentración: ![]() , que en un inicio tiene la forma de un sector circular (vease Fig:13).
, que en un inicio tiene la forma de un sector circular (vease Fig:13).
El dominio de solucion es un volumen cilindrico infinito (que descansa sobre el plano xy), por tanto su frontera esta conformada por: a) el área lateral cilindrica (de radio y altura infinita) ubicada en el infinito como condición de contorno, mas b) el circulo (de radio infinito) ubicado sobre el plano xy como condición inicial (vease Fig:14).
Un paso aleatorio tiene cinco posibles direcciones de transicion: cuatro espaciales-polares (horizontales paralelos al plano xy) y una temporal (vertical hacia abajo). En la Fig:14a, se muestran tres paseos aleatorios sobre el dominio infinito que fueron simulados computacionalmente: todas arriban a la condicion inicial, donde sólo una de ellas (partícula roja) llega al sector circular, mientras las restantes acaban fuera del sector (partículas, verde y azul).
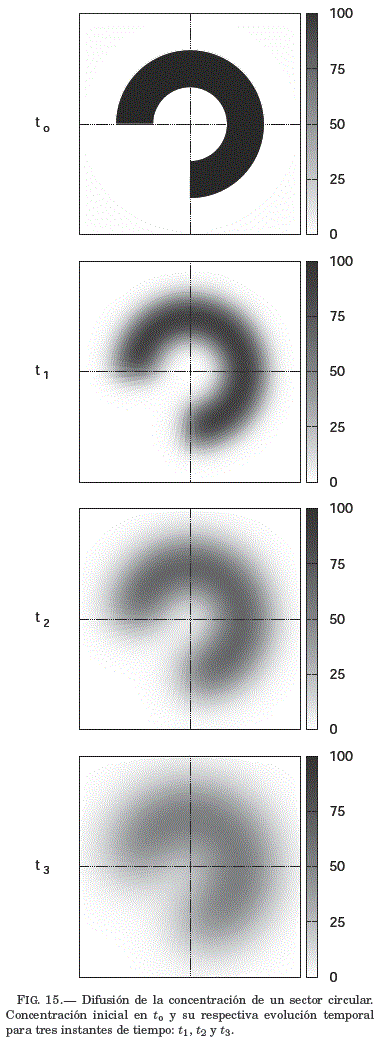
En el estudio, el sector circular tiene una concentración Co que puede representar a una mancha de tinta presente en agua, donde el recipiente es extremadamente amplio pero de muy poca profundidad. Se obtuvieron resultados sobre el proceso de difusion de la concentración para tres instantes de tiempo, que se exponen en la Fig:15.
5. CONCLUSIONES
Es posible resolver las ecuaciones de: Laplace y Difusion que tienen condiciones de contorno abiertas mediante el metodo Monte Cario, l) En la ecuacion de Laplace es necesario acotar el dominio de solucion infinto previamente para su posterior solucion por Monte Carlo, mientras que, 2) en la ecuacion de Difusion el método Monte Carlo trabaja directamente sobre el dominio de solucion infinito, sin la necesidad de acotar el dominio.
Justamente, en los resultados del caso dos radica la importancia de este trabajo, porque las metodologıas numericas popularmente usadas no pueden trabajar sobre dominios infinitos directamente, deben acotar siempre el dominio de cualquier EDP incluido la ecuacion de Difusión.
6. PERSPECTIVAS
La posibilidad de trabajar con la ecuacion de Difusion sin someterlo a procesos de acotamiento, nos motiva a explorar procesos de difusion más complejos, como ser: a) difusion en tres dimensiones ó b) difusion en presencia de obstáculos físicos c) para su posterior aplicacion a difusión en conductos porosos abiertos e infinitos.
Tambien existe la posibilidad de estudiar fenomenos de transporte más complejos como ser: procesos difusivos y advectivos simultaneamente, en el cual la ecuación que gobierna estos procesos es la ecuacion de difusión-advección:
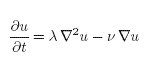
donde, A es el coefifiente de difusion y v la velocidad del sistema. Esta ecuacion es la base de los modelos que describen la propagacion de contaminantes en el aire, derramamientos de petroleo en el mar, etc, procesos que son de relevada importancia en la actualidad debido a los problemas ambientales que atraviesa el planeta.
APENDICE
A. METODO DE MONTE CARLO PARA: ECUACIÓN DE DIFUSION EN COORDENADS POLARES
La ecuacion de Difusión en coordenadas polares que modela un fenomeno físico ![]() , es expresado de la siguiente manera:
, es expresado de la siguiente manera:
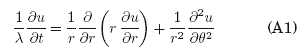
El metodo Monte Carlo requiere discretizar la EDP para obtener un dominio de solucion discreto, para el ambito de los paseos aleatorios, por tanto se desarrolla la EDP en Diferencias Finitas a traves de las siguientes aproximaciones:
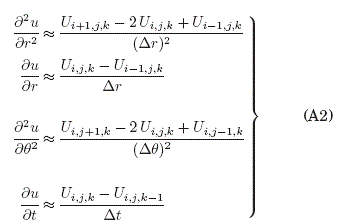
donde, el valor ![]() y de manera semejante se relacionan los demas valores vecinos:
y de manera semejante se relacionan los demas valores vecinos: ![]() Es necesario hacer uso de diferencias finitas hacia atrás en la parte temporal y en la primera derivada de la parte radial. En el primer caso, para obtener el sentido de la direccion temporal hacia el pasado para que los paseos aleatorios siempre terminen en la condicion inicial del problema (ver Fig:14a). En el segundo caso, el objetivo es impedir que los paseos aleatorios se encuentren con el origen de coordenadas (punto indeterminado), es decir que la probabilidad de transicion hacia el origen sea igual a cero cuando se encuentren a un paso del origen (ver Fig:14byEc:A3).
Es necesario hacer uso de diferencias finitas hacia atrás en la parte temporal y en la primera derivada de la parte radial. En el primer caso, para obtener el sentido de la direccion temporal hacia el pasado para que los paseos aleatorios siempre terminen en la condicion inicial del problema (ver Fig:14a). En el segundo caso, el objetivo es impedir que los paseos aleatorios se encuentren con el origen de coordenadas (punto indeterminado), es decir que la probabilidad de transicion hacia el origen sea igual a cero cuando se encuentren a un paso del origen (ver Fig:14byEc:A3).
Reemplazando las aproximaciones (A2) en la EDP (A1) y depejando el termino central ![]() se obtiene la ecuacion que otorga las Probabilidades de Transicion (A3) hacia los cinco puntos vecinos.
se obtiene la ecuacion que otorga las Probabilidades de Transicion (A3) hacia los cinco puntos vecinos.
Las direcciones de transicion son de dos tipos: las espaciales y la temporal. En las espaciales dos son radiales (hacia: adentro y fuera del origen) y las otras dos son angulares (direccion: horario y antihorario), mientras que, la temporal es hacia atras ó hacia el pasado (vertical hacia abajo).
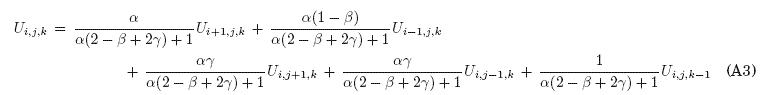
donde la variable a y B y ![]() tienen los valores:
tienen los valores:
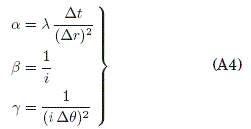
y las variables ![]() indican el criterio de convergencia impuestos por la utilización del método de Diferencias Finita:
indican el criterio de convergencia impuestos por la utilización del método de Diferencias Finita:
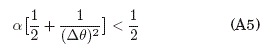
NOTAS
1 En el caso mas general la frontera encierra a un hiper-espacio xyzt y en un caso sencillo—didactico encierra a un plano xt.
2 Por ejemplo: en EDP's elípticas se utiliza el metodo de discretizacion de Liebmann, mientras que, en las parabólicas se hace uso del metodo de Crank—Nicolson.
3 El radio infinito no es posible representar graficamente. Por totra parte, el eje s se encuentra confinado al plano xy y puede asignarse cualquier direccion debido a la simetría azimutal.
4 Sumando los terminos angulares ![]() se genera el termino de reflexión especular
se genera el termino de reflexión especular ![]() . Por tanto, cuando la partícula se encuentra en el eje z se utiliza la ecuacion:
. Por tanto, cuando la partícula se encuentra en el eje z se utiliza la ecuacion:
![]()
5 Existe la posibilidad de indeterminacion para 8 = π/2, pero es evitado dividiendo el rango angular π por un numero impar.
6 Definido por: ![]() donde, re es la conductividad termica, a el calor específico y p la densidad del material.
donde, re es la conductividad termica, a el calor específico y p la densidad del material.
7 El metodo Diferencias Finitas impone que se cumpla:![]() .
.
8 Respetando el criterio de convergencia, la probabilidad de un paso hacia abajo es: ![]() . Es decir, es mas probable el movimiento vertical (hacia la condicion inicial) a los horizontales.
. Es decir, es mas probable el movimiento vertical (hacia la condicion inicial) a los horizontales.
9 La inclusion de la varilla en el dominio, no rompe la simetría azimutal del problema debido a su posicion estratégica.
REFERENCIAS
Kreyszig E. (2006), Advanced Engineering Mathematics (John Wiley & Sons) [ Links ]
Mohamad A. (2011), Lattice Boltzmann Method Fundamentals and Engineering Applications with Computer Codes (Springer) [ Links ]
Press W. (2007), Numerical Recipes 3rd Edition (Oxford University Press) [ Links ]
Sanjines D. (2006), Revista Boliviana de Física 12, 17 [ Links ]
Sheid R (1968), Numerical Analysis (McGraw-Hill) [ Links ]
Simmons G. (2002), Differential Equations with Applications and Historical Notes (McGraw-Hill) [ Links ]
Suxo R (2011), Revista Boliviana de Física 19, 24 [ Links ]