ARTÍCULOS

 

Espacios de parámetros para el estudio de la turbulencia mediada por defectos y otros fenómenos no
lineales en sistemas espacialmente distribuidos

 

Parameter spaces for studying defect-mediated turbulence and other nonlinear phenomena in spatially distributed systems

 

 

J. W. Sirpa Poma^† & G. M. RamIrez Ávila^‡
Instituto de Investigaciones Físicas, Carrera de Fısica
Universidad Mayor de San Andres
c. 27 Cota-Cota, Campus Universitario, Casilla de Correos 8635
La Paz - Bolivia
(Recibido 15 de noviembre de 2015; aceptado 17 de diciembre de 2015)

 

 

---

Resumen

Se utiliza la ecuacion compleja de Landau-Ginzburg (ECLG) como base para el estudio de sistemas espacialmente distribuidos. Se considera diferentes comportamientos de un fluido tales como la laminaridad, la aparicion de fuentes y sumideros, el régimen intermitente, la turbulencia de fase y la turbulencia mediada por defectos, siendo esta la que en principio concito nuestra atención. El análisis numérico de la ECLG nos permitió caracterizar espacio-temporalmente cada uno de estos comportamientos. Por medio de la construccion del espacio de parametros con base en la amplitud promedio, se identifican cada uno de estos regímenes.

Codigo(s) PACS: 47.27.Cn, 02.70.-c, 05.45.-a

Descriptores: Transicion a la turbulencia — Técnicas computacionales; simulaciones — Dinamica no lineal y caos.

---

Abstract

The complex Landau-Ginzburg equation (CLGE) has been used as the basis of the study of spatially distributed systems. We considered a variety of behaviors on a fluid, such as lami-narity, the apparition of sources and sinks, the intermittent regime, and the defect-mediated turbulence; being the last one that focused our attention. Numerical analysis of the CLGE allowed us the spatio-temporal characterization of each of these behaviors. By means of the parameters space, based on the mean amplitude, the phase diagram distinguishes clearly the occurrence of the above mentioned regimes.

Subject headings: Transition to turbulence — Computational techniques; simulations — Nonlinear dynamics and chaos.

---

 

 

1. INTRODUCCION

La comprension del orden espacio-temporal en sistemas abiertos alejados del equilibrio termodinamico y sus simetrías es un tema importante de investigacion dentro de las estructuras de la materia continua. Es tambien conocido que las transiciones laminar/turbulento en fluidos son una consecuencia del orden espacio-temporal como lo senalan Walgraed & Ghoniem (1990).

Uno de los trabajos paradigmaticos en el estudio de organizacion espacio-temporal es el propuesto por Turing (1952) que analiza la morfogenesis a partir de una inestabilidad que hace alusion a la ruptura de simetría, donde la longitud caracterıstica es intrínseca al sistema (dependiendo solamente de los parametros y no así de la geometría ni de las condiciones de frontera).

La conveccion térmica es el origen de importantes y sorprendentes fenomenos naturales; entre ellos, la circulacion de la atmósfera y océanos, el movimiento de placas continentales, etc. Este problema fue abordado mediante un sencillo experimento a escala en 1900 por Benard, y que desembocó en una gran cantidad de propiedades interesantes; siendo la principal, la aparicion de multiestabilidad cuando se supera el valor crítico de la temperatura.

Así, no es sorprendente encontrar inestabilidades y bifurcaciones en una gran variedad de sistemas conocidos, tales como el flujo de vortices de Taylor, dinamica de solidificación, física de láseres y muchos otros que guardan similaridad con las observadas en el problema de Benard y en sistemas de reacción-difusion tal como lo señala Nicolis (1995).

En la Sec. 2 se presenta el modelo que se utiliza para el estudio de sistemas espacialmente distribuidos que luego de un analisis de estabilidad lineal se llega a la forma normal en la vecindad de una inestabilidad, lo que se constituye en la ECLG, la cual es la base para los analisis ulteriores. En la Sec. 3 se dan los detalles del metodo utilizado para la resolución de la ECLG. En la Sec. 4 se muestran los resultados mas importantes usando espacios de parámetros y finalmente se mencionan las conclusiones y perspectivas en la Sec. 5.

 

2. MODELO

Para el estudio de cada uno de los sistemas mencionados, se tiene una variedad de modelos matematicos dependiendo del tipo de inestabilidades que se vayan a presentar. Entre los mas habituales estan los expuestos por Cross & Hohenberg (1993), de los cuales, se pueden mencionar: la ecuacion de Swift-Hohenberg (SH) y sus variantes para inestabilidades del tipo estacionario-periodico; la ecuación de Kuramoto-Sivashinky (KS) que representa un modelo microscopico; las ecuaciones de reacción-difusion para inestabilidades de tipo oscilatorio-uniforme para la descripcion de reacciones químicas; y por ultimo el modelo de Landau-Ginzburg, el cual es adecuado para sistemas espacialmente distribuidos.

La descripcion de sistemas compuestos por muchas partículas esta dada a través de muchas variables de estado que dependen continuamente de las coordenadas espaciales y que obedecen las leyes de la física clasica. De manera general, las leyes de evolución de estas variables de estado se las expresa en terminos de ecuaciones diferenciales en derivadas parciales de la forma:

 

Sistemas representados con la anterior ecuacion son denominados sistemas espacialmente distribuidos y en principio a causa de inhomogeneidades espaciales, llegan a tener una infinidad de variables que pueden estar acopladas por fenomenos de transporte. Por otra parte, la presencia de derivadas espaciales posibilita la aparicion de inestabilidades espontaneas de ruptura de simetría. En otros terminos, esta aparición indica la existencia de una dependencia espacial de las perturbaciones.

Ademas, los sistemas con gran extensión espacial, a diferencia de los sistemas espacialmente pequenos, llegan a presentar nuevas caracterısticas por el hecho de poseer un numero mayor de grados de libertad.

Considerando un numero finito de variables de manera que las restricciones actuando sobre el sistema no dependan del tiempo (sistemas autonomos), se tendra que las leyes de evolución pueden ser escritas de manera mas compacta:

donde es el parametro de control, el cual refleja la estructura interna del sistema o la manera en que se comunica con el mundo externo. Los sistemas reales presentan un gran conjunto de parametros, entre los mas conocidos podemos mencionar los coeficientes de viscosidad, el coeficiente de difusion, etc.

Por otra parte, las soluciones estan bien definidas en el espacio de fases , excepto en algunos puntos , puntos que son determinados a partir de un conjunto de ecuaciones algebraicas:

 

Dichos puntos reciben la denominacion de puntos singulares. En sistemas autonomos estos puntos permanecen fijos en el espacio de fases permanentemente, definiendo un conjunto invariante y describiendo soluciones estacionarias.

En los sistemas reales se observa que no permanecen en un solo estado a lo largo del tiempo; se tiene así, un conjunto de variables que interactuan de manera compleja intercambiando masa, momentum y energía de manera impredecible. Como resultado se tiene una desviacion constante alrededor de las soluciones estables, nos referimos a estas como una perturbacion.

 

Dependiendo de la respuesta del sistema ante una perturbacion se puede inferir si el sistema es estable, inestable o asintoticamente estable. Realizando una expansion de Taylor en términos de alrededor de , la ecuacion adopta la siguiente forma:

donde se tiene una contribucion de una parte lineal y otra no lineal, esta ultima en correspondencia con terminos de orden superior en el desarrollo de Taylor. Para la descripcion generalizada, se incluye la derivada espacial conjuntamente con un analisis de bifurcacion de Hopf en sistemas espacialmente uniformes, con lo que se llega a obtener la forma normal de la dinamica en sistemas espacialmente distribuidos, en la vecindad de una inestabilidad . En la literatura se la denomina como la ecuacion compleja de Landau-Ginzburg (ECLG):

 

donde los parametros son parametros asociados al punto de bifurcacion (transiciones en la estabilidad), a la dispersion lineal y no lineal (o conservacion de la no linealidad), respectivamente.

Realizando un analisis de estabilidad lineal de la anterior ecuacion se llega a obtener soluciones estacionarias de la forma:

 

Considerando soluciones generales o perturbadas:

 

y reemplazando en la ECLG se llega a obtener la ecuacion característica descrita por Nicolis (1995), producto de esta se tiene el criterio de Benjamin-Feir-Newell, demostrando que la unica inestabilidad puede surgir cuando se cumple la desigualdad Lo contrario garantiza soluciones en el regimen laminar; dicha inestabilidad se presenta en forma de turbulencia espacio-temporal caracterizada por la aparicion espontánea de defectos como muestra Conway (2008).

Otros comportamientos encontrados son la turbulencia de fase caracterizada por tener amplitudes saturadas, el regimen de turbulencia mediada por defectos caracterizada por un caracter caótico que puede incluir amplitudes de valor cero; por ultimo se tiene un regimen intermitente caracterizado por la coexistencia entre la turbulencia mediada por defectos y ondas planas estables (laminaridad), lo que tıpicamente se presenta como regiones laminares separadas por estructuras localizadas con una gran depresion de la amplitud. Además, estas estructuras localizadas pueden llegar a formar fuentes y sumideros bajo ciertos valores de los parametros como lo mencionan Rabinovich et al. (2000). En este trabajo se caracterizan los diferentes regímenes de un fluido.

 

3. METODOS PARA LA RESOLUCIÓN DE LA ECLG

En este trabajo, se resuelve la ECLG en una dimension utilizando el método pseudoespectral para la discretizacion espacial y el método de diferenciacion de tiempo exponencial (ETD por su sigla en ingles) para la discretización temporal, método que nos proporciona una alta resolucion de los resultados en comparacion al método de diferencias finitas.

3.1.  Discretización Espacial

El metodo utilizado para resolver la parte espacial de la ECLG, es el denominado pseudoespectral de Fourier, esto con el fin de no perder resolucion en las soluciones numericas ya que el orden del error esta en función del modo de oscilación y del orden maximo de la derivada espacial . Este metodo consiste en escribir las soluciones como una combinacion lineal de funciones base, en este caso funciones base de Fourier ; ademas, nos permite trabajar facilmente con la derivada espacial.

Así, se analiza la ECLG en el espacio de Fourier, esto es, aplicando la transformada de Fourier (ver (9)) y calculando los coeficientes de Fourier a partir de la transformada discreta de Fourier (TDF) como indica Geldhof (2013).

 

Se trabajo en el intervalo de [-100,100] con condiciones de contorno periodicas, con una grilla de 0.4.

3.2.  Discretización Temporal

Nuestro interes es ver la evolución de la ecuación no lineal (9). Ası, reescribiendo la ecuación vemos que esta tiene la contribucion de una parte lineal y otra no lineal de la forma:

 

Ecuaciones con esta forma pueden ser resueltas por el metodo ETD, consistente en multiplicar la ecuacion por el factor de integración , donde representa la parte lineal de la ecuacion (10), e integrando en el intervalo

 

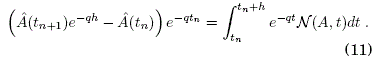
Esta relacion es exacta, y la esencia de este método es derivar aproximaciones de la integral (11). Este metodo cuenta con muchas variantes ya sea aproximaciones de primer orden (ETD1) o de segundo orden (ETD2) de la integral por diferencias, o la combinacion con otros métodos (p.ej. Runge-Kutta). Sin embargo, teniendo en cuenta que los procesos son de variacion lenta se opta por una aproximación de primer orden en la integral como lo senalan Cox & Matthew (2002) obteniendo así:

 

En el presente trabajo se escogio como paso de tiempo , como compromiso de no extender demasiado el tiempo de calculo y de no perder resolucion en las soluciones.

 

4. RESULTADOS

Con base en las soluciones numericas de (12), aplicando la transformada inversa de Fourier, y variando los valores de se puede observar distintos patrones espacio-temporales, desde laminaridad hasta turbulencia mediada por defectos en la region de inestabilidad.

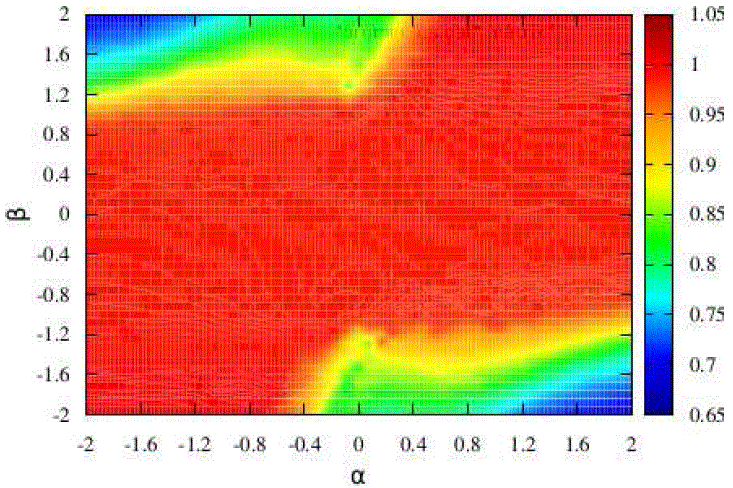
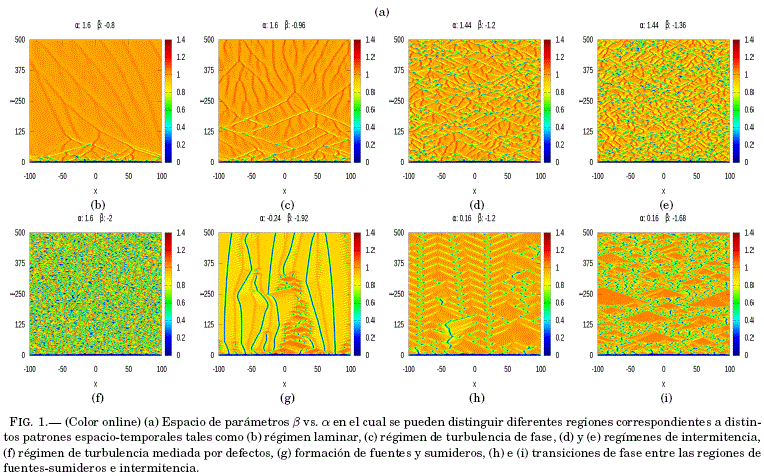
En concreto, se varió en un intervalo de [-2, 2] con pasos de 0.08. Se obtuvieron multiples patrones espacio-temporales, incluyendo la region de turbulencia mediada por defectos. Con el fin de caracterizar la region en consideración fue imperativo el tener un criterio con el cual se puedan distinguir los diferentes regımenes del sistema. Es así que se opto por calcular el promedio de las amplitudes de cada uno de los patrones espacio-temporales resultantes, obteniendo ası los valores para construir el espacio de parametros (mapa de promedios en función de los parametros ) como se ve en la Fig. 1(a). El codigo de colores en el espacio de parámetros indica los promedios de la amplitud de cada patron espacio-temporal. Se puede observar una clara diferenciacion entre los distintos regímenes del sistema, ademas de presentar una simetría respecto a la diagonal que va de (-2,-2) a (2,2), a pesar de que en alguns casos, los patrones espacio-temporales son diferentes aunque parezca que la region en el espacio de parametros sea la misma (ver por ejemplo Fig. 1(b) y (c)). La region roja del mapa corresponde a regímenes laminares (Fig. 1(b)). Se distingue claramente que la region de inestabilidad está dividida en ocho partes: dos regiones de intermitencia donde predomina la laminaridad en una (Fig. 1(d)) y la turbulencia en la otra (Fig. 1(e)), zonas de color amarillo y verde respectivamente. Por otra parte, una region

 

 

dominada por la turbulencia mediada por defectos de color azul (Fig. 1(f)); y otra region dominada por una fuerte formacion de fuentes y sumideros (Fig. 1(g)) en el extremo del regimen intermitente próximo al valor cero del parametro de dispersión lineal . Finalmente, dos regiones de transicion de fase entre las regiones de laminaridad, intermitencia y turbulencia, zonas de color rojo claro (definida como la tur-

 

bulencia de fase que aparece en la Fig. 1(c)) y celeste, y dos regiones de transicion de fase entre la zona de fuentes y sumideros, y las regiones de intermitencia (Fig. 1(h) e (i));

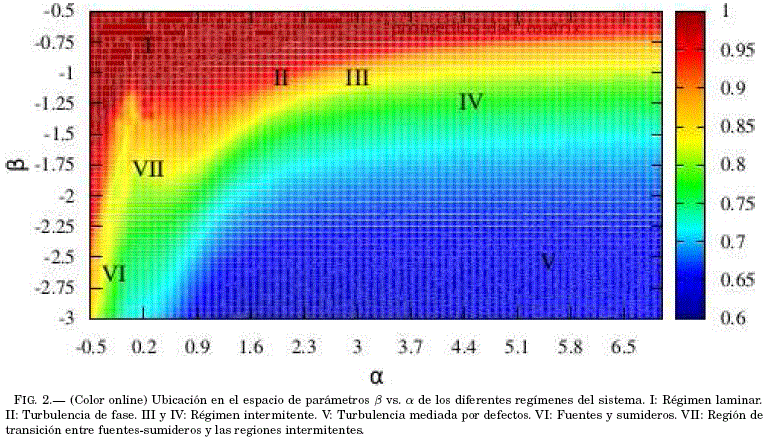
Finalmente, con el fin de tener un panorama mas amplio de las distintas regiones mencionadas, se magnifica el espacio de parametros, trabajando con el mismo paso de tiempo, para valores de en el intervalo [-0.5,7] con pasos de 0.05 y en el intervalo [-3, -0.5] con pasos de 0.08 (Fig. 2), mas allá de estos valores se presenta divergencia en las soluciones.

 

5. CONCLUSIONES Y PERSPECTIVAS

Despues de realizar un intenso trabajo numérico con el fin de poder distinguir entre los diferentes regímenes, se pudo construir el espacio de parametros que permite hacer una clara distincion de los comportamientos existentes, incluyendo las regiones de transicion de fase. Además, se pudo tambien observar una simetría respecto a la diagonal en terminos de los promedios y que la region correspondiente al régimen de turbulencia mediada por defectos es pequena comparada con la region de laminaridad.

Como perspectivas, se tiene previsto realizar un analisis más detallado del espacio de parámetros, en especial de la region de fuentes y sumideros; tambien se pretende tener una visión más amplia del regimen turbulento y su cuantificación mediante otras herramientas de la dinamica no lineal tales como el calculo de exponentes de Lyapunov y/o periodicidades; por otra parte, se buscaran otras formas de modelar el problema, por ejemplo usando sistemas multiagentes; por ultimo, se pretende observar el comportamiento del sistema frente a perturbaciones externas, así como estudiar situaciones que puedan ser aplicadas en el area de la física del estado solido.

 

Notas

^† dneutron.js@gmail.com

^‡ http://www.fiumsa.edu.bo/docentes/mramirez/

 

REFERENCIAS

Conway J. M. (2008), Complex Patterns in Oscillatory Systems. (Tesis doctoral - Northwestern University).         [ Links ]

Cox S. M. & Matthew P. C. (2002), Journal of Computational Physics 176, 430.         [ Links ]

Cross M. C. & Hohenberg P. C. (1993), Review ofModern Physics 65, 851.         [ Links ]

Geldhof S. (2013), Pseudoespectral Methods for a class of Evolutionary Systems. (Tesis doctoral - Colorado School of Mines).        [ Links ]

Nicolis G. (1995), Introduction to nonlinear science. (Cambridge University Press).        [ Links ]

Rabinovich M. I. Ezersky A. B. & Weidman P. D. (2000), The dynamics of patterns. (Singapur: World Scientific Publlishing).         [ Links ]

Turing A. M. (1952), The Chemical Basis of Morphogenesis. Philosophical Transactions ofthe Roy al Society ofLondon. Series B, Biological Sciences 237, 37.         [ Links ]

Walgraed D. & Ghoniem N M. Ed. (1990), Patterns, Defects and Materials Instabilities. (Dordrecht: Kluwer Academic Publishers).        [ Links ]