Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Boliviana de Física
versión On-line ISSN 1562-3823
Revista Boliviana de Física vol.27 no.27 La Paz dic. 2015
ARTÍCULOS
Análisis del plano de fases de un modelo discreto de neurona basado en la determinación de periodicidades
Phase plane analysis of a neuron map-based model by determining periodicities
G. M. Ramírez Ávila†
Instituto de Investigaciones Físicas, Carrera de Física
Universidad Mayor de San Andres
c. 27 Cota-Cota, Campus Universitario, Casilla de Correos 8635 La Paz - Bolivia
Marcia R. Gallas & Jason A. C. Gallas‡
Departamento de Física Universidade Federal da Paraíba
58051-970 Joao Pessoa, Brazil Instituto de Altos Estudos da Paraíba Rua Infante Dom
Henrique 100-180158039-150 Joao Pessoa, Brazil &
Institute for Multiscale Simulation Friedrich-Alexander Universitat Erlangen-Nürnberg 91052 Erlangen, Germany
(Recibido 10 de noviembre de 2015; aceptado 12 de diciembre de 2015)
Resumen
Se estudia el plano de fases del modelo de Rulkov, basado en un mapa bidimensional que describe el comportamiento de una neurona. Fijando un parametro de control de los tres en juego, se obtienen planos de fase mostrando las periodicidades definidas en ciertas regiones del mismo. Se muestra la importancia del parametro /x en la determinacion de las periodicidades y numero de picos por ráfaga, cantidades que además están ligadas por una relación lineal. Las zonas en las que estan definidas estas periodicidades muestran en algunos casos, patrones similares a los que se encuentran en los troncos y hojas de ciertas palmeras. La determinacion y descripción detallada de estas zonas de periodicidad puede constituirse en la base para un estudio de sincronizacion de neuronas no idénticas en regiones para las cuales los valores de los parametros nos garanticen trabajar con la misma periodicidad. Se analiza tambien la fiabilidad y limitaciones del método.
Codigo(s) PACS: 05.45.-a, 02.70.-c, 87.19.L-
Descriptores: Dinamica no lineal y caos Técnicas computacionales; simulaciones Neuro-ciencia.
Abstract
We study the Rulkov model phase plane, a two-dimensional map-based model that describes the behavior of a neuron. Keeping constant one of the three parameters, we obtain phase planes showing well-defined periodicities. We show the importance of the parameter \i identifying the periodicities and the number of spikes per burst, quantities that are related between them by a linear relationship. The zones in which these periodicities are well-defined exhibit in some cases, shapes similar to those appearing in some palm-tree patterns observed both in trunks and in leaves. The detailed determination and description of these periodicity zones could be the basis for a further study on synchronization of nonidentical neurons in regions in which the domain of the parameter values ensure the fact to work with the same periodicity. We also analyze the reliability and the limitations of this method.
Subject headings: Nonlinear dynamics and chaos Computational techniques; simulations Neuroscience.
1. INTRODUCCION
En los ultimos años, el estudio del cerebro ha cobrado un notorio interes no solamente en científicos relacionados con ciencias medicas y biológicas, sino tambien en físicos, matematicos, químicos e informaticos. El estudio inter, multi y transdisciplinar resultante es lo que se denomina neurociencia que es el estudio de la estructura y funcion del sistema nervioso como lo senala Purves (2010).
Las neuronas son las celulas que constituyen los bloques fundamentales para la funcionalidad cerebral. De acuerdo con Longstaff (2011), se estima que en el cerebro humano, se tienen 8.6 x1O10 neuronas, de las cuales 1.6 x 1010 estan en la corteza cerebral y 6.9 x1O10 en el cerebelo. Existen diferentes tipos de neuronas en el cerebro humano y una gran variedad en el cerebro de otras especies por lo que referirse a un modelo de neurona es una abstraccion que considera los aspectos claves de las neuronas sin pretender que el mismo pueda describir a cualquier neurona de la vasta variedad existentes, tal como lo indica Arbib (2003).
La utilizacion de ideas de dinámica no lineal en neurobiología radica en el hecho de tratar con sistemas de entrada/salida (input/output). Abarbanel & Rabinovich (2001) indican que los sistemas nerviosos reciben estímulos de su entorno y emplean secuencias de picos para transportar a traves de circuitos neuronales la informacion contenida en los estímulos. En estos circuitos, la informacion es procesada y distribuida para finalmente producir respuestas conducentes a actividades funcionales . Ademas, Izhikevich (2007) puntualiza que las neuronas en el cerebro, tambien se comunican entre si por secuencias de picos electricos o potenciales de acción; estos picos representan desde un punto de vista fisiologico, cambios abruptos en el potencial de membrana, el cual se propaga a otras neuronas a traves de una larga protuberancia denominada axon. Uno de los desafíos mayores de la neurociencia es el de entender los mecanismos fisiologicos básicos subyacentes a los complejos patrones espacio-temporales de la actividad proveniente de las secuencias de picos durante el funcionamiento normal del cerebro y para determinar los orígenes de estados dinamicos patológicos tales como ataques de epilepsia y temblores parkin-sonianos. Un segundo desafío es el de entender como estos patrones de actividad proporcionan un sustrato para la codificacion y transmisión de la información, esto es, tal como se cuestionan Coombes & Bressloff (2005), ¿como se analizan neuronas con picos o potenciales de accion?
Hoy en día, los aspectos computacionales han adquirido gran importancia en neurociencia ya sea para el estudio de transmision sináptica y la consecuente generacion de potenciales de acción, de la interaccion de neuronas en una red, de los procesos de alto nivel de percepcion y memoria. Los modelos computacionales ofrecen nuevas visiones de la maquinaria compleja en la que subyace el comportamiento. Estos modelos permiten aclarar el entendimiento de funciones y procesos en el sistema nervioso, ademas de otorgar el formalismo para expresar las hipotesis incluyendo todas las suposiciones en un marco conceptual coherente. Ademas, un modelo matematico por más simple que sea permite hacer predicciones que deben ser validadas por experimentos como lo expresa Cisek et al. (2007). El analisis de las ecuaciones de estos modelos ha resultado en tecnicas matemáticas sofisticadas en los campos de las ecuaciones diferenciales en derivadas parciales y en sistemas dinamicos en general; así, como lo expresa Borisyuk et al. (2005), el campo de la neurociencia computacional se considera ya como una disciplina bien establecida y que a veces se la denomina neurociencia teorica y que se integra al trabajo experimental. Tal integracion requiere visión clara en los procesos de informacion realizados por las estructuras del cerebro en los diferentes niveles como se establece en el trabajo de Coward (2013). La neurociencia abarca enfoques que van desde los estudios moleculares y celulares de psicofísica y psicología. La neurociencia teorica favorece el contacto entre estas subdisciplinas mediante la construccion de representaciones compactas de lo que se ha aprendido, construyendo puentes entre diferentes niveles de descripcion, y la identificación de los conceptos y principios unificadores tal como Dayan & Abbott (2001) lo indican. Nuevos campos aparecen, como la neurociencia cognitiva basada en modelos; esta se la define por una relacion recíproca entre la neurociencia cognitiva con el modelado matematico del comportamiento como lo senalan Forstmann & Wagen-makers (2015).
Como se menciono más arriba, el modelado de neuronas es esencial para el avance de la neurociencia. El modelo basado en ecuaciones diferenciales debido a Hodgkin & Huxley (1952), constituye el primer intento de describir el funcionamiento de una neurona, en particular, las respuestas de un axon aislado de calamar europeo (Loligo vulgaris) caracterizadas por variaciones del potencial de membrana debidas a estímulos electricos. Posteriormente, se formulan otros modelos tanto continuos como los debidos a FitzHugh (1961); Plant & Kim (1976); Hindmarsh & Rose (1984), como aquellos basados en mapas tales como los propuestos por Rulkov (2002); Chialvo (1995); Izhikevich & Hoppensteadt (2004); una revision de los modelos neuronales basados en mapas se puede encontrar en el trabajo de Ibarz et al. (2011).
El estudio de periodicidades en diferentes tipos de sistemas ha cobrado interes recientemente; así, el hallazgo de secuencias periodicas como los árboles de Stern-Brocot en sistemas excitables tales como el de FitzHugh-Nagumo o el de Bonhoeffer-van der Pol descrito por Freire & Gallas (2011b) o en sistemas químicos que describen la paradigmatica reaccion de Belousov-Zhabotinsky (BZ) estudiados por Freire & Gallas (2011a) (Oporto Almaraz & Ramírez Avila (2004) describen aspectos básicos de la reaccion BZ; posteriormente, Oporto Almaraz & Ramırez Ávila (2013) estudiaron aspectos no lineales de esta reaccion, tales como su estabilidad; y finalmente, su comportamiento sıncrono es analizado por Oporto Almaraz & Ramírez Avila (2014); estos trabajos fueron publicados en esta misma revista). Otros sistemas tales como circuitos electronicos mostrando oscilaciones antiperiodicas como los descritos por Freire et al. (2014); poblaciones celulares ligadas a la evolucion de cáncer analizadas por Gallas et al. (2014); o en reacciones bioquımicas oscilantes tales como las estudiadas por Gallas & Gallas (2015) han sido tambien objeto de la aplicación de análisis de periodicidades para su estudio. En un numero anterior de esta revista, habíamos resaltado el hecho de que los sistemas dinamicos, en particular aquellos representados por mapas eran susceptibles a ser analizados mediante periodicidades: uno de los sistemas escogidos fue el modelo de neurona debido a Rulkov (2002), en el cual encontramos regiones periodicas bien definidas en el espacio de parámetros comunmente considerados en el análisis de este modelo y mostrado por Ramírez Avila & Gallas (2011).
Este trabajo tiene como objetivo analizar un modelo de neurona en terminos de periodicidades y tambien el abrir la posibilidad de extender este tipo de analisis a situaciones realistas en las que se puedan estudiar redes neuronales conducentes a la realizacion de funciones específicas en el cerebro.
El artículo esta organizado de la siguiente manera: en §2, se introduce el modelo neuronal de Rulkov que constituye el sistema dinamico objeto de nuestro analisis. Los resultados del análisis de periodicidades para diferentes valores del parametro del control ii se dan en §3. Finalmente, en §4 se senalan las conclusiones y perspectivas de la presente investigacion.
2. MODELO
Como se indico en §1, el modelo de neurona que utilizamos en este trabajo es el de Rulkov, el cual esta formulado como:
![]()
donde
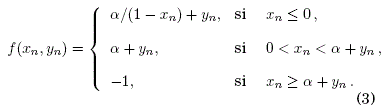
Siendo x y y las variables dinamicas rápida y lenta respectivamente y ![]() son parametros que caracterizan al sistema.
son parametros que caracterizan al sistema.
Los estudios correspondientes a este modelo consideran en general un valor pequeno para el parametro ![]() lo que garantiza una intensa actividad de secuencias de picos que como se indico en §1 constituye la forma en la cual se transmite y recibe informacion conducentes a la realización de una determinada accion. El valor tomado para
lo que garantiza una intensa actividad de secuencias de picos que como se indico en §1 constituye la forma en la cual se transmite y recibe informacion conducentes a la realización de una determinada accion. El valor tomado para ![]() es de 0.001 tal como lo hicieron Rulkov (2002) y Shilnikov & Rulkov (2003). El rol de
es de 0.001 tal como lo hicieron Rulkov (2002) y Shilnikov & Rulkov (2003). El rol de ![]() es el de identificar el voltaje de reinicializacion relativo a las ramas estables e inestables de la nulclina rapida; en tanto, el cambio en
es el de identificar el voltaje de reinicializacion relativo a las ramas estables e inestables de la nulclina rapida; en tanto, el cambio en ![]() desplaza la nulclina lenta de manera vertical en el plano de fases tal como lo senalan Ibarz et al. (2011). En todos los trabajos anteriormente citados, se destaca el hecho de escoger un valor pequeno para
desplaza la nulclina lenta de manera vertical en el plano de fases tal como lo senalan Ibarz et al. (2011). En todos los trabajos anteriormente citados, se destaca el hecho de escoger un valor pequeno para ![]() . Sin embargo, en este trabajo, pretendemos analizar que es lo que ocurre cuando se consideran otros valores para el parametro
. Sin embargo, en este trabajo, pretendemos analizar que es lo que ocurre cuando se consideran otros valores para el parametro ![]() , tanto menores como mayores. Para nuestro analisis, consideraremos siempre las mismas condiciones iniciales
, tanto menores como mayores. Para nuestro analisis, consideraremos siempre las mismas condiciones iniciales ![]() para cada uno de los experimentos numericos.
para cada uno de los experimentos numericos.
3. RESULTADOS
Para el analisis del modelo de Rulkov, primeramente fijamos el valor de los parametros ![]() = -0.459 y
= -0.459 y![]() = 12.0; con estos valores establecidos, se procede a variar el valor de
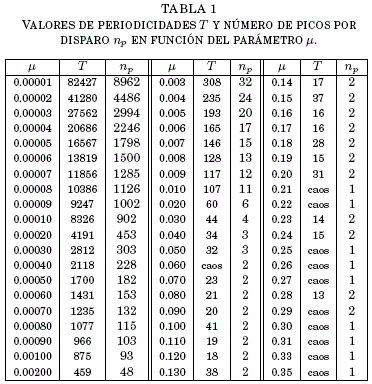
= 12.0; con estos valores establecidos, se procede a variar el valor de![]() en el intervalo [10-5,0.35] (ver Tabla 1). En estas condiciones, se obtienen las series temporales para las variables rápida
en el intervalo [10-5,0.35] (ver Tabla 1). En estas condiciones, se obtienen las series temporales para las variables rápida ![]() y lenta
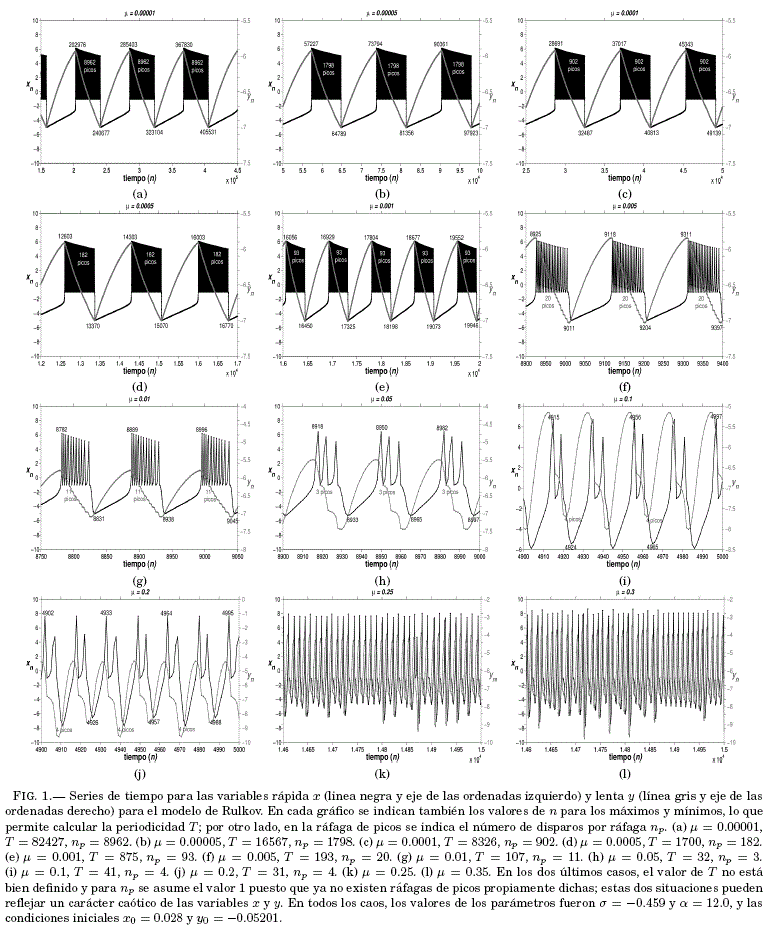
y lenta ![]() , las cuales estan representadas en la Fig. 1, cuyo análisis permite resaltar los siguientes aspectos a ser profundizados: (i) El estudio detallado en funcion del parametro
, las cuales estan representadas en la Fig. 1, cuyo análisis permite resaltar los siguientes aspectos a ser profundizados: (i) El estudio detallado en funcion del parametro![]() de periodicidades y del numero de picos en las rafagas cuando estas se presentan en la variable
de periodicidades y del numero de picos en las rafagas cuando estas se presentan en la variable ![]() (ver §3.1). (ii) La obtencion de espacios de parametros en el plano definido por los parámetros
(ver §3.1). (ii) La obtencion de espacios de parametros en el plano definido por los parámetros ![]() y
y![]() variando el valor de
variando el valor de ![]() en el mismo intervalo senalado anteriormente y caracterizados por el valor de las periodicidades (ver §3.2). (iii) La evaluacion de las ventajas y las limitaciones que presentan los espacios de parametros basados en el cálculo de las periodicidades y la comparacion con otros métodos como por ejemplo el espacio de parametros caracterizados por los mayores exponentes de Lyapunov (ver §3.3). Es conveniente aclarar que se entiende por periodicidad, el numero de pasos de tiempo
en el mismo intervalo senalado anteriormente y caracterizados por el valor de las periodicidades (ver §3.2). (iii) La evaluacion de las ventajas y las limitaciones que presentan los espacios de parametros basados en el cálculo de las periodicidades y la comparacion con otros métodos como por ejemplo el espacio de parametros caracterizados por los mayores exponentes de Lyapunov (ver §3.3). Es conveniente aclarar que se entiende por periodicidad, el numero de pasos de tiempo ![]() que transcurren hasta que la variable en cuestion alcance exactamente el mismo valor.
que transcurren hasta que la variable en cuestion alcance exactamente el mismo valor.
3.1. Ráfagas de picos y periodicidades
Una inspeccion más profunda de la Fig. 1 permite observar que la forma de las series temporales de las variables ![]() e
e ![]() parecen ser bastante diferentes entre si; así, la variable dinámica rápida
parecen ser bastante diferentes entre si; así, la variable dinámica rápida ![]() para la mayor parte de los valores de
para la mayor parte de los valores de ![]() presenta rafagas de picos; en tanto que la variable lenta
presenta rafagas de picos; en tanto que la variable lenta ![]() presenta senales típicas de una oscilacion de relajación que como es bien sabido se caracteriza por no ser senoidal como lo senala Eggleston (2011). A pesar de la gran diferencia en forma de las senales de
presenta senales típicas de una oscilacion de relajación que como es bien sabido se caracteriza por no ser senoidal como lo senala Eggleston (2011). A pesar de la gran diferencia en forma de las senales de ![]() e
e ![]() , la periodicidad para ambas tiende a ser la misma.
, la periodicidad para ambas tiende a ser la misma.
Para valores pequenos de ![]() , se tiene una gran actividad en los potenciales de accion de la neurona, manifestada por el gran numero de picos por ráfaga
, se tiene una gran actividad en los potenciales de accion de la neurona, manifestada por el gran numero de picos por ráfaga ![]() y por grandes valores en la periodicidad de las variables
y por grandes valores en la periodicidad de las variables ![]() que ademas coinciden en su valor por lo que podríamos escribir genericamente
que ademas coinciden en su valor por lo que podríamos escribir genericamente ![]() Así, en la Fig. 1(a) con
Así, en la Fig. 1(a) con ![]() = lO-5, se
= lO-5, se
tienen 8962 picos por rafaga y una periodicidad de 82427. A medida que aumenta el valor de ![]() , tanto
, tanto![]() como
como ![]() disminuyen dramaticamente tal como muestran los valores de la Tabla 1. Es interesante ver que la senal de la variable
disminuyen dramaticamente tal como muestran los valores de la Tabla 1. Es interesante ver que la senal de la variable ![]() mantiene completamente su forma de oscilacion de relajación (Figs. 1(a)-(e)) hasta el valor aproximado de
mantiene completamente su forma de oscilacion de relajación (Figs. 1(a)-(e)) hasta el valor aproximado de ![]() = 0.01 (Fig. 1(g)) donde aparecen pequenas deformaciones en la señal. Para valores mayores de
= 0.01 (Fig. 1(g)) donde aparecen pequenas deformaciones en la señal. Para valores mayores de ![]() , se nota que la tendencia de la senal de
, se nota que la tendencia de la senal de ![]() es a suavizarse perdiendo su caracter de relajacion (Fig. 1(h)-(j)). Finalmente, para valores mayores de
es a suavizarse perdiendo su caracter de relajacion (Fig. 1(h)-(j)). Finalmente, para valores mayores de ![]() ; a partir de
; a partir de ![]() = 0.21, en la mayorıa de las situaciones que se presentan no se puede determinar el valor de
= 0.21, en la mayorıa de las situaciones que se presentan no se puede determinar el valor de ![]() lo que indica que en estos casos se tienen comportamientos caoticos para las series temporales asociadas a las variables
lo que indica que en estos casos se tienen comportamientos caoticos para las series temporales asociadas a las variables ![]() e
e ![]() (Fig. 1(k)-(l)).
(Fig. 1(k)-(l)).
Utilizando los datos de la Tabla 1 se hace una representacion log-log tanto de ![]() como
como ![]() en funcion de
en funcion de ![]() como se muestra en la Fig. 2(a)-(b) donde se nota inmediatamente que se esta frente a situaciones que siguen leyes de potencia de la forma:
como se muestra en la Fig. 2(a)-(b) donde se nota inmediatamente que se esta frente a situaciones que siguen leyes de potencia de la forma:
![]()
donde los coeficientes se calcularon con un umbral de confianza del 95%, siendo sus valores:
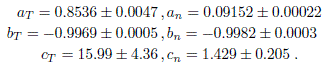
No es sorprendente encontrar este tipo de comportamiento puesto que sistemas que obedecen este tipo de leyes estan omnipresentes en la naturaleza. Cuando la probabilidad de medir un valor particular de alguna magnitud varía inversamente como una potencia de este valor, se dice que la magnitud sigue una ley de potencia como lo expresa Newman (2005). En terminos más simples, una ley de potencia es un modelo matematico que describe una relacion dinámica entre dos objetos; habiendo una gran cantidad de ejemplos en sistemas naturales y artificiales; ademas de estar ligada a fenómenos tales como las transiciones de fase en materiales ferro-magneticos revisadas por Lucano Lucano & Ramírez Avila (2012) o en numerosos ejemplos que se mencionan en Novak (2002) tales como aquellos relacionados con series de tiempo fisiologicas, con distribuciones de poblaciones, con series temporales fi-
nancieras, o con fısica de partículas entre otros; o en los tratados por Ghosh (2011), donde se hace enfasis en ejemplos geométricos y mecánicos que tienen como objetivo el explicar y aplicar procesos de miniaturizacion como lo explican en detalle Ghosh & Corves (2015). Todas estas leyes de potencia tienen como característica principal el denominado exponente crítico que varía de acuerdo a los sistemas considerados. En nuestro caso, se observa que el exponente crítico ligado a la periodicidad ![]() es practicamente igual a aquel relacionado con el numero de picos por ráfaga
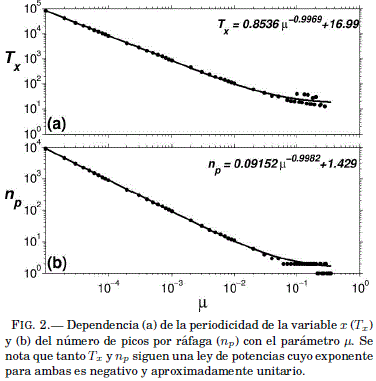
es practicamente igual a aquel relacionado con el numero de picos por ráfaga ![]() lo que nos muestra que estos fenomenos están estrechamente relacionados entre sı y que se corrobora en la Fig. 3, donde se tiene una dependencia lineal entre
lo que nos muestra que estos fenomenos están estrechamente relacionados entre sı y que se corrobora en la Fig. 3, donde se tiene una dependencia lineal entre ![]() y
y ![]() de la forma:
de la forma:
![]()
donde ![]() calculados con un umbral de confianza de 95%.
calculados con un umbral de confianza de 95%.
Para terminar este apartado, resaltamos el hecho de la estrecha relacion entre ![]() y
y ![]() lo que, en principio, para el analisis dinámico del modelo podríamos considerar cualquiera de estas cantidades; sin embargo, como se pudo constatar a partir de lo expuesto anteriormente,
lo que, en principio, para el analisis dinámico del modelo podríamos considerar cualquiera de estas cantidades; sin embargo, como se pudo constatar a partir de lo expuesto anteriormente, ![]() solo se presenta en
solo se presenta en ![]() por lo que el analisis sólo sería para esta variable. En contraposicion, cuando el análisis se lo realiza mediante periodicidades, se nota que es practicamente indistinto considerar una u otra variable como se vera en §3.2.
por lo que el analisis sólo sería para esta variable. En contraposicion, cuando el análisis se lo realiza mediante periodicidades, se nota que es practicamente indistinto considerar una u otra variable como se vera en §3.2.
3.2. Periodicidades en el espacio de parámetros
Como se indico al final de §3.1, elegimos s las periodicidades para caracterizar el sistema dinamico correspondiente al modelo de Rulkov. Para tal efecto, se procede a obtener los espacios de parametros ![]() vs.
vs. ![]() en la region comprendida en los intervalos
en la region comprendida en los intervalos ![]() = [4,4] y
= [4,4] y ![]() = [-10, 20] considerando la periodicidad
= [-10, 20] considerando la periodicidad ![]() =
= ![]() como la cantidad que caracteriza a estos espacios de parametros, siendo
como la cantidad que caracteriza a estos espacios de parametros, siendo ![]() = 5000 que se elige como valor maximo de periodicidad que se computa en nuestros experimentos numericos de. Se trabaja con los mismos valores del parametro
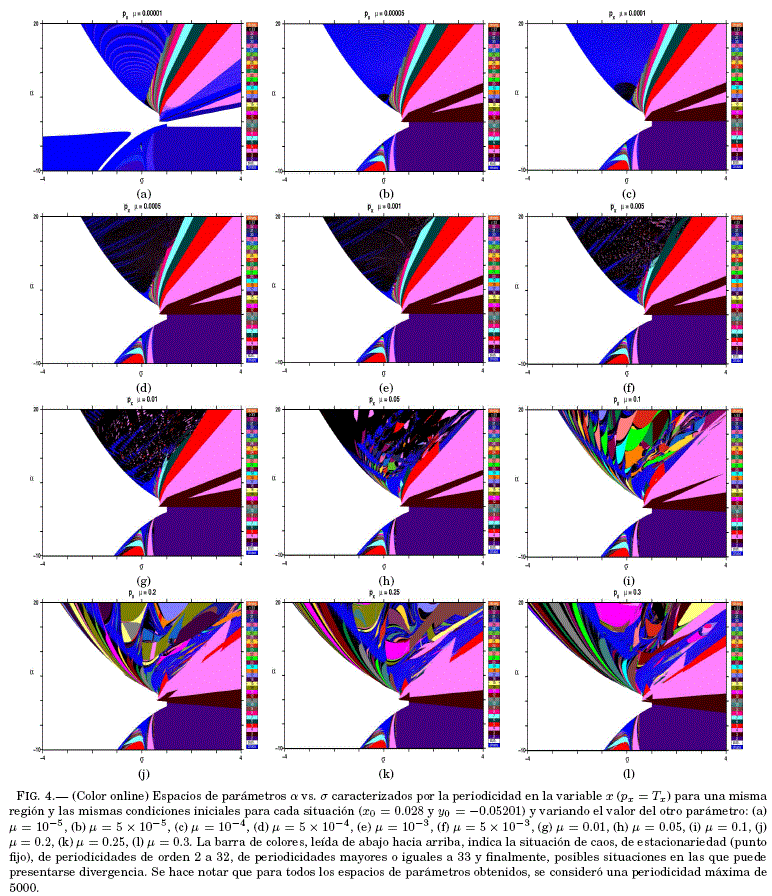
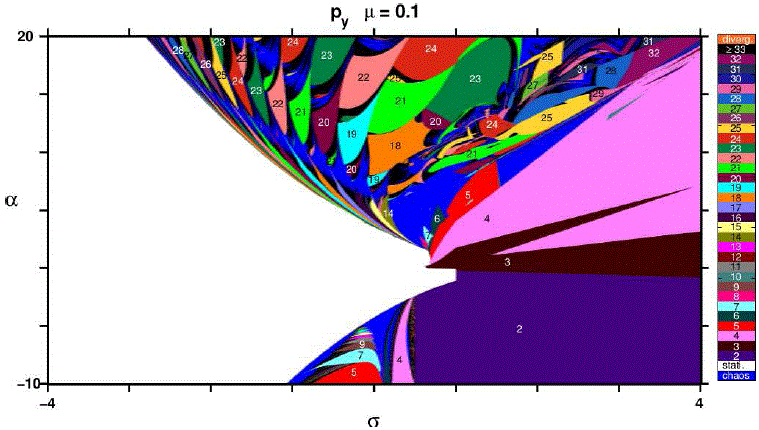
= 5000 que se elige como valor maximo de periodicidad que se computa en nuestros experimentos numericos de. Se trabaja con los mismos valores del parametro ![]() que se usaron en la Fig. 1 así como las mismas condiciones iniciales senaladas en §2. Estos espacios de parametros se muestran en la Fig. 4, donde en cada uno de ellos se identifican regiones tıpicas tales como las representadas en blanco que indican la existencia de puntos fijos (desde la parte central hasta la izquierda en su totalidad), rubrica de que no se tienen oscilaciones en las variables
que se usaron en la Fig. 1 así como las mismas condiciones iniciales senaladas en §2. Estos espacios de parametros se muestran en la Fig. 4, donde en cada uno de ellos se identifican regiones tıpicas tales como las representadas en blanco que indican la existencia de puntos fijos (desde la parte central hasta la izquierda en su totalidad), rubrica de que no se tienen oscilaciones en las variables ![]() e
e ![]() ; tambien para valores que van de la parte central hasta la integridad de la parte derecha en, donde las periodicidades son en general pequenas y con pequeñas regiones caóticas en la parte inferior-central; finalmente, se tiene otra region en forma de triángulo esférico ubicada desde la parte central y extendiendose a la parte superior, la cual merecera especial atención para su análisis puesto que es en esta zona en la cual se presentan los comportamientos dinamicos más interesantes, tales como la existencia de rafagas de picos en la variable
; tambien para valores que van de la parte central hasta la integridad de la parte derecha en, donde las periodicidades son en general pequenas y con pequeñas regiones caóticas en la parte inferior-central; finalmente, se tiene otra region en forma de triángulo esférico ubicada desde la parte central y extendiendose a la parte superior, la cual merecera especial atención para su análisis puesto que es en esta zona en la cual se presentan los comportamientos dinamicos más interesantes, tales como la existencia de rafagas de picos en la variable ![]() y la formacion de interesantes patrones de periodicidad como se vera más adelante; por esta razón, en lo que sigue la denominaremos region de interés (RI). Para valores pequenos de
y la formacion de interesantes patrones de periodicidad como se vera más adelante; por esta razón, en lo que sigue la denominaremos region de interés (RI). Para valores pequenos de ![]() se nota una predominancia de comportamiento caotico en la RI (Fig. 4(a)-(c)) que como veremos mas adelante no es más que una mala interpretacion de los resultados que se aclarará en §3.3. Para valores ligeramente mayores de
se nota una predominancia de comportamiento caotico en la RI (Fig. 4(a)-(c)) que como veremos mas adelante no es más que una mala interpretacion de los resultados que se aclarará en §3.3. Para valores ligeramente mayores de ![]() en el intervalo [5, 50] x 10-4, se tienen en la RI, zonas predominantes de periodicidades
en el intervalo [5, 50] x 10-4, se tienen en la RI, zonas predominantes de periodicidades ![]() 33 intercaladas con zonas caoticas (Fig. 4(d)-(f)). Para valores aun mayores de
33 intercaladas con zonas caoticas (Fig. 4(d)-(f)). Para valores aun mayores de ![]() en el intervalo [0.01,0.05], se nota que en la RI aparecen pequenas zonas periódicas (Fig. 4(g)-(h)) que se ven consolidadas en la Fig. 4(i) cuyo detalle fino en cuanto a valores de periodicidad se muestra en la Fig. 5(a), donde se notan patrones de periodicidad bien definidos en la parte central de la RI y que son similares a los patrones que se observan en troncos de ciertas especies de palmera (Fig. 5(b)); en tanto que la parte contigua al borde izquierdo de la RI exhibe patrones periodicos que tienen la forma del follaje tambien de palmeras (Fig. 5(c)); justamente con este valor de parametro
en el intervalo [0.01,0.05], se nota que en la RI aparecen pequenas zonas periódicas (Fig. 4(g)-(h)) que se ven consolidadas en la Fig. 4(i) cuyo detalle fino en cuanto a valores de periodicidad se muestra en la Fig. 5(a), donde se notan patrones de periodicidad bien definidos en la parte central de la RI y que son similares a los patrones que se observan en troncos de ciertas especies de palmera (Fig. 5(b)); en tanto que la parte contigua al borde izquierdo de la RI exhibe patrones periodicos que tienen la forma del follaje tambien de palmeras (Fig. 5(c)); justamente con este valor de parametro ![]() = 0.1 pero para la periodicidad en la variable
= 0.1 pero para la periodicidad en la variable ![]() (Fig. 5) se explica con mayor claridad el codigo de colores mostrado en las figuras de los espacios de parametros basados en la periodicidad. Finalmente, en la Fig. 4(j)-(l), para valores de
(Fig. 5) se explica con mayor claridad el codigo de colores mostrado en las figuras de los espacios de parametros basados en la periodicidad. Finalmente, en la Fig. 4(j)-(l), para valores de ![]() comprendidos entre 0.2 y 0.3, se nota que el patron tipo follaje de palmera en la RI se torna mas evidente. Se puede ver tambien que existen ciertas regularidades en lo que concierne a la secuencia de periodicidades; así, se nota en la parte central de la RI sucesiones que van de derecha a izquierda para las zonas de mayor area:
comprendidos entre 0.2 y 0.3, se nota que el patron tipo follaje de palmera en la RI se torna mas evidente. Se puede ver tambien que existen ciertas regularidades en lo que concierne a la secuencia de periodicidades; así, se nota en la parte central de la RI sucesiones que van de derecha a izquierda para las zonas de mayor area:
![]()
3.3. Ventajas y limitaciones del uso de periodicidades
Ası mismo, se puede señalar que el método utilizado de analisis de periodicidades en el espacio de parametros, tiene muchas ventajas, entre las cuales se pueden mencionar: (i) Permite conocer la dinamica del sistema de manera completa; es decir, no solo distinguir el comportamiento regular del caotico como se lo puede hacer utilizando el máximo exponente de Lyapunov sino tambien caracterizar el comportamiento regular diferenciando los puntos fijos de las periodicidades de diferente orden. (ii) Permite la identificacion de patrones en las estructuras que denotan periodicidades. (iii) Permite estudiar los tipos de bifurcaciones que se presentan en el sistema dinamico. (iv) Desde el punto de vista computacional, es menos costoso en tiempo obtener periodicidades que exponentes de Lyapunov. Empero, este metodo tambien presenta algunas limitaciones que se manifiestan especialmente, en el caso concreto que estudiamos, cuando los valores de ![]() son pequenos. Por ejemplo, consideremos el espacio de parametros para el valor de
son pequenos. Por ejemplo, consideremos el espacio de parametros para el valor de ![]() = 0.0001 (Fig. 4(c)), donde se ve claramente que la RI parece ser caotica casi en su totalidad. Sin embargo, si se consideran las series de tiempo de
= 0.0001 (Fig. 4(c)), donde se ve claramente que la RI parece ser caotica casi en su totalidad. Sin embargo, si se consideran las series de tiempo de ![]() y
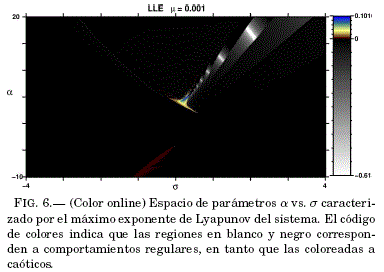
y ![]() mostradas en la (Fig. 1(c)) se ve que la periodicidad es de 8326, lo que contradice a lo que se muestra en el plano de fases con base en la periodicidad; por otra parte, el plano de fases construido a partir del maximo exponente de Lyapunov (Fig. 6) muestra que en efecto, la RI es predominantemente periodica. Lo anterior muestra que para la obtención de los planos de fase se debe tener mucho cuidado al calcular las periodicidades. En general, es inusual tener periodicidades relevantes mayores a 5000, es por eso que para los espacios de parametros de la Fig. 4 se había considerado este valor de 5000 como maximo, aunque, como se acaba de mencionar no es suficiente este criterio y para la obtencion adecuada de los espacios de parametros con base en las periodicidades, se tendra que explorar previamente el sistema para así poder trabajar con los valores adecuados para el calculo de dichas periodicidades.
mostradas en la (Fig. 1(c)) se ve que la periodicidad es de 8326, lo que contradice a lo que se muestra en el plano de fases con base en la periodicidad; por otra parte, el plano de fases construido a partir del maximo exponente de Lyapunov (Fig. 6) muestra que en efecto, la RI es predominantemente periodica. Lo anterior muestra que para la obtención de los planos de fase se debe tener mucho cuidado al calcular las periodicidades. En general, es inusual tener periodicidades relevantes mayores a 5000, es por eso que para los espacios de parametros de la Fig. 4 se había considerado este valor de 5000 como maximo, aunque, como se acaba de mencionar no es suficiente este criterio y para la obtencion adecuada de los espacios de parametros con base en las periodicidades, se tendra que explorar previamente el sistema para así poder trabajar con los valores adecuados para el calculo de dichas periodicidades.
4. CONCLUSIONES Y PERSPECTIVAS
El analisis detallado del modelo de neurona de Rulkov nos muestra interesantes aspectos tales como el hecho de que el parametro ![]() juega un rol muy importante en la determinacion de la periodicidad y del numero de picos por ráfaga. Como se vio, el aumento del valor de
juega un rol muy importante en la determinacion de la periodicidad y del numero de picos por ráfaga. Como se vio, el aumento del valor de ![]() hace que las periodicidades puedan variar desde cantidades del orden de cientos de miles hasta valores tan pequenos como 2 (ciclo de orden 2); similarmente, el numero de picos por rafaga para la variable rápida
hace que las periodicidades puedan variar desde cantidades del orden de cientos de miles hasta valores tan pequenos como 2 (ciclo de orden 2); similarmente, el numero de picos por rafaga para la variable rápida ![]() varía tambien con este aumento entre un numero del orden de decena de miles hasta 2. Desde el punto de vista de la neurociencia, este numero es quizás uno de los aspectos mas importantes del modelo puesto que tiene una relacion directa con los aspectos fisiológicos de la neurona y la funcionalidad de la misma. No obstante, desde una perspectiva de sistemas dinamicos, la periodicidad se presenta como una característica mas
varía tambien con este aumento entre un numero del orden de decena de miles hasta 2. Desde el punto de vista de la neurociencia, este numero es quizás uno de los aspectos mas importantes del modelo puesto que tiene una relacion directa con los aspectos fisiológicos de la neurona y la funcionalidad de la misma. No obstante, desde una perspectiva de sistemas dinamicos, la periodicidad se presenta como una característica mas
interesante para el sistema, por lo que cualquiera de las dos variables ![]() o
o ![]() puede ser utilizada para la descripcion del mismo; siendo incluso la variable lenta
puede ser utilizada para la descripcion del mismo; siendo incluso la variable lenta ![]() mas apropiada para determinar periodicidades. Hacemos notar que en general, los valores de periodicidad calculados utilizando cualesquiera de las variables coincide. Se observa tambien que para valores grandes de
mas apropiada para determinar periodicidades. Hacemos notar que en general, los valores de periodicidad calculados utilizando cualesquiera de las variables coincide. Se observa tambien que para valores grandes de ![]() , los comportamientos caoticos del sistema son mas probables. Es interesante notar que para los valores escogidos de los parametros, la periodicidad y el numero de picos por ráfaga están relacionados linealmente. El analisis de los espacios de parametros basados en la periodicidad nuestra que los mismos son muy dependientes del valor de
, los comportamientos caoticos del sistema son mas probables. Es interesante notar que para los valores escogidos de los parametros, la periodicidad y el numero de picos por ráfaga están relacionados linealmente. El analisis de los espacios de parametros basados en la periodicidad nuestra que los mismos son muy dependientes del valor de ![]() , especialmente en la region que denominamos RI. Para valores crecientes de
, especialmente en la region que denominamos RI. Para valores crecientes de ![]() aparecen zonas de periodicidad que en algunos casos muestran estructuras tales como los patrones que se observan en troncos y follaje de palmeras. Destacamos el hecho que el analisis basado en periodicidades comparado a aquel basado en exponentes de Lyapunov presenta varias ventajas, tales como la de brindar mayor informacion desde el punto de vista dinámico, y la de ser menos costoso computacionalmente hablando; sin embargo, tambien tiene limitaciones y requiere de ciertas precauciones en su uso, tales como el hecho de explorar previamente el sistema en cuestion para ası poder determinar los valores adecuados para los que se considerara el máximo de periodicidad; caso contrario, se corre el riesgo de obtener resultados falsos. La complementariedad de periodicidades y exponentes de Lyapunov puede ser muy util para el analisis de sistemas dinámicos dadas las virtudes y limitaciones que ofrecen ambos metodos.
aparecen zonas de periodicidad que en algunos casos muestran estructuras tales como los patrones que se observan en troncos y follaje de palmeras. Destacamos el hecho que el analisis basado en periodicidades comparado a aquel basado en exponentes de Lyapunov presenta varias ventajas, tales como la de brindar mayor informacion desde el punto de vista dinámico, y la de ser menos costoso computacionalmente hablando; sin embargo, tambien tiene limitaciones y requiere de ciertas precauciones en su uso, tales como el hecho de explorar previamente el sistema en cuestion para ası poder determinar los valores adecuados para los que se considerara el máximo de periodicidad; caso contrario, se corre el riesgo de obtener resultados falsos. La complementariedad de periodicidades y exponentes de Lyapunov puede ser muy util para el analisis de sistemas dinámicos dadas las virtudes y limitaciones que ofrecen ambos metodos.
Los resultados obtenidos, nos muestran la gran riqueza dinamica del modelo de Rulkov, en el cual existen muchos aspectos que todavía pueden ser explorados tales como el estudio de las bifurcaciones, las dependencias entre periodicidades y numero de picos por rafaga para otros valores de los parámetros, el estudio de los patrones que presentan las zonas de periodicidad, entre otros.
Notas
† http://www.fiumsa.edu.bo/docentes/mramirez/
‡ http://www.fisica.ufpb.br/jgallas/
AGRADECIMIENTOS
G.M.R.A. agradece al Prof. Juergen Kurths del Potsdam Institute for Climate Impact (PIK-Potsdam) por la invitacion científica a su institucion, tiempo en el cual parte de este trabajo fue desarrollado. Agradecemos tambien a la Dra. Mónica Moraes del Herbario Nacional de Bolivia por su colaboracion en lo concerniente a los detalles de palmeras y por permitirnos utilizar sus imagenes de estos vegetales.
REFERENCIAS
Abarbanel H. D. I. & Rabinovich M. I. (2001), Current Opinion in Neurobiology 11, 423. [ Links ]
Arbib M. A. (2003), The handbook ofbrain theory and neural net-works, 2nd edn. (Masachusetts: MIT Press). [ Links ]
Borisyuk A., Friedman A., Ermentrout B. & Terman D. (2005), Mathematical neuroscience (Berlín: Springer-Verlag). [ Links ]
Chialvo D. R. (1995), Chaos, Solitons & Fractals 5, 461. [ Links ]
Cisek P., Drew T. & Kalaska J. F. (2007), Computational neuroscience: theoretical insights into brain functions (Amsterdam: Elsevier). [ Links ]
Coombes S. & Bressloff R C. (2005), Bursting: The Genesis of Rhythm in the Nervous System (Singapore: World Scientific Publishing). [ Links ]
Coward L. A. (2013), Towards a Theoretical Neuroscience: from Cell Chemistry to Cognition (Dordrecht: Springer), 443. [ Links ]
Dayan P. & Abbott L. (2001), Theoretical Neuroscience (London: MIT Press), 460. [ Links ]
Eggleston D. L. (2011), Basic Electronics for Scientists and Engi-neers (New York: Cambridge University Press), 251. [ Links ]
FitzHugh R. (1961), Biophysical Journal 1, 445. [ Links ]
Forstmann B. U. & Wagenmakers E. J. (2015), An introduction to model-based cognitive (New York: Springer). [ Links ]
Freire J. G., Cabeza C., Marti A. C., Poschel T. & Gallas J. A. C. (2014), European Physical Journal: Special Topics 223, 2857. [ Links ]
Freire J. G. & Gallas J. A. C. (2011) a, Physical Chemistry Chemical Physics 13, 12191.
. (2011)b, Physics Letters A 375, 1097.
Gallas M. R., Gallas M. R. & Gallas J. A. C. (2015), European Physical Journal: Special Topics 223, 2131. [ Links ]
Gallas M. R. & Gallas J. A. C. (2015), Chaos: An Interdisciplinary Journal ofNonlinear Science 25, 064603. [ Links ]
Ghosh A. (2011), Scaling Laws, in Chakraborty, S. Ed., Mechanics Over Micro and Nano Scales (New York: Springer), 61. [ Links ]
Ghosh A. & Corves B. (2015), Introduction to Micromechanisms and Microactuators (New Delhi: Springer India), 161. [ Links ]
Hindmarsh J. L. & Rose R. M. (1984), Proceedings of the Royal Society of London. Series B. Biological Sciences 221, 87. [ Links ]
Hodgkin A. L. & Huxley A. F. (1952), Journal of Physiology 117, 500. [ Links ]
Ibarz B., Casado J. M. & Sanjuan M. A. F. (2011), Physics Reports 501, 1. [ Links ]
Izhikevich E. (2007), Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting (Cambridge: MIT Press), 505. [ Links ]
Izhikevich E. M. & Hoppensteadt F. (2004), International Journal of Bifurcation and Chaos 14, 3847. [ Links ]
Longstaff A. (2011), Instant Notes in Neuroscience (New York: Garland Science), 379. [ Links ]
Lucano Lucano M. J. & Ramírez Avila G. M. (2012), Copérnico 1,3. [ Links ]
Newman M. E. J. (2005), Contemporary Physics 46, 323. [ Links ]
Novak M. M. Ed. (2007), Emergent Nature: Pattern, Growth and Scaling in the Sciences (World Scientific Publishing Company), 44. [ Links ]
Oporto Almaraz S. A. & Ramırez Ávila G. M. (2004), Revista Boliviana de Física 10, 45.
. (2013), Revista Boliviana de Física 23, 16.
. (2014), Revista Boliviana de Física 25, 7.
Plant R. E. & Kim M. (1976), Biophysical Journal 16, 227. [ Links ]
Purves D. (2010), Brains. How they seem to work (Pearson Education, Inc.), 294. [ Links ]
Ramírez Avila G. M. & Gallas J. A. C. (2011), Revista Boliviana de Física 19, 1. [ Links ]
Rulkov N F. (2002), Physical Review E 65, 041922. [ Links ]
Shilnikov A. L. & Rulkov N F. (2003), International Journal of Bifurcation and Chaos 13, 3325. [ Links ]