FENÓMENOS NO LINEALES EN LA REACCIÓN
DE BELOUSOV - ZHABOTINSKY. ESTABILIDAD.

NON-LINEAR PHENOMENA OF THE
BELOUSOV - ZHABOTINSKY REACTION. STABILITY.

 

S. A. Oporto Almaraz^f ;G. M. Ramírez Ávila^f

 

---

Abstract

Empleando las ecuaciones diferenciales no-lineales del Oregonator como modelo de la dinámica de la reacción de Belousov-Zhabotinsky, se clasificaron los puntos fijos con carácter reactivo en el espacio de parámetros, obteniéndose una región de estabilidad respecto a un estado estacionario y otra de inestabilidad respecto a un ciclo límite; además, se obtuvo la curva de bifurcación de Hopf entre ambos regímenes, la cual depende de un parámetro de control asociado a la acidez de la solución. Adicionalmente al análisis teórico, realizamos experimentos en los que se obtuvo una distribución de puntos en el espacio de concentraciones semejante a la predicha por el Oregonator en el espacio de parámetros además de un margen que tiene el mismo significado que la curva de bifurcación. También se verificó la variación de dicho margen respecto a la acidez de la solución. Otro tipo de puntos fijos tienen carácter no-reactivo en tanto las especies químicas que dan lugar a la reacción no se pongan en contacto. El grado de concordancia entre el modelo y el experimento permite considerar la importancia del Oregonator de dos variables, aproximación que en general da resultados satisfactorios.

Código(s) PACS: 05.45.-a, 82.40.Bj, 82.40.Qt

Descriptores: Dinámica no lineal - Reacciones químicas - Oscilaciones y bifurcaciones en fisicoquímica - Sistemas químicos complejos.

Using the nonlinear differential equations of the Oregonator model to explain the Belousov-Zhabotinsky reaction, we classify the reactive fixed points into the parameter space. We obtain a stability region and an unstabilty one referred to a steady state and a limit cycle respectively; a Hopf bifurcation curve is established between both regions. This curve depends on a control parameter related to the acidity of the solution. Additionally to the theoretical analysis, we carried out experiments showing that the parameter space related to the concentrations is similar to that predicted by the Oregonator; and also an edge that has the same meaning as the bifurcation curve. We verify the dependence of this edge with the solution acidity. Other fixed points have a nonreactive feature while the reagents are not mixed. The agreement between the results from the model and the experiment gives rise to consider the importance of the Oregonator with two variables, approximation that gives, in general, satisfactory results.

Subject headings: Nonlinear dynamics - Chemical reactions - Oscillations, chaos, and bifurcations - Complex chemical systems

 

---

1  Introducción

Entre los fenómenos químicos complejos más representativos desde el punto de vista teórico y experimental se encuentra la reacción de Belousov-Zhabotinsky (BZ) que en su forma más difundida consiste en la oxidación de ácido malónico por iones bromato catalizada por iones de cerio en medio ácido, tal como se presenta por ejemplo en [11972Field et al.Field, Körös, & Noyes], en [22007Zhabotinsky ] y en [31994Gray & Scott]. Se considera que esta reacción se lleva a cabo a través de dos conjuntos de procesos inorgánicos monótonos alternados gracias a un tercer conjunto de reacciones orgánicas, lo que a escala macroscópica significa la variación en la concentración de determinadas especies químicas en forma de oscilaciones en medio homogéneo o formando patrones en medio heterogéneo (ver por ejemplo [42004Oporto Almaraz & Ramírez Ávila]).

La importancia de la reacción BZ radica en que esta constituye el modelo de algunos fenómenos biológicos como el proceso de emisión de señales celulares durante la autoorganización de Dictyostelium Discoideum descrito en [51994Goldbeter], la actividad tridimensional del ventrículo del corazón mencionada en [62002Murray] y el crecimiento periódico de liquen seg´un [71985Volkenshtein].

Field, Körös y Noyes llevaron a cabo el análisis cinético que condujo al mecanismo FKN, expuesto en [11972Field et al.Field, Körös, & Noyes], y a partir de este, [81974Field & Noyes] propusieron un modelo simplificado irreversible de cinco etapas y tres variables conocido como Oregonator, que conserva la no linealidad de la reacción BZ en grado tal que es capaz de reproducir oscilaciones periódicas y estados estacionarios. Trabajos posteriores reportan una mayor riqueza dinámica ya sea en reactor cerrado (ver [11972Field et al.Field, Körös, & Noyes]; [91992Ruoff]; [101997Johnson et al. Johnson, Scott & Thompson]) o con flujo de sustancia (en [111987Argoul et al. Argoul, Arneodo, Richetti & Roux]; [121981Hudson & Mankin]; [131980Janz et al., Janz, Vanecek & Field]; [141981Kepper & Boissonade]; [151991Schneider & Münster]) y mecanismos de hasta 80 etapas elementales, según lo expuesto por [161990Györgyi et al. Györgyi, Turángy & Field], que incluyen al Oregonator y con base en los cuales puede reproducirse satisfactoriamente la dinámica compleja de la reacción BZ (por ejemplo, su configuración permanente sobre un atractor extraño) tal como se describe en la secuencia de artículos: [171991Györgyi et al. Györgyi, Rempe & Field]; [181991Györgyi & Field]; [191992Györgyi et al. Györgyi, Field, Noszticzius, McCormick & Swinney]; [201992Györgyi & Field]. Con base en esta última referencia, un trabajo más elaborado desde el punto de vista numérico es el de [212011Freire & Gallas Freire & Gallas] en el que se investiga un modelo no polinomial de BZ de tres variables con 14 parámetros, incluido el flujo de sustancia, obteniéndose la distribución de modos de oscilación mixtos. Sin embargo, en estos casos la demanda analítica y numérica puede ser mayor y no suele traducirse en la clasificación de la dinámica en el espacio de parámetros. Así, para un sistema de flujo contínuo, dependiendo del valor de la velocidad de flujo de sustancia, estos modelos predicen ventanas caóticas alternadas con regiones periódicas aunque no se tiene conocimiento si el Oregonator describe la región de periodo simple. La validez de un modelo no es un problema teórico sino práctico de modo que el objetivo del trabajo reportado en este artículo es llevar a cabo la reacción BZ en reactor cerrado para verificar de forma cualitativa el alcance de las predicciones hechas por el Oregonator, aspecto importante considerando la relativa simplicidad de este modelo. También, el estudio analítico y numérico de fenómenos de mayor complejidad conduce a plantear la significancia del Oregonator de dos y tres variables.

El presente artículo está organizado de la siguiente forma: en §2 se explica el modelo en sus dos versiones y se efectúa el tratamiento analítico y numérico que conduce a la obtención de la curva de bifurcación y, respecto a esta, la clasificación de los puntos fijos en el espacio de parámetros. En §3 se exponen los aspectos experimentales y se muestra la concordancia de los resultados obtenidos con los predichos por el Oregonator; entre estos, la naturaleza homóloga entre un margen de bifurcación experimental con la curva de bifurcación teórica. En §4 se discuten tanto los resultados analíticos, numéricos y experimentales; haciendo énfasis en la pertinencia de cada uno de ellos y la relación entre estos. Finalmente, en §5 se dan las conclusiones y perspectivas de este trabajo.

2  Modelo y su análisis

2.1  Oregonator

[31994Gray & Scott] reportan el Oregonator con variables:

que intervienen en cinco etapas irreversibles:

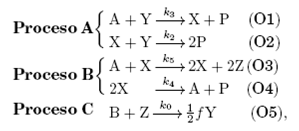
donde A=[BrO₃⁻], B=[CH₂(COOH)₂], k_i es la constante cinética asociada a la etapa i y k₀ corresponde a una etapa global; nótese además que (O3) constituye una etapa autocatalítica en X. Las ecuaciones cinéticas rescaladas resultantes constituyen un sistema de ecuaciones diferenciales no lineales autónomo:

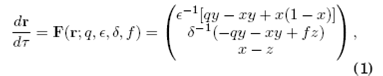
donde r(τ)=(x(τ), y(τ), z(τ))^T es un punto del espacio de fase Γ equivalente al espacio físico subtendido por X, Y y Z; además del coeficiente estequiométrico f, los parámetros de control son q, ϵ y δ definidos respecto a constantes cinéticas y/o concentraciones químicas:

Si la reacción BZ se lleva a cabo a pH=0. 097 ([H⁺]=0.8M), el valor de las constantes de velocidad de las etapas de los procesos inorgánicos del mecanismo FKN (k₂, k₃, k₄ y k₅) toman los siguientes valores según [31994Gray & Scott]

de modo que q=0.0008 y

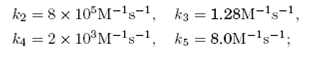
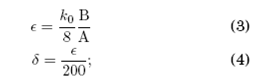
k₀ tiene carácter numérico y, del mismo modo que en [31994Gray & Scott] y [221995Mazzotti et al. Mazzotti, Morbidelli & Serravalle], se asigna por conveniencia el valor de 1 M⁻¹s⁻¹, por lo que el número de parámetros en las ecuaciones diferenciales (1) se reduce a dos: ϵ y f.

De la condición de velocidad de fase nula, 0=F(r_S;ϵ, f), se obtienen dos tipos de puntos fijos r_S:

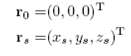
con

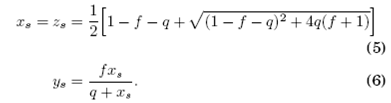
La estabilidad de un punto fijo es relativa a la dinámica de su perturbación, δr, que una vez linealizada se escribe

siendo L la matriz jacobiana de F(r;ϵ,f) evaluada en r_S, con soluciones δr=∑_i=1³c_ie^ω_i ^tu_i. Para el análisis cualitativo de estas trayectorias basta determinar el conjunto de valores propios {ω_i} que resulta de la ecuación característica

asociado al problema de valores propios [L(ϵ,f)−ωI]u=0, donde I es la matriz identidad.

Para determinar la naturaleza de los valores propios respecto a la estructura del polinomio característico en (8) serán útiles dos criterios expuestos en [62002Murray]:

Routh-Hurwitz. La condición necesaria y suficiente para que las tres raíces de (8) tengan parte real negativa es

Descartes. Si N es el número de cambios de signo en la secuencia de los coeficientes de (8) entonces habrá N o N−2 raíces reales y positivas.

2.1.1  Punto fijo r₀=(0,0,0)^T

El jacobiano de F evaluado en r₀ es

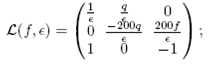
los coeficientes de su ecuación característica (8) están dados por:

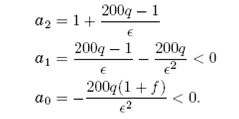
Teniendo en cuenta la regla de Descartes, cualquiera sea el signo de a₂ sólo habrá un cambio en la secuencia de los signos de los coeficientes del polinomio característico y, por tanto, el número de valores propios con parte real positiva será igual a uno, en consecuencia este punto fijo es siempre inestable.

2.1.2  Punto fijo r_s=(x_s,y_s,z_s)^T

La matriz del sistema linealizado correspondiente es

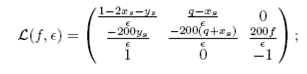
en este caso se encuentra que los coeficientes de la ecuación característica (8) son:

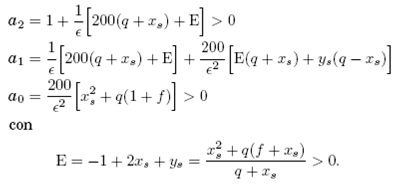
El signo de a₁ no está definido de modo que este determina la estabilidad de r_s. Si a₂a₁−a₀ > 0 entonces, de acuerdo al criterio de Routh-Hurwitz, la parte real de los valores propios será negativa y el punto fijo correspondiente será estable. Lo anterior implica que a₂a₁ > a₀ > 0 sí y solo sí a₁ > 0 y en consecuencia no hay cambio en los signos de los coeficientes del polinomio característico, por lo que, de acuerdo a la regla de Descartes, el número de valores propios con parte real positiva es nulo. La regla de Descartes permite también afirmar que los puntos fijos serán inestables si y solo si a₁ < 0, pues en tal caso hay dos cambios en el signo de los coeficientes del polinomio característico y, por tanto, el número de valores propios con parte real positiva será también dos. En este caso se verifica estrictamente que a₂a₁−a₀ < 0.

Los casos anteriores están separados por una bifurcación de Hopf donde la parte real de sus valores propios imaginarios son nulos, es decir, ω_2,3=±iΩ_c, siendo Ω_c=Im(ω_i) ≠ 0. Una vez reemplazadas las soluciones imaginarias en (8) se demuestra que la condición de bifurcación de Hopf para un sistema de tres variables es:

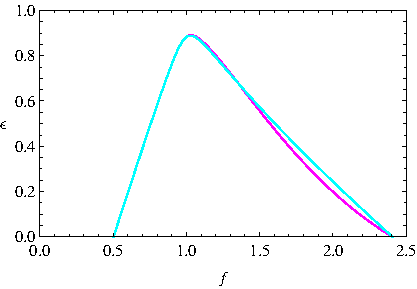
Figure 1: (Color online) Curva de bifurcación del Oregonator (magenta) y del Oregonator de dos variables (cian), descritos por (1) y (15) respectivamente.

De acuerdo a lo anterior, los puntos fijos r_s se pueden clasificar según:

Dado que ω_i=ω_i(q, f, ϵ), la estabilidad de un punto fijo puede representarse en el espacio de parámetros ϵ-f, para lo que basta analizar la condición de bifurcación de Hopf. Así, sustituyendo a₂, a₁ y a₀ en (10) se obtiene

donde ϵ_c indica el valor crítico de ese parámetro y

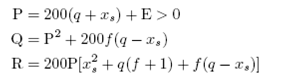
y dado que ϵ_c > 0, sólo es permitida la raíz positiva de la ecuación (11):

P, Q y R dependen de f y, estando q bien definido, sólo resta determinar el intervalo de variación de f para la función ϵ_c; para esto, considerando el caso límite ϵ_c=0 en (12) se obtiene [(R)/(P)]=0 y por tanto R=0, cuyas raíces constituyen las cotas inferior y superior del dominio de ϵ_c:

Dado que el número de intersecciones de la curva de bifurcación con el eje f es dos, cualquier valor fuera del intervalo (13) da un ϵ negativo, no permitido físicamente. En la Figura 1 se grafica la función ϵ_c=ϵ_c(q, f) en el espacio de parámetros ϵ-f con q=0.0008, cuyo análisis de puntos críticos da el máximo en (f^*, ϵ_c^*)=(1.0317, 0.89084) de acuerdo al criterio de la segunda derivada ([(d²ϵ_c)/(df²)]|_(f^*_=1.0317)=−13.4).

El cálculo de los valores propios de la ecuación característica (8) equivalen a las raíces del polinomio de tercer grado:

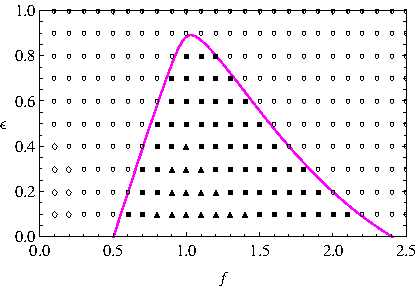
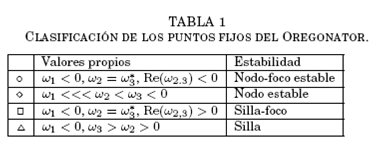
Figure 2: (Color online.) Clasificación de los puntos (f, ϵ) de acuerdo al criterio de Routh-Hurmitz y por la naturaleza de sus valores propios asociados de acuerdo a la Tabla 1. Los puntos en negro pertenecen a la región de inestabilidad (a₂a₁−a₀ < 0) y en blanco aquellos que son estables (a₂a₁−a₀ > 0). El límite de bifurcación de Hopf corresponde a a₂a₁−a₀=0.

de tercer grado:

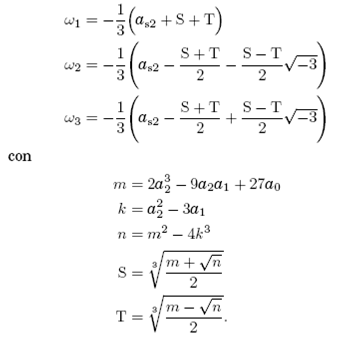
El cálculo de ω₁, ω₂ y ω₃ y la determinación del signo de a₂a₁−a₀ permite clasificar los puntos (f, ϵ) de acuerdo a su estabilidad tal como se muestra en la Figura 2 y en la Tabla 1 en la que se hace referencia a las etiquetas de cada región de acuerdo a la naturaleza de la parte real de los valores propios asociados.

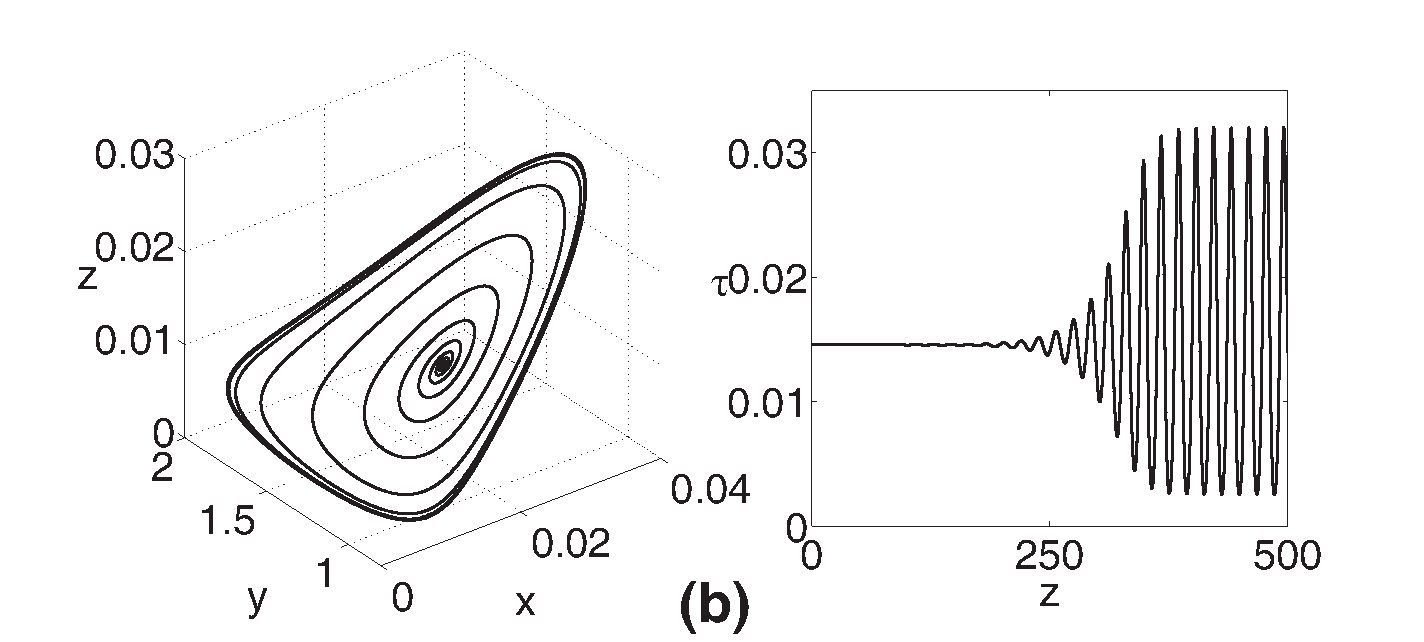
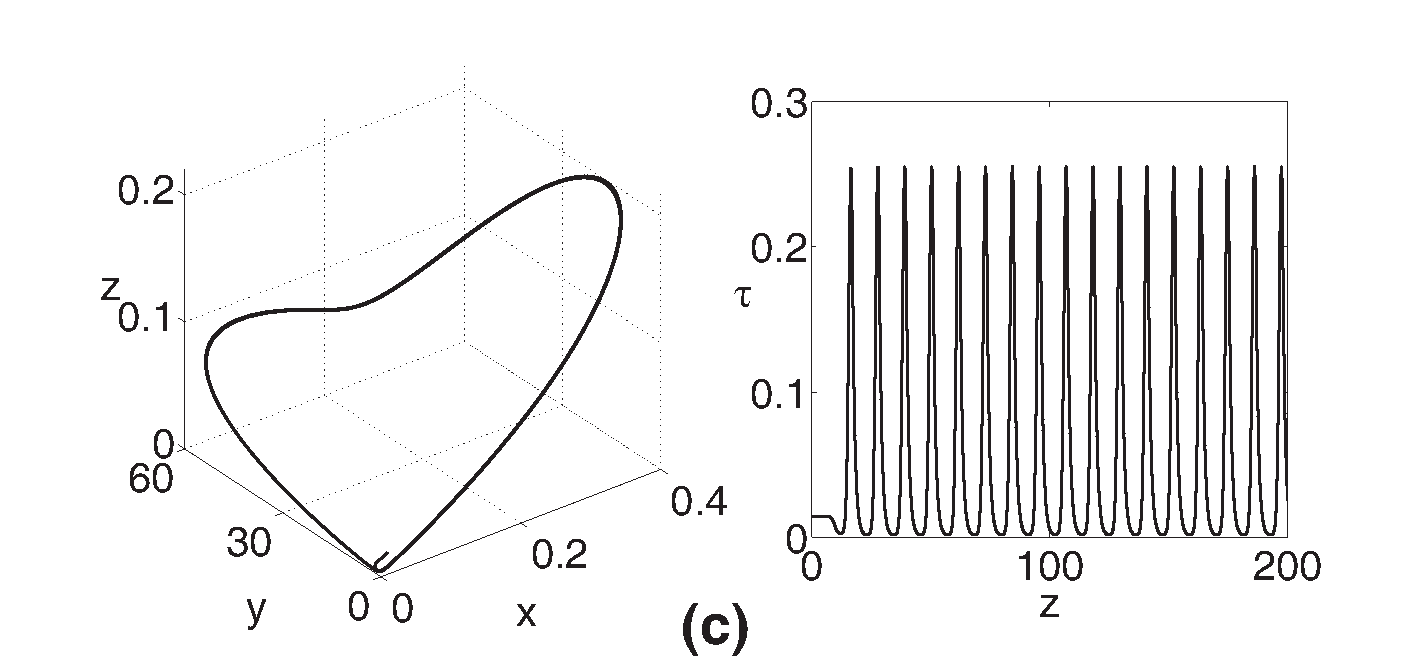
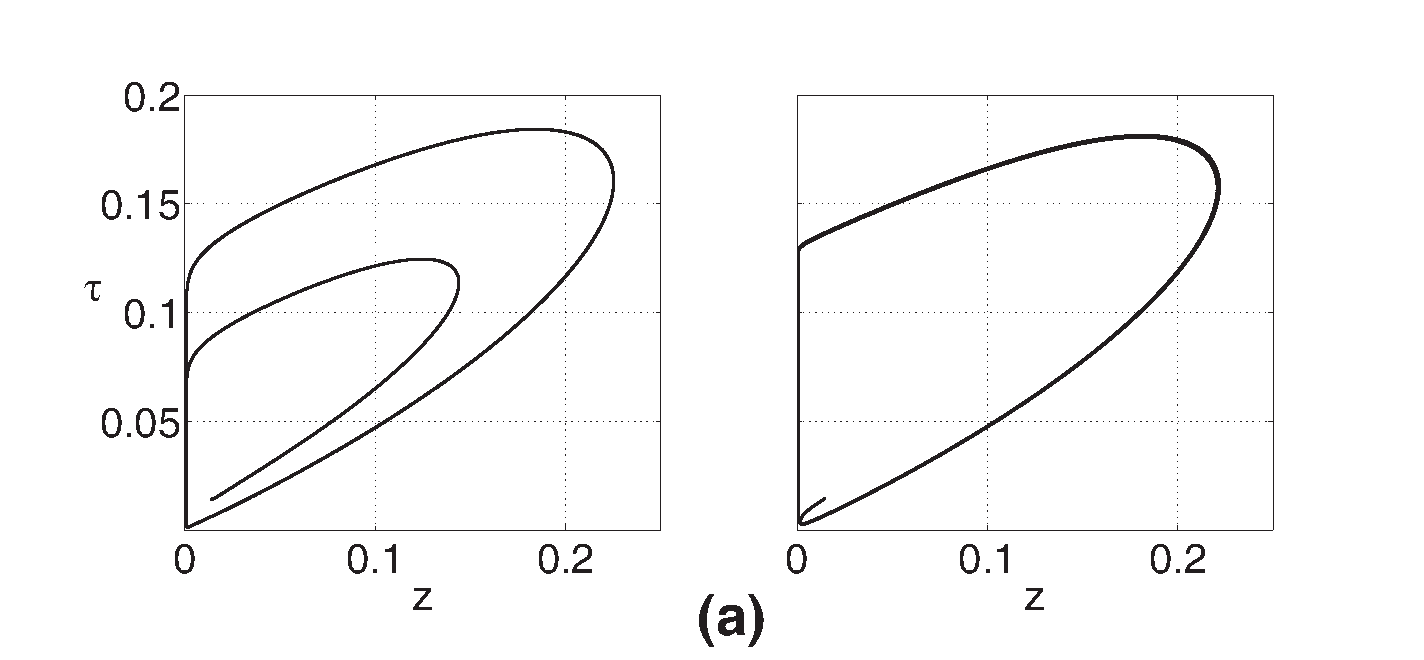
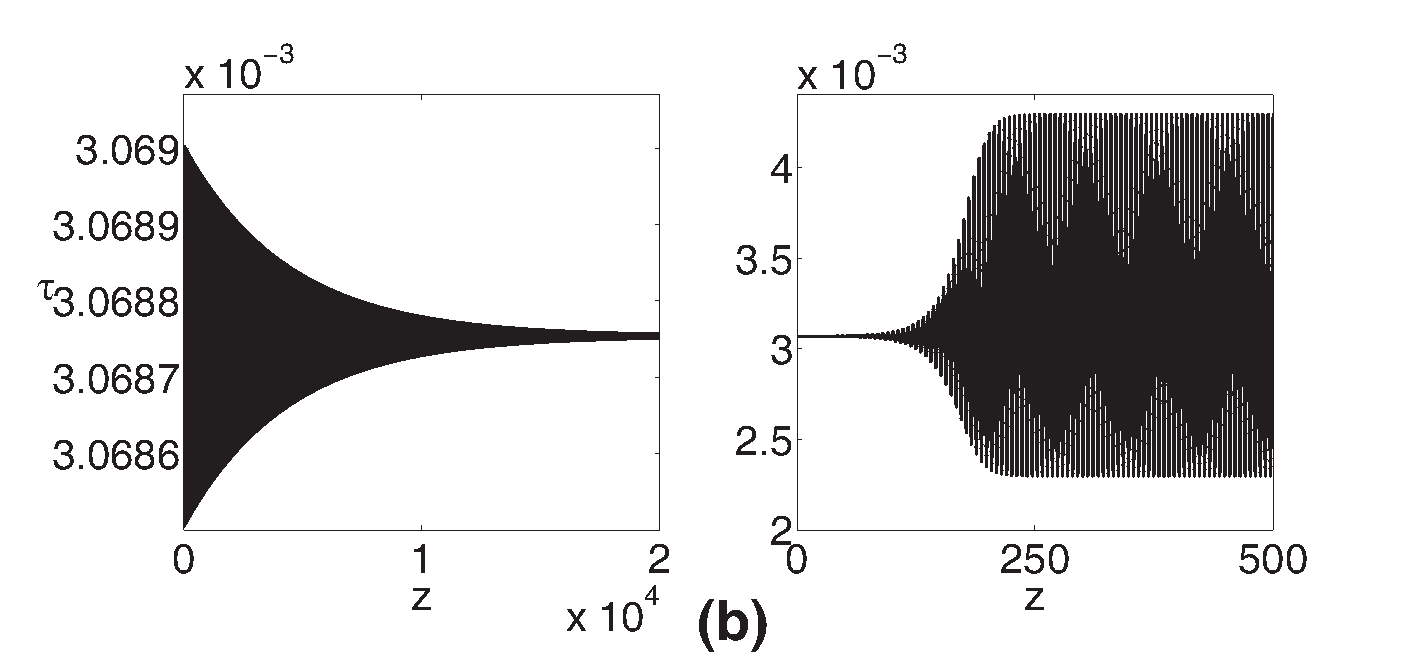
Se verificó la clasificación de los puntos fijos predicho por el análisis de estabilidad lineal llevando a cabo la integración numérica del Oregonator a través del método Runge-Kutta de cuarto orden asignándose una tolerancia relativa de 10⁻¹² y una tolerancia absoluta de 10⁻¹² en cada variable, el paso de integración fue 0.1 y las condiciones iniciales se definieron a partir de los puntos fijos truncados en la sexta cifra decimal con el fin de tener a estos, prácticamente, como referencia de la dinámica generada por su variación. De este modo, se obtuvieron las trayectorias en el espacio de fases y las series temporales correspondientes a puntos en el espacio de parámetros próximos a la región entre regímenes dinámicos distintos. En la Figura 3 se muestran los casos con f=1.1 y f=0.1 para diferentes valores de ϵ. Además, cada uno de estos se acompaña con los valores propios obtenidos del análisis de estabilidad lineal.

Figure 3: Espacio de fase (izquierda) y series temporales (derecha) para el Oregonator con q=0.0008. f=1.1 en los casos (a). nodo-foco estable, ϵ = 0.9 (ω₁=-4.4673, ω_2,3=-0.0132±0.3231i), (b), silla-foco, ϵ = 0.8 (ω₁=-4.9961, ω_2,3=0.0328±0.3424i) y (c). silla, ϵ = 0.3 (ω₁=-12.9681, ω₂=0.2655, ω₃=1.2213). f=0.1 para (d). nodo estable, ϵ = 0.3 (ω₁=-600.9862, ω₂=-2.4341, ω₃=-1.2323).

2.2  Oregonator de dos variables

Para fines de comparación se obtiene el límite de bifurcación en la versión de dos variables del Oregonator, a la que en adelante se denominará Oregonator 2D. La suposición fundamental es que, dado que el parámetro δ = ϵ/200 es particularmente pequeño, la velocidad de variación dy/dt se ajusta rápidamente a la composición instantánea de la mezcla pudiendo efectuarse la aproximación del estado estacionario dy/dt=0 (véase [31994Gray & Scott]; [231984Crowley & Field]), con lo que se obtiene

de este modo, el número de variables se reduce a dos, r=(x,z)^T, y el sistema de ecuaciones diferenciales queda en la forma:

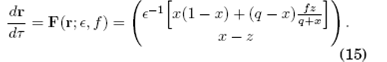
En este caso los puntos fijos son:

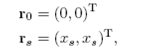
con x_s dado por (5).

La ecuación característica asociada al problema de valores propios tiene la forma:

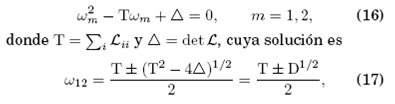
de modo que el discriminante D condiciona la naturaleza real o compleja de los valores propios mientras que T determina la estabilidad del punto fijo. Se debe mencionar que en esta caso, no es posible que se generen oscilaciones caóticas.

2.2.1  Punto fijo r₀=(0,0)^T

En este caso la matriz L del problema linealizado es

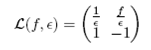
y la ecuación característica (16) tiene traza y determinante:

Por tanto, cualquiera sea el signo de T se tendrá siempre un cambio en el signo de los términos del polinomio característico; por lo que de acuerdo a la regla de Descartes, el número de raíces con parte real positiva será también uno. En consecuencia el punto fijo es inestable.

En estas circunstancias, D > 0 y el único caso límite posible es entre puntos silla cuando T=0, igualdad que implica la función constante ϵ = 1 cuyo intervalo de variación se obtiene de \triangle < 0, de donde f > −1, desigualdad válida siempre que f > 0. Por tanto, el punto fijo r₀ es inestable e inaccesible.

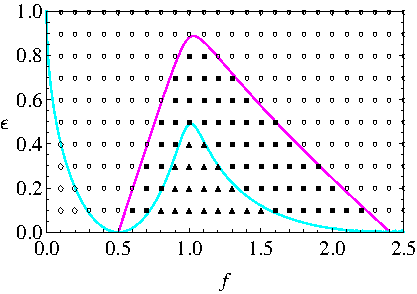
Figure 4: (Color online) Clasificación de los puntos (f, ϵ) para el Oregonator 2D de acuerdo al signo de la traza y por la naturaleza de sus valores propios asociados según la Tabla 2. Los puntos en negro pertenecen a la región de inestabilidad (T > 0) y en blanco aquellos que son estables (T < 0); además, en magenta, el límite de bifurcación de Hopf (T=0) y, en cian, el límite entre nodos y focos de igual estabilidad (D=0).

2.2.2  Punto fijo r_s=(x_s,x_s)

La matriz L del sistema linealizado es

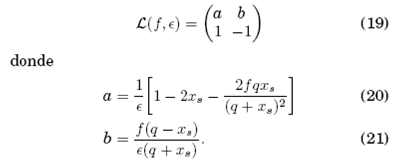
Las soluciones (17) de la ecuación característica (16) asociada están dadas en términos de la traza, T, y el determinante, \triangle, de L:

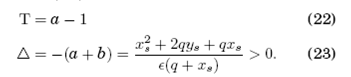
Dado que \triangle > 0, la condición de bifurcación de Hopf es T=0, a partir del cual se halla que

ecuación que define la región de bifurcación entre focos estables e inestables para el Oregonator 2D y que se muestra en la Figura 1 para q=0.0008. El dominio de la función ϵ_c=ϵ_c(f) es el mismo que el obtenido para el Oregonator, desigualdad (13), mientras que los valores máximos son (f^*, ϵ_c^*)=(1.0282, 0.8884); en este caso, el análisis de puntos críticos da [(d²ϵ_c)/(df²)]|_(f^*_=1.0282)=−14.6.

Se verificaron las regiones predichas por el límite de bifurcación del Oregonator 2D mediante la obtención de los valores propios (17) para diferentes intervalos de f y ϵ, clasificándose así los puntos fijos en el espacio de parámetros ϵ-f de la Figura 4 de acuerdo al discriminante y la traza tal como se indica en la Tabla 2.

Table 2: Clasificación de los puntos fijos del Oregonator de dos variables.

Para el Oregonator y el Oregonator 2D, tanto en la región de estabilidad y como en la de inestabilidad del espacio de parámetros se diferencian subregiones caracterizadas, en uno u otro caso, por valores propios reales o imaginarios. Para el Oregonator 2D el límite entre estos regímenes se obtiene de la condición D=0 cuya curva en el espacio de parámetros se muestra en la Figura 4.

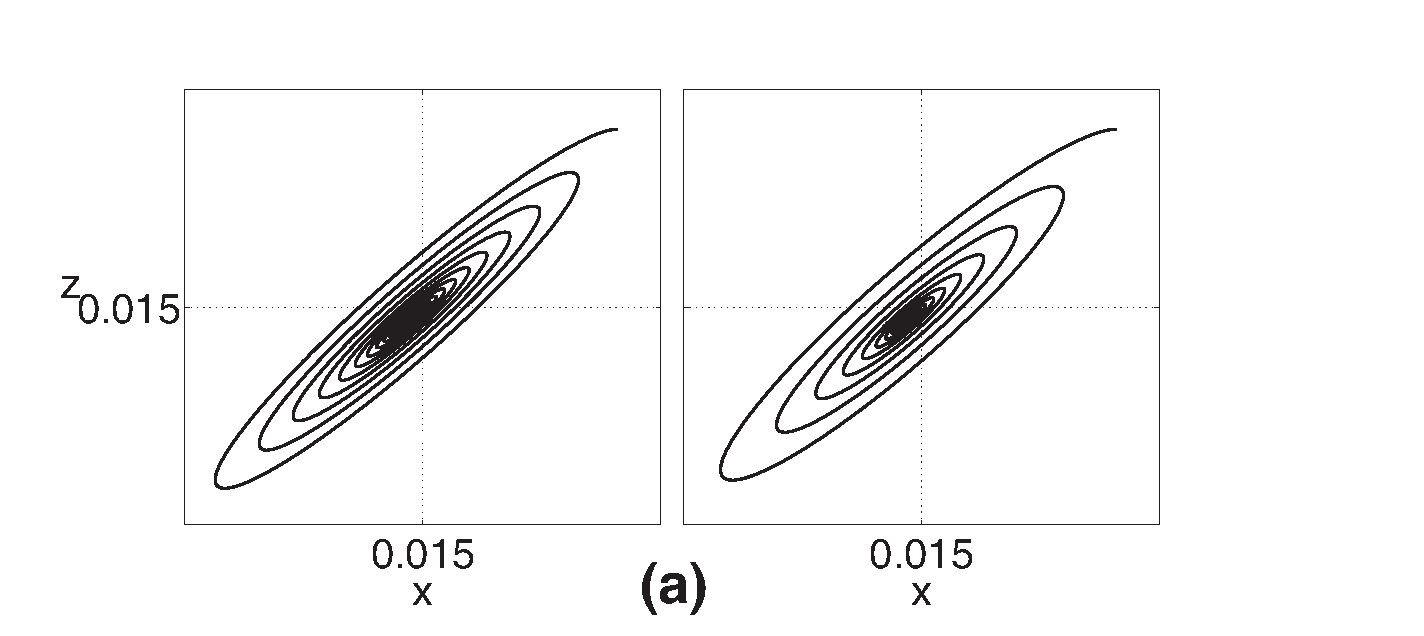
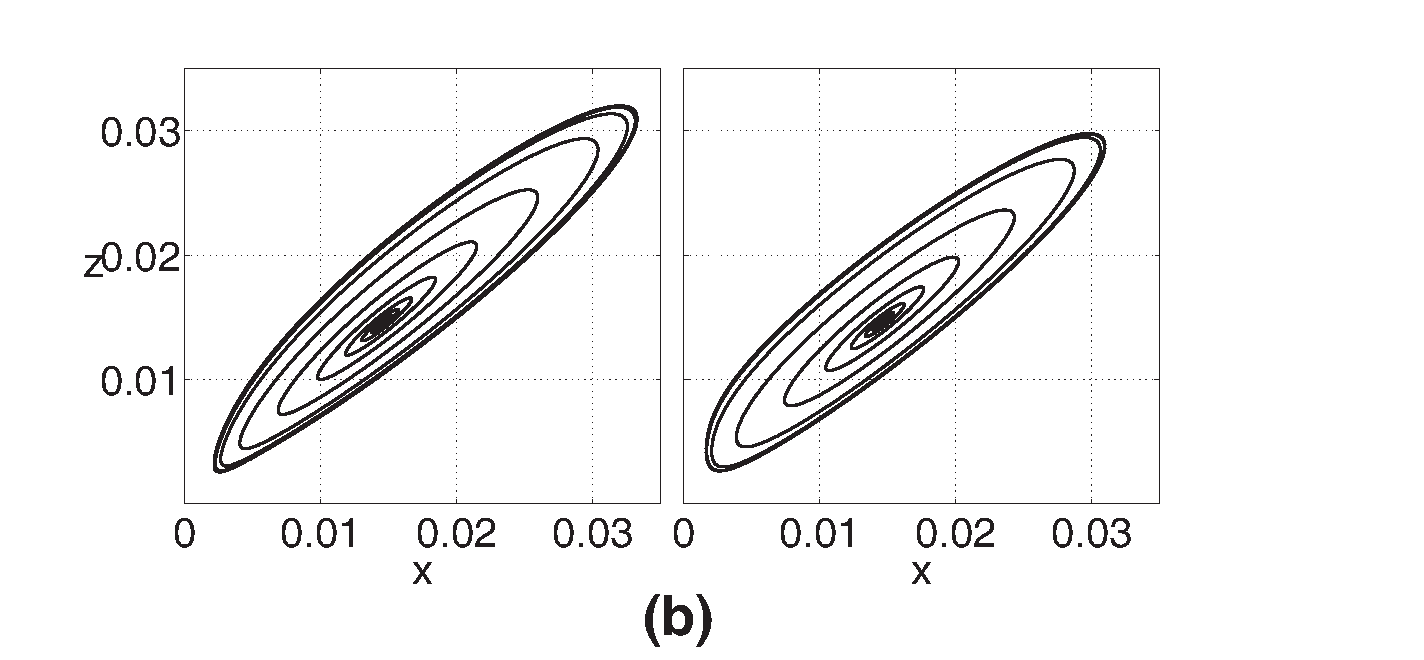
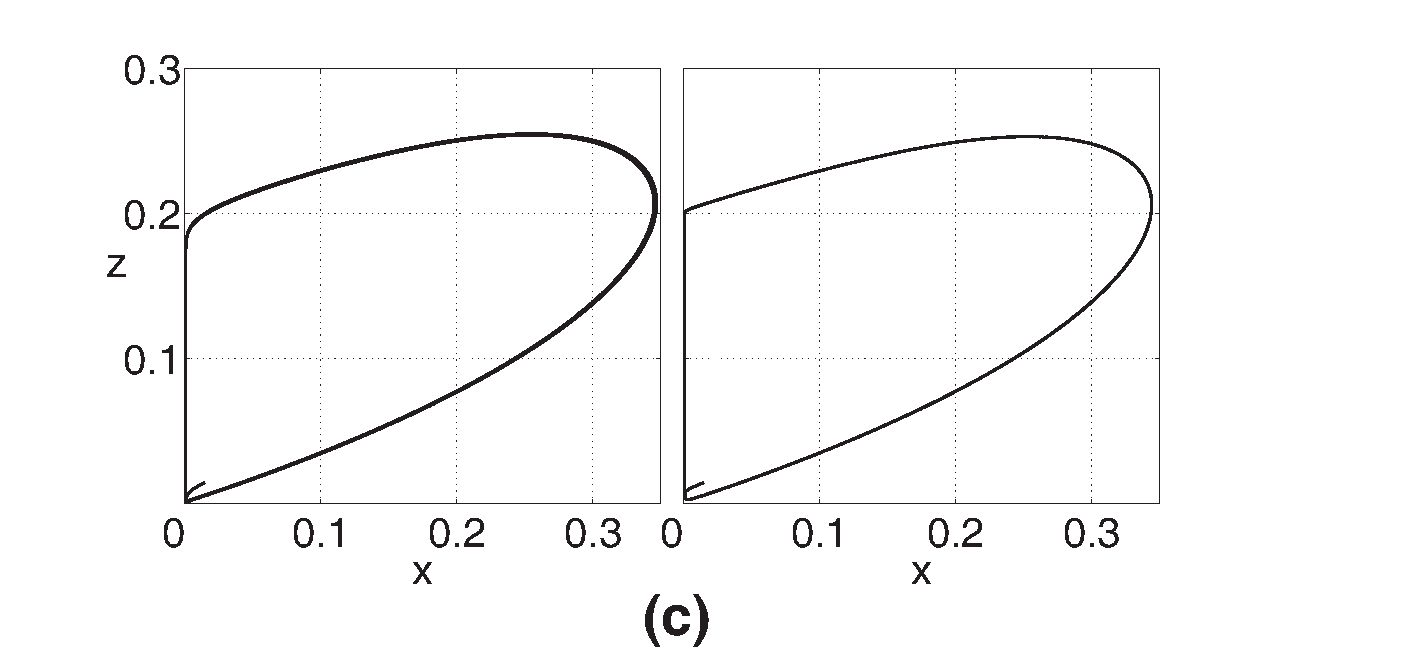
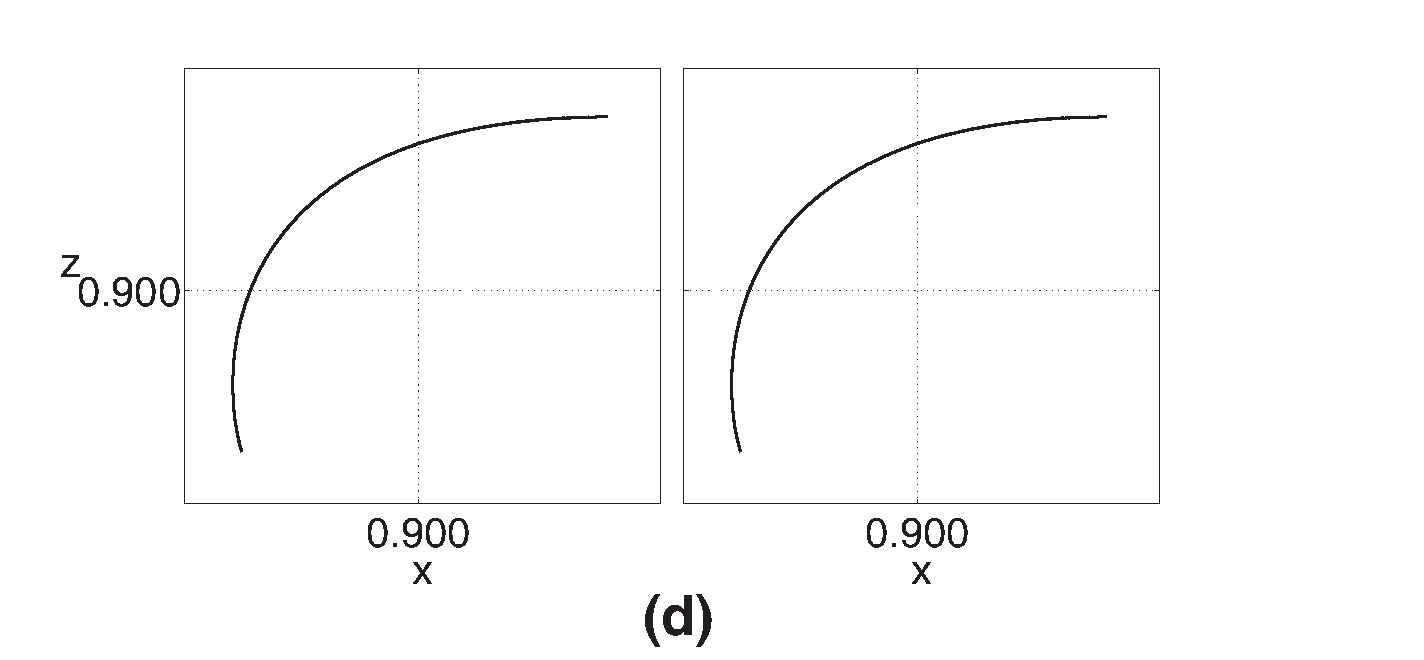
Por otro lado, mediante integración numérica de (15) se verifica la dinámica de los puntos que delimitan las diferentes regiones en la Figura 4, asignando las mismas condiciones de integración que se emplearon para el Oregonator. En la Figura 5 se compara la proyección de las trayectorias del Oregonator en el plano de fase z-x con las obtenidas a partir de su versión en dos variables, estos son casos que corresponden a puntos fijos cuyas etiquetas coinciden una vez sobrepuestos los espacios paramétricos de ambos modelos. En la Figura 6 se tienen ejemplos de casos en los que dichas etiquetas no coinciden, presentándose comportamientos menos concordantes: en 6-(a) se comparan un silla-foco (^[¯]) del Oregonator con un nodo inestable (\bigtriangleup) del Oregonator 2D, respectivamente; pero las situaciones realmente dispares son aquellas en los que las dinámicas son cualitativamente distintas, así por ejemplo, el caso 6-(b) corresponde a un nodo-foco estable (°) del Oregonator y un foco inestable (^[¯]) del Oregonator, respectivamente.

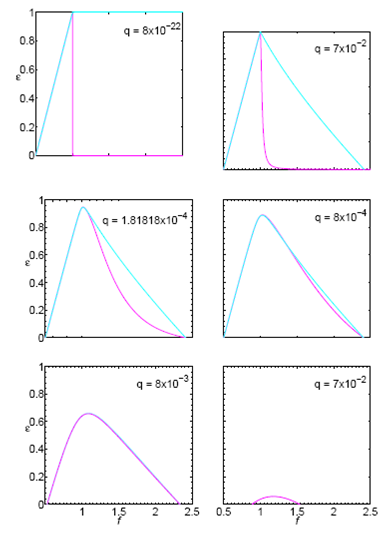
Las etiquetas para puntos fijos estables en el Oregonator pero inestables en el Oregonator 2D corresponden a la franja definida entre sus curvas de bifurcación mostrada en la Figura 1, la cual refleja la discrepancia entre ambos modelos. Dado que el perfil de bifurcación depende de los parámetros q y f (ver (12) y (24)) lo mismo ocurre con la región de discrepancia tal como se observa en la Figura 7.

3  Aspectos experimentales

3.1  Modelo FKN ampliado

Los valores de los parámetros f y k₀ que aparecen en el Oregonator tienen un carácter numérico debido a la falta de información cinética de las etapas orgánicas de la reacción BZ en la época que dicho modelo fue propuesto. Hoy se entiende mejor estos procesos y se reconoce el rol dinámico de especies como el ácido bromomalónico (BrAM), derivado del ácido malónico (AM).

Considérese la versión ampliada del mecanismo FKN en el que el ión Ce⁺⁴ oxida tanto a AM como a BrAM, según se expone en [31994Gray & Scott]:

Figure 5: Plano de fase z-x (derecha) para la versión reducida del Oregonator, q=0.0008. f=1.1 en los casos: (a). foco inestable, ϵ = 0.9 (D=−0.5456, T=−0.0419, ω_1,2=−0.0209±0.3693i), (b). foco estable, ϵ = 0.8 (D=−0.6097, T=0.0778, ω_1,2=0.0389±0.3904i) y (c) punto silla, ϵ = 0.3 (D=1.8707, T=1.8742, ω₁=1.6210,ω₂=0.2532). Para f=0.1: (d). nodo estable, ϵ = 0.3 (D=1.4527, T=-3.6684, ω₁=-1.2316, ω₂=-2.4369). A la izquierda, los planos de fase z-x correspondientes al Oregonator de tres variables.

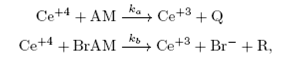
cuyas ecuaciones cinéticas son, respectivamente,

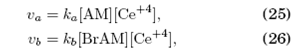
y Q y R son productos inertes. La combinación de ambas etapas da la reacción neta:

Figure 6: Comparación la dinámica de un punto fijo con diferentes etiquetas en el espacio de parámetros del Oregonator (izquierda) con el correspondiente al del Oregonator 2D (derecha). q=0.0008, ϵ = 0.4. (a) f=1.1, Oregonator: ω₁=−9.7755, ω₂₃=0.4572±0.1813i; Oregonator 2D: ω₁=0.7391, ω₂=0.4166. (b) f=1.7, Oregonator: ω₁=-3.8204, ω₂₃=−0.0002±0.8425i; Oregonator 2D: ω₁₂=0.0452±1.1831i, en este último caso se vio conveniente emplear las series temporales de la variable z en vez del plano de fase z-x.

cuya ley de velocidad empírica es

A partir de (25), (26) y (28) se demuestra que:

con

Para un pH = 0.097, las ecuaciones (3) y (29) indican que los valores de ϵ y f pueden modificarse variando las concentraciones de reactivos respecto a los cuales están definidos, lo que, en principio, plantea la obtención experimental del espacio ϵ-f una vez que se asocia a cada punto (f, ϵ) la variación temporal, esto es, la serie cinética de alguna de las concentraciones relacionadas a las variables dinámicas del Oregonator.

3.2  Reacción de Belousov-Zhabotinsky en reactor cerrado y espacio de concentraciones.

El Oregonator modela un régimen estacionario de la concentración de reactivos e intermedios en un reactor agitado de flujo contínuo de sustancia. Experimentalmente se tuvo la posibilidad de llevar a cabo la reacción BZ en reactor cerrado, observándose oscilaciones durante horas y su tendencia al equilibrio (ver [42004Oporto Almaraz & Ramírez Ávila]). Por tanto, puede suponerse que la dinámica en un sistema de flujo contínuo significa un instante del proceso que se lleva a cabo en reactor cerrado; experimentalmente dicho instante puede aproximarse a un intervalo de tiempo finito, mayor o menor, siempre que mantenga determinado grado de correspondencia con el sistema de flujo contínuo, de modo que el valor de las concentraciones iniciales de AM, BrAM y BrO₃⁻ permitirían obtener experimentalmente los puntos del espacio de parámetros ϵ-f.

En la práctica, el planteamiento expuesto requiere consideraciones adicionales. Los puntos (f, ϵ) no están completamente definidos a partir de las ecuaciones (3) y (29) debido a que no se conoce los valores de las constantes k_a y k_b; rescribamos dichas ecuaciones del siguiente modo:

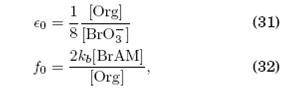
donde f₀=fk₀ y ϵ₀=ϵ/k₀ con unidades M⁻¹s⁻¹ y Ms, respectivamente, y de acuerdo a (27)

un instante antes de que comience la reacción. El espacio ϵ₀-f₀ se denominará espacio de concentraciones, equivalente a ϵ-f. La constante k_b juega un rol de factor de escala en la ecuación de f₀ al que se le asigna un valor de k_b = 0.5M⁻¹s⁻¹, mientras que ϵ₀ queda completamente definido respecto a las concentraciones de las especies orgánicas y del ión bromato.

3.3  Concentraciones de referencia y procedimiento.

El número de variables en (31), (32) y (33) puede disminuirse a [AM] y [BrO₃⁻] manteniendo el valor de [BrAM] constante, lo que es posible llevando a cabo la reacción de bromación con una pequeña cantidad de bromuro como reactivo limitante:

una vez que se lleva a cabo esta reacción se definen las concentraciones molares de referencia:

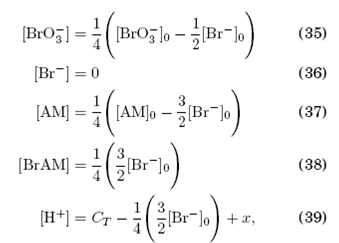
donde la concentración formal total de H₂SO₄, C_T, está dada por

y, empleando la teoría de los equilibrios ácido-base para la disociación de H₂SO₄, se demuestra que

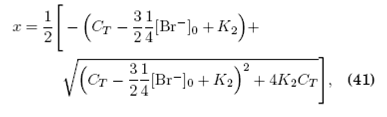
siendo K₂=10^−1.92 la constante ácido-base para la segunda disociación del H₂SO₄. El significado de C₁₀ y C₂₀ se expone a continuación.

En las ecuaciones (35) a (41), 1/4 es un factor de corrección por dilución respecto a las concentraciones iniciales formales [P]₀, donde P representa la fórmula molecular de los reactivos, debido a que la reacción de bromación se lleva a cabo mezclando tres soluciones, cada una de volumen V_T/4, con concentraciones [AM]₀/[Br⁻]₀, [BrO₃⁻]₀ y C₂₀=[H₂SO₄]₂₀, mezcla que se agita y a la que a continuación se añade un volumen V_T/4 de una solución [Ce(III)]₀/C₁₀ dando así inicio a la reacción BZ. El volumen total de la mezcla es V_T=0.9 ml. el cual se agita y se traspasa a una cubeta de cuarzo que introducida en un equipo UV-visible (Lambda-25) permite obtener la serie temporal de la absorbancia de la reacción a una longitud de onda de 400 nm.

A partir de (35), (37) y (38) se determinan los puntos (f₀, ϵ₀) mientras que la concentración de ión hidronio en (39) permite calcular el pH de la solución.

Las concentraciones formales (F) iniciales de las soluciones de reactivos fueron:

[AM]₀/[Br⁻]₀=[AM]₀ F/0.0100 F, para diferentes [AM]₀.

[BrO₃]₀, en diferentes concentraciones.

C₂₀=[H₂SO₄]₂₀=1.3447 F para pH = 0.097.

C₂₀=[H₂SO₄]₂₀=0.1506 F para pH = 0.3.

[Ce(III)]₀/C₁₀=0.0080 F/1.8231 F.

La preparación de las soluciones mencionadas se hizo por pesada de sustancias sólidas: CH₂(COOH)₂ al 98%, Ce₂(SO₄)₃ al 97% y KBrO₃ y NaBr, ambos, químicamente puros. La única sustancia líquida empleada fue el H₂SO₄ 18.2310 F, concentración obtenida por titulación con una solución de NaOH 0.1375 F a la vez valorada con una solución de HCl 0.1141 F, concentración que se determinó por pesada directa de Na₂CO₃ químicamente puro.

3.4  Resultados.

Los puntos en el espacio de concentraciones ϵ₀-f₀ se clasifican en dos regiones: una de estados estacionarios y otra de oscilaciones; en ambos casos, con presencia de un transiente corto. Algunos de dichos puntos se muestran en la Figura 8. Mediante un examen visual se identificaron oscilaciones periódicas como el punto (0.037,1.58), biperiódicas como (0.037,0.56), irregulares como (0.037,0.42) e histéresis entre regímenes oscilantes, (0.015,1.40), o entre un estado estacionario y uno oscilatorio, (0.012,1.58); casos de este último tipo pueden corresponder a oscilaciones precedidas por periodo de inducción. Dado que el fenómeno de histéresis refleja las variaciones temporales de los parámetros de control así como de la concentración de ión hidronio, una serie cinética que presenta periodo de inducción no puede realmente asociarse a un punto (f₀, ϵ₀); razón por la cual estos casos se excluyen de la región de oscilación.

Se define como el margen de bifurcación a la región comprendida entre los puntos máximos de oscilación

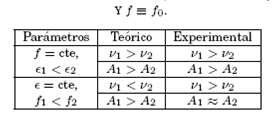
Table 3: Comparación de la variación de la amplitud (A) y la frecuencia (ν) respecto a los parámetros de control entre las oscilaciones obtenidas teóricamente y el comportamiento experimental, asumiéndose que ϵ ≡

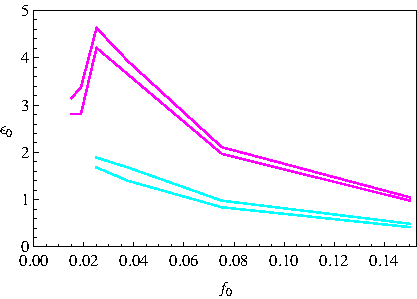
y los puntos mínimos de los estados estacionarios en el espacio ǫ0–f0, que unidos por una línea dan una idea del límite de bifurcación experimental. Con base en los datos experimentales, en la Figura 9 se compara el margen de bifurcación a pH 0.097 y 0.3.

En la Tabla 3 se resume el comportamiento de los ritmos de oscilación experimentales (véase Figura 8) y se los compara con los diferentes casos predichos por el Oregonator tanto a f como para ǫ constantes,

 

4  Discusión

El espacio de parámetros constituye el ámbito de existencia del sistema en el sentido de que representa las posibilidades dinámicas a las que este puede acceder. Por esta razón, el resultado más importante del tratamiento analítico y numérico de las ecuaciones diferenciales del Oregonator es la clasificación de sus puntos fijos en el espacio de parámetros ϵ-f de acuerdo a su estabilidad y la obtención de la curva de bifurcación. De forma análoga para los resultados experimentales, la obtención de los puntos del espacio de concentraciones ϵ₀-f₀ y el margen de bifurcación.

Analíticamente se obtuvieron dos tipos de puntos fijos: r₀ y r_s. Debido a la nulidad en las variables dinámicas, el primer caso constituye un punto fijo que no da lugar a la reacción y que es inestable respecto a las variedades invariantes asociadas a r_s. El análisis llevado a cabo con algún detalle para el Oregonator 2D demostró que r₀=(0, 0) es un punto silla que, en consecuencia, es inaccesible cualquiera sea el valor de ϵ y f; o desde el punto de vista químico, cualesquiera sean las concentraciones que definen estos parámetros. Lo último se debe a que dichas concentraciones no llegan a mezclarse de modo que den lugar a la reacción BZ.

Experimentalmente se comprobó que la ocurrencia de la reacción BZ constituye una perturbación de un sistema no reactivo, que puede asociarse al punto fijo r₀, una vez que se mezclan dos soluciones cuyas concentraciones (dadas en un caso por las Ecuaciones (35) a (38) y en el otro por [Ce(III)]) constituyen magnitudes instantáneas que varían desde el comienzo de la reacción y a partir de las cuales se calculan los puntos (f₀, ϵ₀). De hecho, gran parte de las series cinéticas, oscilantes o no, presentan un transiente que da una idea del carácter perturbativo de la ocurrencia de la reacción.

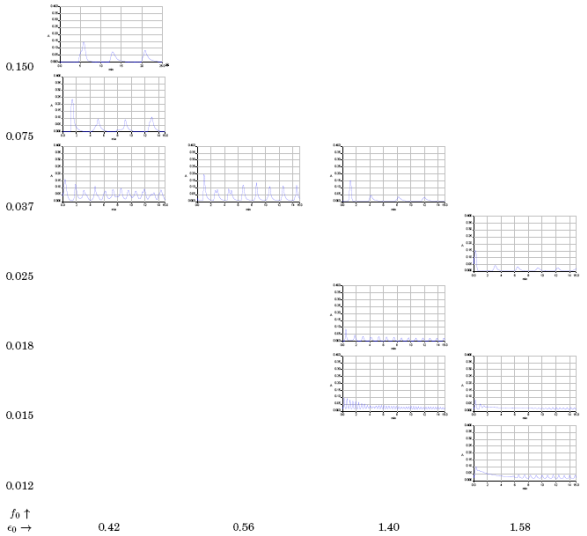
Figure 8: Ritmos de oscilación a diferentes valores de ϵ₀ medidos a un tiempo de 15 minutos, el caso indicado con asterisco corresponde a 25 minutos.

Figure 9: (Color online) Margen de bifurcación en el espacio de concentraciones ϵ₀-f₀ a pH = 0.097 (magenta) y pH = 0.300 (cian); nótese la similaridad en forma entre estas curvas experimentales y las teóricas (ver Figura 1).

La clasificación de los puntos fijos r_s en el espacio de parámetros ϵ-f para el Oregonator y el Oregonator 2D es cualitativamente la misma: una región de estabilidad, otra de inestabilidad y, como límite entre estas, la curva de bifurcación de Hopf, ϵ_c=ϵ_c(f, q). Aunque el dominio en ambos casos es prácticamente el mismo su discrepancia está dada por la franja entre sus curvas de bifurcación (ver Figura 1).

La curva de bifurcación mostrada en la Figura 1 para el Oregonator tiene la misma forma que la reportada por [221995Mazzotti et al. Mazzotti, Morbidelli & Serravalle] bajo las mismas restricciones ([H⁺]=0.8 M, q=0.0008 y k₅=1M⁻¹s⁻¹, este último equivalente al empleado k₀) pero con un rescalamiento tal que los parámetros de bifurcación son f y el cociente b/a (equivalente a ϵ), siendo a=A/A₀ y b=B/B₀ las concentraciones adimensionales de los reactivos con A₀=B₀=1 M. Si bien el dominio de las curvas de bifurcación es el mismo en ambos casos, estas difieren; por ejemplo a partir del cociente entre sus valores máximos, [((b/a)_c^*)/(ϵ_c^*)], se tiene que: ϵ_c^* ≈ [1/8.3]([(b)/(a)])_c^*.

Pero, principalmente, los resultados teóricos se corroboraron experimentalmente pues el espacio de concentraciones ϵ₀-f₀ obtenido a pH 0.097 presenta la misma tendencia de distribución que la predicha por el Oregonator, esto es, una región de oscilación y otra de estados estacionarios separadas ambas por un margen de bifurcación (Figura 9), este último, similar a la curva de bifurcación en el espacio ϵ-f (Figura 1). Dejando de lado los factores de escala introducidos a través de los parámetros del Oregonator y del mecanismo FKN ampliado, el espacio de concentraciones es relativo al cociente [Org]/[BrO₃] (en las ordenadas) y a la cantidad [Org]/[BrAM] (en las abscisas) de modo que la semejanza entre la curva de bifurcación teórica y el margen de bifurcación es en realidad una semejanza del modelo y los resultados experimentales; aspecto este de importancia pues basta determinar los cocientes indicados para el estudio cualitativo del espacio de concentraciones.

Otro aspecto importante del tratamiento analítico y numérico del Oregonator es la dependencia paramétrica del perfil de bifurcación y de la franja de discrepancia respecto a q, tal como se aprecia en la Figura 7. La curva de bifurcación varía de modo tal que la franja de discrepancia disminuye conforme el valor de q aumenta tendiendo a hacerse prácticamente nula a medida que la reacción BZ se inhibe. Por otro lado, esta franja aumenta a medida que q disminuye llegando a hacerse infinita; mientras que en el caso del Oregonator las cotas del intervalo de f tienden a valores límite, f_a→ 0.5, f_b→ 1 y ϵ_c^*→ 1, de modo que su perfil de bifurcación se asemeja a un triángulo pues f_b→ f(ϵ^*_c). A pesar de que el Oregonator 2D presenta anomalías para valores muy pequeños de q, resulta aceptable para las regiones definidas entre la cota inferior del intervalo de f y el valor correspondiente al máximo de la curva de bifurcación, f^*(ϵ^*).

Desde el punto de vista químico, una vez fijado el pH, el valor de q también se fija, de modo que el perfil de bifurcación está condicionado por la acidez de la solución. Por ejemplo, en la Figura 7 los perfiles con q = 1.81818×10⁻⁴ y q = 8×10⁻⁴ corresponden a los valores de las constantes cinéticas, respectivamente, a [H⁺]=0.26 (según los datos reportados en [171991Györgyi et al. Györgyi, Rempe & Field]) y [H⁺]=0.8 (empleado en el presente trabajo). De acuerdo a lo anterior, el valor de q aumenta con [H⁺], de modo que el margen de bifurcación a pH = 0.3 presenta un corrimiento respecto al margen de bifurcación a pH = 0.097. Por otro lado, la disminución del margen de bifurcación al aumentar el pH podría deberse a la tendencia de la reacción a inhibirse conforme el medio disminuye su acidez, en este caso la variación de q sería de forma inversa a [H⁺].

Un aspecto de concordancia entre los resultados experimentales y el modelo está en que la tendencia de los ritmos de oscilación de diferentes casos obtenidos a f₀ fijo es la misma que los que se observan en las series temporales a f fijo, tal como se muestra en la Tabla 3; sin embargo, los ritmos de oscilación de los casos obtenidos a ϵ₀ fijo presentan una tendencia opuesta en la variación de la frecuencia respecto a los casos a ϵ fijo.

Por otro lado, las regiones predichas por la curva de bifurcación del Oregonator y del Oregonator 2D fueron corroboradas obteniéndose los valores propios que resultan de la correspondiente ecuación característica del sistema linealizado tal como se muestra en las Figuras 2 y 4. En la Tabla 4 se comparan ambos casos donde se evidencia que, a excepción de los puntos fijos tipo nodo estable, el modelo con tres variables contiene información adicional aunque el Oregonator 2D rescata los aspectos esenciales.

Table 4: Estabilidad de los puntos fijos para el Oregonator y su versión reducida de dos variables.

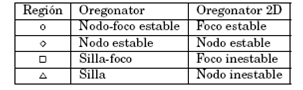
Así por ejemplo, una vecindad local de un punto silla no se diferencia de un nodo inestable perturbado y por tanto los puntos \bigtriangleup de ambos modelos son equivalentes; lo mismo ocurre con los puntos ° y ^[¯].

Los valores propios dan información sobre la naturaleza del punto fijo y la manera en que este responde a una perturbación; por tanto, en el caso de los puntos fijos estables se conoce además la variedad invariante a la que tiende el sistema perturbado aunque esto no ocurre con los puntos fijos inestables. Por ejemplo, el análisis de estabilidad de puntos fijos indica que \bigtriangleup es un punto silla pero no la variedad invariante respecto a la cual es inestable. Por esta razón la integración numérica del sistema de ecuaciones diferenciales complementa la información dada por el análisis de estabilidad lineal. La Figura 3 ilustra los resultados obtenidos para el Oregonator, de los cuales se apuntan las siguientes observaciones:

- Una perturbación de un punto fijo silla-foco, 3-(b), se amplifica de forma progresiva a través de una dinámica oscilante conforme los términos imaginarios de las soluciones toman relevancia respecto a los términos asintóticos.

- Los puntos tipo silla, 3-(c), se diferencian de los anteriores debido a que los términos asintóticos de sus soluciones se desvanecen rápidamente para dar lugar a la dinámica oscilante.

- Los nodo-foco estables, 3-(a), son el caso inverso de los silla-foco inestables, estos amortiguan gradualmente la perturbación a través de oscilaciones debido a la combinación de términos imaginarios y asintóticos en las soluciones.

- Un nodo-estable perturbado, 3-(d), se restituye solo mediante términos asintóticos.

Se concluye que todo punto fijo inestable r_s lo es respecto a un ciclo límite de periodo definido y todo punto fijo estable r_s lo es respecto a un estado estacionario, ya sea para el Oregonator o su versión 2D.

En los casos mencionados, las Figuras 5 y 6 comparan el subespacio de fase z-x para el Oregonator y el espacio z-x de su versión reducida, constatándose que las trayectorias del Oregonator 2D constituyen de forma aceptable una proyección del ciclo límite tridimensional en el espacio de fases bidimensional siempre que los puntos (f,ϵ) no se encuentren en la franja de discrepancia entre las curvas de bifurcación de Hopf, es decir, en aquellos casos en los que las etiquetas de los puntos fijos no coinciden una vez sobrepuestos el espacio de parámetros de ambos modelos.

5  Conclusiones y perspectivas

En reactor cerrado y a pH = 0.097 se obtuvieron las regiones de oscilación y estados estacionarios en el espacio de concentraciones ϵ₀-f₀ respecto al margen de bifurcación con una distribución homóloga al de las regiones de inestabilidad y estabilidad de los puntos fijos r_s respecto a la curva de bifurcación en el espacio de parámetros ϵ-f a q=0.0008 predichas por el Oregonator. También se evidenció experimentalmente que el margen de bifurcación disminuye a medida que el pH aumenta, comportamiento que presenta la curva de bifurcación cuando el valor del parámetro q aumenta. Un otro tipo de punto fijo corresponde al estado estacionario r₀ de naturaleza no reactiva en el sentido de que las especies químicas a partir de las cuales se lleva a cabo la reacción BZ no llegan a ponerse en contacto.

Por tanto, se considera al Oregonator como una aproximación cualitativa satisfactoria de la reacción BZ en reactor cerrado, o lo que es lo mismo, con flujo de sustancia nulo, dada la forma homóloga de la región de bifurcación en el espacio de parámetros con la que presenta el espacio de concentraciones. Estos resultados sugieren la comprobación de la existencia de regiones de estados estacionarios seguida de otra de periodo simple en los diagramas de bifurcación a velocidades de flujo nulo o muy bajo reportados, por ejemplo, en [171991Györgyi et al. Györgyi, Rempe & Field].

Por otro lado, el Oregonator 2D resulta suficiente para el análisis del Oregonator siempre que el valor de sus parámetros de control no signifiquen un punto (f, ϵ) en la región de discrepancia comprendida entre las curvas de bifurcación de ambos modelos, discrepancia que disminuye a medida que el valor de q aumenta a la vez que la reacción BZ se inhibe a pH elevado. Finalmente, el Oregonator 2D será siempre satisfactorio en la región comprendida entre el límite inferior del dominio de f y el valor de f^* correspondiente al punto máximo (f^*, ϵ_c^*).

Los aspectos mencionados son relevantes considerando que un modelo como el Oregonator de cinco etapas irreversibles puede reproducir las características más relevantes de la compleja reacción BZ y emplearse, dada su relativa simplicidad, para el análisis de fenómenos más complejos.

Desde el punto de vista experimental, se sugiere verificar los resultados obtenidos además de llevar a cabo pruebas a diferentes pH e investigar la acidez a la que la reacción BZ se inhibe. Estas pruebas requieren optimizar el procedimiento experimental, por ejemplo, variando la cantidad de Br⁻ que interviene en la reacción de bromación para así comprender su efecto sobre las series temporales, lo que requiere además cuantificar los ritmos de oscilación. Para dotar al Oregonator de un carácter cuantitativo se sugiere determinar las constantes de velocidad o los factores de escala a partir de los cuales se planteó el procedimiento experimental, de modo que el margen de bifurcación se ajuste lo mejor posible a la curva de bifurcación predicha por el Oregonator. También, debe orientarse la explicación de la riqueza dinámica observada en la reacción BZ con base en el Oregonator.

Desde el punto de vista analítico, el presente trabajo plantea obtener el diagrama de bifurcación de Hopf para el Oregonator, lo que en principio explicaría la transición de escenarios dinámicos de un régimen estacionario a uno oscilatorio. Mediante un análisis similar pero con base en modelos más completos de la reacción BZ, determinar si el Oregonator está presente en la región del diagrama de bifurcación respecto al flujo de sustancia correspondiente a oscilaciones simples. Se considera necesario un estudio más detallado del punto fijo r₀ y en el caso de r_s obtener una forma analítica del límite entre puntos fijos con valores propios reales de aquellos de naturaleza imaginaria. También se sugiere establecer alguna relación cuantitativa entre el pH de la solución y el perfil de bifurcación y la franja de discrepancia.

AGRADECIMIENTOS

Agradecemos la invaluable y desinteresada colaboración en la parte experimental, prestada por el personal del Laboratorio de Química de Alimentos de la Carrera de Ciencias Químicas de la UMSA, en especial al Dr. Mauricio Peñarrieta. También apreciamos las sugerencias hechas por el Referee que sirvieron para mejorar el presente trabajo.

References

[11972Field et al.Field, Körös, & Noyes]

1. Field R. J., Körös E. & Noyes R. M. (1972), J. Am. Chem. Soc. 94, 25, 8649.         [ Links ]

[22007Zhabotinsky ]

2. Zhabotinsky A. M. (2007), Scholarpedia 2, 9, 1435.         [ Links ]

[31994Gray & Scott]

3. Gray P. & Scott K. (1994), Chemical oscillations and instabilities (Oxford: Oxford University Press).         [ Links ]

[42004Oporto Almaraz & Ramírez Ávila]

4. Oporto Almaraz S. A. & Ramírez Ávila G. M. (2004), Revista Boliviana de Física 7, 45.         [ Links ]

[51994Goldbeter]

5. Goldbeter A. (1994), Biochemical oscillations and cellular rhythms (Cambridge: Camridge University Press).         [ Links ]

[62002Murray]

6. Murray J. D. (2002), Mathematical biology (Berlin: Springer).         [ Links ]

[71985Volkenshtein]

7. Volkenshtein M. V. (1985), Biofísica (Moscú: Mir).         [ Links ]

[81974Field & Noyes]

8. Field R. J. & Noyes R. M. (1974), J. Chem. Phys. 60, 5, 1877.         [ Links ]

[91992Ruoff]

9. Ruoff P. (1992), J. Phys. Chem-US. 96, 23, 9104.         [ Links ]

[101997Johnson et al. Johnson, Scott & Thompson]

10. Johnson B. R., Scott S. K. & Thompson B. W. (1997), Chaos 7, 2, 350.         [ Links ]

[111987Argoul et al. Argoul, Arneodo, Richetti & Roux]

11. Argoul F., Arneodo A., Richetti P. & Roux J.-C. (1987), J. Chem. Phys. 86, 6, 3325.         [ Links ]

[121981Hudson & Mankin]

12. Hudson J. L. & Mankin J. C. (1981), J. Chem. Phys. 74, 11, 6171.         [ Links ]

[131980Janz et al., Janz, Vanecek & Field]

13. Janz R. D., Vanecek D. J. & Field R. J. (1980), J. Chem. Phys. 73, 7, 3132.         [ Links ]

[141981Kepper & Boissonade]

14. - de Kepper P. & Boissonade J. (1981), J. Chem. Phys. 75, 1, 189.         [ Links ]

[151991Schneider & Münster]

15. Schneider F. W. & Münster A. F. (1991), J. Phys. Chem-US. 95, 6, 2130.         [ Links ]

[161990Györgyi et al. Györgyi, Turángy & Field]

16. Györgyi L., Turángy T. & Field R. J. (1990), J. Phys. Chem-US. 94, 18, 7162.         [ Links ]

[171991Györgyi et al. Györgyi, Rempe & Field]

17. Györgyi L., Rempe S. L. & Field R. J. (1991), J. Phys. Chem-US. 95, 8, 3159.         [ Links ]

[181991Györgyi & Field]

18. Györgyi L. & Field R. J. (1991), J. Phys. Chem-US. 95, 17, 6594.         [ Links ]

[191992Györgyi et al. Györgyi, Field, Noszticzius, McCormick & Swinney]

19. Györgyi L., Field R. J., Noszticzius Z., McCormick W. D. & Swinney H. L. (1992), J. Phys. Chem-US. 96, 3, 1228.         [ Links ]

[201992Györgyi & Field]

20. Györgyi L. & Field R. J. (1992), Nature 355, 808.         [ Links ]

[212011Freire & Gallas Freire & Gallas]

21. Freire J. C. & Gallas J. A. C. (2011), Phys. Chem. Chem. Phys. 13, 26, 12191.         [ Links ]

[221995Mazzotti et al. Mazzotti, Morbidelli & Serravalle]

22. Mazzotti M., Morbidelli M. & Serravalle G. (1995), J. Phys. Chem-US. 99, 13, 4501.         [ Links ]

[231984Crowley & Field]

23. Crowley M. F. & Field R. J. (1984), J. Phys. Chem-US. 88, 4, 762.        [ Links ]

 

File translated from T_EX by T_TH, version 3.89.
On 30 Oct 2013, 16:09.