Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
Compartir
Revista Boliviana de Física
versión On-line ISSN 1562-3823
Revista Boliviana de Física v.23 n.23 La Paz feb. 2013
Análisis Estocástico Sobre Registros de Temperatura
STOCHASTIC ANALYSIS OF TEMPERATURE DATA
V. M. Peñafielf; M. Andradef
Abstract
Se propone una simulación Monte Carlo simple (con modelo gaussiano) para registros de temperatura media diaria sobre territorio boliviano. Las series temporales empíricas, conteniendo temperaturas máxima y mínima, se reducen a series de temperatura promedio y se descomponen para extraer los parámetros de la simulación, mostrando los resultados para cinco estaciones colocadas aproximadamente sobre los ejes EO y NS de Bolivia. Se hizo énfasis asimismo en la determinación de la tendencia lineal de los datos empíricos ya que dicha tendencia es un indicador directo del cambio en la temperatura media local que, para las últimas dos décadas, sugiere un calentamiento equivalente a unos 2 grados por siglo sobre el territorio boliviano.
Descriptores: Análisis de series temporales - Métodos de Monte Carlo
Código(s) PACS: 05.45.Tp, 05.10.Ln
We propose a simple Monte Carlo simulation (with a Gaussian model) for the average daily temperature data in the Bolivian territory. The empirical time series with maximum and minimal temperatures are reduced to a series of average temperature and then they are decomposed to extract the simulation parameters; the results are shown for five stations located approximately along the east-west and north-south axes in Bolivia. We also determined the linear trend of the empirical data; this trend is a direct indicator of the average local temperature change which suggests a warming effect (for the two last decades) equivalent to 2 degrees per century in the Bolivian territory.
Subject headings: Time series analysis - Monte Carlo methods
1 Introducción
La temperatura es una de las variables más usadas para el estudio del cambio climático, pero también para el seguimiento y anticipación de todas las actividades relacionadas con el clima.
En primera instancia interesa el comportamiento de la temperatura media diaria antes que el estudio de los valores extremos. Por ello, se ha construido registros limpios (regularizados en los lugares con mediciones faltantes) para la temperatura media T(t)=[Tmax(t)−Tmin(t)]/2. Todo el trabajo posterior está realizado sobre tales registros.
El propósito es el de aplicar, para cada estación de registro, un modelo simple que permita anticipar y examinar el comportamiento de la temperatura a partir de los datos disponibles. y también, dentro de límites razonables, contestar la interrogante, siempre ilustrativa, de si los datos muestran tendencias positivas (calentamiento) o negativas (enfriamiento).
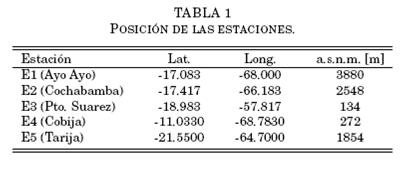
De los registros disponibles para el presente trabajo, que provienen de 40 estaciones sobre territorio boliviano (), se ha elegido una muestra de 5, más o menos a lo largo de los ejes transversal y longitudinal de este territorio (Tabla 1.), cubriendo también las tres zonas climáticas más representativas (altiplano, valles y llanos). Estas tres zonas tienen diferentes influencias térmicas aleatorias desde el punto de vista estadístico. Por esto, es interesante ver si el método de simulación muestra un comportamiento medio diferente para cada una de ellas.
Finalmente, aceptando que la inclinación de la recta de regresión sobre los registros completos proporciona una primera estimación de la variación térmica temporal, se ha empleado el conjunto de las 40 estaciones para determinar una razonable aproximación a ese parámetro sobre el territorio boliviano durante el lapso estudiado.
2 Descomposición de las Series Empíricas

Las series temporales constan de 7304 valores cada una, correspondientes a 20 años, desde el 1 de Enero de 1989 hasta el 31 de Diciembre de 2008.
Se supone que estas series son susceptibles de ser descompuestas en la forma aditiva
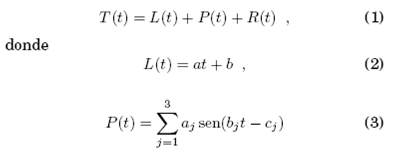
(suma de 3 funciones armónicas sólo para fines del presente trabajo) y R(t) una componente de ruido aleatorio.
La función L(t) resulta, obviamente, de un ajuste por mínimos cuadrados sobre la serie temporal completa y sus coeficientes aparecen en la tabla 2. La componente periódica P(t), para la descomposición, es la antitransformada de Fourier del espectro obtenido aislando los tres picos más distinguibles (Fig. 3) de la transformada de {T(t)−L(t)} (Fig. 2.).
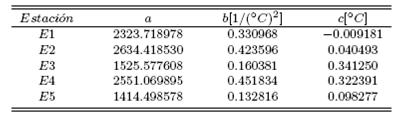
El ajuste por mínimos cuadrados de la ec. (2) sobre el registro de la antitransformada (que se muestra en la Fig. 4.) se usa posteriormente para la simulación con los valores que aparecen el la tabla 3. Un procedimiento enteramente similar para las otras estaciones lleva a los resultados mostrados en las tablas 4., 5., 6. y 7. La inspección de los valores indica que la suposición inicial de aditividad de las funciones (1), (2) y (3) es aproximada pero, como se verá, estadísticamente suficiente.
Finalmente, restando el registro de la antitransformada del de {T − L}, se obtiene la serie correspondiente al ruido aleatorio R (Fig. 5.), bastante complejo, como se aprecia. Las complejidades de este registro, sin embargo, parecen estar concentradas en los valores extremos de temperatura. Para ninguna de las
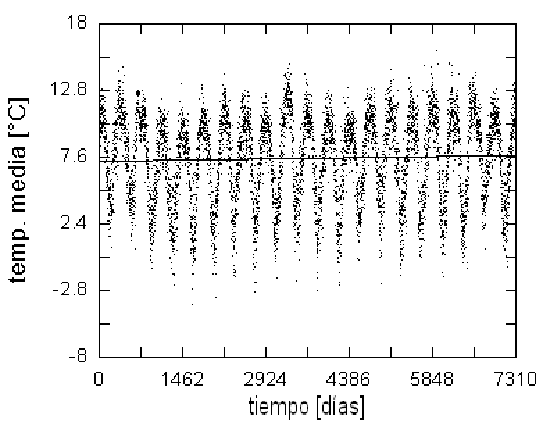
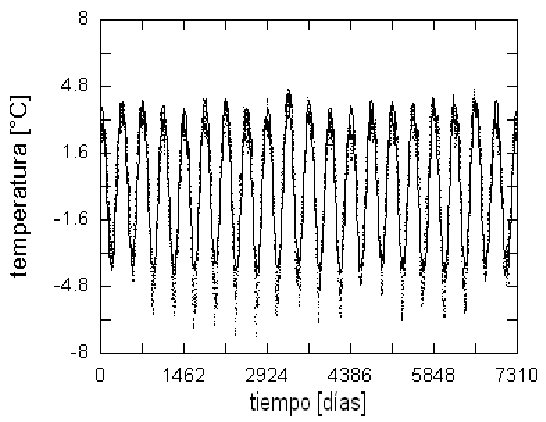
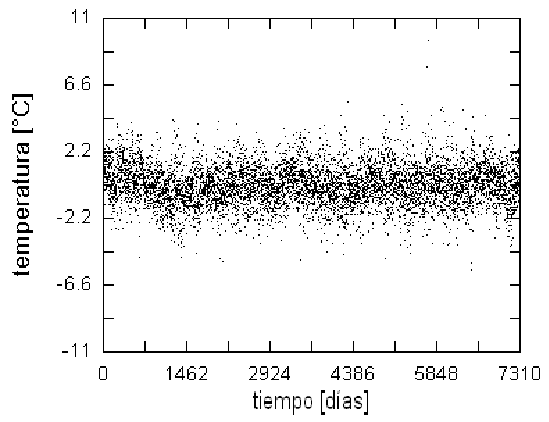
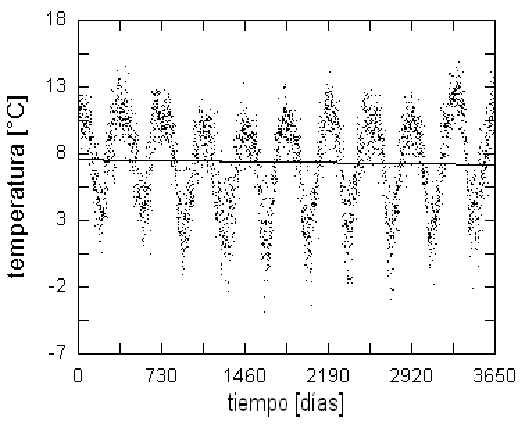
Figure 1: Datos de temperatura media provenientes de E1 (Ayo Ayo) desde el 1 de Enero de 1989 hasta el 31 de Diciembre de 2008. Aparte de la tendencia lineal (la recta at+b ajustada por cuadrados mínimos), es notoria la periodicidad anual afectada por ruido estocástico.
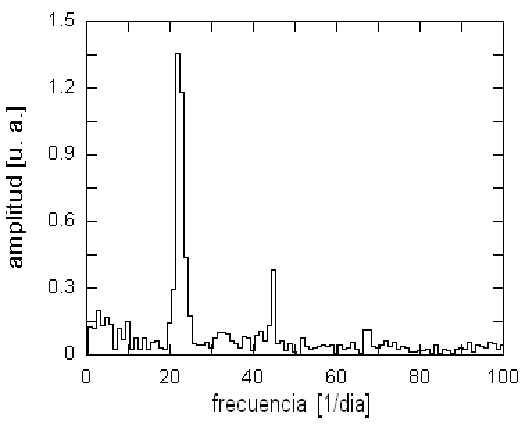
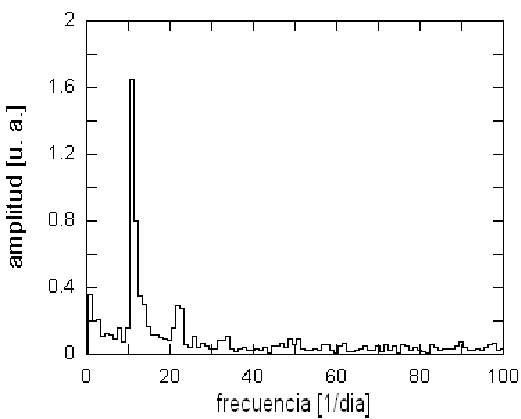
Figure 2: Transformada rápida de Fourier (TRF) sobre los datos de la Fig.1. menos los generados por la recta de regresión. el pico mayor corresponde al obvio período anual 8192/23=356 < T < 8192/22=372.36. Los picos más pequeños son, probablemente, resonancias; aunque es posible interpretarlos también como comportamientos similares (pero con valores diferentes) entre estaciones (0.52 y 0.33 de año, respectivamente).
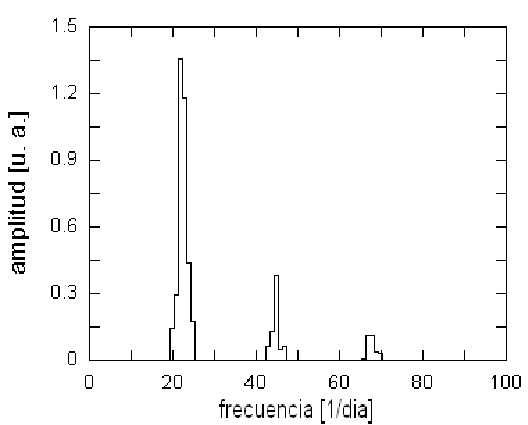
Figure 3: Filtro aplicado para aislar los tres picos más conspicuos de la TRF de la Fig. 2.
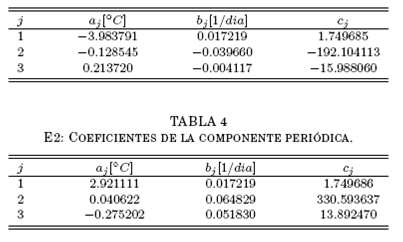
Figure 4: Antitransformada del espectro mostrado en la Fig. 2. La línea continua corresponde al ajuste por mínimos cuadrados de la ec. 2.
estaciones el ajuste (m.c.) gaussiano
![]()
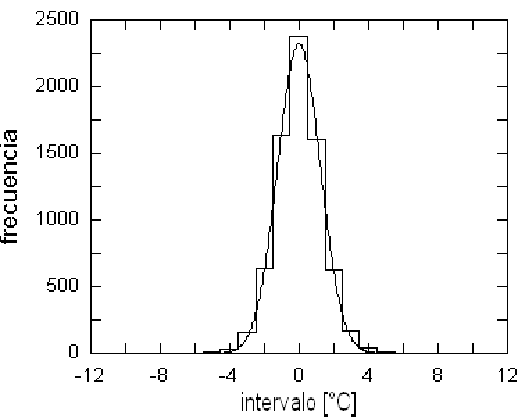
a los histogramas de frecuencias (Fig. 5. para E1 pasa la prueba ji cuadrada a .95.
3. COMPONENTE ALEATORIA
La desviaci ´on de la distribuci ´on gaussiana es más evidente en figura 7. que corresponde al histograma de frecuencias de la componente aleatoria para la estación E5.
La actividad en los extremos ahora es muy evidente.
Es posible integrar numéricamente el histograma empírico para obtener una curva de ajuste (Fig. 8.) y usarla mediante sorteo Monte Carlo para generar ruido aleatorio simulado, calcular nuevamente el histograma de frecuencias y compararlo con el original de la figura 7. El resultado aparece en la figura 9. con un coeficiente de correlación r = 0.941.
Por otra parte, la simulación puramente gaussiana de esta componente aleatoria, usando los parámetros b y c de la tabla 8. para E5, agrupada nuevamente en una serie de frecuencias y comparada con el original de la Fig. 7. se resume en la figura 10. El coeficiente de correlación es, ahora, r = 0.994.
Es claro que la influencia de valores extremos de temperatura sobre el comportamiento estadístico de los registros empíricos requiere un estudio separado. Consecuentemente, gran parte de las propiedades de las series temporales de temperatura media son susceptibles de ser simuladas con el supuesto de que la componente aleatoria R es, aproximadamente, gaussiana.
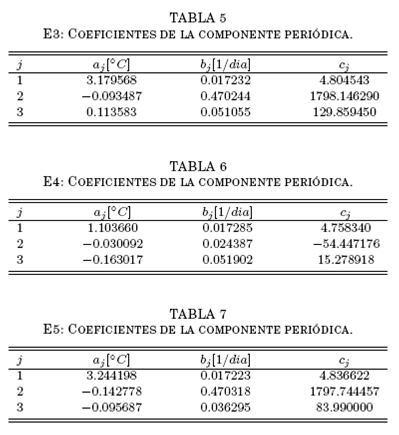
Figure 5: Ruido aleatorio aislado sustrayendo el registro correspondiente al la Fig. 3. de {T−L} para la estación E1.
4 Simulación
Como se ha supuesto inicialmente la aditividad (1), el procedimiento de descomposición descrito permite extraer los parámetros necesarios para producir rápidamente registros estadísticamente equivalentes a los empíricos. Las series simuladas calculan la ec. (1) con los parámetros de la tabla 2., le suman los armónicos de la ec. (2) con los coeficientes de las tablas 3. a 7. y, finalmente, se añade ruido aleatorio producido por el método Monte Carlo y el de Box-Muller (),
Table 8: Parámetros del ruido gaussiano.
>
(a)
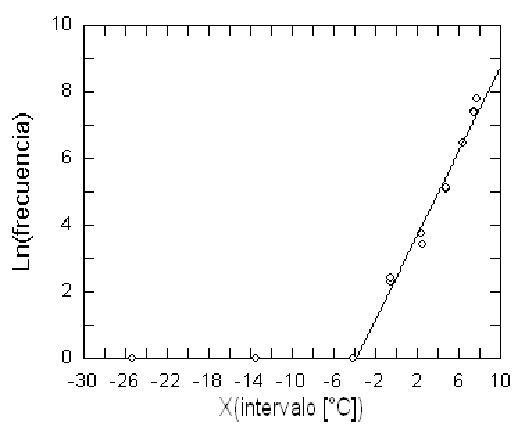
(b)
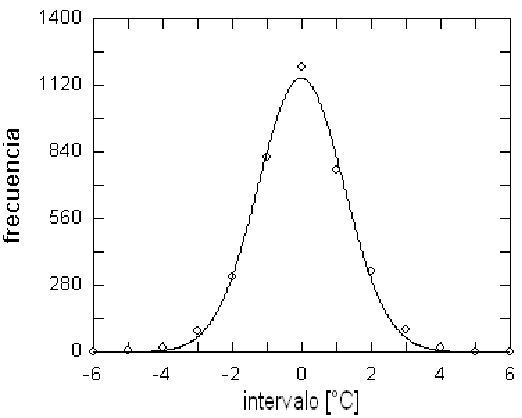
Figure 6: (a) Histograma de frecuencias de los datos usados para construir la Fig.4. La curva gaussiana corresponde a un ajuste m.c. de la ecuación (4). (b) Gráfico lineal ln(frecuencias) vs. X(intervalos)= −b(∆T − c)2 + ln(a), correspondiente a la fig. 6. La recta de ajuste permite apreciar que las diferencias con la gaussiana provienen principalmente de las colas (valores extremos de temperatura).
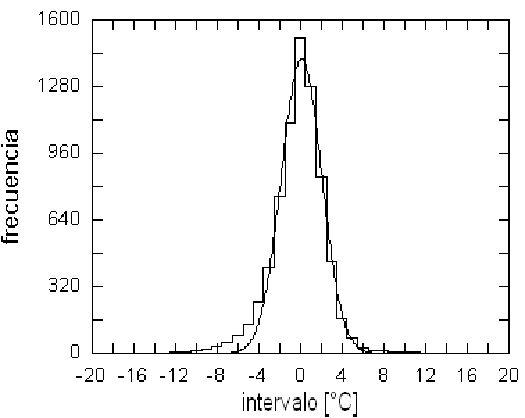
(a)
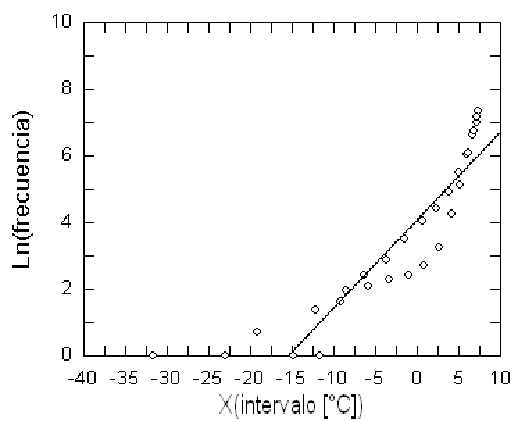
(b)
Figure 7: (a) Histograma de frecuencias correspondiente al ruido aleatorio separado del registro de temperatura media para la estación E5 usando el método descrito para E1. (b) Gráfico lineal ln(frecuencias) vs. X(intervalos) para E5, como el de la fig. 6a. Las desviaciones respecto de la recta de ajuste son ahora más pronunciadas y la asimetría de la distribución empírica es realmente muy notoria.
esto es, el sorteo de dos números aleatorios ξ1 y ξ2 y el empleo de la relación
donde a y b son los parámetros de ajuste a curvas (4) como las de las figuras 6. y 7. y que se detallan en la tabla 8. para cada una de las estaciones.
El sorteo de los números ξ se hizo usando una rutina adaptada del Mersenne Twister () para el ensamblador de 32 bites, lenguaje en el cual todos las operaciones y algoritmos fueron realizados.
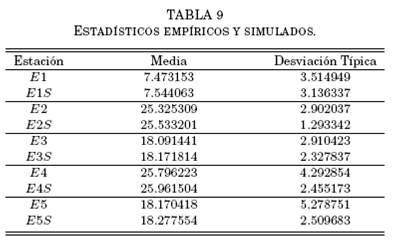
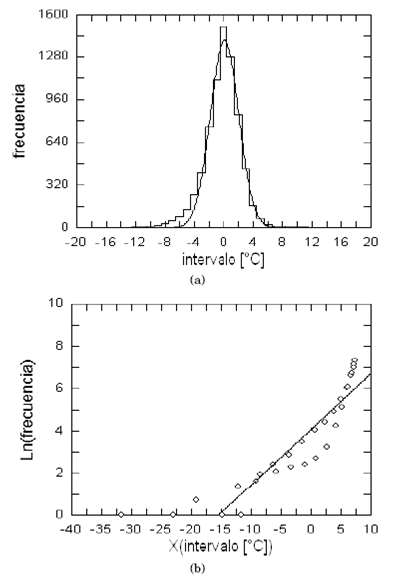
FIG. 7. (a) Histograma de frecuencias correspondiente al ruido aleatorio separado del registro de temperatura media para la estación E5 usando el m´etodo descrito para E1. (b) Gráfico lineal
ln(frecuencias) vs. X(intervalos) para E5, como el de la fig. 6a.
Las desviaciones respecto de la recta de ajuste son ahora más pronunciadas y la asimetría de la distribución empírica es realmente muy notoria.
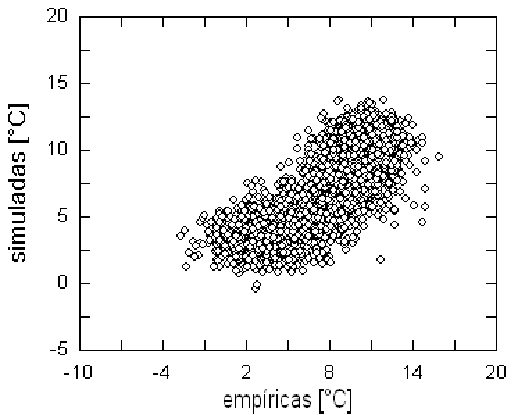
El resultado es la generación de series temporales que imitan muy aproximadamente el comportamiento de sus correlativas experimentales. Así, la tabla 9. es la comparación de los valores medios y desviaciones típicas de los registros originales y sus simulaciones. Como ya se ha enfatizado, aunque los valores medios son muy próximos (como era de esperarse), la dispersión es siempre mayor en los empíricos por la presencia de ráfagas de temperaturas extremas que no están presentes en los subrogados.
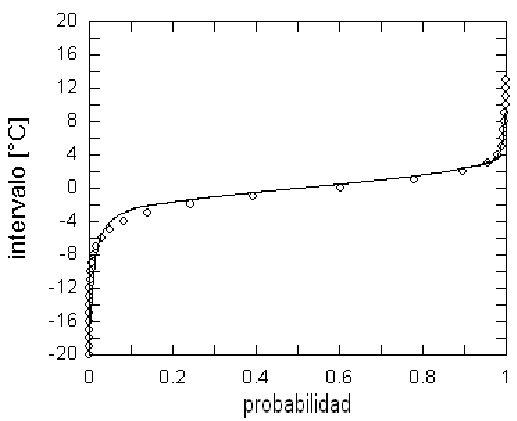
Figure 8: Distribución de probabilidad acumulativa, construida numéricamente a partir del histograma empírico (Fig. 7.).
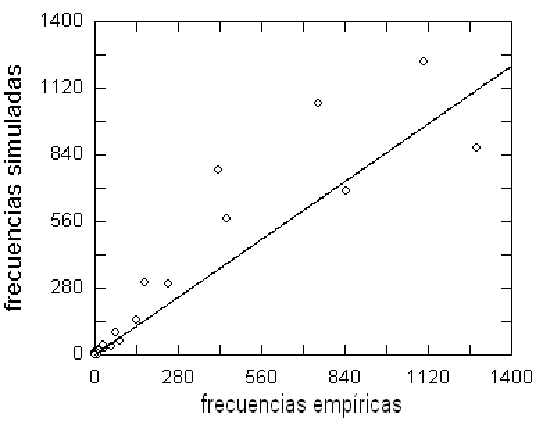
Figure 9: Correlación entre frecuencias simuladas con ruido producido por la curva de la figura 8. y las frecuencias empíricas de la figura 7. Mejor para valores bajos (saltos grandes de temperatura).
Para estimar la capacidad de predicción del procedimiento, se lo aplicó a la mitad de los datos de cada registro -que cubre una década- y se ha comparado el resultado con la década empírica siguiente. Por ejemplo, para los datos de la primera mitad del registro E1 que se muestran en la figura 11., aislando los tres picos de la transformada de {T−L} (Fig.12.), tomando la antitransformada, restándola de {T−L} y calculando el histograma de frecuencias que corresponde a la componente aleatoria (Fig. 13.), se obtiene todos los parámetros para la simulación propuesta.
El único parámetro que debe ser ajustado, para simular la segunda década usando ajustes a la primera, es la temperatura inicial, la cual es ahora b+3650a. El resultado se compara con la segunda mitad del registro E1 rindiendo un coeficiente de correlación r=0.784 y se muestra en la figura 15.
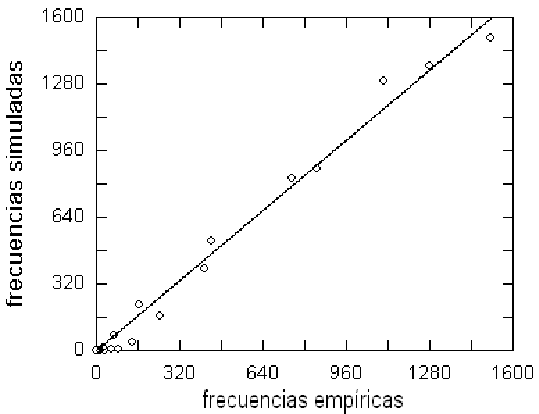
Figure 10: Correlación entre frecuencias simuladas con ruido puramente gaussiano y las frecuencias empíricas de la Fig. 7. Mejor para valores altos (saltos pequeños de temperatura.
Figure 11: Datos de temperatura media correspondientes a la primera década del registro E1. Se muestra la tendencia lineal (¡negativa!).
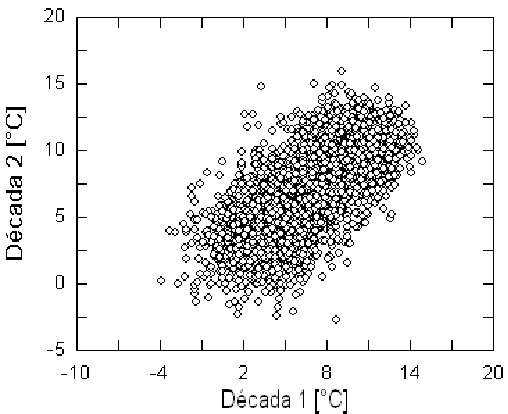
Como referencia para evaluar la utilidad de estas simulaciones anticipadas, es necesario tener en cuenta que, en general, las series temporales de temperatura son, no obstante su regularidad, fuertemente influidas por la componente aleatoria. Así, el coeficiente de correlación entre las dos mitades del registro empírico E1 es sólo r = 0.722 y su diagrama de correlación lo refleja gráficamente (Fig. 14.). La simulación se comporta, en este sentido, ligeramente mejor y se considera que, como instrumento de trabajo, puede emplearse como un registro subrogado de E1.
5 Tendencia Lineal
La suposición inicial relativa a la descomposición simplemente aditiva de {L}, {P} y {R} es, por supuesto, sólo una conveniente aproximación. Esto se aprecia de inmediato, por ejemplo, en el ruido remanente de la figura 4. no obstante la estrechez del filtro aplicado.
Figure 12: TRF a los datos de la Fig 11. menos la tendencia lineal. Se tiene básicamente las mismas características consideradas para la Fig. 7.
Figure 13: Histograma de la componente aleatoria de la serie correspondiente a la primera década del registro E1. La curva de ajuste proporciona los parámetros para generar la serie simulada de la segunda década.
Figure 14: Diagrama de correlación entre datos empíricos de las primera y segunda décadas para la estación E1.
Figure 15: Diagrama de correlación entre datos simulados (con parámetros de la primera década) y datos empíricos de la segunda década para la estación E1. El ligero alargamiento, comparando con la Fig. 13. indica mejor correlación.
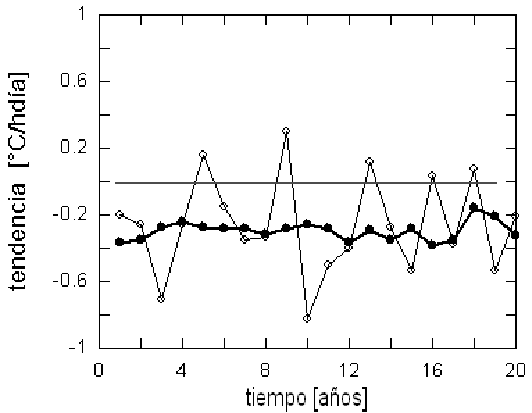
Figure 16: Evolución anual de la tendencia lineal (estación E1); los puntos llenos corresponden a los valores simulados y son, por supuesto, menos dispersos que los empíricos.
Por otra parte, una inspección a los valores del parámetro a (inclinación de la tendencia) en la tabla 2. podría implicar un calentamiento local de 1.9 ±0.5 [°C/siglo] aproximadamente. Se verifica que la muestra es significativa, pues, el valor calculado para las 40 estaciones disponibles es 2.04 ±0.60 [°C/siglo].
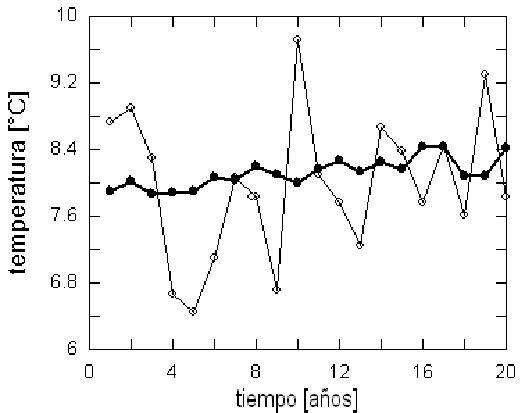
Sin embargo, las fluctuaciones en tiempo y lugar se ponen de manifiesto mediante un análisis gráfico de los registros. Así, la figura 16. muestra las tendencias -parámetro a de la ec. (1)- calculadas anualmente para los registros empírico y simulado de la estación E1. Nuevamente la presencia de ráfagas de temperaturas extremas se manifiesta en las abruptas fluctuaciones de las tendencias experimentales; contrastando la homogeneidad de la evolución temporal de las tendencias simuladas. Como consecuencia, la evolución temporal de las temperaturas medias iniciales anuales exhibe también la misma característica (Fig. 17.).
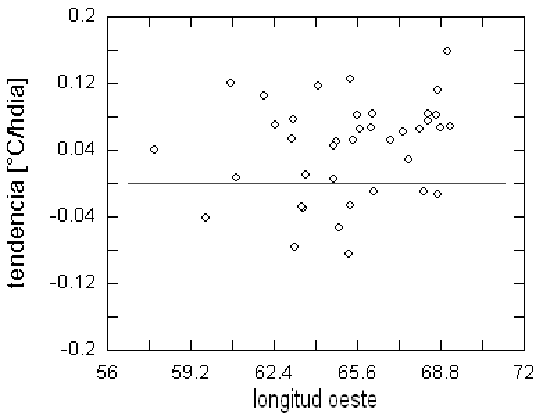
Extendiendo el análisis a las 40 estaciones disponibles, se observa (figuras 18. y 19.) la ausencia de sistematicidad en los valores de la tendencia lineal tanto en latitud sur cuanto en longitud oeste, que caracterizan las localizaciones geográficas
Figure 17: Evolución anual de la temperatura media inicial (estación E1); los puntos llenos corresponden a los datos simulados y muestran menor dispersión.
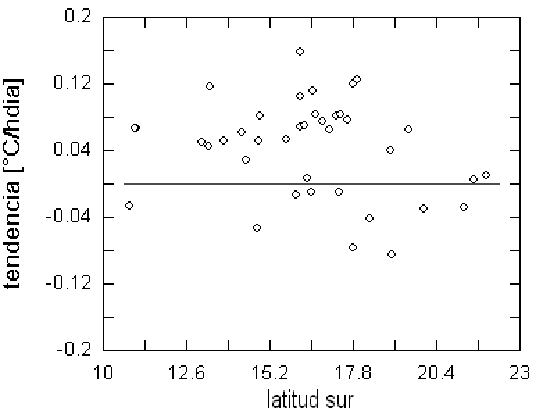
Figure 18: Tendencia por latitud (Sur). No parece haber correlación por zona de las estaciones.
de las estaciones dentro del territorio boliviano. La distribución aleatoria, aunque con preponderancia de valores positivos (75%) es una clara indicación de influencias climáticas locales, esporádicas pero intensas (eventos extremos).
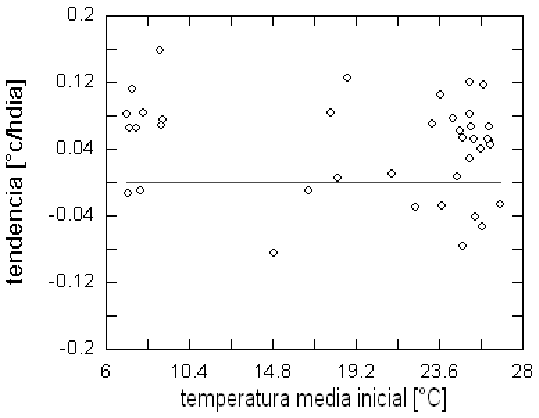
Finalmente, la figura 20. indica que las zonas climáticas (caracterizadas por el valor de las temperaturas medias iniciales) tampoco tienen especial nivel de calentamiento local aunque, estadísticamente al menos, se observan estaciones que muestran un incremento de la temperatura media en todas las regiones.
Figure 19: Tendencia por longitud (oeste). No se advierte correlación alguna en tendencias positivas ni negativas.
Figure 20: Tendencia lineal por temperatura media inicial. Hay, en general, preponderancia de tendencia positiva, pero es evidente que es mayor en la parte de bajas temperaturas (zona altiplánica).
6 Conclusiones
Hay bastante evidencia que asocia la anormalidad de la componente aleatoria en series temporales de temperatura con el comportamiento de las máximas o mínimas (v. g. [32002Harmel et al.Harmel, Richardson, Hanson, & Johnson]). Se ha intentado aquí mostrar que, dejando de lado el estudio de esos extremos de temperatura, la región de fluctuaciones pequeñas puede aproximarse a ruido gaussiano, obteniendo así registros simulados estadísticamente comparables con los empíricos. El análisis de valores extremos requiere, sin duda, un tratamiento independiente en términos de lo expuesto en el presente trabajo.
Tampoco se ha considerado el asociar la evolución temporal con aplicaciones comunes, por ejemplo a la agricultura, mediante el tratamiento de derivadas climáticas (). La intención es, más bien, la de construir un modelo sencillo, fácil de ser utilizado como un procedimiento de trabajo para comparar los cambios a mediana escala respecto de ciertas propiedades esperadas, caracterizadas por parámetros extraídos de los mismos registros empíricos; el modelo es, por tanto, sólo localmente aplicable (para cada punto de medición).
Con tales restricciones, una primera aproximación es el concepto de composición aditiva dada por la ec. (1), con R(t) directamente considerado como ruido gaussiano.
Admitido esto, se encuentra que la presencia de fluctuaciones extremas se reflejará, finalmente, en inestabilidad de la tendencia lineal, objeto ya de exhaustivos exámenes (). Las oscilaciones irregulares de este parámetro en el dominio temporal terminan en una dispersión espacial, aunque con una notoria preponderancia de valores positivos.
El resultado final, < a > = 2.04 ±0.60 [°C/siglo] indica que, en los últimos 20 años, existe una tendencia al incremento de la temperatura media (calentamiento local no sistemático) en el territorio boliviano.
References
[12005Bari et al.Bari, Driss, Mraoua, & Mohammed]
1. Bari, Driss, Mraoua & Mohammed (2005), Scandinavian Journal of Statistics 4, 746. [ Links ]
2. Box G. E. P. & Muller M. E. (1958), Ann. Math. Statist. 29, 610. [ Links ]
[32002Harmel et al.Harmel, Richardson, Hanson, & Johnson]
3. Harmel R. D., Richardson C. W., Hanson C. L. & Johnson G. L. (2002), J. Appl. Meteor. 41, 544. [ Links ]
4. Hurrell J. W. (1995), Science 264, 676. [ Links ]
5. Matsumoto M. & Nishimura T. (1998), ACM Transactions on Modeling and Computer Simulation 8, 3. [ Links ]
6. SENAMHI (2010), Servicio Nacional de Meteorología e Hidrología (Comunicación Privada) [ Links ]
File translated from TEX by TTH, version 3.89.
On 30 Oct 2013, 14:56.