Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Boliviana de Física
versión On-line ISSN 1562-3823
Revista Boliviana de Física v.22 n.22 La Paz 2013
CONDICIONES DE SINCRONIZACIÓN DE DOS OSCILADORES MÓVILES
SYNCHRONIZATION CONDITIONS OF TWO MOBILE OSCILLATORS
R. O. E. Bustos Espinozaf
G. M. Ramírez Ávilaf
Resumen
Se estudia el problema de la sincronización de dos osciladores móviles escogiendo como prototipo de oscilador a un mapa logístico tanto por su simplicidad matemática como por su riqueza de comportamiento. Se proponen dos esquemas de acoplamiento: uno de tipo campo medio y el otro dependiente de la distancia. El movimiento de los osciladores cambia de acuerdo a una regla impuesta que está en relación con el grado de sincronización del sistema y con una distancia umbral que evite la colisión de los osciladores. Se encuentra una tendencia a facilitar la sincronización debida al movimiento de los osciladores. Se dan posibles aplicaciones de este tipo de sistemas.
Descriptores: Dinámica no lineal y caos - sincronización y osciladores acoplados
Código(s) PACS: 05.45.-a, 05.45.Xt
Abstract
We study the problem of synchronization in motile oscillators. We choose as the prototypical oscillator of the system a logistic map due to both its mathematical simplicity and its rich dynamical behavior. We propose two coupling schemes: the first is a mean field type and the second is a distance dependent one. The motion of the oscillators is related to a specific rule in relationship with the synchronization degree of the system and a threshold distance which avoid the collision between the oscillators. Our results show a tendency for enhanced synchronization due to the motion of the oscillators. We point out some possible applications of this kind of systems.
Subject headings: Nonlinear dynamics and chaos - synchronization and coupled oscillators
1 Introducción
La sincronización es un fenómeno omnipresente en la naturaleza y cuyo estudio ha tomado gran importancia tanto desde el punto de vista teórico como experimental, tal como lo indican [222003Pikovsky & Maistrenko]. Por otra parte, fruto de la investigación básica, se encontraron diferentes aplicaciones, siendo una de las más importantes el encriptado y desencriptado de señales descrito en [211995Pérez & Cerdeira,391996Yang & Chua,401997Yang et al.Yang, Wu, & Chua] y en general, aspectos relacionados a comunicación de señales expuestos por [152007Lin & Tsai,162009López-Gutiérrez et al.López-Gutiérrez, Posadas-Castillo, López-Mancilla, & Cruz-Hernández]. Además, la sincronización se manifiesta fuertemente en sistemas biológicos, como lo resalta [132012Janson], tales como en luciérnagas, cuya descripción se da en [51935Buck,121971Hanson et al.Hanson, Case, Buck, & Buck,41976Buck & Buck], en cigarras, como lo muestra [352002Sueur], en saltamontes, cuyo estudio se da en [341990Sismondo,101993Greenfield & Roizen], en ranas, como lo ana-liza [12009Aihara] y en sistemas neuronales tal como se menciona en [202008Nowotny et al.Nowotny, Huerta, & Rabinovich] bajo diferentes circunstancias y condiciones tales como cuando las neuronas forman una red tipo "mundo pequeño", aspecto estudiado por [382007Wei & Luo] o una red "libre de escala", lo que es analizado por [112005Grinstein & Linsker,32009Batista et al.Batista, Batista, de Pontes, Lopes, & Viana].
El estudio del movimiento de elementos de un sistema, ha merecido la atención en dinámica no lineal y varios trabajos acerca del carácter colectivo de este fenómeno fueron realizados tomando diferentes enfoques. Así, la consideración hecha por [331996Shimoyama et al.Shimoyama, Sugawara, Mizuguchi, Hayakawa, & Sano] de una interacción entre elementos móviles dependiente de una distancia mutua óptima permite describir situaciones tales como caminatas rectas, ondulantes y aleatorias; así como movimiento en enjambres. El mo-delo de partículas auto-propulsadas y su comportamiento colectivo frente a ruido es analizado por [72000Czirok & Vicsek] tanto con un modelo discreto como con uno continuo. La utilización de mapas cuadráticos por [322003Shibata & Kaneko] para estudiar la dinámica interna de osciladores caóticos ha permitido describir el comportamiento dinámico de los denominados gases de mapas acoplados, en los cuales, la posición de los elementos móviles está determinada por una fuerza que depende de la dinámica interna de cada uno de los osciladores. La descripción y cuantificación de un comportamiento colectivo de osciladores móviles cuya dinámica interna está basada en un mapa logístico es formulada por [92011García Cantú Ros et al.García Cantú Ros, Antonopoulos, & Basios] para lo cual utilizan un índice de agrupamiento que toma en cuenta simultáneamente el grado de agrupamiento espacial así como el alineamiento de las velocidades de los elementos móviles. El estudio de la sincronización de osciladores fotocontrolados móviles, similares en comportamiento a las luciérnagas, ha sido planteado y desarrollado por [242004Ramírez Ávila]. La sincronización en osciladores de "integración y disparo" en la situación simple de interacciones de tipo maestro-esclavo es descrita en [312010Sarkar], encontrándose que la sincronización global del sistema es más fácilmente alcanzada cuando los osciladores tienen un movimiento aleatorio. El acoplamiento dependiente del tiempo en osciladores móviles en los cuales se tienen alternativamente interacciones atractivas y repulsivas es analizada por [412004Zanette & Mikhailov], encontrándose transiciones entre estados ordenados y desordenados mediados por un régimen de agrupamiento dinámico.
En este trabajo, se consideran osciladores móviles en interacción, entendiendo que un oscilador, es un agente que puede presentar comportamiento periódico, cuasiperiódico o caótico; es por ello que asociamos a la dinámica interna de cada oscilador, un mapa logístico. Presentamos una caracterización de la sincronización de dos osciladores móviles con las propiedades citadas en el anterior párrafo y que pueden moverse aleatoriamente en un plano pero con ciertas restricciones tanto en lo referente a la distancia entre los mismos como al grado de sincronización que estos exhiben. Se consideran dos tipos de acoplamiento, uno en el que la intensidad del mismo no varía con el tiempo ni con la posición y otro en el que la distancia entre los osciladores juega un rol primordial y que varía con el inverso del cuadrado de la distancia entre los osciladores.
El artículo está organizado de la siguiente ma-nera: en §2, se exponen las principales características de un mapa logístico y del acoplamiento entre dos de estos mapas. Se detallan los tipos de acoplamiento y se dan las condiciones para el movimiento de los osciladores; por otra parte, se define el factor que determina la sincronización del sistema. Los resultados del trabajo se dan en §3 tanto para el acoplamiento que permanece constante (tipo campo medio) §3.1 como para el que depende de la distancia entre los osciladores §3.2; así mismo, se procede a hacer una comparación para resaltar las propiedades que introduce el movimiento de los osciladores en el sistema. Finalmente, en §4 se señalan las conclusiones y perspectivas de la presente investigación.
2 Modelo
El mapa logístico, se representa por una ecuación en diferencias formulada por [171976May] que se deriva de una ecuación, propuesta en el s. XIX por [371838Verhulst] que describe la dinámica de una población considerando aspectos tales como la tasa de nacimiento per capita y la capacidad de carga, aspectos explicados por [192002Murray]. Este mapa ha sido utilizado ampliamente en diferentes disciplinas sobre todo por la simplicidad que ofrece y al mismo tiempo la gran variedad de comportamientos que presenta. Por esta razón, se escogió como modelo para cada uno de los osciladores un mapa logístico dado por:
![]()
donde μ es el parámetro de control que determina el comportamiento del mapa tal como se puede ver en el diagrama de bifurcación de la Fig. 1(a), en el cual se distinguen las regiones: de extinción (0 ≤ μ ≤ 1), estacionaria (μ < 3), período 2k con k ∈ \mathbbZ+ y 3 ≤ μ < μ∞, siendo μ∞=3.569945672 el denominado punto de acumulación (Fig. 1(b)), cuasiperiódica y caótica; también se presenta intermitencia por ejemplo en el intervalo 3.8264 < μ < 3.8304 tal como se indica en [142008Landau et al.Landau, Páez, & Bordeianu] (Fig. 1(c)), donde des-pués de que el sistema aparece como estable, posteriormente se torna inestable para luego volver a la estabilidad, repitiéndose este comportamiento de manera indefinida. Es de hacer notar que la transición hacia el caos ocurre de manera que para ciertos valores de los parámetros, el sistema no presenta ninguna regu-laridad y es fuertemente dependiente de las condiciones iniciales como se señala en [291990Rasband]; además, una vez que el sistema alcanza el regimen caótico, se puede salir del mismo a través de ventanas de período impar tal como lo demuestran analíticamente [301995Saha & Strogatz] (Fig. 1(c)), para volver nuevamente a través de una cascada de bifurcaciones a regiones caóticas (Fig. 1(d)).
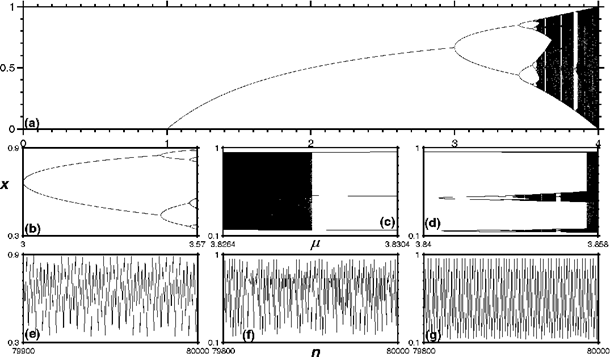
Figure 1: Diagramas de bifurcación para el mapa logístico regido por la Ec. (1): (a) en todo el espectro de valores posibles de μ; (b) en la región de desdoblamiento de período 2k; (c) en el intervalo 3.8264 < μ < 3.8304, donde luego de una región caótica, se presenta una ventana de período 3; (d) cascada de desdoblamiento de período impar. Series temporales para valores de μ contenidos en (b)-(d): (e) 3.5699, (f) 3.8264, (g) 3.8568.
En la Fig. 1(e)-(g) se muestran las series de tiempo para valores del parámetro de control contenidos en los diagramas de la Fig. 1(b)-(d): (e) μ = 3.5699, (f) μ = 3.8264 y (g) μ = 3.8568.
Para nuestro estudio de la sincronización de dos osciladores móviles, consideramos el acoplamiento de dos mapas logísticos, cuyas ecuaciones son:

donde los superíndices identifican a los osciladores y los subíndices representan la evolución temporal. La intensidad de acoplamiento, que asumimos simétrica, viene dada por β, para la cual consi-deramos dos casos:
Acoplamiento constante.
Introducido por razones de simplicidad puesto que, en este caso, la intensidad de acoplamiento no varía aunque las posiciones de los osciladores se modifiquen. Si se considera que los osciladores permanecen siempre acoplados a pesar de lo alejados que puedan estar; se tendrá β = constante, lo que es equivalente a una situación en la que los osciladores no se mueven. Resaltamos el hecho de que aunque se tenga una situación muy simple, la caracterización completa de la misma, requiere un cálculo numérico intenso.
Acoplamiento dependiente de la distancia.
La elección de este tipo de acoplamiento está basado en el hecho de que existen sistemas de osciladores cuyo acoplamiento depende de la distancia β = β(d12) (ver p. ej. [282003Ramírez Ávila et al.Ramírez Ávila, Guisset, & Deneubourg]). Esta dependencia, en su forma más simple, tiene la forma:
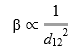
Siendo d12, la distancia entre los osciladores 1 y 2.
Por otra parte, se debe tener en cuenta que para un oscilador libre, el valor de x está comprendido en el intervalo [0, 1]; sin embargo, dependiendo del valor del acoplamiento β, en principio, el valor de x podría salir del intervalo anteriormente mencionado por lo que imponemos la condición:
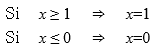
Ahora, para estudiar el movimiento de los osciladores, consideramos que cada oscilador es des-crito por el vector →r que tiene en cuenta tanto la dinámica del oscilador en la variable x como la posición del mismo en el plano Y−Z. Así:
![]()
Para la cuantificación de la sincronización se define el factor de sincronización σ dado por:
![]()
el cual permite identificar la sincronización (σn → 0) o la antisincronización (σn → 1) completas, es decir, en amplitud y fase. De acuerdo con el mode-lo que adoptamos, cada oscilador podrá moverse, cambiando así su posición en cada iteración siempre y cuando no alcance un valor del factor de sincronización σumbral que indica que el sistema tiende a la sincronización completa; para cuyo caso, los osciladores se detienen. Lo anterior puede expresarse como:
![]()
donde ∆y y ∆z son pequeños desplazamientos aleatorios en las direcciones y y z respectivamente, mismos que siguen una distribución Gaussiana. Como se indicó anteriormente, en el caso de dos osciladores con acoplamiento constante; el movimiento y por consiguiente, el cambio de posiciones de los mismos es irrelevante, por lo que el problema podría ser considerado como si el sistema fuese estático. Sin embargo, cuando los osciladores cambian su valor de acoplamiento en función de la distancia entre los mismos, las posiciones juegan un rol preponderante y además se debe garantizar que los osciladores no sufran colisiones, por lo que para esta situación se considera una otra condición:
![]()
siendo dumbral, una distancia umbral escogida de manera que garantice la no ocurrencia de colisiones entre los osciladores. Esta condición es importante puesto que de acuerdo con el esquema de acoplamiento dependiente de la distancia, una coli-sión entre osciladores implicaría un valor infinito del acoplamiento, situación que se debe evitar.
3 Resultados
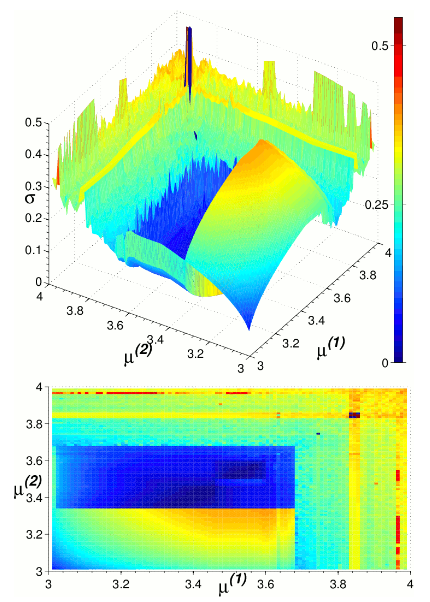
Utilizando el modelo y las condiciones descritas en §2, se caracterizó el comportamiento síncrono del sistema. Primeramente, se determina el espacio de parámetros (μ(1)−μ(2)) caracterizándolo por medio del factor de sincronización σn (Fig. 2). Los va-lores para los cuales se hacen variar los parámetros de cada oscilador corresponden a comportamientos periódicos o caóticos tal como se mostró en la Fig. 1; es decir en el intervalo [3,4].
Figure 2: (Color online) Superficie mostrando los valores del factor de sincronización σ, después de n=50000, para el espacio de parámetros (μ(1)−μ(2)) del sistema de dos mapas logísticos acoplados cuando estos presentan oscilaciones 3 ≤ μ(i) ≤ 4; siendo el valor del acoplamiento β = 0.029. En la parte inferior, se muestra la proyección en el plano (μ(1)−μ(2)), donde se puede apreciar con mayor detalle las regiones de sincronización completa que mayoritariamente se presentan para valores de los parámetros que dan lugar a comportamientos periódicos.
Sobre la base del espacio de parámetros de la Fig. 2, se escogen valores de los parámetros μ(1) y μ(2) para estudiar el comportamiento de osciladores acoplados según (2). Para ello, elegimos dos regiones para las cuales σ ≈ 0; concretamente para μ(1)=μ(2)=3.74 y μ(1)=μ(2)=3.83, las cuales co-rresponden a comportamientos de período impar.
3.1 Acoplamiento constante
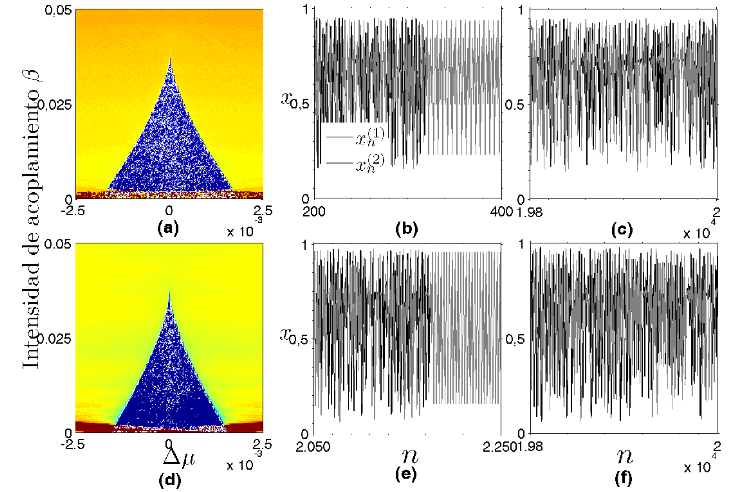
Como se mencionó en §1, existen trabajos de-dicados al estudio de la sincronización de mapas logísticos acoplados, tales como el de [181998Morgul], en el que se considera un acoplamiento de retro-alimentación y de tipo maestro-esclavo, cuyo principal resultado es que el error de sincronización decae exponencialmente y que además se tiene robustez frente a ruido; o el de [362000Taborov et al.Taborov, Maistrenko, & Mosekilde], en el cual se describe un sistema formado por tres mapas logísticos acoplados, en regimen caótico, encontrándose sincronización parcial para el sistema. Hacemos énfasis de que en el presente artículo, se estudian aspectos tales como la variación del acoplamiento con la distancia y el efecto del movimiento en la sincronización, considerando que se tiene, en todos los casos, acoplamiento mutuo y simétrico. Para caracterizar la sincronización se procede a calcular el valor de σ cuando se consideran situaciones en la que los osciladores son idénticos o difieren por un factor ∆μ y haciendo variar el valor de la intensidad de acoplamiento β (Fig. 3(a) y (d)). Se observa que para valores pequeños de β, no se tiene sincronización, y posteriormente, a partir de un valor de β ≈ 0.002 el sistema es capaz de sincronizar incluso si los osciladores son diferentes en un rango ∆μ ≈ 0.004. A medida que el acoplamiento aumenta, la región de sincronización se torna más estrecha, en contraposición a lo que normalmente ocurre con estas regiones denominadas también lenguas de Arnold, cuyo concepto está muy bien explicado en [21994Argyris et al.Argyris, Faust, & Haase]. La sincronización es posible hasta valores de β ≈ 0.0035 cuando los osciladores oscilan idénticamente. Resaltamos el hecho de que las lenguas de Arnold obtenidas, sólo consideran la situación de sincronización completa.
Figure 3: (Color online) En la parte superior, (a) Región de sincronizacíón en el plano β vs. ∆μ, representando esto último las diferencias entre los valores de los parámetros de los osciladores considerados en las regiones de la Fig. 2, donde el valor de σ→ 0 y μ(1)=μ(2)=3.74. El código de colores es similar al utilizado en la Fig. 2. Series de tiempo para (b) una situación en la que el valor β = 0.0335 conduce a la sincronización y (c) β = 0.038, donde no se presenta sincronización. En la parte inferior, (d) μ(1)=μ(2)=3.83, (e) β = 0.0365 (sincronización) y (f) β = 0.038 (comportamiento asíncrono).
3.2 Acoplamiento dependiente de la distancia
Como se vió en §3.1, la sincronización depende del valor de la intensidad de acoplamiento β; por lo que la consideración de un sistema, en el cual los osciladores pueden moverse de acuerdo a las condiciones (5)-(6), implica un cambio permanente de las posiciones de los mismos antes de que alcancen la sincronización, lo que se traduce en cambios permanentes de la intensidad de acoplamiento. Justamente, una pregunta natural es la concerniente a si el movimiento favorece o perjudica a la sincronización del sistema?, pregunta que pretende ser respondida en base a los resultados obtenidos que se muestran en la Fig. 4.
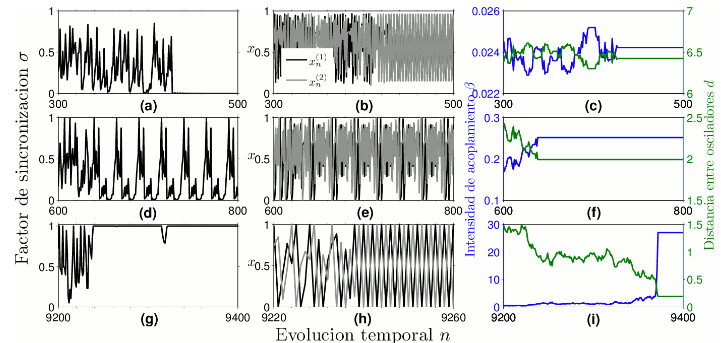
Figure 4: (Color online) Caracterización de la sincronización debida al movimiento de dos osciladores acoplados. En la parte superior se tiene sincronización completa cuando los parámetros son μ(1)=μ(2)=3.83 y las condiciones iniciales: (x0(1),y0(1),z0(1))=(0.1,5.0,5.0), (x0(2),y0(2),z0(2))=(0.25,8.3,8.756), lo que da para la distancia y la intensidad de acoplamiento iniciales: d=5.0 y β = 0.04, con la elección de una distancia umbral dumbral=2.0. Similarmente, para la fila central con los mismos valores de los parámetros de control que en la parte superior y las condiciones iniciales: (x0(1),y0(1),z0(1))=(0.1,8.0,5.0), (x0(2),y0(2),z0(2))=(0.25,8.3,8.756), lo que da para la distancia y la intensidad de acoplamiento iniciales: d=3.76829 y β = 0.07042. Finalmente para la línea inferior con μ(1)=3.83 y μ(2)=3.831 y las mismas condiciones iniciales, distancia e intensidad de acoplamiento iniciales que en la parte central, eligiendo una distancia umbral dumbral=0.2. La primera columna (a), (d) y (g) es la evolución temporal del factor de sincronización. La columna central (b), (e) y (h) es la representación de las series temporales de los osciladores en la coordenada x. La última columna (c), (f) e (i) muestran la evolución del acoplamiento y la distancia entre los osciladores.
Se encontraron tres tipos de sincronización: completa, es decir, en amplitud y fase, lo que se muestra en la Fig. 4(a)-(c), en fase (Fig. 4(d)-(f)) y en antifase, llamada también antisincronización (Fig.4(g)-(i)). Cada una de estas situaciones de sincronización tienen características bien determinadas. Así, en la sincronización completa, observamos que en el caso particular mostrado en la Fig. 4, a partir de n=427, σ ≈ 0 (Fig. 4(a)) y las señales de xn(1) y xn(2) se superponen completamente (Fig. 4(b)) con lo que se tendrá enganche tanto de amplitud como de fase; además, se ve también que de acuerdo con las condiciones impuestas, los osciladores dejan de moverse una vez que alcanzan esta sincronización (Fig. 4(c)). Una descripción más detallada de los diferentes tipos de sincronización puede encontrarse en [232001Pikovsky et al.Pikovsky, Rosenblum, & Kurths] y [252007Ramírez Ávila]. El segundo tipo de sincronización encontrado, corresponde a un enganche de fases y en este caso, σ no nos permite hacer una caracterización clara de este fenómeno, pues cuando se llega al régimen síncrono cuando n=638, el factor σ presenta un carácter oscilatorio con una periodicidad de 25 pasos de tiempo (Fig. 4(d)); en lo que concierne a las señales, a simple vista, las oscilaciones son más complicadas (Fig. 4(e)); sin embargo, procediendo al cálculo de las periodicidades (ver [82011Freire & Gallas] y [272011Ramírez Ávila & Gallas]) para ambas señales, se tiene igualmente una periodicidad de 25, coincidente con la de σ, por lo que podemos referirnos a un enganche tanto de fase como de período, mas no de amplitud (Fig. 4(e)); además, los osciladores también se detienen al alcanzar la sincronización cuando están a una distancia d=dumbral (Fig. 4(f)). Finalmente, en otra situación, cuando los osciladores son ligeramente diferentes: μ(1)=3.83 y μ(2)=3.831 y la distancia umbral es dumbral=0.2, es decir, un décimo de la usada para los anteriores casos, la sincronización se presenta para σ = 1 (Fig. 4(g)); esto significa que xn(1)+xn(2)=1, lo que equivale a que cada uno de los osciladores tiene un período 2 y que la oscilación de ambos es entre 0 y 1 (Fig. 4(h)) por lo que estos antisincronizan teniendo la misma amplitud; es interesante ver que contraria-mente a los casos anteriores, en los que una vez que los osciladores sincronizaban, estos se detenían, en este caso los osciladores continúan moviéndose estando sincronizados durante 133 pasos de tiempo hasta que para n=9372, ellos se detienen (Fig. 4(i)).
Basados en estos resultados, podemos responder a la pregunta planteada al principio, indicando que el movimiento tiende a favorecer la sincronización del sistema puesto que estudiando situaciones iniciales para las cuales no es posible la sincronización, el movimiento de los osciladores, permite alcanzar la sincronía. Por supuesto, una respuesta más completa podría ser dada en base a estudios que contemplen espacios muestrales mayores.
4 Conclusiones y perspectivas
La caracterización de la sincronización completa de un sistema de dos mapas logísticos acoplados nos permitió seleccionar los parámetros de control que dan lugar a comportamiento síncrono. Utilizando estos valores de los parámetros de control, se encontró que el movimiento de los osciladores permite la sincronización, incluso si las condiciones iniciales a nivel de acoplamiento (distancia) no permitiesen este comportamiento para un sistema estático; es decir, el movimiento con las condiciones impuestas para el mismo, permiten al sistema encontrar el atractor que da lugar a comportamiento síncrono. Por otra parte, se encontraron diferentes tipos de sincronización aparte de la completa, por lo que para posteriores estudios se prevé buscar otros caracterizadores de la sincronización que tengan en cuenta tanto la sincronización en amplitud como también la correspondiente en fase para así poder estudiar también sistemas caóticos. Otro aspecto importante para futuros trabajos es el concerniente al transiente caótico, estudiado en [62006Buszko & Stefanski], que se tiene antes de alcanzar la sincronización; el conocimiento y caracterización adecuada de este transiente es de gran importancia para conocer la dinámica del sistema. Posibles aplicaciones de este tipo de sistemas están en relación con sistemas tanto naturales como artificiales. Así, varios sistemas biológicos oscilatorios tales como las luciérnagas macho, que utilizan sus señales luminosas síncronas para obtener una respuesta de las hembras con fines relacionados a la reproducción, fenómeno que fue denominado principio de respuesta a la sincronización y estudiado por [262011Ramírez Ávila et al.Ramírez Ávila, Deneubourg, Guisset, Wessel, & Kurths], implican el movimiento de los insectos y la influencia del mismo tanto en la sincronización como en la respuesta es una aplicación potencial de este trabajo. La sincronización de objetos móviles tales como robots, es también importante sobre todo cuando se pretende que los mismos ejecuten cierta tarea. La continuación natural de este trabajo es el estudio de sistemas compuestos por muchos osciladores y que eventualmente forman una red, en la cual, el movimiento de los nodos de la red podría optimizar la transmisión de cierta información. Finalmente, la forma de las lenguas de Arnold obtenidas, sugiere que se pueden buscar esquemas de acoplamiento más adecuados, uno de los cuales podría ser del tipo de potencial repulsivo como por ejemplo V(r)\thicksim (κ/r)n, con n=9−16 y donde κ representa el alcance efectivo de la repulsión; o con potenciales tipo Lennard-Jones para tener inte-racciones atractivas a largas distancias y repulsivas a cortas distancias, aspecto que estaría ligado también a la dinámica de movimiento espacial de los osciladores.
G.M.R.A. agradece a A. García Cantú por las motivantes discusiones respecto a elementos móviles y al Referee que con sus sugerencias ayudó a mejorar el presente trabajo.
References
1.- Aihara I. (2009), Phys. Rev. E 80, 011918 [ Links ]
[21994Argyris et al.Argyris, Faust, & Haase]
2.- Argyris J., Faust G. & Haase M. (1994), An exploration to chaos (Amsterdam: Elsevier Science B.V.) [ Links ]
[32009Batista et al.Batista, Batista, de Pontes, Lopes, & Viana]
3.- Batista C. A. S., Batista A. M., de Pontes J. C. A., Lopes S. R. & Viana R. L. (2009), Chaos Soliton. Fract. 41, 2220 [ Links ]
4.- Buck J. & Buck E. (1976), Sci. Am. 234, 74 [ Links ]
5.- Buck J. B. (1935), Science 81, 339 [ Links ]
6.- Buszko K. & Stefanski K. (2006), Chaos Soliton. Fract. 27, 630 [ Links ]
7.- Czirok A. & Vicsek T. (2000), Physica A 281, 17 [ Links ]
8.- Freire J. G. & Gallas J. A. C. (2011), Physical Chemistry Chemical Physics 13, 12191 [ Links ]
[92011García Cantú Ros et al.García Cantú Ros, Antonopoulos, & Basios]
9.- García Cantú Ros A., Antonopoulos C. G. & Basios V. (2011) Chaos Soliton. Fract. 44, 574 [ Links ]
10.- Greenfield M. & Roizen I. (1993), Nature 364, 618 [ Links ]
11.- Grinstein G. & Linsker R. (2005), P. Natl. Acad. Sci. USA 102, 9948 [ Links ]
[121971Hanson et al.Hanson, Case, Buck, & Buck]
12.- Hanson F. E., Case J. F., Buck E. & Buck J. (1971), Science 174, 161 [ Links ]
13.- Janson N. B. (2012), Contemp. Phys. 53, 137 [ Links ]
[142008Landau et al.Landau, Páez, & Bordeianu]
14.- Landau R., Páez M. & Bordeianu C. (2008), A survey of computational physics: introductory computational science (Princeton: Princeton University Press) [ Links ]
15.- Lin F.-Y. & Tsai M.-C. (2007), Opt. Express 15, 302 [ Links ]
[162009López-Gutiérrez et al.López-Gutiérrez, Posadas-Castillo, López-Mancilla, & Cruz-Hernández]
16.- López-Gutiérrez R. M., Posadas-Castillo C., López-Mancilla D. & Cruz-Hernández C. (2009), Chaos Soliton. Fract. 42, 277 [ Links ]
17.- May R. M. (1976), Nature 261, 459 [ Links ]
18.- Morgul O. (1998), Phys. Lett. A 247, 391 [ Links ]
19.- Murray J. (2002), Mathematical Biology I: An Introduction (Berlin: Springer) [ Links ]
[202008Nowotny et al.Nowotny, Huerta, & Rabinovich]
20.- Nowotny T., Huerta R. & Rabinovich M. I. (2008), Chaos 18, 037119 [ Links ]
21.- Pérez G. & Cerdeira H. A. (1995), Phys. Rev. Lett. 74, 1970 [ Links ]
22.- Pikovsky A. & Maistrenko Y. (2003), NATO Science Series II. Mathematics, Physics and Chemistry, Vol. 109, Synchronization: Theory and Application (Dordrecht: Kluwer Academic Publishers) [ Links ]
[232001Pikovsky et al.Pikovsky, Rosenblum, & Kurths]
23.- Pikovsky A., Rosenblum M. & Kurths J. (2001), Cambridge nonlinear science series, Vol. 12, Synchronization : a universal concept in nonlinear sciences (New York: Cambridge University Press) [ Links ]
23.- Ramírez Ávila G. M. (2004), PhD thesis [ Links ]
24.- -. (2007), Revista Boliviana de Educación Superior en Ciencias 7, 25 [ Links ]
[262011Ramírez Ávila et al.Ramírez Ávila, Deneubourg, Guisset, Wessel, & Kurths]
25.- Ramírez Ávila G. M., Deneubourg J. L., Guisset J. L., Wessel N. & Kurths J. (2011), Europhys. Lett. 94, 60007 [ Links ]
[272011Ramírez Ávila & Gallas]
26.- Ramírez Ávila G. M. & Gallas J. A. C. (2011), Revista Boliviana de Física 19, 1 [ Links ]
[282003Ramírez Ávila et al.Ramírez Ávila, Guisset, & Deneubourg]
27.- Ramírez Ávila G. M., Guisset J. L. & Deneubourg J. L. (2003), Physica D 182, 254 [ Links ]
29.- Rasband S. (1990), Chaotic dynamics of nonlinear systems (Wiley) [ Links ]
30.- Saha P. & Strogatz S. H. (1995), Math. Mag. 68, 42 [ Links ]
31.- Sarkar S. (2010), Chaos 20, 043108 [ Links ]
32.- Shibata T. & Kaneko K. (2003), Physica D 181, 197 [ Links ]
[331996Shimoyama et al.Shimoyama, Sugawara, Mizuguchi, Hayakawa, & Sano]
33.- Shimoyama N., Sugawara K., Mizuguchi T., Hayakawa Y. & Sano M. (1996), Phys. Rev. Lett. 76, 3870â [ Links ]
34.- Sismondo E. (1990), Science 249, 55 [ Links ]
35.- Sueur J. (2002), Science et Avenir 50 [ Links ]
[362000Taborov et al.Taborov, Maistrenko, & Mosekilde]
36.- Taborov A. V., Maistrenko Y. L. & Mosekilde E. (2000), Int. J. of Bifurcat. Chaos 10, 1051 [ Links ]
37- Verhulst P. (1838), Corresp. Math. Phys. 10, 113 [ Links ]
39.- Wei D. Q. & Luo X. S. (2007), Europhys. Lett. 78, 68004 [ Links ]
40.- Yang T. & Chua L. O. (1996), IEEE T. Circuits-I 43, 817 [ Links ]
[401997Yang et al.Yang, Wu, & Chua]
41.- Yang T., Wu C. W. & Chua L. O. (1997), IEEE T. Circuits-I 44, 469 [ Links ]
42.- Zanette D. H. & Mikhailov A. S. (2004), Physica D 194, 203 [ Links ]
File translated from TEX by TTH, version 3.89.
On 15 Jun 2013, 23:29.