MODELO GEOMÉTRICO Y CARACTERIZACIÓN ESPECTRAL DE TUBOS FLUORESCENTES DE LUZ ULTRAVIOLETA

GEOMETRICAL MODEL AND SPECTRAL CHARACTERIZATION OF FLUORESCENT TUBES EMITTING ULTRAVIOLET LIGHT

 

EMILIANA JUANIQUINA, FRANCESCO ZARATTI, FLAVIO GHEZZI, FERNANDO VELARDE, & A. R. TICONA BUSTILLOSt

Laboratorio de Física de la Atmósfera
Instituto de Investigaciones Físicas, Carrera de Física
Universidad Mayor de San Andrés
c. 27 Cota-Cota, Campus Universitario, Casilla de Correos 8639
La Paz — Bolivia

 

---

RESUMEN

La radiación de las lámparas ultravioleta, del tipo usado en las camas solares de centros de belleza, es medida y caracterizada usando técnicas espectrales y métodos de dosimetría. Se observa la presencia significativa de radiación ultravioleta B, la cual representa un peligro en su uso en el caso de no tener un control en el tiempo de exposición. Usando el principio de superposición se desarrolla un modelo computacional que toma en cuenta los datos medidos y nos permite calcular el efecto combinado de varias lámparas según la geometría en la que dichas lámparas están dispuestas.

Descriptores: Evaluación de dosimetría/exposición (radiación UV) — simulación computa­cional (en física médica)

Código(s) PACS: 87.50.up, 87.64.Aa

ABSTRACT

The radiation from ultraviolet lamps, of the type used in sun beds, is measured and char­acterised using spectral and dosimetric techniques. We observe the significant presence of ultraviolet B radiation which represents a danger to health if time exposure is uncontrolled. Using the superposition principle we developed a computational model which takes the mea­sured radiation data of one lamp and calculates the combined effect of many lamps and geometries that make up potential systems such as sun beds.

Subject headings: Dosimetry/exposure assessment of UV radiation — Computer simulation (in medical physics)

---

1. INTRODUCCIÓN

Hoy en día existen en Bolivia muchos sectores e industrias que usan fuentes artificiales de luz Ul­tra Violeta (UV), por ejemplo soldadores, radiólogos, las curtiembres, etc. A pesar de esto, nuestro país no dispone de una ley relacionada al uso de dichas fuentes. Por eso es esencial realizar un análisis es­pectral y de dosis de las fuentes de radiación UV que nos permita regular su uso (Camacho 2001;Zulu­aga 2009). Uno de las mayores aplicaciones de la ra­diación UV está en la fabricación de camas y duchas solares.

Las camas solares nos brindan una forma contro­lada de radiación, mediante la cual podemos bron­cear nuestra piel, a diferencia de la radiación solar que presenta prácticamente todo el espectro de e­nergías. Sin embargo, el mal uso en los tiempos de

t aticona@fiumsa.edu.bo

exposición podría resultar en un daño, si no tomamos en cuenta algunos factores que caracterizan a la ra­diación emitida por estas, así como la interacción de dicha radiación con nuestra piel (Martin et al. 1999).

El principal efecto de bronceado en la piel es pro­ducido por la radiación Ultra Violeta A (UVA), por lo cual las lámparas usadas solo deberían emitir este tipo de radiación. Lamentablemente una lámpara que solo emita este tipo de radiación es simplemente un modelo idealizado, ya que debido a diferentes cir­cunstancias técnicas, es imposible que solo se pro­duzca un solo tipo de radiación de manera contro­lada, por lo que podemos encontrar otros tipos de ra­diación como la Ultra Violeta B (UVB), la cual puede ser muy nociva para nuestra piel ya que produce diferentes daños en ésta (Miyamura et al. 2011).

Por otro lado, la presencia de radiación UVB en la emisión de estas lámparas, las hacen muy útiles para otras aplicaciones como en biología y ciencias de

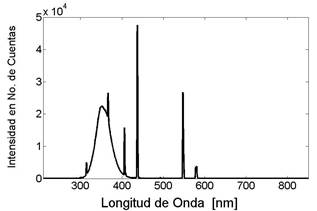
FIG. 1.- Espectro de una lámpara mostrando su intensidad en número de cuentas, en función a las longitudes de onda, medido por un espectro fotómetro Ocean Optics, en la parte central de la lámpara a 20 cm de su eje.

materiales; por ejemplo se han usado para simular en forma controlada condiciones externas en el estu­dio de resistencia de materiales o para observar dife­rentes cambios en el comportamiento de las plantas (Palenque et al. 2011).

En este trabajo presentamos un estudio de la ra­diación que caracteriza a las lámparas que son u­sadas en este tipo de camas en el mercado local. Estudiamos el espectro y la dosis de una de estas lámparas en función a la distancia radial a su eje, mostrando la cantidad relativa de las componentes en la radiación emitida por dicho tipo de lámparas.

Usando el principio de superposición, proponemos un modelo que nos permita calcular el efecto combi­nado de varias lámparas según la geometría en las que se encuentran dispuestas. Esto nos permite in­dicar la dosis y los tiempos máximos de exposición recomendables que corresponden a cada tipo de cama o ducha solar (Teikari 2007).

2. ESPECTRO Y DOSIS DE UNA LÁMPARA

Para estudiar el espectro de estas lámparas u­samos en primera instancia un espectro fotómetro Ocean Optics USB 4000, el cual recibe luz a través de una fibra óptica. Este instrumento mide de 180 nm hasta a 900 nm, acumulando los datos en número de cuentas por canal, con un espacio de aproxi­madamente 0.2 nm entre canales, correspondientes a las longitudes de onda medidas. Esto nos permi­tiría eventualmente analizar el espectro correspon­diente al Ultra Violeta (UV), visible y parte del In­fra Rojo (IR). Las limitaciones de la fibra óptica cortan esta información desde aproximadamente el UVB, hasta parte del IR. Además, el uso de la fibra óptica presenta algunas restricciones geométricas, en primera lugar, el ángulos sólido de detección de una fibra cubre un espacio relativamente pequeño, lo cual limita sus datos (Martín et al. 1999); en segundo lugar, cada vez que realizamos una medida con este instrumento, debemos situarlo de manera perpendi­cular a la fuente que estamos midiendo, lo cual no es técnicamente sencillo, de otra manera por la res­tricción mencionada antes, los datos medidos serán

TABLA 1

DIVISIÓN DEL ESPECTRO ELECTROMAGNÉTICO, EN FUNCIÓN A
LA LONGITUD DE ONDA.

menores a los reales. Los datos obtenidos con este detector fueron comparados con los obtenidos por un espectro fotómetro Newport (OrielCat 78347), con el cual se obtuvieron los mismos resultados.

En la última década, la tecnología ha desarrollado dosímetros de UVA y UVB muy estables y de precios asequibles (Martín et al. 1999;Godar 2005). En se­gunda instancia medimos la dosis de estas lámparas usando un dosímetro Gigaherts OptikXD-9501-4, cuyo cabezal contiene dos sensores que pueden medir la UVA y UVB simultáneamente. Dicho cabezal es plano y situado en el propio instrumento, esto facilita mucho su uso, ya que su ángulo sólido de detección es muy amplio y su colocación, en forma perpendicular con respecto a la fuente, es relativamente sencilla.

Una de las lámparas de bronceado artificial más comunes y usadas en el mercado boliviano por los sa­lones de belleza es la Wolff Velocity de 80 W de po­tencia, con 3.80 cm de diámetro y 150 cm de longitud.

Para realizar las medidas, se sitúa la lámpara hor­izontalmente en una mesa óptica, en un ambiente obscurecido, con paredes negras y con muy poca re­flexión, así realizamos las medidas sobre el eje radial de la lámpara, con ambos detectores.

La figura 1 muestra el espectro que es obtenido por el espectro fotómetro Ocean Optics al medir la radiación de una de estas lámparas solares. Pode­mos observar la región del espectro que tiene mayor intensidad, así como también algunos picos carac­terísticos de estas lámparas debido al gas que usan éstas y el revestimiento del tubo.

Para el estudio del espectro se usan protoco­los bien establecidos (EUROPEAN-COMMISSION 2005;IEC-1228 1996;Gerber et al. 2002). En la Tabla 1 podemos observar la división del espectro electro­magnético, en función a la longitud de onda.

En la figura 2 podemos observar un estudio com­parativo del espectro de la figura 1 y el ruido de fondo obtenido bajo las mismas condiciones de medida del caso anterior, pero con la lámpara apagada. Para no­tar mejor las diferencias, en esta figura mostramos el logaritmo natural de la intensidad.

Observamos que cuando la lámpara es encendida se notan cambios desde aproximadamente los 280 nm hasta los 700 nm, esto implica que su espectro se extiende desde la radiación UVB hasta parte del visible, siendo mucho más intensa en la parte del UVA, como era de esperarse en este tipo de lámparas. La contribución de radiación Infra Roja (IR) solo se nota en los datos de los puntos muy cercanos a los extremos, donde se encuentran los bornes eléctricos, pero esto no corresponde a la radiación emitida por la lámpara, por esta razón no tomaremos en cuenta esta parte del espectro en nuestro análisis.

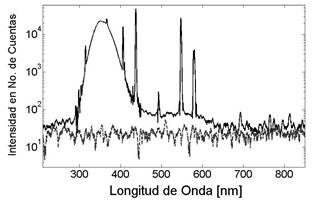
FIG. 2.— Espectro de una lámpara mostrando el logaritmo de su intensidad en número de cuentas, junto a la radiación de fondo medida bajo las mismas condiciones de la figura 1.

Una vez que tenemos diferenciadas las bandas del espectro que nos interesan en el presente es­tudio, podemos caracterizar su contribución en la emisión de estas lámparas. Un importante resultado es obtenido al estudiar la radiación en función a la distancia. En la figura 3 podemos observar el com­portamiento de las componentes UVA y UVB con re­specto a la lámpara, medidas sobre el eje radial de dicha lámpara, en su parte central.

El mismo análisis puede ser realizado con el dosímetro, este comportamiento puede ser observado en la figura 4, donde se muestra el comportamiento de la dosis en función a la distancia.

Para tener una idea de los datos obtenidos con el dosímetro, presentamos dos ejemplos:

1.    La dosis del sol a medio día tiene una dosis de 45.7 W/m2 para UVA y 1 W/m2 para UVB, esto a una altura 2750 m sobre el nivel del mar en un día completamente soleado de octubre (29/10/2009).

2.    Una ducha solar moderna de 5 tubos (cada uno de 160 W) al nivel de la piel (30 cm) es de 194 W/m2 de UVA y 2.1 W/m2 de UVB (Soria 2010).

En la figuras 3 y 4 podemos observar que el com­portamiento de la radiación con respecto a la distan­cia obedece, en su mayor parte, una ley de poten­cia con exponente —1, para los cuatro casos mostra­dos en estas figuras. Esto corresponde al compor­tamiento de la intensidad de la radiación emitida por un hilo cargado infinito. En el caso de la lámpara este comportamiento se debe a dos factores, primero, como habíamos mencionado, el ángulo sólido de de­tección de estos detectores son restringidos, lo cual hace que no puedan observar la lámpara entera, en­tonces desde el punto de vista de estos detectores la lámpara es infinita; en segundo lugar, como el diámetro de la lámpara es relativamente pequeño, a cierta distancia se asemeja a un hilo muy delgado. A distancias pequeñas de la lámpara si se nota el volu­men real de ésta, lo cual hace que el comportamiento descrito anteriormente ya no sea válido.

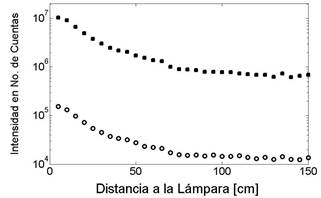
FIG. 3.— Comportamiento de la intensidad de la radiación, me­dida con respecto a la distancia sobre el eje radial (centro de la lámpara). Los cuadrados (parte superior) corresponden a ra­diación UVA y los círculos (parte inferior) a la radiación UVB.

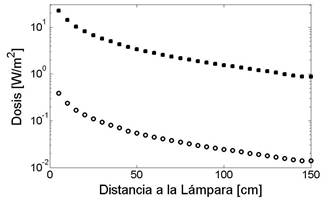
FIG. 4.— Comportamiento de la dosis de la radiación, medida con respecto a la distancia sobre el eje radial (centro de la lámpara). Los cuadrados (parte superior) corresponden a radiación UVA y los círculos (parte inferior) a la radiación UVB.

Por su parte la componente visible de la lámpara también presenta el mismo comportamiento.

Considerando que estos comportamientos son si­milares podemos determinar un factor de conversión entre los datos de ambos equipos, con lo cual tenemos todos los resultados en unidades de W/m2. El factor obtenido al comparar los puntos de ambas figuras es de (5.12 ± 0.09) x 105. La mayor contribución al error en la determinación de este factor, se debe a los datos obtenidos con la fibra óptica, como se observa en la figura 3. Como habíamos mencionado existe mucha dificultad técnica al acomodar la fibra en forma per­pendicular a la lámpara.

3. ESPECTRO DE ACCIÓN

El efecto de la radiación electromagnética sobre la piel es más nocivo para altas energías, este efecto está cuantificado en el llamado espectro de acción. Existen diferentes definiciones para este espectro de acción, nosotros usamos la definición SIE que nos da un índice dado por (IEC-1228 1996):

Donde I representa la intensidad de la radiación,

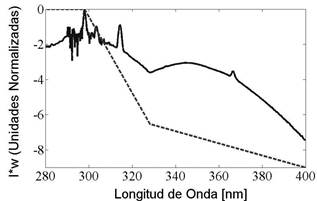
FIG. 5.— Comportamiento de I(A) •w (A). La línea punteada toma I = 1. La línea continua toma los valores de I medidos para la lámpara, los cuales fueron mostrados en la figura 1, estos se en­cuentran normalizados para una fácil comparación. El resultado se muestra en escala logarítmica.

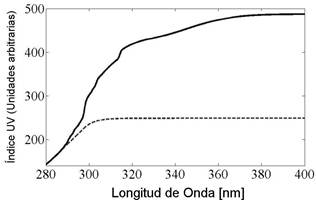
FIG. 6.— Índice UV (espectro de acción, definición SIE). La línea punteada toma I=1. La línea continua toma los valores de I medi­dos para la lámpara. Las unidades son arbitrarias para una fácil comparación.

A la longitud de onda y w es la ponderación del efecto de la radiación en función a su longitud de onda; dada por:

En la figura 5 graficamos el comportamiento de I(λ) • w(λ), primero tomamos el valor de I = 1 y comparamos este resultado con el obtenido para la lámpara, considerando las intensidades de la figura 1, para poder comparar estos resulta­dos, normalizamos los resultados obtenidos para la lámpara. Para tener una mejor idea de este resul­tado mostramos el logaritmos natural de I(λ) • w(λ).

Como podemos observar en la figura 5, la con­tribución de radiación nociva es bastante impor­tante en la radiación emitida por estas lámparas. Lamentablemente, las restricciones de la fibra óptica solo nos permiten apreciar medidas a partir de aproximadamente 290 nm, esto no significa que la lámpara no emita radiación con longitudes de onda

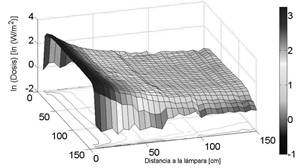
FIG. 7.— Dosis medida de la radiación emitida por la lámpara (en escala logarítmica), en función a la distancia de la lámpara y al eje paralelo a la lámpara. (Figura a color online).

inferiores, lo cual incrementa aun mas, el riesgo en el uso no controlado de estas lámparas.

En la figura 6 observamos el índice UV calculado para la lámpara, usando las ecuaciones 1 y 2, para comparación se muestra el índice considerando la in­tensidad igual a 1, las unidades son arbitrarias, para que pueda compararse los comportamientos. A pesar que para ambas curvas comienzan en el mismo valor para 280 nm (esto debido a la manipulación inten­cional de las unidades), se nota claramente, que la radiación UVB tiene una contribución bastante im­portante, lo cual demuestra nuevamente lo peligroso que podría resultar el uso de estas lámparas, como habíamos mencionado antes.

4. DEPENDENCIA DE LA RADIACIÓN CON LA DISTANCIA

Para poder estudiar los posibles impactos de este tipo de lámparas sobre un cuerpo dentro de una cama solar, estudiamos el comportamiento de la in­tensidad de la radiación emitida en función a la dis­tancia.

Tomamos medidas a lo largo de un eje paralelo al eje radial de la lámpara con espacios de 5 cm entre cada medida. Comenzamos a una distancia de 5 cm de la lámpara y luego repetimos este procedimiento a cada 5 cm hasta alcanzar los 150 cm de distancia al tubo. Esto nos permite estudiar las distancias im­portantes de uso de estas lámparas, ya que en una cama solar, la persona no se encuentra a una distan­cia mayor a las mencionadas.

En la figura 7 observamos la intensidad de la radiación total de la lámpara medida a diferentes distancias, mostradas en el eje horizontal de la izquierda (profundidad en la figura); en el eje hori­zontal de la derecha tenemos las distancias parale­las a la lámpara medida en centímetros. El eje verti­cal y las diferencias de colores nos muestran la do­sis de la radiación, la cual fue obtenida usando el factor de corrección entre cuentas y dosis, calculado en la segunda parte de este trabajo. Para que pueda apreciarse con mayor claridad la mostramos en es­cala logarítmica. Vale la pena recalcar que para esta figura solo usamos las contribuciones de UVB, UVA y visible, por lo explicado con anterioridad, con res­pecto a la sensibilidad de la fibra óptica.

Como podíamos esperar, la intensidad se reduce aproximadamente 20 veces, desde los 5 cm hasta los

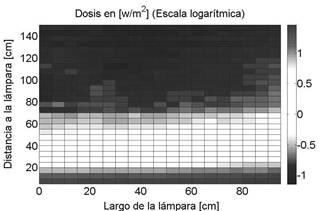
FIG. 8.— Dosis medida de la radiación visible emitida por la lámpara (en escala logarítmica), en función a la distancia de la lámpara y al eje paralelo a la lámpara. (Figura a color online).

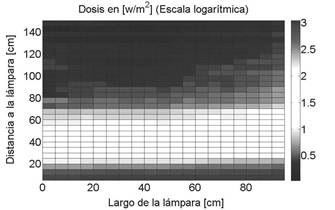
FIG. 9.— Dosis medida de la radiación UVA emitida por la lámpara (en escala logarítmica), en función a la distancia de la lámpara y al eje paralelo a la lámpara. (Figura a color online).

150 cm de distancia hacia la lámpara. La sensibili­dad del espectro fotómetro, nos permite observar al­gunas irregularidades en los extremos de la figura, debido a algunos reflejos en las paredes.

Para el resto de nuestro análisis consideramos solo la parte más intensa de la lámpara, que corresponde a los 100 centímetros centrales. Como se puede apre­ciar en la figura 7, en los extremos, es decir 25 cm de cada extremo, los efectos de borde hacen que la inten­sidad de la radiación emitida sea menor, dándonos valores menores a los que serán mostrados a conti­nuación.

Podemos analizar por separado las contribuciones importantes del espectro de la lámpara y estudiar su comportamiento en función a la distancia. En la figura 8 analizamos el comportamiento de la parte visible del espectro de la lámpara.

El comportamiento es el esperado, mostrando prácticamente el mismo patrón que la figura de la in­tensidad total. De igual manera podemos analizar la contribución de la radiación UVA, en función a la dis­tancia en la figura 9. El comportamiento es el mismo que el observado en las figuras 7 y 8.

Finalmente podemos realizar el mismo tipo de análisis con la componente UVB, la cual, como ya

TABLA 2

PORCENTAJE PROMEDIO DE CADA TIPO DE RADIACIÓN.

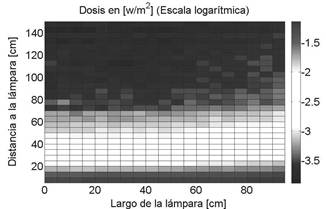
FIG. 10.— Dosis medida de la radiación UVB emitida por la lámpara (en escala logarítmica), en función a la distancia de la lámpara y al eje paralelo a la lámpara. (Figura a color online).

habíamos mencionado, presenta un efecto nocivo para la piel. En la figura 10 observamos la intensidad de esta radiación en función a la distancia al tubo. Como podemos observar, la contribución de esta ra­diación no es despreciable.

Podemos obtener el porcentaje de cada una de es­tas tres contribuciones para cada punto donde rea­lizamos la medición, este porcentaje es aproximada­mente constante para todos los puntos donde se rea­lizaron estas medidas, los valores son mostrados en la tabla 2.

5. MODELO GEOMÉTRICO

En una cama o en una ducha solar, se tiene un a­rreglo de varias lámparas actuando al mismo tiempo. Debido a las dificultades mencionadas antes, con res­pecto a las restricciones geométricas que tienen los sensores lo cual ya fue reportado por Martin et al. (1999), resulta muy difícil realizar una medida del efecto combinado de todas estas lámparas.

Una vez que tenemos datos medidos para una lámpara, podemos usar el principio de superposición para poder determinar el efecto combinado de varias lámparas. Nuestro modelo parte de un determinado arreglo de lámparas, para lo cual necesitamos las posiciones de cada lámpara y además podemos con­siderar la intensidad de cada lámpara. Ya que te­nemos caracterizado todo el espectro y el compor­tamiento de la intensidad de la radiación en función de la distancia, prácticamente para cualquier punto cercano a la lámpara, ahora resulta muy sencillo re­hacer un mapeo completo del comportamiento para cualquier intensidad medida en cualquiera de estos puntos.

 

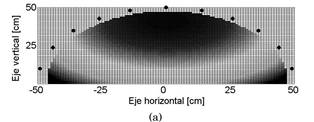
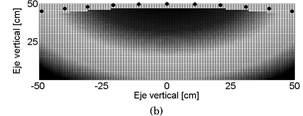
FIG. 11.- Corte transversal de una determinada distribución de lámparas (tipo cama solar). Se muestra la intensidad de la ra­diación en función a la posición. (a) Distribución cerrada. (b) Dis­tribución abierta. (Figura a color online).

Una vez que se tienen caracterizadas las lámparas, podemos considerar cualquier punto cercano a es­tas y calcular cual es la intensidad de radiación que este punto está recibiendo de la configuración de lámparas. De esta manera podemos calcular el tiempo de exposición que se requiere, según el ob­jetivo para el cual se utiliza una determinada confi­guración.

En la figura 11 mostramos un barrido completo para posiciones cercanas a dos determinados arre­glos geométricos de lámparas, tipo camas solares. Realizamos un corte transversal en la posición cen­tral de las lámparas donde, como habíamos men­cionado, se tiene una mayor intensidad de radiación.

En la figura 11(a) se muestra un arreglo bastante cerrado lo cual hace que la intensidad de radiación, sea demasiado alta casi en todos los puntos cer­canos a esta configuración, además notamos una dis­tribución poco homogénea, lo cual representaría un peligro en una cama solar, ya que ciertos puntos quedan más expuestos que otros, lo cual daría como resultado un bronceado no uniforme. Por su parte los resultados mostrados en la figura 11(b) correspon­den a una configuración menos cerrada, lo cual da una distribución de la radiación, menos localizada y a una distancia de uso típica en una cama solar, pre­sentaría un bronceado más uniforme.

6. CONCLUSIONES Y PERSPECTIVAS

La razón del uso de una cama solar, es obtener un bronceado rápido y controlado. Podemos observar en las figuras 1 y 2 así como también en la tabla 2, que existe una pequeña contribución de radiación UVB, en la radiación emitida por estas lámparas. Debido al tipo de daño que se puede producir con este tipo de radiación, aún esta pequeña contribución, es muy importante en comparación al resto de la radiación UVA, como mostramos en las figura 5 y 6.

Está claro que este tipo de lámparas son muy efi­cientes en la emisión de radiación UVA, por lo tanto son muy eficientes en el bronceado, como pudimos observarlo en las figura 9, de todos modos, se debe tener cuidado con el tipo de lámparas, controlando los tiempos de exposición en base al espectro de acción de estas.

El modelo presentado en este trabajo, también puede ser usado para el control en el tiempo de ex­posición, ya que nos da en forma sencilla una buena aproximación, a la intensidad total a la que una per­sona está expuesta en este tipo de camas. Además podemos usar este mismo modelo para otro tipo de aplicaciones, por ejemplo en muchos casos se usan estas mismas lámparas, para simular en laboratorio el comportamiento de plantas o animales expuestos a este tipo de radiación. Entonces podemos deter­minar una configuración más eficiente para una de­terminada aplicación. Es sencillo, con el uso de este modelo, simular sectores menos expuestos, debido a sombras u obstáculos que se presentan en un deter­minado ambiente, así tenemos control de cuanta ra­diación recibe cada porción de un determinado ob­jeto.

Finalmente podemos decir que el método y modelo desarrollado en este trabajo se puede aplicar a otras fuentes artificiales usadas en otras industrias.

AGRADECIMIENTOS

Ma. Lourdes Soria M. y su centro de belleza Svelta Cochabamba por su ayuda e interés en un bronceado artificial saludable.

Eduardo Palenque por sus comentarios y observa­ciones sobre este trabajo.

 

REFERENCIAS

1 Camacho F. (2001), Revista internacional de dermatología y dermo cosmética, 4 (7), 441        [ Links ]

2 EUROPEAN-COMMISSION (2005), Opinion on Biological effects of ultraviolet radiation relevant to health with particular refer­ence to sun beds for cosmetic purposes (SCCP/0949/05)        [ Links ]

3 Gerber B., Matiz P., Moser M., Bressoud D. & Braun-Fahrlander C. (2002), Photochemistry and Photobiology, 76 (6), 664        [ Links ]

4 Godar D. E. (2005), Photochemistry and Photobiology, 81, 736        [ Links ]

5 IEC-1228 (1996), amendment 1        [ Links ]

6 Martin C. J., Currie G. D. & Pye S. D. (1999), Phys. Med. Biol. , 44, 843        [ Links ]

7 Miyamura Y. & et al. (2011), Pigment Cell Melanoma Res., 24 (1), 136        [ Links ]

8 Palenque E. R., Ghezzi F. & Vargas C. (2011), Revista Bolviana de Física, 18, 17        [ Links ]

9 Soria M. L. (2010), Centro de belleza Suelta Cochabamba

10 Teikari P. (2007), Light Pollution (Universitat Técnica Catalunya) 11 Zuluaga A. (2009), Rey. Asoc. Colomb. Dermatol. , 17, 205         [ Links ]         [ Links ]

 

 

Recibido 1 de Marzo de 2011;

aceptado 9 de Julio de 2012