Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista Boliviana de Física
On-line version ISSN 1562-3823
Revista Boliviana de Física vol.19 no.19 La Paz 2011
SIMULACIÓN DEL PROBLEMA DE N CUERPOS CARGADOS: EL ÁTOMO CLÁSICO
SIMULATION OF THE N CHARGED BODIES PROBLEM: THE CLASSICAL ATOM
V. M. Peñafielf
Instituto de Investigaciones Físicas, Carrera de Física
Universidad Mayor de San Andrés
c. 27 Cota-Cota, Campus Universitario, Casilla de Correos 8639
La Paz - Bolivia
Resumen
Un conjunto de rutinas computacionales, diseñado para calcular y visualizar -en tiempo real- las trayectorias de N cuerpos cargados y urgidos, en consecuencia, por fuerzas electromagnéticas de tipo Coulomb-Abraham-Lorentz, ha sido empleado en la solución explícita y completa de la ecuación de movimiento del "átomo clásico". El código encargado de evaluar el efecto de tales interacciones es de particular interés, obviamente, por contener el término de radiación por desaceleración, proporcional a la derivada temporal de la aceleración y sujeto de recelo por su difícil tratamiento analítico e interpretación. Los resultados permiten representar gráficamente las trayectorias y obtener una estamación razonable del "tiempo de colapso" de este sistema.
Descriptores: radiación de cargas en movimiento - técnicas computacionales y simulaciones - electrodinámica clásica
Código(s) PACS: 41.60.-m, 02.70.-c, 03.50.De
Abstract
A set of computational routines has been employed for calculating in real time the trajectories of N charged bodies which are acted upon by electromagnetic forces of the Coulomb-Abraham-Lorentz type. These routines yield the complete solution of the motion equation for the "classical atom". The computer code that evaluates the interaction effect is interesting in itself because it contains the radiation damping term, which is proportional to the time-derivative of the acceleration; this is often a cumbersome analytical and interpretational task. The results permit the graphical representation of the trajectories and, a reasonable estimate of the "collapse time".
Subject headings: radiation by moving charges - computational techniques and simulations - classical electrodynamics
INTRODUCCIÓN
La capacidad de los computadores actuales permite ya cierta sofisticación en el cálculo y despliegue gráfico de sistemas complejos, como el problema de N cuerpos eléctricamente cargados, el cual puede ser simulado en tiempo real para un apreciable número de componentes. Se ha diseñado, al efecto, una serie de rutinas (ensamble 32) de las cuales, en el presente trabajo, interesa sólo la que evalúa las ecuaciones de movimiento; aplicándola al caso de dos partículas con cargas y masas propias del protón y el electrón, sistema conocido en la literatura como el "átomo clásico".
Un procedimiento rápido (y obvio) de estimar el tiempo que tardaría un electrón en caer sobre el protón en un átomo, clásicamente tratado, es el de recurrir a la fórmula de Larmor para un dipolo rotatorio
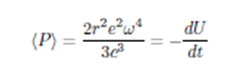
y combinarla con las variables obtenidas para una trayectoria circular:
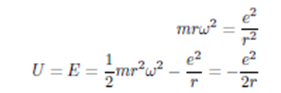
para obtener, con r0 = e2/mc2 (radio clásico del electrón),
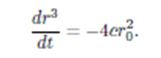
Integrada ésta desde rB (radio de Bohr), para t=0, hasta 0 para t=tcolapso, queda, usando las magnitudes usuales,
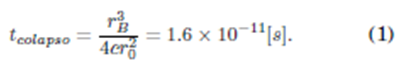
Otra manera de estimar este "tiempo de colapso" es, por supuesto, la de resolver completamente las ecuaciones de movimiento para tal sistema. En lo que sigue, se describirá la respectiva solución numérica, orientada a ese propósito. Simultáneamente, los resultados obtenidos sirven para validar la aproximación del esquema simulador.
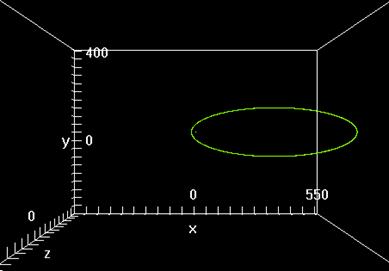
Figure 1: Trayectoria elíptica estable: 20000 puntos calculados con únicamente la fuerza de Coulomb.
ECUACIONES DE MOVIMIENTO
En un sistema aislado con N partículas cargadas, despreciando las interacciones gravitacionales, actúan las fuerzas de Coulomb y las de Abraham-Lorentz; el conjunto se puede escribir:
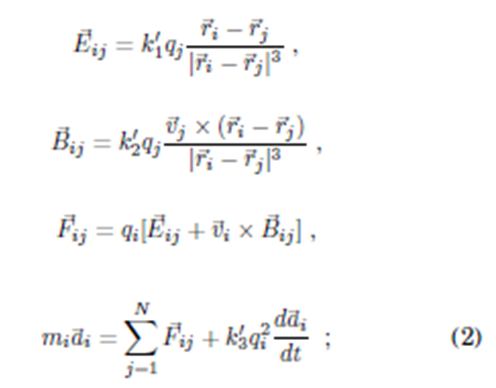
siendo
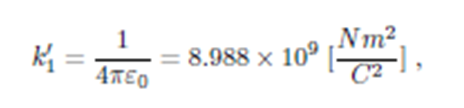
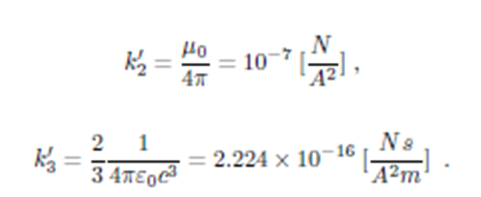
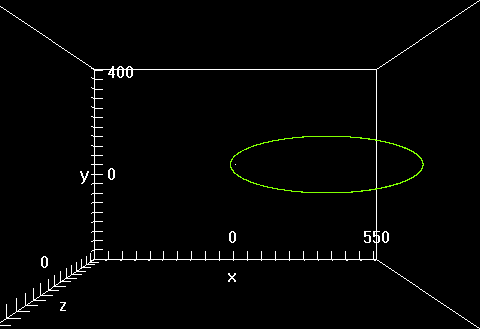
Figure 2: Trayectoria elíptica estable: 20000 puntos calculados con las fuerzas de Coulomb y Lorentz. Casi indistinguible de la que aparece en al fig. 1
El hecho de que, al margen de las variables, las constantes cubren un intervalo de 25 órdenes de magnitud no es relevante para la simulación pues las magnitudes de unas y otras pueden ser dimensionadas internamente; sin embargo, el propósito inmediato aquí es el de verificar la corrección de las soluciones de la ec. (1); entonces, para un tratamiento numérico apropiado es necesaria la renormalización en el siguiente sentido:
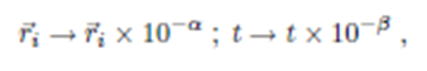
de modo que, agrupando las potencias de 10, una vez que los valores numéricos de todas las magnitudes relevantes (como q=e=1.602×10−16) han sido incluidas en las ecuaciones de movimiento (y absorbidas en las constantes auxiliares k"1,k"2 y k"3), se tiene
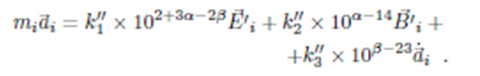
Eligiendo α = 13 y β = 19, se obtiene un esquema numéricamente más manejable:
![]()
con
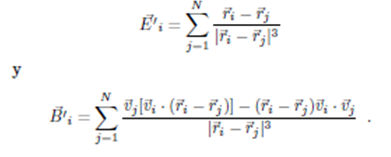
Las constantes devienen

además, puesto que N=2,
m1 = mp = 16726.217 ; m2 = me = 9.109 .
Finalmente, las unidades a emplear durante el cálculo son [→r]=[mÅ] (mili angstroms) y [t]=[das] (deci ato segundos).
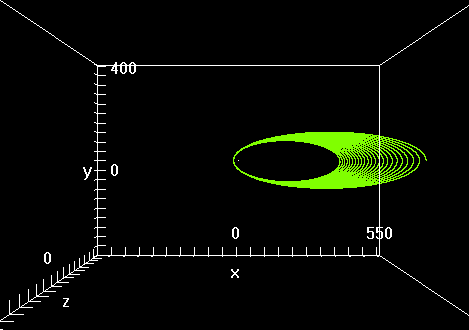
Figure 3: 60000 puntos de la trayectoria espiral elíptica descrita por el electrón sometido a la fuerza de Coulomb-Abraham-Lorentz.
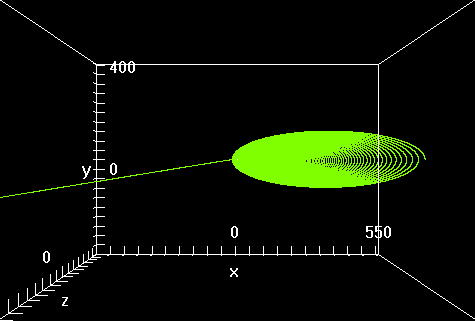
Figure 4: Trayectoria espiral elíptica del electrón hasta el punto de colapso. 340000 puntos en total.
EVOLUCIÓN TEMPORAL DEL ÁTOMO CLÁSICO
La forma de (3) permite "conectar" o "desconectar" cada una de las fuerzas usando el valor inicial de las constantes k o cambiándolo a cero, según el caso. Así, con k2=k3=0 y los valores iniciales obtenidos fijando el radio inicial del electrón igual al radio de Bohr x20=rB=529.2 [mÅ] y variando gradualmente las velocidades iniciales, se logra -sólo para la interacción coulombiana- órbitas estables (figuras 1 y 5).
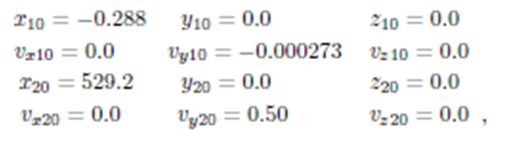
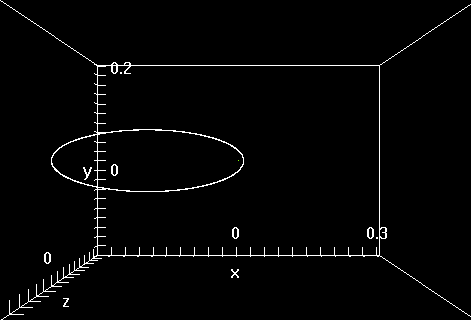
Figure 5: Trayectoria elíptica estable de la carga positiva (el protón). Corresponde a los mismos resultados de los que aparecen en la fig. 1 ampliados aproximadamente 1000 veces (ver las escalas de los ejes x, y).
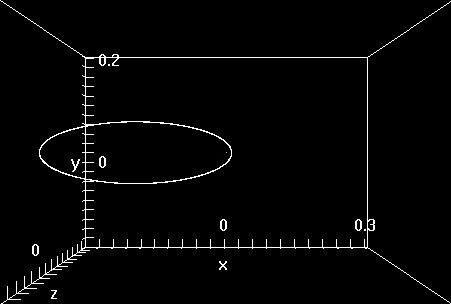
Figure 6: Trayectoria elíptica estable del protón afectado por las fuerzas de Coulomb y Lorentz (20000 puntos).
Las órbitas del electrón y del protón resultantes de la acción adicional de la fuerza de Lorentz (figuras 5 y 6) son casi indistinguibles de las anteriores (figs. 1 y 2). Las velocidades involucradas no son, inicialmente al menos, suficientemente grandes para que el efecto magnético (una pequeña fuerza atractiva) sea numéricamente significativo.
Ahora, el cómputo de las trayectorias cuando la atenuación radiativa se añade a las anteriores interacciones, se muestra en las figuras 3 y 7, correspondiendo al comportamiento esperado: las dos partículas "caen" espiralmente una hacia la otra.
La evaluación iterativa continuada para la fuerza de Coulomb-Abraham-Lorentz implica el "colapso" del sistema. Cuando la distancia alcanza algún valor pequeño ( ≈ 1.4 [mÅ]), el algoritmo diverge. Las soluciones espurias se ven en las figuras 4 y 8 en forma de trazos rectos finales (en direcciones opuestas).
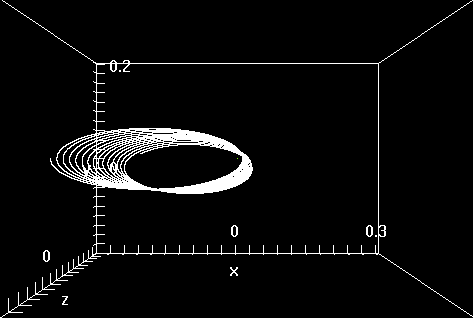
Figure 7: Parte de la trayectoria del protón cuando el frenado por radiación es tomado en cuenta.
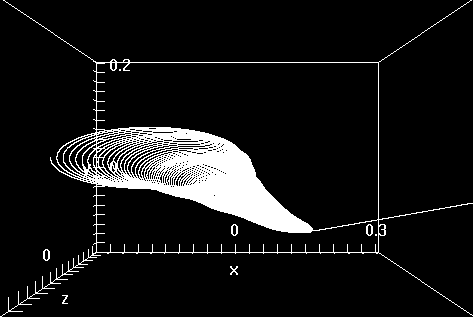
Figure 8: Trayectoria espiral del protón (plano z=0) hasta el punto de colapso. 340000 puntos.
TIEMPO DE COLAPSO
La rutina de cómputo, en cada iteración, determina primero las distancias entre partículas luego, sucesivamente, las componentes cartesianas de las fuerzas de Coulomb y Lorentz usando las expresiones que acompañan a la ec. (3). Para la fuerza de frenado, · →ai requiere el registro de las aceleraciones previas, de modo que · →ai ≈ (· →ai actual−· →ai previo)/∆t. Entonces, hasta el primer orden (Euler), →vi=→ai∆t y, posteriormente, →ri=→vi∆t. El paso ∆t=0.05 [das] mostró ser suficiente para un comportamiento razonablemente rápido y regular.
Como la evolución de las trayectorias concluye cuando, a distancias pequeñas, la ecuación de movimiento produce soluciones espurias, los valores no regulares deben ser ignorados para, mediante un procedimiento de extrapolación, encontrar el tiempo total para el cual |→r1−→r2|=0. Ahora, la distancia interparticular oscila entre máximos y mínimos relativos sucesivos; el seguimiento a éstos es, por supuesto, más útil que el registro completo. La figura 3. muestra esas dos envolventes, desde el punto inicial rB hasta el comienzo de la inestabilidad.
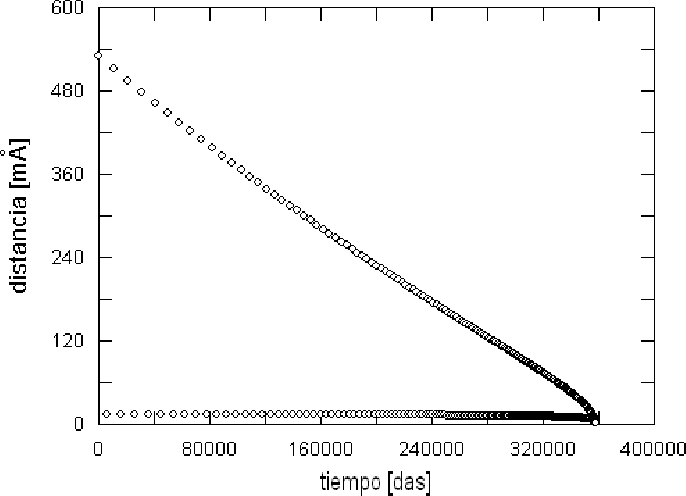
Figure 9: Envolvente del registro de las distancias entre las partículas en función del tiempo (sin tomar en cuenta el paso temporal ∆t).
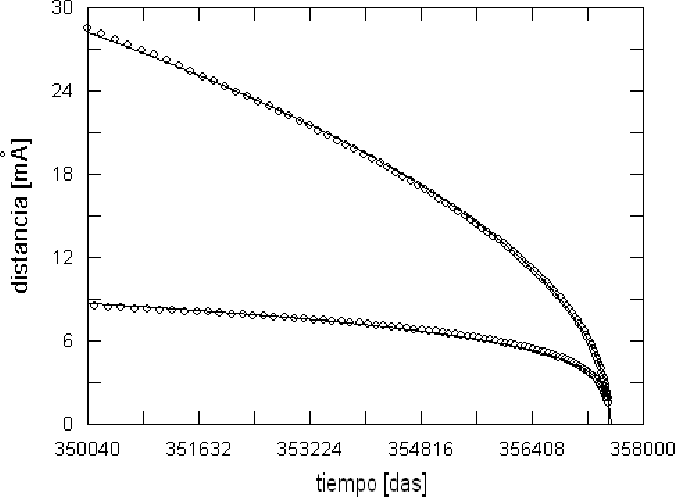
Figure 10: Ajuste de la curva d=a(b−t)1/c a los últimos 92 puntos regulares de la gráfica en la fig. 9. Se advierte la proximidad de los ceros de la ecuación, no obstante la gran diferencia en la inclinación de los valores previos de máximos y m'inimos relativos.
Por otra parte, la figura 10 refleja el tratamiento seguido para encontrar el tiempo de colapso el cual, básicamente, consiste en el ajuste (cuadrados mínimos) de la función
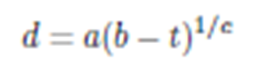
a los últimos 92 puntos del registro de máximos y mínimos relativos; esto es,

y, claro, los valores interesantes son los que corresponden al parámetro b y no todos los dígitos resultan realmente significativos. Basta escribir t=3.575×105[das]; el tiempo de colapso es esta cantidad multiplicada por el paso temporal ∆t, esto es:
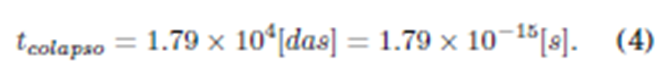
El valor en (4) es cerca de diez mil veces menor que el de (3). Probablemente la diferencia tiene que ver con la forma de la trayectoria -muy elíptica para (3)- y la presencia de la fuerza de Lorentz, cuya magnitud crece al aumentar paulatinamente las velocidades de las partículas.
Conviene notar también que, no obstante la curiosa forma de las trayectorias, especialmente la del protón, todo el proceso tiene lugar en el plano z=0, como debe ser en virtud de la conservación del momento angular.
CONCLUSIONES
La deducción de la ecuación de movimiento de Abraham-Lorentz (2) y la discusión de sus propiedades aparecen detalladas en varios lugares [31975Jackson], [41966Landau & Lifshitz], [21995Hartemann & Luhmann]. La utilidad y el interés del átomo clásico, ya sea para encontrar soluciones estables bajo radiación electromagnética o como límite semiclásico del átomo de Bohr, se refleja en trabajos como [11993Braun] y [61991Uzer et al.Uzer, Farrelly, Milligan, Raines, & Skelton].
La solución numérica emprendida aquí, permite comprobar directamente que la atenuación radiativa -proporcional a la derivada de la aceleración- conduce a resultados aceptables cuando su contribución a la ecuación de movimiento es pequeña -casi como una perturbación-. En el caso presente, esta contribución es intrínsecamente menor en ocho órdenes de magnitud respecto de la fuerza dominante (Coulomb); el descenso espiral de la órbita, entonces, se confirma plenamente.
Por otra parte, el ensayo con los valores iniciales lleva a la inferencia de que las órbitas elípticas son mucho más probables que la circular. Por tanto, el tiempo de colapso estimado a partir de la fórmula de Larmor debe ser una especie de cota superior para los tiempos de colapso.
Finalmente, para los fines que motivaron este trabajo, existe confiabilidad en la simulación de un sistema de N cuerpos cargados a condición de que:
(i) la presencia del término de frenado por radiación se mantenga permanentemente pequeña respecto de las otras fuerzas y
(ii) se prevea en cada iteración -y para todos los componentes del sistema- una restricción a la aproximación excesiva; ello se logra, sin duda, estipulando expresamente, en el algoritmo, que los N cuerpos deben poseer una extensión finita determinada.
Las rutinas computacionales fueron elaboradas específicamente para un entorno amigable que permita ciertos rangos de variación en los parámetros. Se espera que la versión final esté disponible en la interned [52011Peñafiel].
References
1.- Braun, P. A. 1993, Rev. Mod. Phys. 65-1, 115 [ Links ]
2.- Hartemann, F. V. & Luhmann, N. C. 1995, Phys. Rev. Lett. 74-7, 1107 [ Links ]
3.- Jackson, J. D. 1975, Classical Electrodynamics (Second Edition, John Wiley and Sons, Inc.) [ Links ]
4.- Landau, L. D. & Lifshitz, E. M. 1966, Teoría Clásica de los Campos (Reverté S.A.) [ Links ]
5.- Peñafiel, V. M. 2011, http://www.fiumsa.edu.bo [ Links ]
[61991Uzer et al.Uzer, Farrelly, Milligan, Raines, & Skelton]
6.- Uzer, T., Farrelly, D., Milligan, J. A., Raines, P. E., & Skelton, J. P. 1991, Science 253, 42 [ Links ]
Recibido: 22 de julio de 2011; aceptado: 25 de agosto de 2011
File translated from TEX by TTH, version 3.89.
On 25 Feb 2012, 21:08.º














