Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Boliviana de Física
versión On-line ISSN 1562-3823
Revista Boliviana de Física v.19 n.19 La Paz 2011
CARACTERIZACIÓN DE SISTEMAS DINÁMICOS MEDIANTE PERIODICIDADES
Characterization of dynamical systems through periodicities
G. M. Ramírez Ávilaf ,J. A. C. Gallasf
f Instituto de Investigaciones Físicas, Carrera de Física
Universidad Mayor de San Andrés
c. 27 Cota-Cota, Campus Universitario, Casilla de Correos 8639
La Paz - Bolivia
f AG Nichtlineare Dynamik
Institut für Physik
Humboldt Universität zu Berlin
Robert-Koch-Platz 4. Berlín, Alemania
f Instituto de Física
Universidade Federal do Rio Grande do Sul
Departamento de Física
Universidade Federal de Paraiba
58051-970 João Pessoa, Brasil
Resumen
Se caracterizan diferentes sistemas dinámicos descritos por mapas mediante el cálculo de periodicidades. Este método es alternativo a los diagramas de bifurcación utilizando los exponentes de Lyapunov ya que no sólo permite visualizar las estructuras existentes en el espacio de parámetros, tales como los "camarones", sino también proporciona el detalle de los regímenes oscilatorios lo cual puede tener importancia desde el punto de vista práctico.
Descriptores: sistemas dinámicos no-lineales - bifurcación - caos - fractales
Código(s) PACS: 05.45.-a, 05.45.Pq, 05.45.Df
Abstract
We characterize, by means of periodicities, some dynamical systems represented by maps. This is an alternative method to the common bifurcation diagrams computed by using the Lyapunov exponents and allows us to visualize the typical structures onto the parameter space such as the "shrimps" but in addition with the detail of the oscillatory regimes which could be important from a practical viewpoint.
Subject headings: dynamical systems (nonlinear) - bifurcation (nonlinear dynamics) - chaos (numerical simulations) - fractals (nonlinear dynamics)
1 INTRODUCCIÓN
Un aspecto muy importante en el estudio de sistemas dinámicos es el concerniente a los que tienen carácter no lineal lo cual permite estudiar no solamente cuestiones relacionadas a la estabilidad sino también posibles comportamientos caóticos. Los sistemas dinámicos pueden ser representados ya sea por mapas (ecuaciones en diferencia) o mediante flujos continuos (ecuaciones diferenciales). Cuando los sistemas son no lineales, su estudio se encara a menudo de manera numérica puesto que en general es difícil encontrar soluciones analíticas. Aspectos tales como bifurcaciones, periodicidades y caos son parte básica de la denominada Dinámica No Lineal y existen varias formas de abordarlos (ver libros introductorios tales como [41994Argyris et al.Argyris, Faust, & Haase,351995Nicolis,442003Sprott,451994Strogatz,462006Tel & Gruiz]. En el presente trabajo se caracterizan diferentes sistemas dinámicos representados por mapas mediante el cálculo de las periodicidades en los mismos, aspecto que fue desarrollado inicialmente en [161993aGallas,171993bGallas] y más recientemente en [132011aFreire & Gallas,142011bFreire & Gallas,342011Nascimento et al.Nascimento, Gallas, & Varela]. Por otra parte, se compara esta caracterización con otros métodos tales como los diagramas de bifurcación y el cálculo de exponentes de Lyapunov.
El artículo está organizado de la siguiente manera: En la Sección 2 se introduce el mapa logístico y se describen las periodicidades en el mismo. En la Sección 3 se analiza el mapa de Hénon y principalmente la estructura de su espacio de parámetros por medio de periodicidades. En la Sección 4 se analizan algunas regiones del espacio de parámetros del mapa Tinkerbel, donde se encuentran estructuras de periodicidad diferentes a los típicos "camarones". En la Sección 5 se estudia el comportamiento en el espacio de parámetros de un modelo de neurona, en el que parece ser importante el rol que juegan las periodicidades. Finalmente, en la Sección 6 se dan las conclusiones y perspectivas de la investigación realizada.
2 EL MAPA LOGÍSTICO
La denominada ecuación logística surge hace mucho tiempo como modelo alternativo de crecimiento de población diferente al Maltusiano que tiene un carácter exponencial. Su primera formulación se debe al matemático bruselense J. F. Verhulst ([92004Delmas,471838Verhulst]). Este modelo, descrito por una ecuación diferencial, es utilizado ampliamente en demografía y ecología ([152005Gabriel et al.Gabriel, Saucy, & Bersier,321988Meade]). La importancia del trabajo de Verhulst se refleja en los homenajes que se le rindieron conmemorando los 200 años de su nacimiento, especialmente en su ciudad natal donde tuvo lugar la conferencia Verhulst 200 on Chaos de cuyas memorias se editó un libro con una revisión detallada de la ecuación logística y sus aplicaciones ([52005Ausloos & Dirickx]). Sin embargo, este modelo puede ser reducido a un mapa y en esta forma, ser analizado de una manera más simple pero a la vez más profunda. El mapa logístico puede ser expresado en la forma:
![]()
siendo x la variable dinámica y μ el parámetro de control. El análisis del mapa logístico constituye una de los elementos básicos de la dinámica no lineal pues permite estudiar comportamientos que van desde la estacionariedad, pasando por comportamientos periódicos cada vez más complicados hasta llegar al caos (ausencia de periodicidad), solamente variando el parámetro de control.
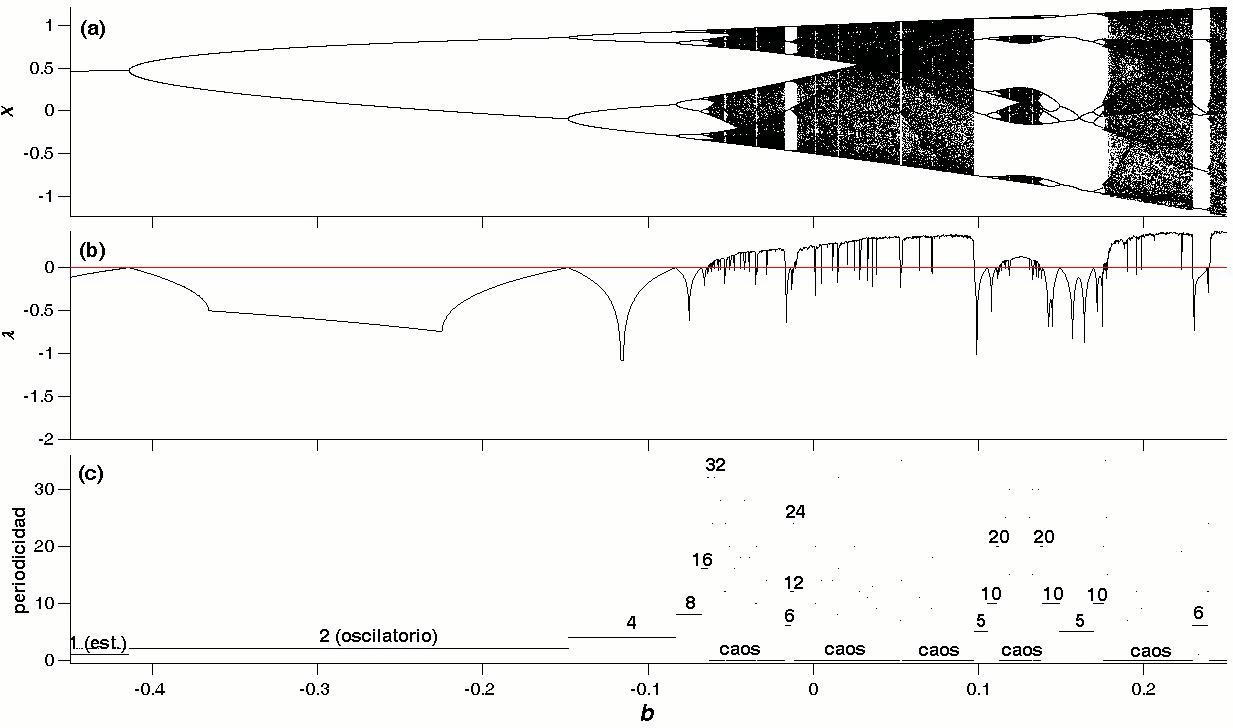
Justamente, el término caos es introducido en 1975 en razón a un estudio del mapa logístico ([261975Li & Yorke]). Numerosos estudios fueron realizados utilizando este simple modelo que sin embargo presenta una dinámica complicada ([311976May]). Particularmente, el aspecto caótico que presenta este sistema para ciertos valores de μ ha sido abordado bajo diferentes perspectivas; desde cálculos sencillos para mostrar el surgimiento de ciclos de período 3 como consecuencia de una bifurcación tangente y que emerge luego de un comportamiento caótico ([61996Bechhoefer,201996Gordon,431995Saha & Strogatz]); hasta el desarrollo de nuevos conceptos tales como el de intermitencia ([221982Hirsch et al.Hirsch, Huberman, & Scalapino]). Por otra parte, partiendo del análisis de las cascadas de desdoblamiento de período en el mapa logístico, se pudieron generalizar y universalizar algunos resultados ([111978Feigebbaum,121979Feigebbaum]). En la Fig. 1 se muestran tres formas de caracterización del mapa logístico: (a) diagrama de bifurcación, (b) exponentes de Lyapunov y (c) periodicidades. Todas estas representaciones nos muestran claramente la diferencia entre comportamiento periódico y caótico; así en la Fig. 1(a) se identifican las cascadas de desdoblamiento de período y las regiones oscuras del diagrama representan situaciones de caos. En la Fig. 1(b), las regiones periódicas se diferencian de las caóticas en que para las periódicas, el exponente de Lyapunov es negativo (λ ≤ 0), en tanto que para las caóticas, es positivo (λ > 0). La distribución de periodicidades se muestra como una especie de escalones en la Fig. 1(c), correspondiendo al escalón cero el comportamiento caótico del sistema.
Lo interesante de trabajar con periodicidades radica en el hecho de identificar más finamente el comportamiento oscilatorio del sistema, lo cual no queda muy claro en las otras representaciones. Sin embargo, una desventaja es que para tener una buena determinación de las periodicidades, es necesario un proceso de iteración largo; lo anterior se aplica también al cálculo de exponentes de Lyapunov pues se debe alcanzar la estabilidad de estos.
Para finalizar esta sección, se debe resaltar el hecho de que el mapa logístico es quizás el ejemplo tomado más a menudo para encarar el estudio de nuevos conceptos. Ver por ejemplo: [272005Lind et al.Lind, Gallas, & Herrmann,302005Masoller & Marti].
3 EL MAPA DE HENÓN
En 1976, Hénon propone un modelo reduccionista ([211976Hénon]) capaz de reproducir de modo computacionalmente más simple los resultados provenientes del paradigmático modelo de Lorenz ([281963Lorenz]). En su forma más sencilla puede expresarse como:
![]()
Esta transformación tiene como una de sus características más importantes la de preservar el área en el espacio de fases cuando |b|=1 puesto que J=1; siendo J, el determinante jacobiano, lo que significa que bajo esta condición, el sistema que describe es conservativo. Un gran número de estudios ha sido realizado acerca del mapa de Hénon, entre los que podemos destacar el análisis de desdoblamientos de período ([71981Bountis]),, el análisis de puntos fijos que dan lugar a ciclos límites con diferentes períodos ([231985Hitzl & Zele]); la exploración exhaustiva en el espacio de parámetros donde se encuentran las estructuras de "camarón" ([171993bGallas,292008Lorenz]); el análisis con diagramas isoperiódicos ([81993Cabral et al.Cabral, Lago, & Gallas,181994Gallas]) y de las cuencas de atracción ([392005Rech et al.Rech, Beims, & Gallas]), entre otros.
La ruta al caos en el mapa de Hénon puede ocurrir a través de una cascada de desdoblamiento de período como se muestra en la Fig. 2 en la que se fija el valor del parámetro a y se varía b. Se hace la misma caracterización que para el mapa logístico y se observan algunos aspectos importantes tales como bifurcaciones con colisiones de borde similares a las expuestas en [361994Nusse et al.Nusse, Ott, & Yorke,371992Nusse & Yorke]. Volveremos sobre este aspecto en el estudio del mapa Tinkerbell.
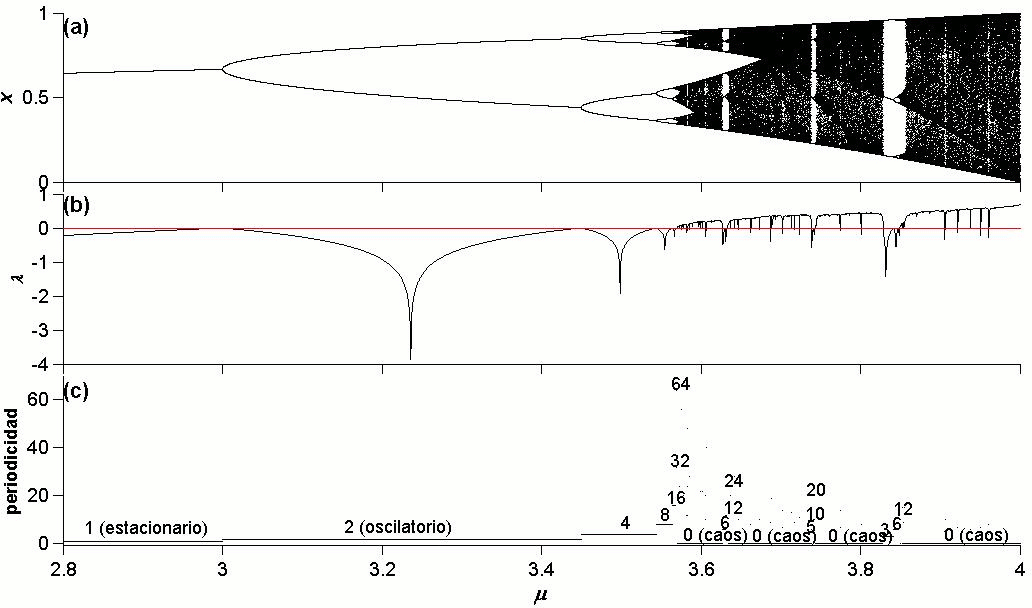
Figure 1: (Color online) Caracterización dinámica del mapa logístico en función del parámetro de control μ, mediante (a) un diagrama de bifurcación, (b) los exponentes de Lyapunov y (c) las periodicidades.
Figure 2: (Color online) Caracterización dinámica del mapa de Hénon en función del parámetro de control b, mediante (a) un diagrama de bifurcación, (b) los exponentes de Lyapunov y (c) las periodicidades, cuando a=1.5.
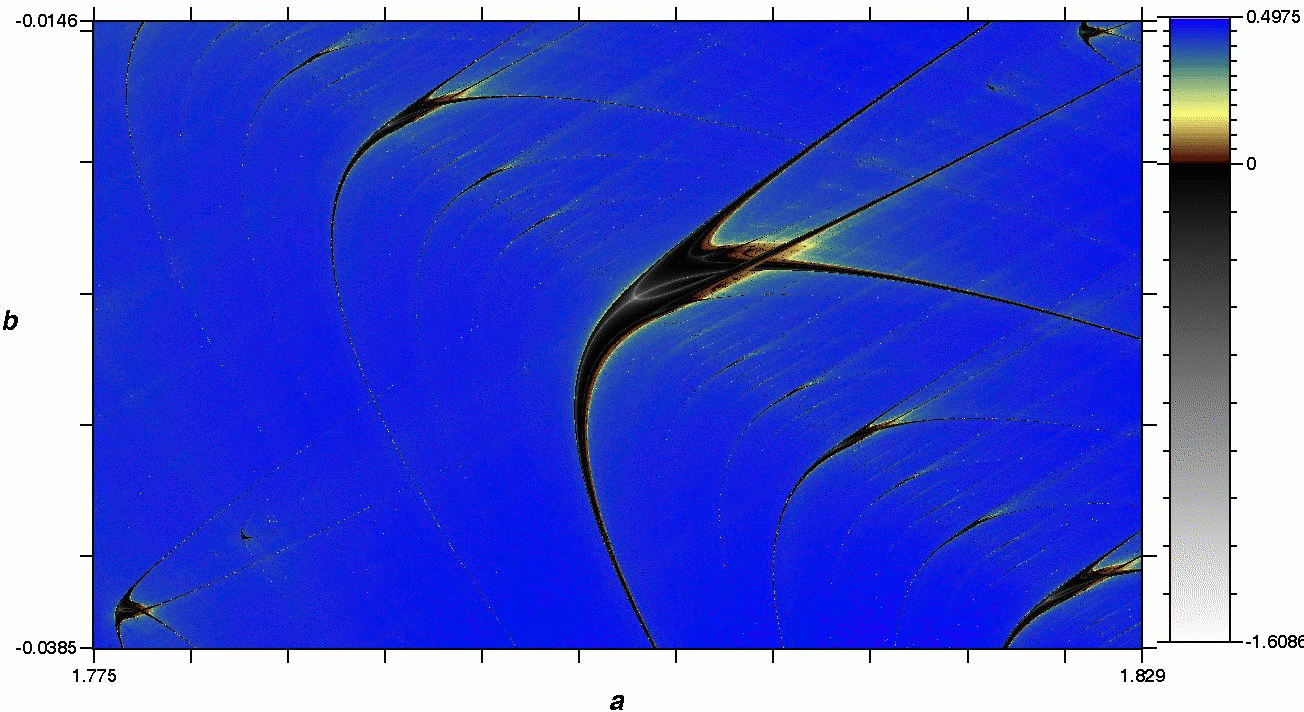
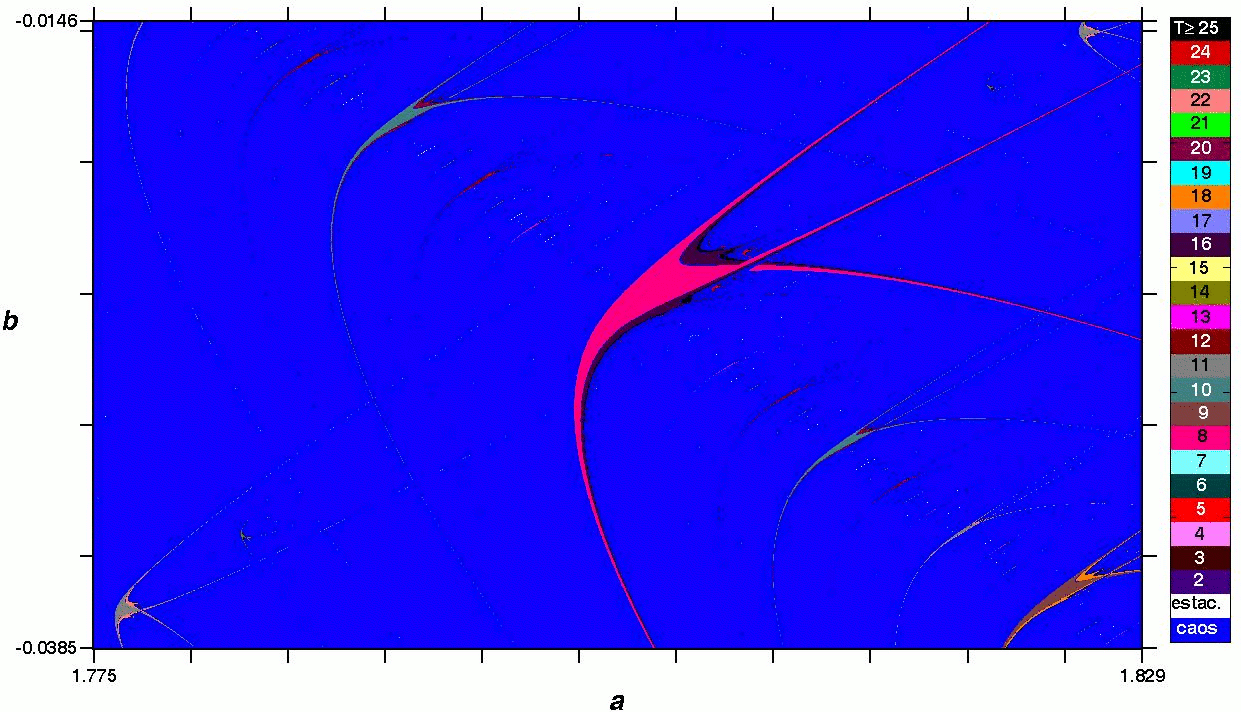
En la Fig. 3, mostramos un diagrama de fases para el mapa de Hénon, considerando los mayores exponentes de Lyapunov (a) y las periodicidades (b). Utilizando la misma región que se reporta en [171993bGallas]. Como se puede notar, las estructuras que denotan comportamiento periódico tienen la forma de "camarones". Del diagrama obtenido a partir de los mayores exponentes de Lyapunov, si bien se pueden identificar algunas regiones de superestabilidad al interior de los camarones, aparte de eso, no se pueden identificar las periodicidades que corresponden a cada una de estas estructuras lo que se consigue fácilmente si se utiliza el diagrama de periodicidades. Es interesante observar que los camarones no son completamente isoperiódicos y que en los bordes de los mismos existen desdoblamientos de período que como es natural, conducen a la región caótica.
4 MAPA TINKERBELL
(a)
(b)
Figure 3: (Color online) Espacio de parámetros del mapa de Hénon obtenido a partir de (a) los mayores exponentes de Lyapunov y (b) las periodicidades; en este caso, cada color de la barra a la derecha corresponde a una determinada periodicidad; las situaciones de caos y estacionariedad están indicadas por los colores de los cuadros inferiores (azul y blanco respectivamente) y la situación en que la periodicidad es mayor o igual a 25 por el color negro, correspondiente al cuadro superior de la barra.
El mapa Tinkerbell, aparece en general como un ejemplo académico de sistema dinámico ([31996Alligood et al.Alligood, Sauer, & Yorke,442003Sprott]). Sin embargo, dadas sus características, ofrece una riqueza dinámica que puede ser explotada. La forma explícita de este mapa es:
![]()
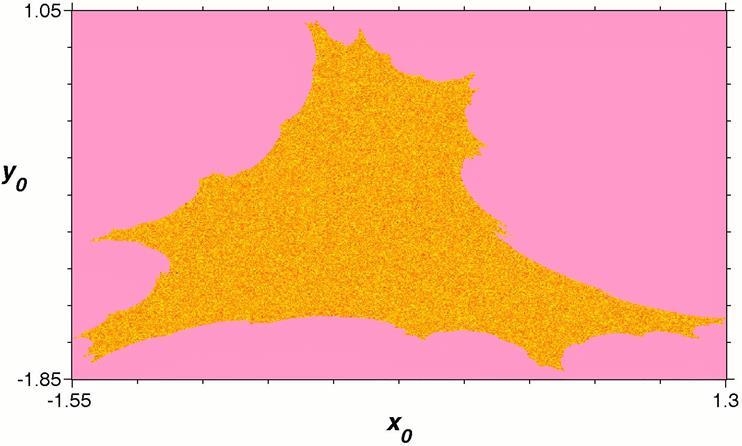
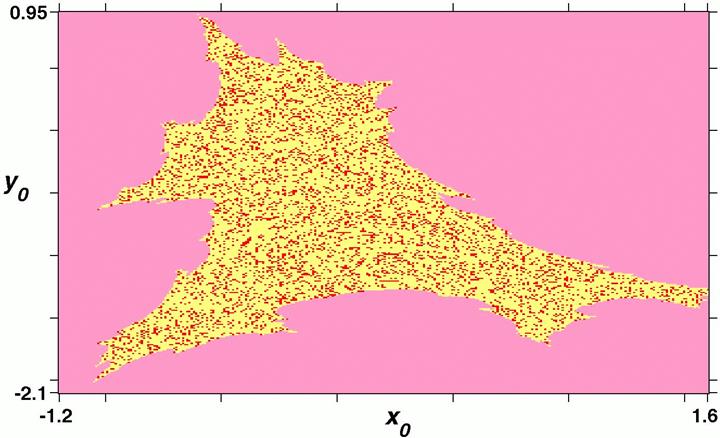
Una de sus características es la de presentar una estructura fractal en las fronteras de la cuenca de atracción, tal como se observa en la Fig. 4. La forma de la cuenca de atracción es geométricamente la misma para otros valores de los parámetros a pesar de que el comportamiento pueda resultar totalmente diferente. Así, se puede tener una cuenca completamente caótica como la de la Fig. 4(a) o una cuenca completamente periódica con otros valores de parámetros, tal como se muestra en la Fig. 4(b).
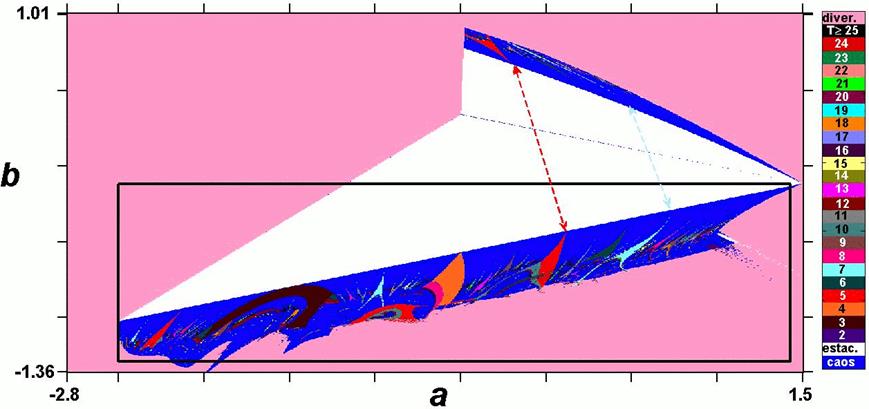
Por otra parte, dado que existen 4 parámetros de control en el modelo, se pueden obtener diferentes secciones del espacio de parámetros, cada una de las cuales tiene aspectos interesantes a estudiar. Por simplicidad, nos abocaremos a la sección del espacio de parámetros (a, b) que se muestra en la Fig. 5. Como se pudo observar en la Fig. 4, existen muchas regiones en las cuales se tiene divergencia; sin embargo, se pueden localizar regiones en las cuales existen estructuras periódicas rodeadas de caos. En la Fig. 5(a) se ven dos de estas regiones separadas por una región donde el comportamiento del sistema es estacionario.
(a)
(b)
Figure 4: (Color online) Cuencas de atracción (a) caótica para el modelo Tinkerbell cuando los valores de los parámetros son: a=0.5, b=−0.6, c=2.2 y d=0.5. (b) periódica con a=−0.51, b=−0.9, c=2.2 y d=0.5. Las regiones rojas corresponden a periodicidades de orden 5 en tanto que las amarillas son de orden 15. En ambos casos, la zona rosa indica que para esos valores de parámetros, no se tiene convergencia.
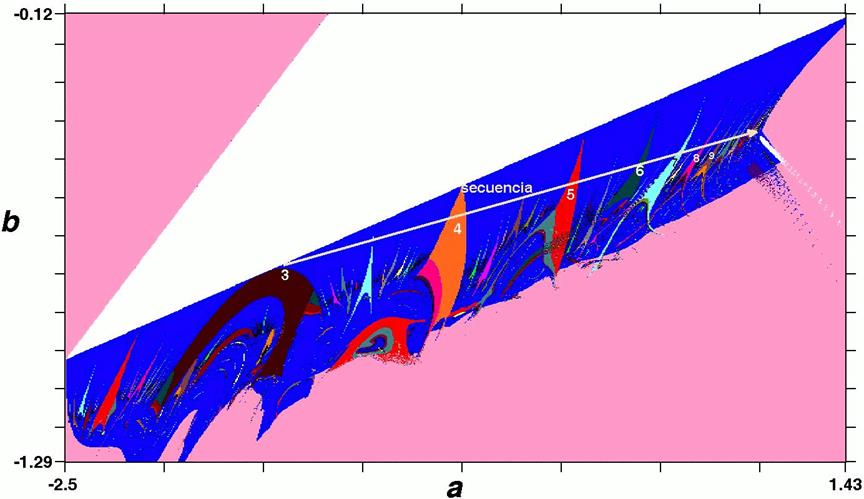
También, se ve que parece haber una suerte de conexión entre estructuras de igual periodicidad, lo que se resalta mediante flechas para el caso de periodicidades 5 y 7. Es interesante observar en la Fig. 5(b), una de estas regiones, en la cual se nota la presencia de secuencias de camarones y otras estructuras periódicas que indican rutas degeneradas al caos similares a las encontradas en [161993aGallas]. En particular, la secuencia que va de periodicidad 1 a ∞ y que se muestra con la flecha blanca. Por supuesto, existen otras secuencias considerando estas mismas estructuras multiperiódicas. Así, se tendrán por ejemplo, secuencias:

La forma en la que se distribuyen las regiones periódicas nos lleva a pensar que la ruta al caos no necesariamente ocurre a través de una cascada de desdoblamiento de período y que más bien tienen lugar otro tipo de bifurcaciones como la de colisiones de frontera que se mencionó al analizar el mapa de Hénon. Se ve también la existencia de estructuras periódicas menores y cuyas periodicidades también parecen seguir una cierta secuencia. Por último, se debe señalar también que las estructuras periódicas encontradas en el mapa Tinkerbell, tienen una morfología diferente a la de los "camarones" que se encuentra en la mayor parte de los sistemas dinámicos, tanto discretos como continuos.
5 UN MODELO DE NEURONA
Como es sabido, el cerebro -en particular de los humanos- es uno de los sistemas complejos más difíciles de analizar y aunque en los últimos años se ha avanzando considerablemente en Neurociencia, hay todavía aspectos que permanecen oscuros en relación a la funcionalidad del mismo. El cerebro tiene como piezas fundamentales a las neuronas que pueden llegar en número a 1011. Estas neuronas están conectadas entre sí formando redes altamente complejas pues el número de vínculos que puede tener cada neurona puede llegar a 104.
Existen diferentes tipos de neuronas y desde hace muchos años se ha tratado de modelizar las mismas tanto individualmente como cuando se conectan a otras. Una neurona es considerada como un sistema que no está en equilibrio y que además posee varios mecanismos de retroalimentación y de retardo, los cuales permiten el carácter oscilatorio de la misma ([11996Abarbanel et al.Abarbanel, Rabinovich, Selverston, Bazhenov, Huerta, Sushchik, & Rubchinsky]). Una de las características del comportamiento de las neuronas es la de poseer excitabilidad eléctrica. Por otra parte, se destacan el potencial de reposo y el potencial de acción como típicos en el funcionamiento neuronal. Dado que existen muchos tipos de neuronas y cada una de ellas con diferentes características, se han propuesto diferentes modelos para la descripción de las mismas. El primer modelo propuesto fue el de Hodgkin-Huxley en 1952 ([241952Hodgkin & Huxley]) que fue la parte culminante de una serie de trabajos experimentales con neuronas de calamar gigante.
(a)
(b)
Figure 5: (Color online) Espacio de parámetros (a, b) para el mapa Tinkerbell utilizando periodicidades para su caracterización. (a) Dos regiones que presentan estructuras periódicas y caos, separadas por una región de estacionariedad. (b) Magnificación de la región encuadrada en (a), donde se observan secuencias bien definidas en las estructuras mayores y otras para las menores. La flecha blanca indica una secuencia en la que participan las regiones periódicas de mayor tamaño..Se utiliza para denotar las periodicidades un código de colores similar al de la Fig. 3, donde enfatizamos que la región azul corresponde a caos, la blanca a estacionariedad y la rosa a divergencia.
Posteriormente, se postularon otros modelos que trataron de expresar de forma más simple las ecuaciones que gobiernan el comportamiento de las neuronas. Todos estos modelos consisten en sistemas de ecuaciones diferenciales no lineales por lo que su solución analítica resulta casi imposible. Es así, que en general se aborda el problema de manera numérica. Con el afán de simplificar estos modelos, Rulkov plantea un modelo consistente en un mapa con dos variables que permite rescatar los comportamientos más importantes en las neuronas, tales como el hecho de tener oscilaciones sostenidas, situaciones de estacionariedad y las denominadas ráfagas o "bursts" consistentes en episodios oscilatorios de tipo "spikes" (picos) seguidos por fases de estacionariedad o "silencio" ([412001Rulkov,422002Rulkov]). El modelo se expresa por:
![]()
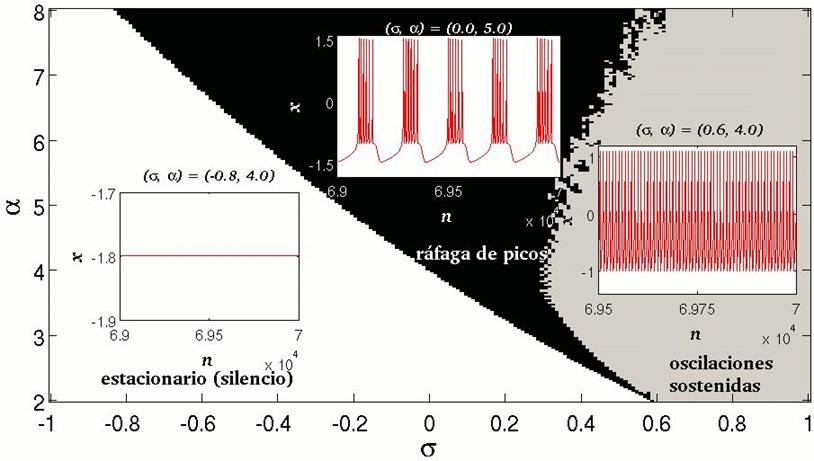
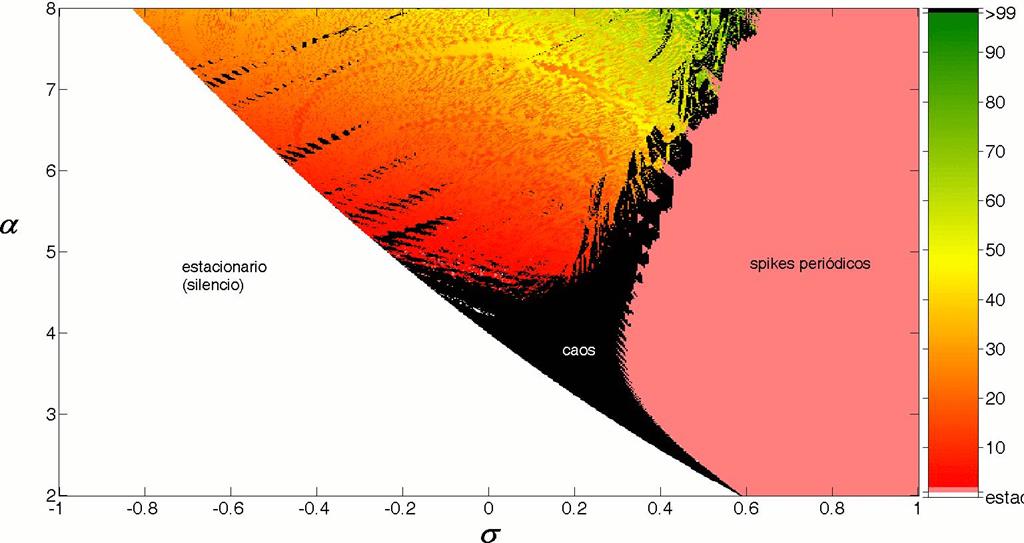
donde x y y son las variables dinámicas rápida y lenta respectivamente cuando el parámetro μ toma valores pequeños como por ejemplo μ = 0.001. Siguiendo los valores típicos considerados en [422002Rulkov], se pueden determinar 3 regiones en el espacio de parámetros (σ,α), tal como se muestra en la Fig. 6; estos parámetros son los que determinan el comportamiento de la neurona y están en relación con las influencias externas aplicadas. En los recuadros, se observan los comportamientos típicos de la variable x.
Figure 6: (Color online) Regiones en el espacio de parámetros (σ,α), donde se distinguen las regiones de estacionariedad o silencio, la de oscilaciones sostenidas (spikes) y la de ráfagas de picos (burst of spikes), donde los recuadros muestran ejemplos de la evolución temporal de la variable x en cada una de estas regiones.
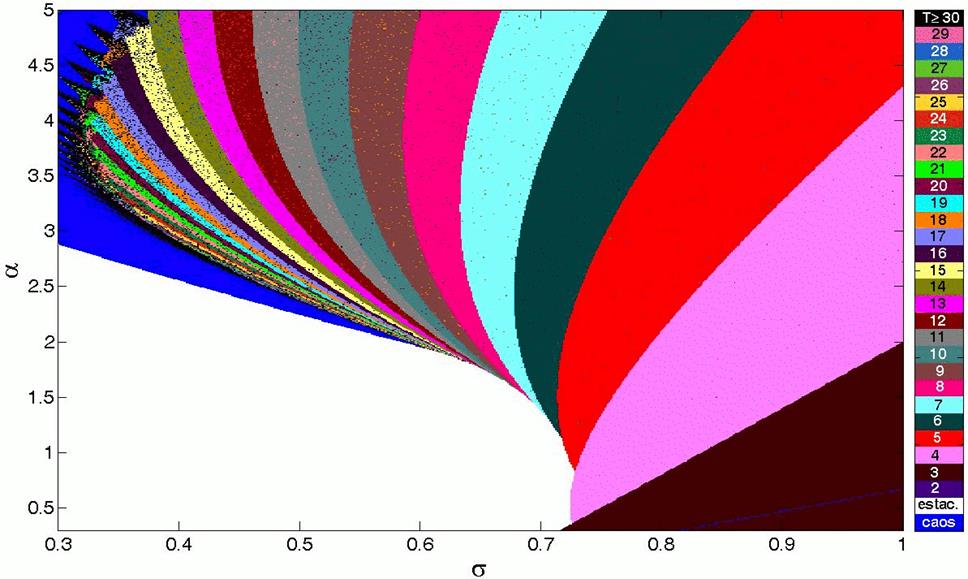
Figure 7: (Color online) Periodicidades en el espacio de parámetros del modelo de Rulkov. Se utiliza un código de colores similar al de la Fig. 3 con el objeto de identificar las regiones de estacionariedad y caos.
Como se puede ver, la determinación de la frontera entre la región de "ráfagas de picos" ("burst of spikes") y la región de picos continuos (oscilaciones sostenidas) no queda muy bien delimitada; en particular, la región inferior de la "ráfaga de picos" podría ser considerada con más propiedad como una región de oscilaciones en las que existe un impulso como si se tratase de una función delta de Dirac y que además, como se explicitará posteriormente en la Fig. 9(a), se trata de una región caracterizada por un comportamiento caótico. Para un análisis más fino, se procede en la Fig. 7 a estudiar con mayor detalle esta área del espacio de parámetros.
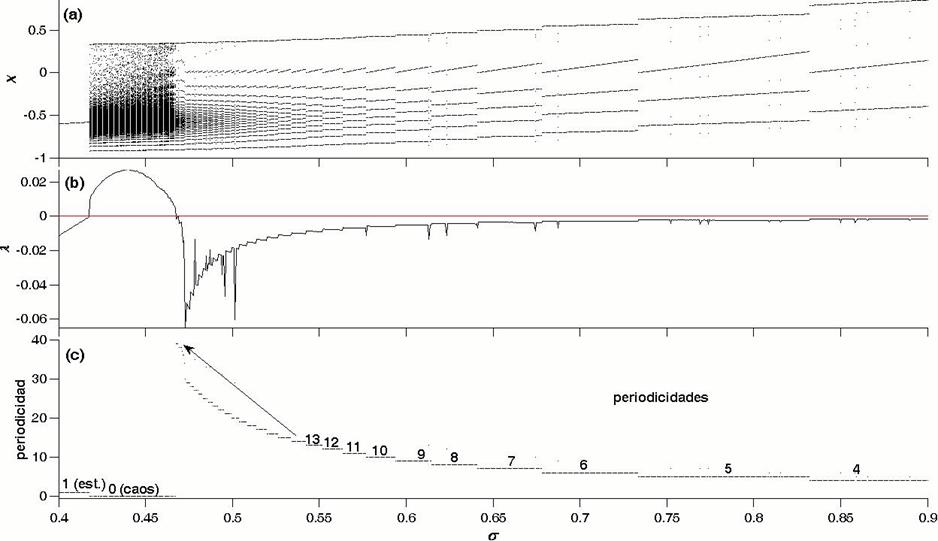
Llamamos también la atención sobre el hecho de que las fronteras reportadas en [422002Rulkov] no coinciden plenamente con las que nosotros determinamos haciendo un exhaustivo barrido de los valores de los parámetros. Como se puede ver en la Fig. 7, las periodicidades en la región de oscilaciones sostenidas están bien definidas y disminuyen en pasos de 1 luego de que el sistema sale de la ventana caótica. Es interesante notar también que las áreas correspondientes a periodicidades menores aumentan a medida que la periodicidad disminuye, lo que es coherente si se piensa que la ruta al caos implica ventanas de periodicidad cada vez más estrechas. Para tener una idea más clara de cómo ocurre la bifurcación, se representa en la Fig. 8, la misma caracterización dinámica utilizada en las Figs. 1 y 2, donde es interesante observar el paso de la estacionariedad al caos sin mediar una cascada de desdoblamiento de período.
Figure 8: (Color online) Caracterización dinámica para el modelo de Rulkov en función del parámetro de control σ, mediante (a) un diagrama de bifurcación, (b) los exponentes de Lyapunov y (c) las periodicidades,.cuando α = 2.5 y μ = 0.001.
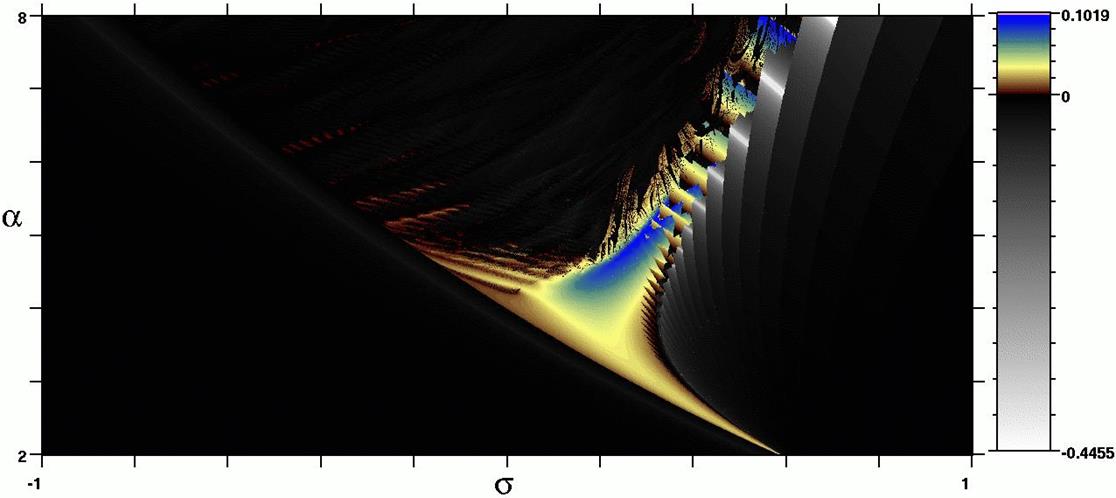
Para finalizar nuestro análisis del modelo de neurona, nos concentramos en la región donde se tienen las ráfagas de picos pues en algunos sectores de la misma se presenta un comportamiento caótico. En la Fig. 9(a) se representa esta región mediante exponentes de Lyapunov y en la Fig. 9(b) a través de un análisis contando el número de picos de las ráfagas, cuando estas son periódicas. Se observa que el número de picos en las ráfagas tiende a aumentar cuando los parámetros σ y α crecen. Debemos mencionar también que variando el valor del parámetro μ para las mismas regiones del espacio de parámetros (σ,α), se observa que la región caótica es mayor cuando el valor de μ disminuye.
Existen otros modelos de neurona basados en mapas cuyas descripciones se exponen en [252011Ibarz et al.Ibarz, Casado, & Sanjuán].
(a)
(b)
Figure 9: (Color online) Espacio de parámetros para el modelo de Rulkov considerando (a) los exponentes de Lyapunov. La barra de colores indica el valor de los mayores exponentes de Lyapunov. (b) El número de picos por ráfaga; en negro se representan las regiones caóticas y en colores las regiones donde existe periodicidad. La región blanca significa que no existen ráfagas de picos.
6 CONCLUSIONES Y PERSPECTIVAS
En primer lugar, se verificó la pertinencia del cálculo de periodicidades como una alternativa útil y sencilla para la caracterización de sistemas dinámicos.
Comparando las caracterizaciones mediante exponentes de Lyapunov y periodicidades, una de las ventajas de trabajar con las últimas es la de poder discriminar cada orden de periodicidad y verificar las posibles secuencias de las mismas que permiten tener una idea más clara de cómo se presenta la ruta hacia el caos. Sin embargo, uno de los problemas de trabajar con periodicidades es el de tener que considerar tiempos bastante largos en las regiones donde se presentan las bifurcaciones pues de lo contrario, se obtienen resultados erróneos que parecerían mostrar caos en todas las fronteras entre periodicidades.
El análisis de modelo de neurona de Rulkov muestra resultados interesantes pues nos permite identificar 3 zonas con características bien definidas. En la región de oscilaciones sostenidas, la ruta al caos ocurre a través de una cascada pero no con desdoblamiento de período sino con un aumento discreto de la periodicidad (en pasos de uno). Por otro lado, la salida del caos es directamente hacia la estacionariedad. Adicionalmente, el análisis en la región donde se presentan ráfagas de picos, nos indica que existen regiones caóticas que podemos identificarlas mediante el cálculo de exponentes de Lyapunov y además, se puede también describir el comportamiento de estas ráfagas mediante la cuantificación del número de picos por ráfaga cuando estas ráfagas son periódicas. Esto es importante puesto que permite escoger el comportamiento de acuerdo al sistema que se estudia. Este tipo de comportamiento, se observa también en algunas especies de luciérnagas macho ([331995Moiseff & Copeland,382011Ramírez et al.Ramírez, Deneubourg, Guisset, Wessel, & Kurths]) y este modelo eventualmente podría ser aplicado para estudiar la emisión de flashes de estos insectos. Otra aplicación de esta clase de modelo se puede dar en sistemas que describen ritmos biológicos en los que ocurren ráfagas de picos como los que se mencionan en [191996Goldbeter] y más específicamente en lo referente a oscilaciones de Ca2+ ([102009Dupont & Combettes]). Es importante el estudio de mapas similares no sólo individualmente sino también formando redes tal como lo hacen las neuronas.
El análisis de periodicidades puede ser relacionado con ciertas series típicas como la de Farey estudiadas en otros sistemas que presentan multiestabilidades como en [21989Albahadily et al.Albahadily, Ringland, & Schell,401990Ringland et al.Ringland, Issa, & Schell] y aún más recientemente en [142011bFreire & Gallas]. Finalmente, el análisis de periodicidades puede ser reemplazado por un análisis de conteo de picos en series de tiempo periódicas provenientes de sistemas continuos tal como se hizo en [142011bFreire & Gallas].
GMRA agradece al Deutscher Akademischer Austausch Dienst (DAAD) por la beca de investigación otorgada. JACG agradece al Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) por el financiamiento para la investigación y también agradece a la Air Force Office of Scientific Research (AFOSR) por el apoyo bajo contrato FA9550-07-1-0102.
References
[11996Abarbanel et al.Abarbanel, Rabinovich, Selverston, Bazhenov, Huerta, Sushchik, & Rubchinsky]
1.- Abarbanel, H. D., Rabinovich, M. I., Selverston, A., Bazhenov, M. V., Huerta, R., Sushchik, M. M., & Rubchinsky, L. L. 1996, Physics-Uspekhi 39, 337 [ Links ]
[21989Albahadily et al.Albahadily, Ringland, & Schell]
2.- Albahadily, F. N., Ringland, J., & Schell, M. 1989, The Journal of Chemical Physics 90, 813 [ Links ]
[31996Alligood et al.Alligood, Sauer, & Yorke]
3.- Alligood, K., Sauer, T. D., & Yorke, J. A. 1996, Chaos: An Introduction to Dynamical Systems (Springer-Verlag, New York) [ Links ]
[41994Argyris et al.Argyris, Faust, & Haase]
4.- Argyris, J., Faust, G., & Haase, M. 1994, An Exploration to Chaos (Elsevier Science B. V., Amsterdam) [ Links ]
4.- Ausloos, M. & Dirickx, M. 2005, The Logistic Map: Map and the Route to Chaos: From the Beginning to Modern Applications (Springer-Verlag, Heidelberg) [ Links ]
5.- Bechhoefer, J. 1996, Mathematics Magazine 69, 115 [ Links ]
6.- Bountis, T. C. 1981, Physica D 3, 577 [ Links ]
[81993Cabral et al.Cabral, Lago, & Gallas]
7.- Cabral, F., Lago, A., & Gallas, J. A. C. 1993, International Journal of Modern Physics C 4, 553 [ Links ]
8.- Delmas, B. 2004, Math. & Sci. hum./ Mathematics and Social Sciences 167, 51 [ Links ]
9.- Dupont, G. & Combettes, L. 2009, Chaos 19, 037112 [ Links ]
10.- Feigebbaum, M. J. 1978, J. Stat. Phys. 19, 25 [ Links ]
11.- -. 1979, J. Stat. Phys. 21, 669 [ Links ]
12.- Freire, J. G. & Gallas, J. A. C. 2011a, Physical Chemistry Chemical Physics 13, 12191 [ Links ]
13.- -. 2011b, Phys. Lett. A 375, 1097 [ Links ]
[152005Gabriel et al.Gabriel, Saucy, & Bersier]
14.- Gabriel, J. P., Saucy, F., & Bersier, L. F. 2005, Ecological Modelling 185, 147 [ Links ]
15.- Gallas, J. A. C. 1993a, Phys. Rev. E 48, R4156 [ Links ]
16.- -. 1993b, Phys. Rev. Lett. 70, 2714 [ Links ]
17.- -. 1994, Physica A 202, 196 [ Links ]
18.- Goldbeter, A. 1996, Biochemical Oscillations and Cellular Rhythms. The Molecular Bases of Periodic and Chaotic Behaviour (Cambridge University Press, Cambridge) [ Links ]
19.- Gordon, W. B. 1996, Mathematics Magazine 69, 118 [ Links ]
20.- Hénon, M. 1976, Communications in Mathematical Physics 50, 69 [ Links ]
[221982Hirsch et al.Hirsch, Huberman, & Scalapino]
21.- Hirsch, J. E., Huberman, B. A., & Scalapino, D. J. 1982, Phys. Rev. A 25, 519 [ Links ]
22.- Hitzl, D. L. & Zele, F. 1985, Physica D 14, 305 [ Links ]
23.- Hodgkin, A. L. & Huxley, A. F. 1952, Journal of Physiology 117, 500 [ Links ]
[252011Ibarz et al.Ibarz, Casado, & Sanjuán]
24.- Ibarz, B., Casado, J. M., & Sanjuán, M. A. F. 2011, Phys. Rep. 501, 1 [ Links ]
25.- Li, T. Y. & Yorke, J. A. 1975, The American Mathematical Monthly 82, 985 [ Links ]
[272005Lind et al.Lind, Gallas, & Herrmann]
26.- Lind, P. G., Gallas, J. A. C., & Herrmann, H. J. 2005, Coherence in Complex Networks of Oscillators, 77, in the Logistic Map: Map and the Route to Chaos: From the Beginning to Modern Applications (Springer Verlag, Heidelberg) [ Links ]
27.- Lorenz, E. N. 1963, Journal of the Atmospheric Sciences 20, 130 [ Links ]
28.- -. 2008, Physica D 237, 1689 [ Links ]
29.- Masoller, C. & Marti, A. C. 2005, Phys. Rev. Lett. 94, 134102 [ Links ]
30.- May, R. M. 1976, Nature 261, 459 [ Links ]
31.- Meade, N. 1988, Journal of the Royal Statistical Society.Series A (Statistics in Society)151, 491 [ Links ]
32.- Moiseff, A. & Copeland, J. 1995, J. Insect Behav. 8, 395 [ Links ]
[342011Nascimento et al.Nascimento, Gallas, & Varela]
33.- Nascimento, M. A., Gallas, J. A. C., & Varela, H. 2011, Physical Chemistry Chemical Physics 13, 441 [ Links ]
34.- Nicolis, G. 1995, Introduction to Nonlinear Science (Cambridge University Press, Cambridge) [ Links ]
[361994Nusse et al.Nusse, Ott, & Yorke]
35.- Nusse, H. E., Ott, E., & Yorke, J. A. 1994, Phys. Rev. E 49, 1073 [ Links ]
36.- Nusse, H. E. & Yorke, J. A. 1992, Physica D 57, 39 [ Links ]
[382011Ramírez et al.Ramírez, Deneubourg, Guisset, Wessel, & Kurths]
37.- Ramírez, G. M., Deneubourg, J. L., Guisset, J. L., Wessel, N., & Kurths, J. 2011, EPL (Europhysics Letters) 94, 60007 [ Links ]
[392005Rech et al.Rech, Beims, & Gallas]
38.- Rech, P. C., Beims, M. W., & Gallas, J. A. C. 2005, Phys. Rev. E 71, 017202 [ Links ]
[401990Ringland et al.Ringland, Issa, & Schell]
39.- Ringland, J., Issa, N., & Schell, M. 1990, Phys. Rev. A 41, 4223 [ Links ]
40.- Rulkov, N. F. 2001, Phys. Rev. Lett. 86, 183 [ Links ]
41.- -. 2002, Phys. Rev. E 65, 041922 [ Links ]
42.- Saha, P. & Strogatz, S. 1995 [ Links ]
43.- Sprott, J. C. 2003, Chaos and Time-Series Analysis (Oxford University Press) [ Links ]
44.- Strogatz, S. H. 1994, Nonlinear Dynamics and Chaos. With Applications to Physics, Biology, Chemistry and Engineering (Perseus Books, New York) [ Links ]
45.- Tel, T. & Gruiz, M. 2006, Chaotic Dynamics. An Introduction Based on Classical Mechanics (Cambridge University Press, Cambridge) [ Links ]
46.- Verhulst, P. F. 1838, Correspondance Mathématique et Physique 10, 113 [ Links ]
Recibido 9 de mayo de 2011; aceptado 10 de junio de 2011
File translated from TEX by TTH, version 3.89.
On 28 Feb 2012, 14:09.