Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Boliviana de Física
versión On-line ISSN 1562-3823
Revista Boliviana de Física v.15 n.15 La Paz 2009
1ra OLIMPIADA ANDINA DE ASTRONOMÍA Y ASTROFÍSICA
BUSTOS R.1, DE LA TORRE M.2, RAMIREZ M.1 , ZUBIETA V.1, BRAÑEZ A.1, MIRANDA P. 1 , MUÑOZ R.1, RALJEVIC M.1 , GARCIA J.1 ,
CENTENO E. 1 , POMA J. 1 , MAYTA R.1 , PEÑAFIEL M.1 , CORDERO M. 2 , TAVERA W. 3 , CARVAJAL R. 4 , CABRERA S. 4 , LANDIVAR M. 4 ,
CERRUTO I. 4 , ORELLANA W. 4 , SANTALLA I. 5 , PEREYRA S. 5 , ANDRADE M. 6 , VALLEJOS V. 7
1 Universidad Mayor de San Andrés (UMSA), Carrera de Física, La Paz
2 Asociación Boliviana para el Avance de la Ciencia (ABAC)
3 Sociedad Boliviana de Física (SOBOFI)
4 Ministerio de Planificacion para el Desarrollo, Viceministerio de Ciencia y Tecnología
5 Estudiantes exolímpicos
6 Universidad Mayor de San Simon (UMSS), Carrera de Física, Cochabamba
7 Astrónomo, UMSA
RESUMEN
La 1ra Olimpiada Andina de Astronomía y Astrofísica (1ra OAAA) nace de la necesidad de dar una urgente respuesta al desafío sobre: ¿Como incentivar a la juventud de nuestros países al estudio de la Astronomía y la Astrofísica? De esta manera se pretende generar mayores capacidades científicas y tecnologicas como aporte al desarrollo tanto cultural como economico y social de nuestros pueblos. La 1a OAAA en el contexto anterior, constituye un importante estímulo en los estudiantes para el estudio de los astros y las leyes que rigen sus comportamientos.
La 1a OAAA se llevo a cabo, con el exito esperado, a orillas del lago Titikaka, La Paz, Bolivia, del 19 al 23 de Junio de 2009, coincidiendo con el Solsticio de Invierno en el hemisferio Sur. Se conto con la presencia de 4 países: Argentina, Brasil, Bolivia y Mexico. Se tuvieron dos modalidades de evaluacion, Teorica y Practica.
Descriptores: Olimpiadas de Física
Subject headings: Physics Olympiads

En la 1a OAAA se concentraron 35 personas entre estudiantes y profesores, quienes compartieron sus experiencias, costumbres y culturas.
La lista de los ganadores se muestra en la Tabla 1.

¡Felicidades a los países participantes y a todos los jóvenes participantes y ganadores!
A continuacion se presentan los examenes teorico y experimental resueltos, de la 1 ra OAAA.
SOLUCIONES DEL EXAMEN TEÓRICO
1 a Olimpiada Andina de Astronomía y Astrofísica
Lago Titikaka - La Paz - Bolivia, 22 de Junio de 2009
DATOS ÚTILES
Velocidad de la luz: c= 2.99792458x108[m/s]
Masa del protón: mp= 1.6726x10-27 [kg]
Masa del helio: mHe= 6.643x1027 [kg]
Masa del electrón: me= 9.1094x1031 [kg]
Masa del neutrino: mv=0 [kg]
Un electronvoltio:1 eV = 1.6022 x10-19 [J]
Un mega electronvoltio: 1 Mev = 1xl06 [eV]
PREGUNTA 1:
Las estrellas pueden considerarse como cuerpos negros (emisividad ε= 1) cuya superficie emite energía en forma de radiación electromagnética, siguiendo la ley de Stephan-Boltzmann H=AεσT4 , donde H es la corriente de calor debida a la radiación de una superficie A, T es la temperatura absoluta en °K y σ= 5.67 x 10-8 [ Wm-2K-4] es la constante de Stephan-Boltzmann. El Sol tiene una masa aproximada de 1.99x1030[Kg] y una densidad de 2.0 [g/cm3] . Por otra parte, se sabe que en promedio la luz del Sol tarda en llegar a la tierra 8 minutos. Además, sabiendo que la magnitud de Rigel es de 0.34 y la de Proción B es de 13.5 y con toda la información anterior responda las siguientes preguntas:
a) ¿Pueden ambas estrellas verse a simple vista (sin utilizar ningún telescopio)? Justifique su respuesta.
b) Sabiendo que las temperaturas superficiales de Rigel y Proción B son de 1800 [°C] y 9800 [°C] , respectivamente, y que Rigel radia energía a una tasa de 2.7x1032[W] y Proción B a una tasa de 2.1x1023[W] , determine los radios de ambas estrellas. Considere que las estrellas son esféricas.
c) Compare los radios de ambas estrellas con el radio del Sol y con la distancia media Tierra-Sol.
SOLUCIÓN
(a) Sólo Rigel puede verse a simple vista puesto que la magnitud límite estelar en el mejor de los casos alcanza a 6.0, por lo que para observar Proción B se necesita un telescopio.
(b) Para calcular los radios de Rigel (R) y Proción B se utiliza H=AσT4 puesto que ε= 1 .
HR=ARσT4R , donde para calcular AR=4πR2R
HR = 2.7x1032W y Hp=2.1x1023W
Tr = 11073°K y Tp=10073 °K,
de donde:
HR=4πR2RσT4R .
Entonces:
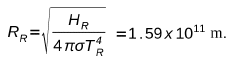
Similarmente:
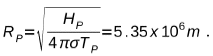
c) Para la comparación con el radio del sol, se debe determinar el mismo a partir de:
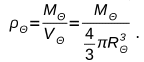
Entonces:

y la distancia media Tierra-Sol se puede calcular a partir de: C= d/t . Entonces, de aquí,
d=Ct= 3x108m/sx480s=1,44x1O11m.
De este modo:
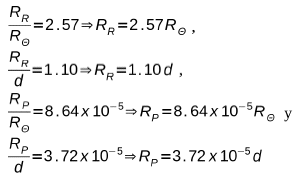
PREGUNTA 2:
En 1938 Hans Albrecht Bethe (1906-2005) en Estados Unidos y Karl Friedrich von Weizsáker (1912-), en Alemania, simultánea e independientemente encontraron el hecho notable de que un grupo de reacciones en las que intervienen el carbono y el nitrógeno como catalizadores constituyen un ciclo, que se repite una y otra vez, mientras dura el hidrógeno. A este grupo de reacciones se las conoce como "ciclo de Bethe o del carbono" (a veces ciclo CNO), y es equivalente a la fusión de cuatro protones en un núcleo de helio. Este ciclo está caracterizado por las siguientes ecuaciones:
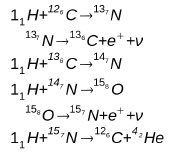
Sumando éstas miembro a miembro se obtiene:
![]()
Como se puede observar, este ciclo es equivalente a la transformación de cuatro protones en un átomo de Helio más dos positrones (antipartícula del electrón, igual masa, pero carga de signo contrario) y más dos neutrinos (necesarios para satisfacer las leyes de conservación de la cantidad de movimiento y del momento angular, aquí se supone que los neutrinos no tienen masa).
Se define a Q, como la diferencia de energía cinética Q=ΔEk del proceso. Mediante operaciones algebraicas se llega a:
![]()
Determine el Q de la ecuación (1) en unidades [Mev] (1 Mev=1x106 [eV] ).
SOLUCIÓN:
Por definición:
![]()
Nuevamente se ha supuesto que la masa del neutrino es cero, lo cual está en entredicho por las últimas investigaciones. Para llevar este resultado a las unidades pedidas, simplemente se utilizan factores de conversión:
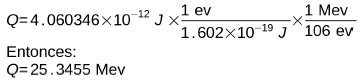
PREGUNTA 3:
La masa del planeta Júpiter es aproximadamente 300 veces mayor que la de la Tierra, por lo que parecería que el peso de un objeto en la superficie de Júpiter fuera 300 veces mayor que su peso en la Tierra. Pero resulta ser que un objeto en la superficie de Júpiter pesa apenas 3 veces más que en la superficie de la Tierra.
a) Dé una explicación de este hecho (guie su razonamiento con ayuda de los términos de la ecuación de fuerza gravitatoria).
b) Estime el diámetro de Júpiter en términos del de la Tierra.
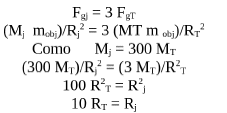
SOLUCIÓN:
a) Al ser la masa mayor, la fuerza gravitatoria (Fig) se incrementa en forma lineal respecto a ésta, pero el radio de Júpiter (j) también es mayor que el de la Tierra T, y como la Fg es inversamente proporcional al cuadrado de este radio, esto hace que el peso de un objeto en la superficie Júpiter sea del mismo orden que su peso en la superficie de la Tierra.
b) Si el peso en Júpiter es aproximadamente 3 veces el de la Tierra T:
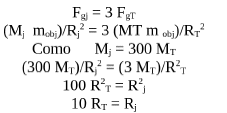
Entonces el R¡ es aproximadamente 10 RT.
PREGUNTA 4:
En las capas más profundas del Sol, simultáneamente con el aumento de la temperatura, debe crecer la presión determinada por el peso de todas las capas suprayacentes. Por lo tanto, la densidad también aumentará. Además de que en cada punto interior del Sol se debe cumplir la denominada condición del equilibrio hidrostático (P=ρgH).
a) Con base en el siguiente esquema:
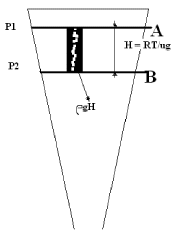
donde:
P1 es la presión en la capa A,
P2 es la presión en la capa B,
ρ es la densidad media entre las capas A y B.
Y con la expresión RT/ug = H0 que tiene unidades de longitud.
Halle la relación aproximada entre las presiones de las capas entre A y B.
Nota.- la mayoría de los objetos astronómicos constan de un gas que se puede considerar perfecto, siendo así, la ecuación fundamental de estado correspondiente es:
P = (ρRT)/u (tomar en cuenta que H0≈H ),
donde: P, es la presión interna del gas; ρ, su densidad; u, la masa molecular relativa, y T la temperatura absoluta del gas expresada en °K; R = 8.31 J/(mol.°K) (considere los valores medios de presión y densidad entre las dos capas).
SOLUCIÓN:
Recordemos que la ecuación de estado es:
![]()
Además también recordemos que la densidad y la presión media entre las capas A y B viene dada por:
![]()
Ahora, remplazando las dos anteriores ecuaciones en (1) tenemos:
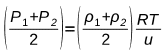
De donde obtenemos:
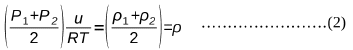
Por otro lado, recordemos que para que se cumpla la denominada condición del equilibrio hidrostático, se tiene que:
![]()
Ahora, remplazando la ecuación (2) en (3):
![]()
Pero recordemos que:
![]()
y además sabemos que H0 = H, con lo que tenemos:
![]()
y con lo que finalmente obtenemos:
P2 = 3P1 que es la relación buscada.
PREGUNTA 5.
Si mal no recuerdo, hace un tiempo en un canal de ciencia se hacia la propaganda de especiales referidos a un gran telescopio en la superficie de la Tierra, y decía algo así: Con este telescopio podrá verse el logotipo de la NASA en el Telescopio Espacial Hubble, si esté se encuentra en órbita circular alrededor de la Tierra a 593 km sobre el nivel del mar, y si suponemos que el logotipo tiene letras de 2 metros de alto. ¿Cuál debería ser el diámetro del telescopio en la superficie?. ¿Cuál es el telescopio, de los que Ud. Conozca, que más se aproxime al cálculo realizado? (Ayuda: utilice la longitud de onda del punto medio del visible, 550 nm).
Respuesta
El poder de resolución de un telescopio es: RP=1/Θmin , donde Θmin es el ángulo mínimo entre dos puntos, y Θmin= 206 265 λ/d, donde λ es la longitud de onda de la luz y d es el diámetro del objetivo. Si consideramos la difracción de una apertura circular, debemos multiplicar este valor por 1.22, entonces para la longitud de onda del visible tenemos:
1.22 x Θmin= 1.22 x 206265 x (5,5 x10-7) / d
1.22 x Θmin= 0.14/d
Ahora, si el telescopio tiene letras de 2 m y está a 593 km, el ángulo que deberíamos poder ver sería
Θ/2 = tan1 (2/593.000)
Θ = 6.74 x 10-6
Luego: d = 0.14/Θ = 0.14 / 6.74 x10-6 = 20.75 m
El telescopio terrestre más grande de la superficie terrestre es el Very Large Telescope, en Atacama, Chile. Se trata de 4 espejos de 8 metros de diámetro. En modo interferométrico, el telescopio tiene una resolución igual a la de un telescopio de un diámetro igual a la distancia entre los espejos, es decir, 100 metros. Con lo que este telescopio fácilmente resolvería este objeto.
PREGUNTA 6. Responda con falso o verdadero:
1. La gran mayoría de las fuentes de rayos gamma consiste de estrellas binarias de Rayos X.
| F | V |
2. La mejor manera de diferenciar si un chubasco atmosférico ha sido generado por un rayo gamma o por una partícula cargada es medir el bajo contenido muónico del mismo (muón=partícula de masa media entre un electrón y un protón).
| F | V |
3. De acuerdo a las teorías actuales, se cree que el Sol existirá tal y como es ahora unos 10.000 millones de años más.
| F | V |
4. Los típicos cúmulos de galaxias pueden tener un diámetro de 107 años luz y contener unas 103 galaxias con un tamaño de 105 años luz separadas por 106 años luz siendo las velocidades típicas galácticas de 103 km/s.
| F | V |
5. Las estrellas que vemos en la vía láctea constituyen parte de un gran disco de estrellas y gas en rotación, que constituyen nuestra galaxia. En la constelación Andrómeda es posible visualizar, con binoculares, a la galaxia espiral llamada Andrómeda o galaxia M31, la cual probablemente se asemeja en su forma a nuestra galaxia si la pudiéramos ver desde lejos. M31 está a 2x106años luz de nosotros.
| F | V |
6. La pérdida de masa solar es de 5 millones de toneladas por segundo.
| F | V |
7. El orden de las Lunas Galileanas, desde el interior y alejándose del planeta Júpiter es: IO, EUROPA, GANÍMEDES, CALIXTO.
| F | V |
SOLUCIÓN DEL EXAMEN EXPERIMENTAL
PARTE I: USE EL PUNTERO LÁSER PROPORCIONADO (15 PUNTOS)
1. Ubique los objetos conocidos como "Corona Austral y Corona Boreal"
2. Dirija el puntero en dirección hacia el Centro de la Galaxia.
3. Mueva el puntero a lo largo de la eclíptica.
4. Dirija el puntero a la estrella llamada Gamma Cruz.
5. En el sur una brillante constelación es el triángulo austral, dirija el puntero a la estrella más brillante del triángulo.
R.- La estrella más brillantes es Alfa Triángulo de magnitud 1.9, trazo espectral BV y a una distancia de 415.5 años luz.
6. Inicie en la estrella Antares (Alfa-Scorpius) en la constelación del escorpión, mueva el puntero 40° hacia al oeste, seguido de 30° hacia el sur (en coordenadas ecuatoriales). Ahora reconozca a la constelación en el campo de visión.
R.- La constelación es VELA
PARTE II: USE LOS BINOCULARES O EL TELESCOPIO (25 PUNTOS)
1. Utilizando el telescopio adecuadamente ubique dos tipos de Cúmulos e indique su nombre.
2. Encuentre la nebulosa laguna (M8).
3. Encuentre un planeta.
4. Utilizando el telescopio adecuadamente ubique dos tipos de Cúmulos o Nebulosas e indique el nombre de los mismos.
Resp.: Cúmulos Globulares: NGC5139 (Omega del Centauro), Centauro, M80 Escorpión, M4-NGC6121 Escorpión. Cúmulos Abiertos: NGC4755 (El Boyero), M6 (Mariposa) Escorpión, M7-NGC6475, Escorpión-Sagitario. Nebulosas: M8 (Nebulosa de la Laguna) Sagitario, M80.
5. Observe las nebulosas laguna (M8) y Trífida (N20) y dibuje su forma y tamaño aproximados que ve a través de los binoculares en el cuadro siguiente con la correcta orientación.














