Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
Compartir
Revista Boliviana de Física
versión On-line ISSN 1562-3823
Revista Boliviana de Física v.15 n.15 La Paz 2009
ARTÍCULO ORIGINAL
ESTUDIO DE LA CORRELACIÓN FOTÓNICA EN LA CAVIDAD RADIANTE UTILIZANDO LA MECÁNICA ESTADÍSTICA NO EXTENSIVA
STUDY OF THE PHOTONIC CORRELATION FOUND IN THE RADIANT CAVITY USING NON EXTENSIVE STATISTICAL MECHANICS
M. J. ANDRADE & M. A. VISCARRA
Carrera de Física
Universidad Mayor de San Simón
Cochabamba - Bolivia
RESUMEN
Este trabajo tiene como objetivo determinar si existe algún grado de correlación entre los fotones de una cavidad radiante utilizando la ley de radiación generalizada obtenida según el formalismo de la Mecánica Estadística No Extensiva. Para tal efecto, se usaron resultados de publicaciones sobre la ley generalizada de la radiación de cuerpo negro, con base a las cuales se estimó un índice entrópico q muy proximo a uno (q = 0.9999), coincidiendo con investigaciones similares. Se realizó la evaluación numérica del modelo generalizado y se lo comparó con el modelo convencional de Planck para dos temperaturas diferentes: 2,75 K (radiación cosmica de fondo) y 5777 K (radiación solar). En el primer caso se vio que para que el modelo generalizado se ajuste mejor a los datos que el modelo de Planck, era necesario un valor de q aún más proximo a la unidad. En el segundo caso, sin embargo, con q = 0.9999 se obtuvo un mejor ajuste que con el modelo de Planck. Esta comparación condujo a dos conclusiones: 1) A temperaturas bajas la correlación fotónica es muy debil o simplemente no existe. 2) A medida que se incrementa la temperatura, podría comenzar a aparecer, levemente, cierta correlación , expresada en un valor de q que difiere cada vez más de la unidad.
Descriptores: mecánica estadística no-extensiva mecánica cuantica estadística termodinámica
Codigo(s) PACS: 05.90.+m, 05.30.d, 05.70.a
ABSTRACT
This study seeks to determine if there exists a correlation between the photons of a radiant cavity using the generalized law of radiation obtained from non extensive statistical mechanics. Results were used from publications on the general radiation law of black body to estimate an entropic index q close to the unit (q= 0.9999). These coincide with similar studies. A numerical evaluation of the generalized model was carried out and compared with the conventional Planck model for two different temperatures: 2,75 K (lower cosmic radiation) and 5777 K (solar radiation). In the first case it was found that the generalized model adjusts better to the data than the Planck model. A value q, even closer to the unit, was needed. In the second case with a value of q = 0.9999 a better adjustment to the data was found compared to the Planck model. The following conclusions were drawn from these results: 1) At lower temperatures the photonic correlation is very weak or non existent. 2) With an increase in temperature a slight correlation expressed by q is seen which differs more each time from the unit.
Subject headings: non-extensive statistical mechanics statistical quantum mechanics thermodynamics
1. INTRODUCCIÓN
La Mecánica Estadística No Extensiva (o de Tsallis), es un intento de generalizar la estadística convencional teniendo a esta última como caso particular. Su principal característica es que presta atención a la correlación existente entre los entes que componen un sistema termodinámico, a diferencia de la estadística convencional en la que se desprecia dicha correlación . Esto puede verse con más claridad si se habla en terminos de la entropía del sistema (Tsallis 1998): si se considera un sistema compuesto por los subsistemas A y B, donde Sq(A) representa la entropía de A y Sq(B) la entropía de B, segun la estadística no extensiva la entropía del sistema compuesto estará dada por:
![]()
donde el último término de la derecha mide el grado de no extensividad ó de correlación, y depende de un índice q conocido como índice entrópico. Para q igual a uno el ultimo termino se anula y la entropía del sistema compuesto es simplemente la suma de las entropías individuales tal como en el caso de la estadística convencional. Pero para valores de q diferentes de uno la no extensividad del sistema se hace evidente, por lo que no se puede despreciar la correlación entre sus componentes. Con base a esta idea Tsallis desarrolló el formalismo de la estadística no extensiva.1
Dado que esta nueva teoría es una estadística más general, tiene como casos especiales a las de Boltzmann-Gibbs, que incluye a las de Bose-Einstein y Fermi-Dirac2, de modo analogo a la teoría de la relatividad que tiene como caso especial a la mecánica newtoniana (Tsallis 1998). Cabe entonces la pregunta de qué forma tendría la ley de radiación en el entorno no extensivo, y que diferencia habría con la ley de Planck. La primera interrogante ya fue abordada en diferentes investigaciones, siguiendo procedimientos diversos pero arribando a resultados similares (Lenzi & Mendes 1998; Martínez et al. 2001; Buyukkilic et al. 2000; Tirnakli & Torres 1999; Chamati et al. 2004). Es la segunda interrogante la que motiva el presente trabajo. Se plantea que la ley de radiación en el marco no extensivo, por tener una forma más general que la ley de Planck, es aún más precisa y se ajusta mejor a los datos experimentales.
En ese sentido, para fines de comparación se va a utilizar la ley de Planck convencional expresada en terminos de frecuencia angular (Huang 1987):
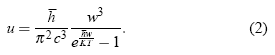
En cuanto a la ley generalizada, se han recopilado los resultados mostrados en la Ec. (3), donde: CT corresponde a la ley de radiación obtenida según el procedimiento de Curado-Tsallis (Lenzi & Mendes 1998), OLM corresponde al procedimiento de los Multiplicadores de Lagrange Optimizados (Martinez et al. 2001), y BE-G corresponde al procedimiento de Bose Einstein generalizado (Buyukkilic et al. 2000). Se sabe que los tres procedimientos mencionados son, matematicamente, equivalentes entre sí (Ferri et al. 2005). Sin embargo, cabe mencionar que los procedimientos CT y OLM son analíticos en tanto que el BE-G viene de una aproximación .
En cuanto a los datos experimentales, se dispone de datos de radiación solar extraterrestre (NASA ) y de radiación cosmica de fondo (MTECH ). La temperatura aceptada en el primer caso es de 5777 K y en el segundo de 2,75 K.

2. METODOLOGÍA
Por razones de computo se ha utilizado el modelo analítico CT y, para la aproximación de partida, el modelo simplificado BEG. De lo que se trata es de hallar el valor de q que mejor represente a los datos experimentales de radiación solar y de radiación cosmica de fondo. Una vez obtenidos los índices, se analiza en qué caso el valor de q se aproxima más a la unidad (si es que fueran diferentes) y se discuten las posibles causas.
El procedimiento detallado fue el siguiente:
i) Sabiendo que el modelo de Planck se ajusta bastante bien a los datos experimentales de radiación solar para una temperatura de 5777 K, se utiliza el modelo BE-G, por su simplicidad, para hallar el índice entrópico q de partida. Como referencia se tiene que |q 1| < 0,0001 (Tirnakli & Torres 1999; Velazquez & Guzman 2001; Tsallis et al. 1995).
ii) Con el índice adoptado q = 0.9999 se procede a evaluar el modelo CT para una temperatura de 5777 K y se lo compara con los datos experimentales de radiación solar. Asimismo, se realiza la contrastación de la ecuación de Planck con los mismos datos experimentales. En ambos casos, se evalúa el grado de ajuste y de esta forma se realiza una primera comparación entre el modelo generalizado y el modelo de Planck.
iii) Para el caso de la radiación cósmica de fondo se sigue el mismo procedimiento que en (ii) pero evaluando en este caso para una temperatura de 2, 75 K.
iv) Observando los resultados de (ii) y (iii) se busca el valor de q que mejor ajuste el modelo CT en comparación con el modelo de Planck. Es decir, se modifica q de manera tal que el modelo generalizado represente a los datos experimentales de mejor manera que el modelo de Planck (si es que fuera posible).
v) Se comparan los índices entrópicos hallados en ambos casos.
3. RESULTADOS
Las curvas de radiación para distintos valores de q según el modelo BE-G se presentan en la Fig. 1.
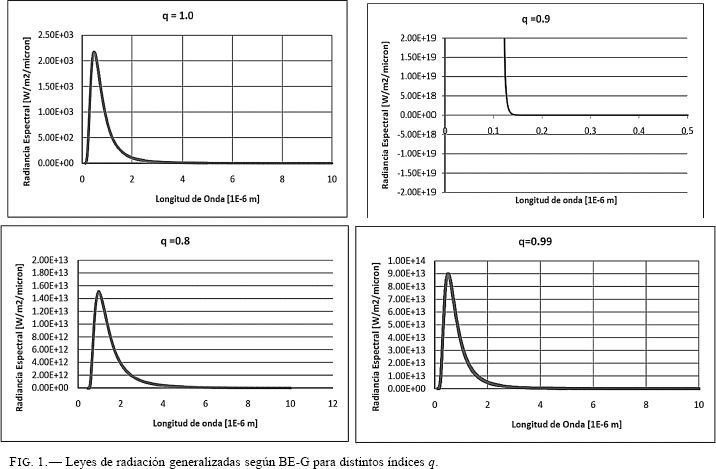
A partir de las gráficas queda claro que el valor de q debe estar entre 0, 9 y 1. Dado que la ley de Planck convencional (q = 1) se ajusta muy bien a los datos experimentales es de esperar que el mejor valor de q sea próximo a ese valor. Para probar esta suposición se ha incluido la curva correspondiente a q = 0,99 observándose una gran discrepancia con q = 1 (en el orden de magnitud) a pesar de haber una diferencia a la centésima en el índice de no extensividad. Esto quiere decir que el valor de q debe ser aún más proximo a la unidad. En ese sentido, y tomando en cuenta las Refs. Tirnakli & Torres 1999; Velazquez & Guzman 2001; Tsallis et al. 1995, se asume como valor de partida q = 0.9999.
El siguiente paso es la contrastación de la ley de Planck con los datos de radiación solar y la contrastación del modelo generalizado CT con los mismos datos experimentales. (Fig. 2).
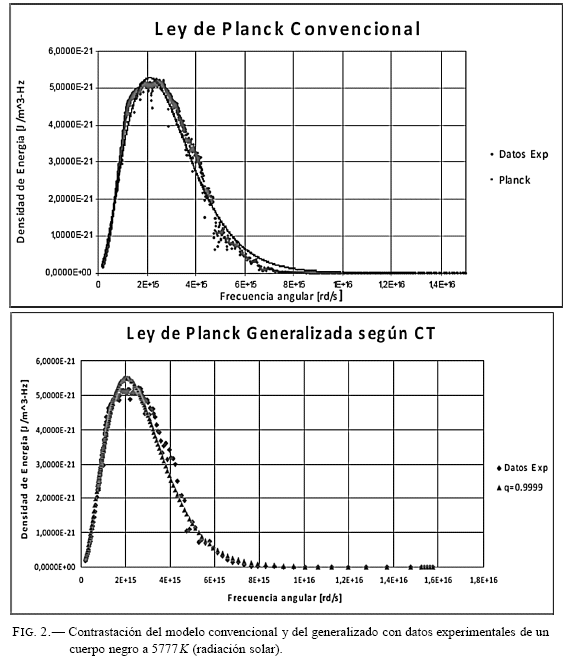
El modelo de Planck presenta una correlación de 99.05% en tanto que el modelo CT una correlación de 99.07%. Ya que el ajuste del modelo generalizado es mejor que el de Planck, no se modifica el valor de q.
Ahora, se repite el procedimiento para la radiación cosmica de fondo (Fig. 3).
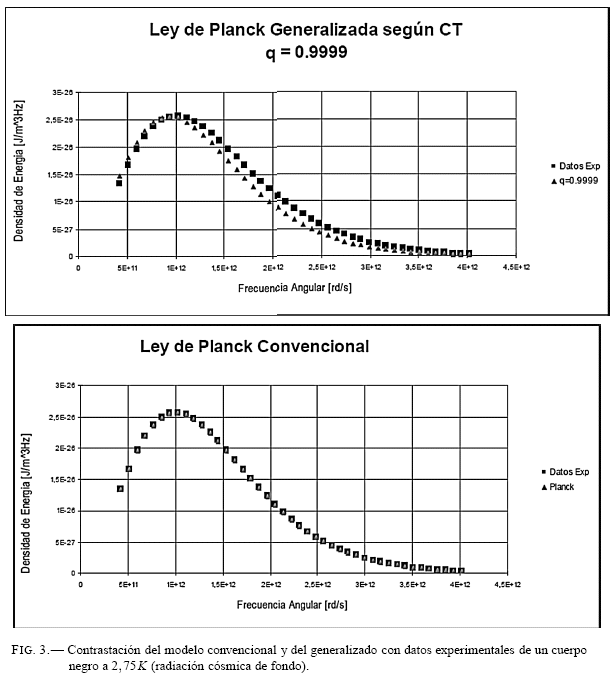
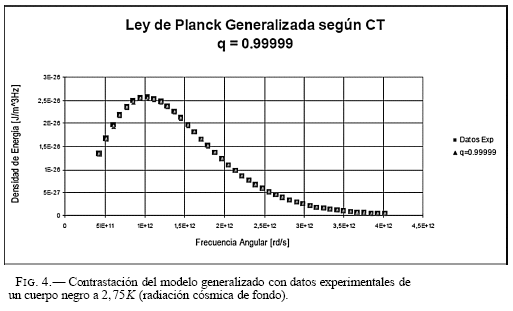
El modelo de Planck presenta una correlación de 99.9996% en tanto que el modelo CT una correlación de 99.3134%. En este caso el ajuste de Planck es superior al del modelo generalizado. En consecuencia se busca un valor de q que mejore el ajuste. Se repitio el calculo con q = 0.99999 y se obtuvo un coeficiente de correlación de 99.9994% que practicamente reproduce el modelo de Planck. (Fig. 4).
4. CONCLUSIONES
Queda claro que para la radiación de cuerpo negro el parametro de no extensividad q debe ser muy proximo a 1, lo que equivale a decir que la interacción fotónica en la cavidad radiante es prácticamente despreciable. Esta es la razón por la que la estadística extensiva obtiene una ley de radiación tan precisa (la ley de Planck convencional). Sin embargo, se ha visto que no hay motivos suficientes para descartar el modelo generalizado con, por ejemplo q = 0,9999, que si bien es muy próximo no es igual a la unidad. Entretanto no se realicen evaluaciones numéricas más finas ni se obtengan datos experimentales en distintas regiones del espectro electromagnetico (ademas de las analizadas en este documento), ambas soluciones podrían considerarse igualmente validas.3
Queda aún la posibilidad de una pequena correlación entre fotones que podría encontrarse en frecuencias mayores al ultravioleta. Esta suposición se basa en los resultados de la comparación del modelo generalizado con los datos experimentales: a bajas temperaturas (2,75 K) la ecuación de Planck se ajusta mejor que el modelo generalizado, pero a mayor temperatura (5777K) el modelo generalizado mejora y su ajuste es ligeramente superior al de Planck. Si esa tendencia se mantiene, se podría esperar que a mayores temperaturas la no extensividad del gas de fotones se hiciera más evidente, lo que implicaría un cierto grado de correlación fotónica expresado en terminos de un índice entrópico q cada vez más alejado de la unidad. Sin embargo, una conclusion definitiva solo podría darse tras comparar el modelo generalizado con un mayor numero de datos experimentales con frecuencias dominantes en el rango de energías altas.
Notas
1 Hablando estrictamente, la Ec. (1) denota no aditividad en lugar de no extensividad. Sin embargo, esta imprecision cometida por Tsallis fue aceptada y en la actualidad le da el nombre a la nueva estadística.
2 Las estadísticas de Bose-Einstein y Fermi-Dirac no son estrictamente estadísticas diferentes, sólo son los mismos conceptos de la estadística de Boltzmann-Gibs aplicados a partículas cuánticas indistinguibles. Las mismas consideraciones que se toman en cuenta sobre la indistinguibilidad de partículas cuánticas, bosones o fermiones, se pueden aplicar al razonamiento de Tsallis llevándonos a la versió n cuántica de la estadística de Tsallis.
3 Nota de los editores: En opinion de uno de los arbitros, la conclusion debería ser que, en este caso, la generalización de Tsallis no se aplica en realidad.
REFERENCIAS
Buyukkilic, F., Sokmen, I., & Demirhan, D. 2000, NONEXTENSIVE THER-MOSTATISTICAL INVESTIGATION OF THE BLACKBODY RADIATION (Faculty of Sciences, Ege University, Turkey) [ Links ]
Chamati, H., Djankova, A., & Tonchev, N. 2004, BLACKBODY RADIATION IN TSALLIS STATISTICS (Institute of Solid State Physics, Sofia-Bulgaria) [ Links ]
Ferri, Martinez, & Plastino. 2005, EQUIVALENCE OF THE FOUR VERSIONS OF TSALLISS STATISTICS (IFLP) [ Links ]
Huang, K. 1987, STATISTICAL MECHANICS (2nd Edition) [ Links ]
Lenzi, E. & Mendes, R. 1998, Physics Letters A, 250, 270 [ Links ]
Martinez, S., Pennini, F., Plastino, A., & Tessone, C. 2001, Physics A, 295, 224 [ Links ]
MTECH. , http://www.mtech.edu/clsps/7Cosmic_Radiation_Background.doc [ Links ]
NASA. , LINEAR PLOT ETR ASTM E-490, ASTM, NASA [ Links ]
Tirnakli, U. & Torres, D. 1999, EXACT AND APPROXIMATE RESULTS OF NON-EXTENSIVE QUANTUM STATISTICS (CBPF, Rio de Janeiro, Brazil) [ Links ]
Tsallis, C. 1998, NONEXTENSIVE STATISTICAL MECHANICS AND THERMODYNAMICS: HISTORICAL BACKGROUND AND PRESENT STATUS (CBPF Rio de Janeiro, Brazil) [ Links ]
Tsallis, C., Barreto, F. S., & Loh, E. 1995, Physical Review E, 52 No. 2 Velazquez, L. & Guzman, F. 2001, MICROCANONICAL THERMOSTATISTICAL INVESTIGATION OF THE BLACKBODY RADIATION (Universidad de Pinar del Rio, Cuba) [ Links ] [ Links ]














