ARTÍCULO ORIGINAL

 

SOBRE UN TIPO DE EFECTO RETICULAR DURANTE LA PROPAGACIÓN LIBRE DE UN ELECTRÓN DE BLOCH

 

A LATTICE EFFECT PRODUCED DURING THE FREE PROPAGATION OF A BLOCH ELECTRON

 

 

DIEGO SANJINÉS C.^†

 

Universidad Mayor de San Andrés, Carrera de Física

c. 27 Cota-Cota, Campus Universitario, Casilla de Correos 8635

La Paz–Bolivia

† Email: sanjines@umsa.edu.bo.

 

---

RESUMEN

Se investiga una de las formas cómo podría maniestarse físicamente la estructura de red periódica en la propagación unidimensional de un electrón de Bloch. Los efectos dinámicos de esta propagación en presencia de ciertos potenciales externos son conocidos: la oscilación de Bloch en presencia de un potencial lineal y localización dinámica en presencia de potenciales armónicos. En ausencia de un potencial externo (propagación “libre”), la teoría semiclásica y la teoría cuántica predicen una velocidad constante de propagación, lo que se verifica en la simulación numérica de la ecuación de Schrödinger. En este caso se puede apreciar que el paquete de ondas gaussiano que simula al electrón en el instante inicial, evoluciona deformándose como una gaussiana asimétrica; si bien el centro de masa (centroide) del paquete se propaga con velocidad constante, el valor máximo del paquete se propaga con una velocidad constante mayor, por lo que se puede concluir que el centro efectivo de interacción eléctrica del paquete se “adelanta” al centro de masa. Se propone un escenario experimental en el que una consecuencia física interesante (y eventualmente medible) de dicho “adelanto” se manifiesta en un cristal ideal en 2D.

Descriptores: teoría de transporte electrónico — fenómenos de conductividad — transporte por “hopping”

Código(s) PACS: 72.10.Bg, 72.20.-i, 72.20.Ee

---

ABSTRACT

A study is carried out of an effect due to the structure of the lattice in the propagation of a one-dimensional Bloch electron. The dynamics of this propagation in the presence of certain external potentials are well known: the Bloch oscillation in the presence of a lineal potential and the dynamic localization in the presence of harmonic potentials. In the absence of an external potential (free propagation), both the semi classic theory and the quantum theory predict a constant propagation velocity which is verified by numerical simulations of the Schrdinger equation. In this case, the Gaussian wavepacket that simulates the electron in its initial state, evolves itself into an asymmetrical gaussian maintaining the centre of mass at a constant velocity. However the wavepackets peak propagates with greater velocity, indicating that the center of mass lags behind the effective center of the electrical interaction. We propose an experimental scenario in which an interesting physical consequence of such a lag would manifest itself in an ideal 2D crystal.

Subject headings: electronic transport theory — conductivity phenomena — “hopping” transport

---

 

 

1. INTRODUCCIÓN

La evolución de un paquete de ondas cuántico que representa a un electrón moviéndose en presencia de la estructura periódica de la red en una dimensión (1D) se estudia usualmente a través de la correspondiente ecuación de Schrödinger dependiente del tiempo

con un hamiltoniano de enlace fuerte o tight-binding (ver, por ejemplo, Ashcroft and Mermin 1976, cap. 10) dado por H(, )= −2Acosα+ V(), donde: V ()= V (x) es un potencial arbitrario externo que no es intrínseco a la red, A es una integral de solapamiento entre sitios reticulares vecinos (o elemento de hopping, Madelung 1978) y = −ih∂_x. Este será pues el modelo físico al que nos referiremos como “electrón de Bloch”; el fenómeno de la oscilación de Bloch se verifica cuando el potencial externo corresponde a un campo eléctrico externo estático y homogéneo, i.e., V(x) α x (la referencia histórica canónica es Bloch 1928)¹.

La solución de la ecuación de Schrödinger (1), la función de onda Ψ, se puede representar en la base de funciones de Wannier Φ (definida en la red 1D) como

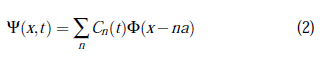
donde las Φ(x −na) están fuertemente centradas en torno al sitio n (con n entero) de una red de Bravais con constante de red a que representa geométricamente al cristal en 1D. Los coeficientes C_n(t) indican de manera efectiva cuál es la dinámica del paquete de ondas a medida que se propaga por el cristal, pues la densidad de probabilidad cuántica |Ψ|² está representada por |C_n|². La ecuación iterativa de evolución temporal para C_n(t) que resulta de sustituir (2) en la ecuación de Schrödinger y discretizar al tiempo como t = pΔt (p = 0, 1, 2,... ) es

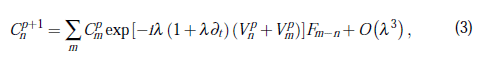
donde λ ≡ Δt/2,   ∂_tV_m^p    = ∂_tV(x = ma, t = pΔt ) y

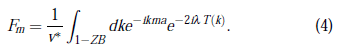
En (4) T(k) es la energía cinética de enlace fuerte dada por T(k)= −2A cos(ka); la integral sobre k se efectúa en la primera zona de Brillouin (1-ZB) y luego se divide por el volumen v* de la 1-ZB. El esquema dado por la aplicación de las ecuaciones (2)—(4) a problemas de dinámica de partículas en una red resulta de adaptar el formalismo del método pseudo-espectral al tipo de banda de enlace fuerte T(k) referida arriba (Sanjinés 2001).

La solución de (3) para el caso de la evolución libre (V(x) = 0) del paquete de ondas (ver (7) abajo) servirá —entre otros— para calcular el centroide del paquete de acuerdo a (n) ≡ Σ_n|C_n|²n. Esta cantidad, junto a la posición cuadrática media (n²), constituyen las principales variables dinámicas en el estudio de la oscilación de Bloch y sus fenómenos asociados, como ser localización dinámica (Dunlap and Kenkre 1986) . En este trabajo se utilizará, además de (n), la cantidad (n³)que está asociada al concepto de asimetría o “sesgo” (skewness) de una distribución de probabilidad (Freund and Wanpole 1980). La eventual aplicación física sugerida en este trabajo (sección 5) para dicho sesgo es un tema que —hasta donde se pudo constatar— no está referido en la literatura usual sobre la dinámica de paquetes de onda en una red.

 

2. PROPAGACIÓN ASIMÉTRICA DEL PAQUETE INICIAL GAUSSIANO

En este artículo nos interesa investigar cómo se comporta un paquete inicial gaussiano (normalizado) dado por C^_n0 = Bexp(−n²/σ) exp(ikan) con B = (2/πσ)^1/4 y con velocidad inicial v(0) α senk cuando se propaga en ausencia de algún potencial externo V(x); en tal caso aún la interacción del paquete con la red se efectúa por medio de la energía cinética de enlace fuerte T(k). A este tipo de dinámica es a lo que nos referiremos como “propagación libre en la red”, en contraste con la propagación libre en el contínuo, donde la energía cinética es h²k²/2m con el resultado bien conocido de un paquete gaussiano que se va dispersando simétricamente en torno a su centroide, el que a su vez se propaga con velocidad constante (ver, por ejemplo, Liboff 1980, cap. 6). Lo interesante del problema abordado aquí es que, si bien el paquete en la red así como el paquete en el continuo se propagan con velocidad constante, el paquete en la red no se dispersa de manera simétrica en torno a su centroide. Debe señalarse que este es un resultado estrictamente cuántico, ya que la aplicación de las ecuaciones de movimiento semiclásicas (Ashcroft and Mermin 1976, cap. 12) al hamiltoniano de enlace fuerte no podrá revelar tal dispersión asimétrica.

En ausencia de un potencial externo (V(x)= 0) la ec. (3) se “integra” en el tiempo y resulta en

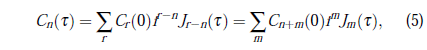
donde se definió el “tiempo adimensional” τ ≡ 2At. (Ya que tomaremos h = 1 a lo largo de este trabajo, entonces el elemento de hopping A se mide en unidades de tiempo inverso s⁻¹). Para el paquete inicial gaussiano C_r(0)=C_r⁰ referido arriba, y para las funciones de Bessel expresadas en su representación integral como

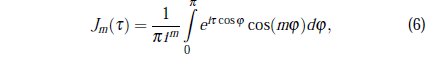
se obtiene de (5) los coeficientes

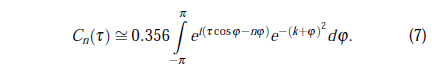
Para llegar a (7) se tomó una constante de red unitaria α = 1 y una desviación estándar σ = 4 en el paquete inicial C_r(0). Debemos señalar que la elección particular que hacemos de constantes y parámetros físicos tiene por finalidad poder expresar de la manera más sencilla posible las expresiones que, como (7), revelarán los aspectos cualitativos más importantes de la dinámica de la propagación libre del electrón de Bloch, que en este trabajo se resumen en la propagación asimétrica del paquete de ondas que representa a la partícula en cuestión. Por esta misma razón, omitiremos en adelante el coeficiente 0.365 en (7).

En la Fig. 1 se aprecia la secuencia evolutiva de densidades de probabilidad |C_n|² para una velocidad inicial v(0) α senk con k = 1. Los perfiles de dicha densidad corresponden (de izquierda a derecha) a los instantes adimensionales τ = 0, 20, 40, 60, 80, 100, 120, 140, 160.

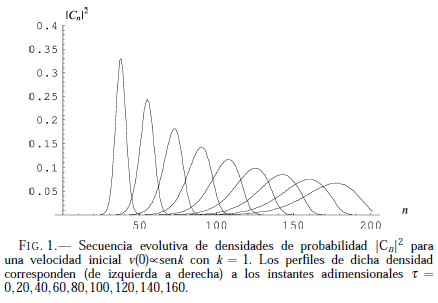
En esta secuencia evolutiva ya podemos apreciar, como se anunció, que la propagación libre en la red del paquete inicial corresponde a una gaussiana asimétrica. A fin de caracterizar analíticamente a cualquier gaussiana asimétrica de la Fig. 1 será necesario utilizar un modelo adecuado para tal efecto. De hecho, existen varios modelos y aplicaciones de gaussianas asimétricas² de las que destacan aquellas que se construyen “pegando” dos mitades de gaussianas ordinarias con diferentes desviaciones estándar; no obstante, para los fines de este trabajo, será mejor considerar un modelo de gaussiana asimétrica definida sobre todo su dominio con los mismos parámetros.

La expresión para C_n(τ) en (7) es una integral que no se puede resolver de una forma analítica sencilla y compacta. Lo ideal —en el contexto de este trabajo— sería ciertamente resolver (7) analíticamente; sin embargo, ya que es posible obtener la expresión cuántica exacta para la velocidad del centroide del paquete de ondas, entonces en realidad sólo nos interesa conocer la velocidad con que el máximo del paquete se adelanta al centroide. A partir de un modelo de gaussiana asimétrica que ajustaremos empíricamente según la simulación de la Fig. 1, se podrá calcular entonces la posición del centro efectivo de interacción eléctrica asociado al sesgo del paquete de ondas. El criterio utilizado para lograr lo anterior es simple: la contribución significativa para |C_n|² proviene de los sitios en donde el integrando de C_n(t) en (7) oscila menos. Para lograr dicha condición utilizaremos el criterio dado por

Definiendo la variable auxiliar ξ como

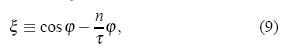
se tiene pues que la condición dada en (8) sólo se cumple si

donde p es un entero y el tiempo adimensional τ puede considerarse —sin pérdida de generalidad— como un número natural (incluyendo al cero) que, para un cierto instante arbitrario después del instante inicial τ = 0, podría llegar a ser un número suficientemente grande. Así, la condición (8) se cumple cuando

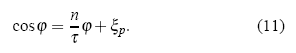
Esta es una ecuación trascendental cuyas soluciones para φ se pueden estimar gráficamente en la Fig. 2, donde se incluye la gaussiana dada en el integrando de (7). Así, la soluciones de (11) corresponden a los valores de φ para los cuales el conjunto de líneas rectas de pendiente n/τ interseca a la curva cosφ. Esta intersección puede ser de dos formas: la línea recta es secante a cosφ, o bien, la línea recta es tangente a cosφ.

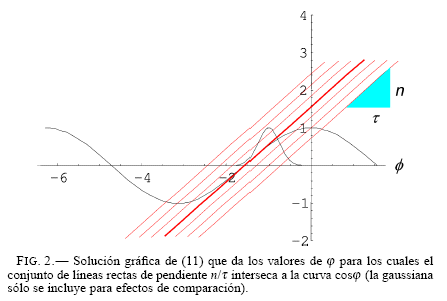
Así, las regiones de intersección donde la tangente a la curva tiene la pendiente n/τ definen uno o varios conjuntos “densos” de soluciones para φ tales que se cumple la condición (8) y por lo tanto el integrando en (7) oscila poco. ^´

Estos son los casos que nos interesan pues contribuyen de manera más significativa al valor final de la integral (7). Los demás casos corresponden a una oscilación rápida del integrando en (7) lo que provoca que el valor de la magnitud de C_n(t) sea relativamente pequeño. El conjunto de rectas de pendiente n/τ puede ser denso, pues la separación sobre el eje vertical de dos rectas adyacentes es ξ_p+1− ξ_p = p/τ ; ya que τ puede ser muy grande, entonces dicha separación podrá ser muy pequeña. En consecuencia, para valores de la pendiente n/τ ≤1 siempre habrá rectas que sean tangentes a cosφ en algún punto. En la Fig. 2 se muestra algunas rectas, de las que la que tiene el trazo grueso es tangente a cosφ en φ = − π/2.

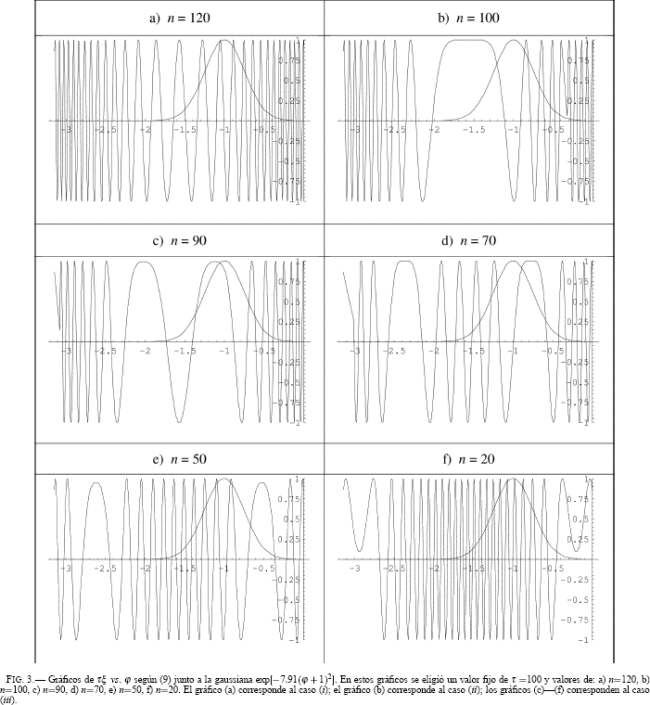
Distingamos pues los casos siguientes correspondientes a la condición (8):

i) n > τ → no hay zonas “densas”; oscilación rápida del integrando en (7).

ii) n = τ → hay una gran zona “densa”; régimen estacionario del integrando en (7).

iii) n < τ → hay varias zonas “densas” más pequeñas régimen estacionario del integrando en (7).

Ilustremos estos casos con los gráficos de la Fig. 3 donde se graficó τξ vs. φ según (9) junto a la gaussiana exp[−7.91(φ + 1)²]. En estos gráficos se eligió un valor fijo de τ =100 y valores de: a) n=120, b) n=100, c) n=90, d) n=70, e) n=50, f) n=20. El gráfico (a) corresponde al caso (i); el gráfico (b) corresponde al caso (ii); los gráficos (c)—(f) corresponden al caso (iii).

Los anteriores gráficos revelan la forma cómo los parámetros n y τ se deben relacionar a fin de contribuir de manera significativa a C_n(t) en (7). Es más: la relación entre n y τ según los casos (i), (ii) o (iii) permite prever que el perfil de la densidad de probabilidad |C_n|² presentará una asimetría con respecto al “centroide” del paquete, tal como se observa claramente en las gaussianas asimétricas de la Fig. 1.

 

3. ADELANTO DEL CENTRO EFECTIVO DE CARGA ELÉCTRICA CON RESPECTO AL CENTRO DE MASA

En la Fig. 4 se graficó la evolución temporal del centroide (n) ≡ Σ_nn|C_n|² y del punto máximo n_m correspondientes a cada una de las gaussianas asimétricas en la secuencia de la Fig. 1.

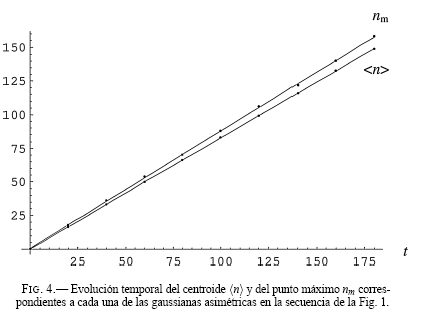
Recordemos que el cálculo exacto para el ritmo de variación en la posición del centroide (n) corresponde a su velocidad inicial v(0) (Sanjinés 2001), pues esta se mantiene constante siempre que la evolución sea “libre” (i.e., V(x)= 0):

Tomando 2A=1, |S₀|=0.986 y ka=1 se obtiene una velocidad inicial v(0)=0.829, lo que coincide razonablemente con el valor que se desprende de la simulación numérica de la Fig. 4 (el error porcentual es de 0.12%):

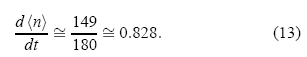
Por otra parte, para n_m se calcula su ritmo de variación a partir de la simulación:

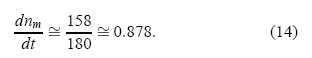
Observando la solución gráfica de la Fig. 2 tenemos que

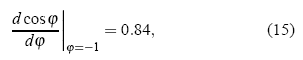
por lo que la contribución más importante a C_n(t) proviene de la región n/τ Є [0.84, 1]. Esto es ciertamente muy razonable en vista de la serie de gráficos de la Fig. 3.

A continuación se deducirá de una manera semi-analítica la expresión que permita calcular el adelanto de n_m, el punto máximo de la gaussiana asimétrica, con respecto a su centroide (o centro de masa) (n). El objetivo que se persigue es poder estimar a partir de este cálculo, cuál sería el sitio efectivo de un paquete de ondas electrónico desde el cual se “emite” el campo eléctrico, es decir, el “centro efectivo de interacción eléctrica” cuya posición será identificada como n_q. Ya que la densidad lineal de carga eléctrica asociada a un paquete de ondas es λ(x)=q|Ψ|², con q = -e la carga del electrón (y |Ψ|²=|C_n|²), entonces se debería esperar que n_q se encuentre próximo a n_m, pues es sabido que el campo eléctrico es más intenso allí donde la densidad de carga eléctrica es mayor. De hecho, en vista del adelanto de n_m respecto a (n), ya se puede inferir al menos que n_q > (n).

En la Fig. 5 se muestra el detalle ampliado de la Fig. 2 donde la recta tangente a la curva cosφ permite estimar un intervalo centrado en φ₀ de magnitud 2Δφ.

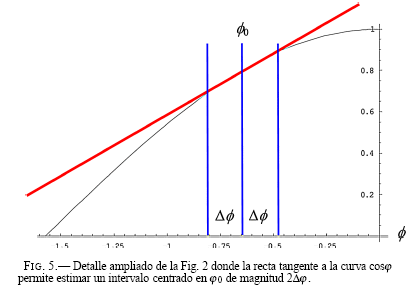
Este intervalo es aquel que en los gráficos de la Fig. 3 corresponde a los sitios donde la función oscilatoria en el integrando de (7) oscila menos, y por lo tanto permite tener una estimación aproximada de la región efectiva produce la mayor contribución a la amplitud de probabilidad C_n.

Desarrollando cosφ en serie en torno a φ₀ hasta el término de orden 2, se obtiene Δφ=|φ−φ₀|= γtanφ₀, (con γ<1). Así, ya que la pendiente de la recta tangente en φ=φ₀ es n/τ, la condición dada por

permite tener una estimación aproximada de la región efectiva donde el integrando de (7) contribuye de forma significativa a la integral correspondiente para C_n(τ). De acuerdo a la evidencia numérica dada por las simulaciones de la Fig. 3, el valor adecuado de γ en (16) será γ= 1/2. De aquí, C_n(τ) en (7) se podrá aproximar por

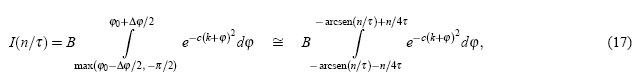
donde c 7.91, k=1y B es una constante apropiada que comprende a la constante de normalización.

Al aproximar C_n(τ) I(n/τ) se debe tomar en cuenta que, formalmente, para un valor fijo del tiempo adimensional τ, la posición n de cada átomo puede tomar los valores correspondientes a un cristal unidimensional infinito, i.e., −∞ ≤ n ≤∞, por lo que la nueva variable independiente n/τ de I(n/τ) tomará los valores −∞ ≤ n/τ ≤∞. Esto naturalmente introduce una indefinición en los valores de n en I(n/τ), por lo que en general se podrá escribir C_n(τ) I((n+m)/τ) donde m es un entero arbitrario, o bien, C_n+m(τ) I(n/τ). Por otra parte, y solamente como consecuencia del método semi-analítico de aproximación que conduce a (17), debe tomarse n/τ ≤ 1 en los límites de integración, para lo que será suficiente considerar sólo 0 ≤ n/τ ≤ 1, pues fuera de este intervalo la integral en (17) es prácticamente nula. Las consideraciones hechas en este párrafo pueden verificarse, por ejemplo, al comparar en la Fig. 6 los perfiles de densidad de probabilidad |C_n+m(τ)|² |I(n/τ)|²=0.228, con m=22 y B 0.228 correspondientes al instante τ =160.

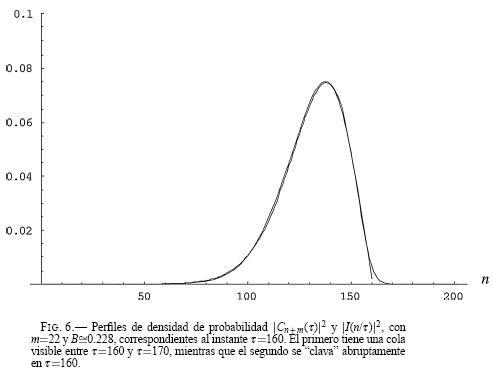
De hecho, la aproximación de los gráficos de la Fig. 6 es tan buena, que apenas se puede distinguir los perfiles de |C_n+m(τ)|² y de |I(n/τ)|²: el primero tiene una cola visible entre τ=160 y τ=170, mientras que el segundo se “clava” abruptamente en τ=160. Para otros valores de τ la aproximación también es muy buena, manteniéndose el valor de m=22, pero ajustando los valores de la constante B para cada valor específico de τ. (Como veremos luego, el valor de B resultará inmaterial para efectos de calcular el adelanto de n_m y n_q respecto a (n).)

A continuación deduciremos, de acuerdo a (17), la expresión que permitirá calcular la velocidad de adelanto de n_m. Para ello reescribamos (17) definiendo las variables auxiliares z ≡ n/τ, φ₁ ≡ −arcsen z − z/4, φ₂ ≡ −arcsen z + z/4, u ≡ (φ + k), u_i (φ_i + k) (i = 1, 2). Así, I(z) en (17) queda como

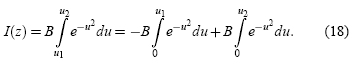
El punto máximo n_m del paquete gaussiano asimétrico se halla pues de acuerdo a la condición ∂_z|I(z)|²=0, lo que se traduce en exp(−u_1²)∂_zu₁(z)= exp(−u_2²)∂_zu₂(z), que a su vez, después de algunas manipulaciones algebraicas, se transforma en una ecuación algebraico-trascendental para z:

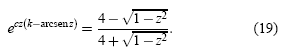
Resolviendo numéricamente (19) para c 7.91 y k=1, se obtiene

lo que coincide razonablemente bien con el resultado (14) de la simulación numérica representada en la Fig. 4 (el error porcentual es de 1.9%). Comparando (14) y (20) se verifica que ∂_τn_m = n_m/τ, i.e., el punto máximo n_m del paquete gaussiano asimétrico se propaga, adelante del centroide (n), con velocidad constante.

 

4. POSICIÓN DEL CENTRO EFECTIVO DE INTERACCIÓN ELÉCTRICA

A continuación calcularemos la posición del centro efectivo de interacción eléctrica n_q a partir del potencial electrostático V(x,y) (la variable definida arriba como z = n/τ correspondería pues a una posición estática para un cierto instante adimensional τ); de aquí se calculará el campo eléctrico E(x, y) que se mediría en el punto (x, y) a causa de una distribución de carga unidimensional λ(z)=q|Ψ(z)|² (con q=–e la carga del electrón y |Ψ|²=|C_n|²). El potencial electrostático asociado a esta distribución de carga es

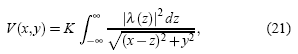
donde K ≡ 1/(4πε₀). Ya que E=–V en 2D, las derivadas respecto a las coordenadas x, y se pueden obtener derivando el integrando en (21), pues las coordenadas son independientes de la variable de integración z. Así, las componentes de E a lo largo de un punto sobre el eje Y (x=0) resultan ser:

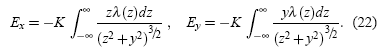
Ahora supongamos que dicho punto se encuentra a una distancia y por encima del eje X mucho mayor que el tamaño “efectivo” del paquete de ondas, de tal manera que y » z en las integrales de (22). En tal caso, obviamente la variable z no alcanzaría a tomar valores muy grandes pues el paquete de ondas está localizado dentro de un intervalo finito y la variable y siempre se puede tomar mucho mayor que los límites de dicho intervalo. Esta consideración nos permite desarrollar los integrandos de (22) en serie y luego proceder a realizar las integrales. Así, sustituyendo

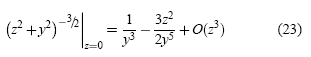
en (22) se obtiene:

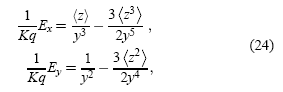
donde (zⁿ) ≡ ∫zⁿ|Ψ(z)|² dz para n = 0, 1, 2, 3. En el caso n=0 se obtiene z= 1 pues el paquete está normalizado.

Si ubicamos al paquete de ondas (distribución de carga) sobre el eje X de tal forma que su centroide (n) coincida con el origen del eje X, entonces (z)= 0. A continuación definamos d ≡ y|E_x/E_y| como la posición del centro efectivo de interacción eléctrica n_q con respecto al centroide del paquete, es decir, d=n_q−(n). Así entonces, de (24) se tiene que

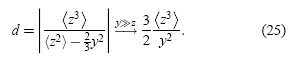
El numerador de d en (25) se reconoce como el sesgo de una distribución de probabilidad(Freundand Wanpole 1980).Ya que en este trabajo dichas distribuciones o paquetes de onda son gaussianas asimétricas, entonces la distancia d es una medida de dicho sesgo. En efecto, para el paquete inicial que es gaussiano, el sesgo es cero y por lo tanto d=0, lo que significa que el centro efectivo de interacción eléctrica n_q y el centro de masa (n) coinciden, pero a medida que el paquete “avanza”, n_q se adelanta a (n) por una distancia d que crece a medida que el paquete se hace más asimétrico, i.e., a medida que el sesgo aumenta. Nótese que dada la aproximación (23) para y » z, el término dominante de E_y en (25) es Kq/y² ley de Coulomb), así que el denominador en (25) no puede ser cero.

 

5. UN EXPERIMENTO PENSADO

La Fig. 7 ilustra un posible escenario experimental que permitiría —en principio— observar un fenómeno muy interesante asociado al adelanto del centro efectivo de interacción eléctrica con respecto al centro de masa.

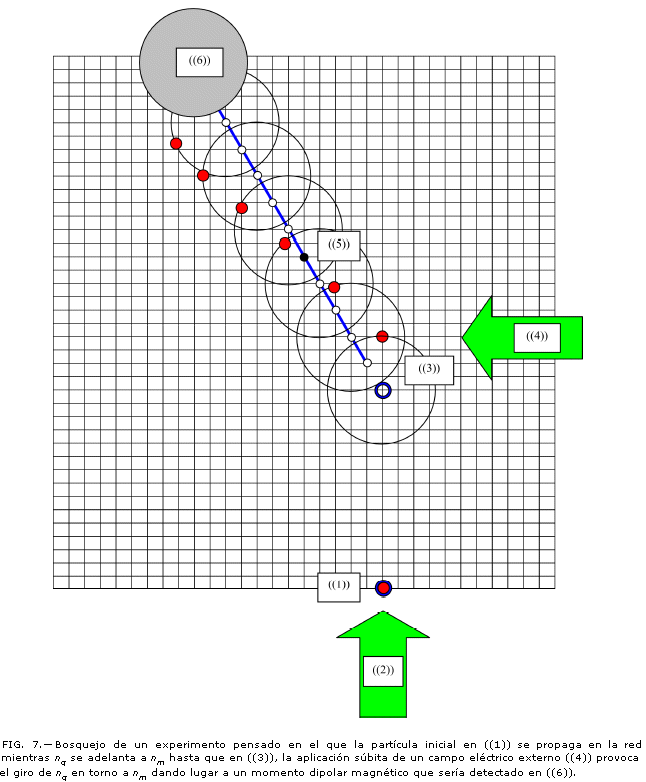
Supongamos un cristal 2D ideal en el que se inyecta un electrón ((1)) y se le da un impulso ((2)) inicial a través de un campo eléctrico muy intenso pero muy breve (a la manera de una delta de Dirac). A partir de este instante, el electrón se propaga libremente mientras su centro efectivo de interacción eléctrica —n_q— se va adelantando al centro de masa —n_m— ((3)). En un cierto instante posterior, se aplica de nuevo un impulso tipo delta ((4)) que actúa sobre n_q, lo que provoca la aparición de un momento angular de n_q en torno a n_m que se propaga en una nueva dirección del cristal 2D. Dicho momento angular daría lugar a un momento dipolar magnético orientado en la dirección perpendicular al plano del cristal. Si en la posición ((5)) se halla una impureza, el paquete de ondas se dispersaría significativamente sólo si las posiciones de n_q y de la impureza coinciden exactamente, en cuyo caso el dipolo magnético se debilitará significativamente (si no se destruye del todo); de otro modo, el paquete probablemente no se disperse mucho y se mantenga el dipolo. Así, en el caso del debilitamiento del dipolo, el solenoide ((6)) no detectaría una mayor variación del flujo magnético, pero si el paquete no fue dispersado por la impureza, entonces el solenoide detectará el campo magnético del dipolo.

 

6. EL PROBLEMA EN 2D

El experimento pensado descrito en la sección anterior naturalmente se podría estudiar desde un principio como un problema dinámico en 2D. La forma más general de extender (3) a un número de dimensiones 3N (con N un número natural) es (Sanjinés 2001)

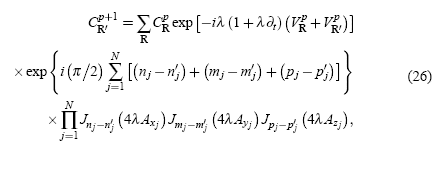
donde los índices R y R^′ se suman sobre toda la red de Bravais. Asimismo se puede obtener de manera directa el caso correspondiente a una red en 2D con celda unitaria cuadrada (constante de red α=1 en las direcciones de X y Y):

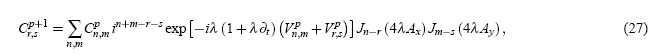
cuya aplicación se puede simplificar aún considerando una red isotrópica (A_x = A_y = A). Esta fórmula constituirá el punto de partida de la investigación sobre la dinámica del paquete gaussiano en 2D. Es importante señalar que si bien la evolución es “libre” (V(x,y)=0) antes y después del instante indicado por ((4)) en la Fig. 7, la variación temporal de V(x,y) en dicho instante es muy grande, pues corresponde a un “pulso” del campo eléctrico externo que desviará al paquete de ondas hacia otra dirección. Tal variación de V(x,y) estará pues ya incorporada en la evolución temporal del paquete expresada por (27), por lo que cabría esperar alguna evidencia más sólida que revele el fenómeno predicho en este trabajo: la rotación de una carga eléctrica en torno al centro de masa del paquete y la subsecuente formación de un momento dipolar magnético.

 

7. PERSPECTIVAS

Así como las ondas planas exp(ikx) son las eigenfunciones del hamiltoniano ²/2m para la partícula libre en el contínuo, las funciones de Bloch exp(ikx)u(x) son las eigenfunciones del hamiltoniano de enlace fuerte −2Acosα para la partícula “libre” en la red, con u(x+α)=u(x). Además, ya que tanto las ondas planas como las funciones de Bloch forman conjuntos completos de funciones (Ashcroft and Mermin 1976, cap. 10), entonces un paquete de ondas —como ser el paquete gaussiano— se puede representar como una integral sobre dichas funciones multiplicadas por factores de peso (o amplitudes de probabilidad de momentum) que, en el caso del contínuo, se sabe que también corresponde a una distribución gaussiana (Liboff 1980, cap. 6). De esta forma es posible entender la causa de la evolución típica de un paquete de ondas gaussiano en el contínuo: la deformación simétrica de este paquete se debe a la propagación también simétrica de sus componentes exp(±i|k|x) cuya amplitud de probabilidad de momentum es la misma.

En el caso de la red, cabe preguntarse asimismo cual será la correspondiente amplitud de probabilidad de momentum que, en el caso de no ser simétrica como en el contínuo, podría explicar por qué las componentes exp(±i|k|x)u(x) con la misma magnitud de velocidad de fase deforman al paquete de una manera asimétrica. Esta especulación será motivo de una investigación posterior.

Por otra parte, en un próximo trabajo se implementará numéricamente el algortimo dado por (27) a fin de investigar el comportamiento dinámico del paquete gaussiano en el caso del experimento pensado en 2D referido arriba. Se investigará sobre la cuestiónde la validez del hamiltoniano de enlace fuerte correspondiente a una banda H(, )= −2Acosα+V() en el preciso instante ((4))de la variación súbita de V(x). Igualmente, en dicho trabajo anunciado se conservará las unidades físicas de las constantes y parámetros relevantes a fin de lograr alguna estimación numérica de la magnitud del momento dipolar magnético referido arriba comparado, por ejemplo, con el magnetón de Bohr.

 

AGRADECIMIENTOS

Agradezco la cordial invitación del Dr. Pedro Pereyra (Grupo de Física Teórica de la Universidad Autónoma Metropolitana-A; México, DF) con quien tuve la oportunidad de intercambiar puntos de vista sobre el tema de este trabajo y otros temas relacionados. Asimismo agradezco el interés del Dr. César Flores (Instituto de Alta Investigación de la Universidad Tarapacá de Arica, Chile) quien en reciente visita me ofreció sugerencias útiles para mejorar y ampliar este trabajo.

 

APÉNDICE
A.

Si bien (18) ya es una expresión analítica para I(z), la dependencia relevante de z se encuentra en los límites de integración de I(z), lo que puede no ser muy práctico a efectos de su tratamiento analítico (por ejemplo, para integrarse). Así, en este trabajo proporcionamos otra forma analítica aproximada para I(z) que se obtiene de la definición de la función error (o integral de probabilidad, Abramowitz and Stegun 1965), usando las mismas variables definidas para (18):

donde además se definió

junto con

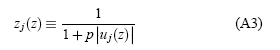
y las constantes p=0.32759, α₁=0.25482, α₂=–0.28449, α₃=1.42141, α₄=–1.45315, α₅=1.06140. Aún en las ecs. (A1)—(A3) la variable z está restringida al intervalo 0 ≤ z ≤ 1. Aunque (A1) ofrece un tratamiento analítico relativamente más cómodo, la función discontinua sgn(ui) puede resultar inconveniente. Por ello, ofrecemos aun otra forma analítica para I(z) donde la variable z ya se puede extender a todos los reales, −∞ ≤ z ≤∞:

Si graficamos la densidad de probabilidad |I(z)|² según (A1) con B=1 y la comparamos con |I(z)|² según (A4) con B= wwww, obtenemos esencialmente el mismo carácter cualitativo que se observa en la Fig. 6.

 

NOTAS

¹ Una introducción pedagógica a la dinámica de las oscilaciones de Bloch en 1D se da en Hartmann et al. (2004) , cuya lista de referencias constituye además una excelente fuente de información actualizada que resume el trabajo de otros investigadores y provee una visión global de estos temas de investigación.

² Ver, por ejemplo, The Skew-Normal Probability Distribution, http://www.iop.org/˜/njp4 1 002.html, y referencias allí citadas.

 

REFERENCIAS

N. Ashcroft and N. Mermin, Solid State Physics (Saunders College, 1976).         [ Links ]

O. Madelung, Introduction to Solid State Theory (Springer, 1978).         [ Links ]

F. Bloch, Z. Physik 52, 555 (1928).         [ Links ]

T. Hartmann et al., New Journal of Physics 6, 2 (2004).         [ Links ]

D. Sanjinés, Tesis doctoral (Universidad Simón Bolívar, Caracas, Venezuela, 2001).         [ Links ]

D. H. Dunlap and V. M. Kenkre, Phys. Rev. B 34, 3625 (1986).         [ Links ]

J. Freund and R. Wanpole, Mathematical Statistics (Prentice-Hall, 1980).         [ Links ]

R. Liboff, Introductory Quantum Mechanics (Holden-Day, 1980).         [ Links ]

M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions (Dover, 1965).         [ Links ]

D. Sanjinés and J.-P. Gallinar, Phys. Rev. B 64, 054301 (2001).         [ Links ]