MODELO MONTE CARLO PARA IRRADIANCIA RELATIVA UV-B

V. M. Peñafiel¹

Carrera de Física, FCPN (UMSA)
La Paz, Bolivia

---

RESUMEN

Se ha logrado modelar el perfil de irradiancia solar ultravioleta usando el método Monte Carlo como simulador de la dispersión de fotones en una atmósfera esférica y homogénea. Hipotéticamente, se considera que la irradiancia relativa (adimensional y normalizada a la unidad) está asociada principalmente a la dispersión de Rayleigh y a la geometría atmosférica en tanto que la magnitud irradiativa requeriría un tratamiento más detallado (y la inclusión de otros fenómenos, como la absorción de fotones).

Se detalla el fundamento teórico usado para los algoritmos de cómputo, los cuales son lo suficientemente flexibles como para permitir "experimentos" con variación de los parámetros principales; incluyendo también una atmósfera exponencial, orientada, sobre todo, al análisis comparativo.

Descriptores: método Monte Carlo — simulación computacional — física de la atmósfera

---

ABSTRACT

A simulation of the ultraviolet solar irradiance profile, studying the dispersion of photons in a spherical and homogeneous atmosphere, was realized using the Monte Carlo method. Hypothetically, relative irradiance (dimensionless and normalized to the unit) has been principally associated with Rayleigh's dispersion theory and atmospheric geometry. A more detailed analysis of the radiative magnitude is required (and the inclusion of other phenomena, such as photon absorption).

The present study describes the theoretical framework used in the calculation of the algorithms. The data is sufficiently versatile allowing for comparative analysis experiments that vary the principal parameters and include factors such as an exponential atmosphere.

Key words: Monte Carlo method — computer simulation — atmosphere physics

---

1. INTRODUCCIÓN

Una característica interesante de las mediciones de irradiancia solar (en cielo claro) es su curva de ajuste (Fig. 1), cuya expresión compacta (no polinómica) [1]

 

 

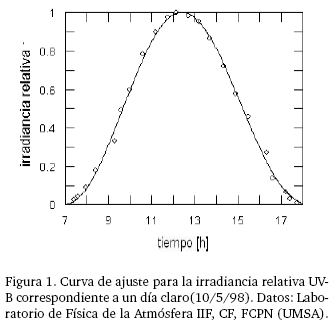
admite la forma (que facilita notablemente el ajuste recursivo por mínimos cuadrados)

Excepto el de α, los valores de los parámetros no varían significativamente en el ajuste para la irradiancia relativa (con la unidad como máximo).

Muy evidentemente, se trata de una gaussiana modificada con un polinomio de cuarto grado para forzar la anulación de sus extremos (el exponente cuadrático externo resulta esencial para mejorar la bondad de ajuste, especialmente en la proximidad de los mismos). No es importante si ésta es la única representación posible del perfil de los datos; la verdadera utilidad de la ec. (1) radica en que puede reemplazar a los datos experimentales cuando se trate de compararlos con datos simulados.

El propósito del presente trabajo es, justamente, el de producir puntos "experimentales" mediante el conteo de fotones incidentes en el lugar de observación, luego de pasar por un esquema dispersivo puramente elástico (Rayleigh) en la atmósfera terrestre convenientemente modelada.

Se pretende que el algoritmo general sea suficientemente flexible, de modo que permita el ensayo de diversas condiciones, dispersivas y geométricas, y la comparación directa de sus resultados con una curva del tipo (1) ajustada a mediciones efectivas.

2. GEOMETRÍA

Para todos los casos, la primera tarea es la ubicación de la fuente (el Sol) en un sistema de referencia adecuado y en tiempo local del observador.

En el sistema de coordenadas centrado en la Tierra pero fijo en el espacio {e'}, la dirección de los rayos solares sólo depende de la inclinación de la eclíptica

donde δ está calculada para cada día del año t_d mediante

siendo Ω = 2π/365,25). El sistema de coordenadas {e} centrado y fijo a la Tierra con el eje z orientado hacia el zenit del lugar de observación (latitud  y longitud λ) está relacionado con el anterior por la transformación e' = Re, en la cual R es la matriz

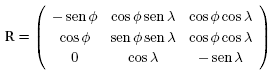
con Ø = ω(t − t₀ ) el ángulo horario (ω = π/12, velocidad angular de la rotación terrestre y to = 6). Entonces, la dirección de los rayos solares, desde el punto de vista del observador, está dada por el vector

cuyas componentes, teniendo en cuenta que  y en términos del tiempo solar t, son

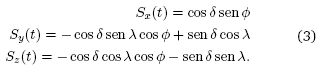
El tiempo solar aparente se calcula, en términos del tiempo de reloj t_r, usando las correcciones

donde t_L = Δφ/15 = 8,07/15 es la corrección por longitud y

es la ecuación del tiempo con Δt = t_d − 355 (t_d = 1 para el primero de enero).

Como se ve, el sistema de referencia y la dirección inicial instantánea de los fotones respecto de éste, quedan completamente determinados una vez que la posición del observador se especifica a través de su latitud y longitud (16.54S y 68.070 para este trabajo). Para cada fecha del año, el perfil de irradiancia relativa estará representado por el número de fotones incidentes en el lugar de observación en función del tiempo de reloj (en horas).

3. DISPERSIÓN

Sin embargo, una parte significativa de los fotones inciden después de ser desviados, una o varias veces, por las moléculas de aire. El recuento total, por tanto, debe ser el resultado de un esquema dispersivo que —en este caso— se supondrá completamente elástico.

El método Monte Carlo para la dispersión de Rayleigh comprende el sorteo de tres variables: el recorrido libre l y los ángulos azimutal Ø_f y zenital θ_f en el sistema local del fotón.

Cuando la dirección está determinada, el re­corrido resulta de la inversión de la distribución probabilística acumulativa para la densidad de Lambert-Beer, esto es:

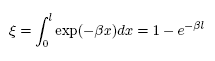
cuya inversa, teniendo en cuenta que ξ y 1− ξ tienen distribución uniforme en el intervalo [0,1] es

expresión que se usa para determinar el recorrido después de cada interacción fotón - molécula.

La distribución para el ángulo zenital (en el sis­tema local del fotón) es uniforme; por tanto, el sor­teo de esta variable procede según

Finalmente, la distribución probabilística para el ángulo zenital, derivada de la sección eficaz diferencial para la dispersión de Rayleigh, puede ser escrita, para los fines actuales, en la forma

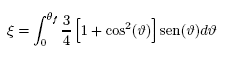
la cual, haciendo u = cosθ_f proporciona la ecuación cúbica

o bien, si x(ξ) = 4 − 8ξ,

Esta ecuación admite una solución real para u en función del número aleatorio ξ, inmediatamente utilizable para el sorteo del coseno del ángulo zenital, a saber:

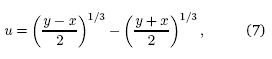
siendo

El sorteo de las tres variables es simultáneo pero, obviamente, el valor del número aleatorio es elegido independientemente para cada una de ellas.

4. MONTE CARLO INVERSO

Teniendo en cuenta la notoria simetría de la sección eficaz en la dispersión de Rayleigh, el proceso puede ser ejecutado partiendo del punto de observación en todas las direcciones previamente seleccionadas; tomando como exitosas aquellas para las cuales la trayectoria final del fotón apunta en dirección de la fuente.

Este mecanismo admite dispersión simple o múltiple, según el esquema algorítmico que sea planteado de inicio, junto con otras condiciones como la altura y densidad atmosféricas.

La rutina de cálculo empieza, por tanto, fijan­do la dirección inicial de los fotones mediante un ángulo zenital en el intervalo 0º ≤ θ_i ≤ 90º y uno azimutal 0º ≤ φ_i ≤ 359º en pasos Δθ_i y Δφ_i . El vector cartesiano del fotón es, entonces,

Un primer sorteo del recorrido según (5), por otra parte, permite determinar el radio

y la altura

donde R es el radio de la Tierra. Ahora, representando con H la altura máxima de la atmósfera y con  el diámetro aparente del disco solar (≈ 0,5º) cuando h > H se ensaya la dirección del fotón: si satisface

el número de fotones incidentes, N, incrementa en una unidad; contrariamente, el proceso termina y se procede nuevamente con (8).
Si h < H, el sorteo de las variables l, φ_f y u,, siguiendo lo descrito en la sección anterior, conduce a un nuevo cálculo del radio mediante

la altura h= r - R y el nuevo vector direccional del fotón (en términos de u y de  

Es fácil comprobar que los ensayos para h y para  proceden como antes. Cuando h < H, el sorteo de (l, φ_f, u) y los ensayos posteriores deben ser repetidos y corresponden a la dispersión múltiple del fotón.

 

 

                                  

También es posible la repetición completa del algoritmo descrito para n fotones en cada determinada dirección y cada intervalo Δt de tiempo (digamos, cada media hora desde la del levante hasta la del ocaso). Así, tomando Δθ_i = Δφ_i = 1º, el número total de fotones ensayados será 32760n para cada valor del tiempo de reloj t_r.

5. RESULTADOS

El sorteo de los números ξ para las variables (5), (6), y (7) se hizo usando una rutina adaptada del "Mersenne Twister" [2] para el ensamblador de 32 bites. Como toda simulación de tipo Monte Carlo, es natural que los resultados mejoran proporcional­mente a la cantidad de repeticiones del experimen­to (aleatorio). La serie de figuras 2a,...,2d ilustra claramente la evolución de los eventos favorables hacia una configuración muy semejante a la de la figura 1. Éstas corresponden al cómputo sobre el modelo más simple de una atmósfera esférica y ho­mogénea con altura h = 10 [km] y coeficiente de extinción β = 0,132 [km⁻¹], calculada de

 

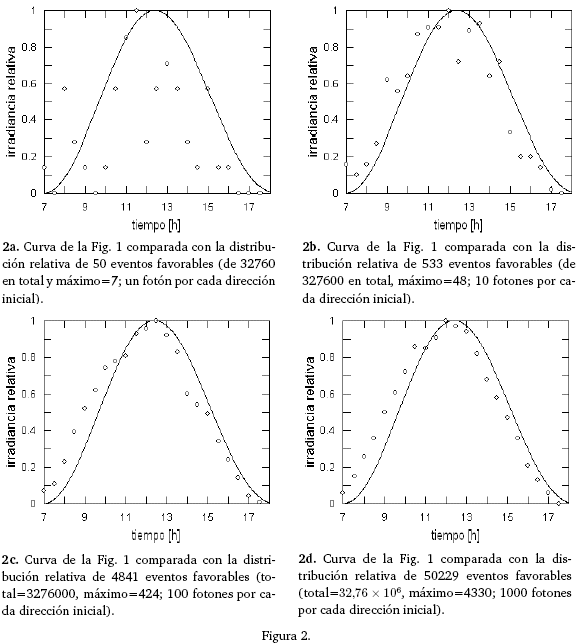
con n = 1 + 2,735 × 10⁻⁴, N = 2,687 × 1025 [m⁻³] (número de Loschmidt) y λ = 298 [nm].

En esta atmósfera, los fotones sufren dispersión múltiple desde la superficie atmosférica hasta el punto de observación (en realidad, por la simetría ya mencionada, se utiliza el método Monte Carlo inverso, descrito en la sección anterior: los fotones salen del punto de observación y se dispersan en la atmósfera hasta encontrar, eventualmente, la dirección de la fuente).

La figura 2d resume el resultado neto del procedimiento; excepto por el desplazamiento temporal, es aceptablemente comparable con la curva experimental para la misma fecha (10 de mayo, t_d = 130). De hecho, la curva corrida en media hora hacia la derecha que aparece en la figura 3, contrastada con la curva de ajuste de la Fig. 4 mediante la diferencia porcentual entre sus parámetros característicos (100(α_e −α_s)/α_e, etc.), rinde la tabla siguiente:

 

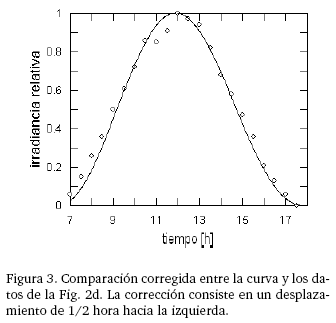
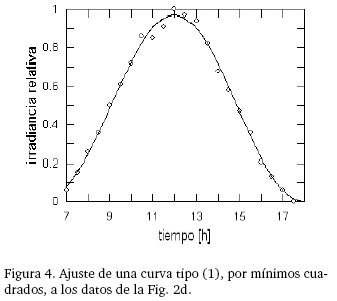
La curva experimental corregida y la curva de ajuste a los datos simulados concuerdan, pues, casi en un 85 %. Desafortunadamente, no ha sido posible encontrar una explicación convincente para el retraso de los puntos simulados en los gráficos 2; sin embargo, éste no afecta —según se ha visto— al perfil de la irradiancia relativa simulada.

Finalmente, tampoco el aumentar el tamaño de la atmósfera —en cuyo caso el factor de atenuación debe ser una función de la altura— parece contribuir con una mejora sustancial en el modelo. Así, tomando

 

α = 1/8,4 [km⁻¹] y β₀ = 0,132 [km⁻¹] (valores correspondientes al ajuste manual a los de la densidad para una atmósfera estándar [4]), el algoritmo se modifica de manera que el valor de β en (5) es recalculado para cada sorteo de la variable 1 siempre que h < H. El resto del procedimiento se mantiene como en el caso anterior.

El efecto numérico de tales modificaciones se muestra en las figuras 5a,... , 5d. Las apreciables fluctuaciones estadísticas y el crecimiento del número de fotones dispersados en comparación con el de los directos (reflejada en la altura de los puntos extremos en los gráficos), se explica fácilmente por la disminución —registrada— de eventos favorables cuando se incluyen sucesivamente la estratosfera y mesosfera a la troposfera, para la misma cantidad de fotones iniciales totales.

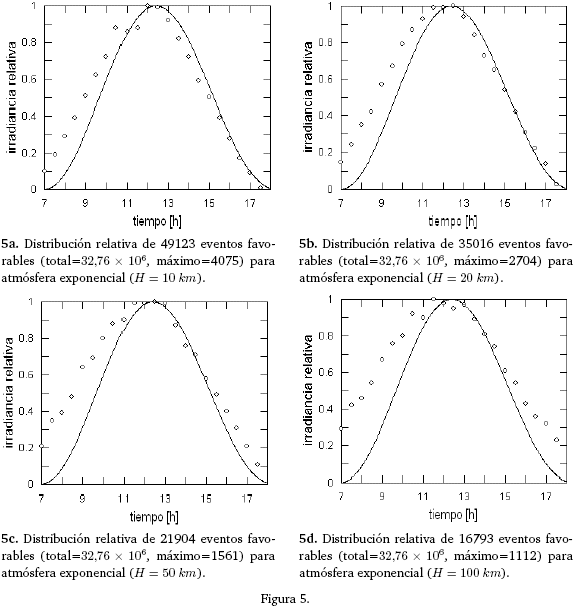
La manera de mejorar estos rendimientos es, pues, un fuerte incremento en el número de foto­nes iniciales y, seguramente, en un sorteo más sofisticado del salto dispersivo en términos de una integral de probabilidad acumulativa con coeficiente de extinción β(z) variable con la altura. Pero este esquema hace a los tiempos de cómputo innecesariamente prohibitivos, porque el propósito de este trabajo no es el de reproducir los resultados experimentales (Fig. 1.), sino sólo el de la forma de sus alturas relativas durante la trayectoria diurna de la fuente.

6. CONCLUSIONES

Dejando de lado cuestiones algo sofisticadas, como la real naturaleza del fenómeno dispersivo de fotones en la atmósfera terrestre o modelos muy detallados acerca de la composición de ésta, aún es pertinente la investigación acerca de las pro­piedades más inmediatas de ciertos modelos atmosféricos. Principalmente porque el formalismo matemático asociado a estos modelos es simple y permite el montaje de experimentos algorítmicos muy eficientes (factibles en equipos personales de computación).

Así, el propósito de reproducir numéricamente el perfil experimental de la irradiancia relativa, se logra mediante un algoritmo sencillo pero suficiente para simular las posibles trayectorias de los fotones en una atmósfera esférica y elástica. El hecho de que las distribuciones probabilísticas acumulativas para todas las variables sean invertibles ciertamente contribuye mucho a tal resultado.

Esto es, la esfericidad de la atmósfera terrestre y elasticidad (dispersión de Rayleigh) de las interac­ciones entre fotones y moléculas de aire son, pues, las dos propiedades suficientes para explicar la forma de la curva (1).

Hay dos implicaciones inmediatas: por tratarse de un proceso fundamentalmente estocástico, parece improbable que el perfil en cuestión pueda ser susceptible de una deducción teórica (la idea para este trabajo surgió de un intento es ese sentido); por otra parte, las técnicas asociadas a la transferencia radiativa harían poco adecuadas las refinaciones del algoritmo aquí empleado con el propósito de modelar, por ejemplo, las irradiancias absolutas [4].

REFERENCIAS

1.- Peñafiel V. M., Ajuste Analítico Sobre Mediciones UV-B en Cielo Claro, Rev. Bol. Fis. 7 I, 63 (2001).

2.- Matsumoto M. y Nishimura T., Mersenne TIvister: A 623-dimensionally equidistributed uniform pseudo­random number generator, ACM Transactions on Modeling and Computer Simulation, 8 3-30 (1998).         [ Links ]

3.- U. S. Committee on Extension to the Standard Atmosphere, U.S. Standard Atmosphere, 1976, NOAA, NASA, USAF, Washington D.C., (1976).        [ Links ]

4.- Emde C., Meyer J., Rozanov A., Rozanov V., and Bu­rrows J. P., Influences of horizontal atmospheric in­homogeneities on radiative transfer modelling, EGS 2001: 26-th General Assembly, 25-30 March, Nice, France (2001).        [ Links ]