ESTRUCTURA DEL ESPACIO DE PARÁMETROS PARA LAS ECUACIONES DEL CIRCUITO DE CHUA

G. M. Ramírez Ávila¹, J. A. C. Gallas²

¹Instituto de Investigaciones Físicas
Universidad Mayor de San Andrés
Casilla 8635 La Paz, Bolivia
²lnstituto de Física,
Universidade Federal do Rio Grande do Sul,
91501-970 Porto Alegre, Brasil

---

RESUMEN

Se estudia en forma detallada el espacio de parámetros para las ecuaciones correspondientes al circuito de Chua con dos y tres parámetros que en primera instancia confirman los resultados obtenidos en [1] y además muestra la exis­tencia de estructuras denominadas "camarones" que denotan periodicidades y un hub organizador de estas estructuras que dan lugar a "espirales".

Descriptores: caos — circuito de Chua — periodicidades — sistemas dinámicos dinámica no lineal.

---

ABSTRACT

We study in detail the parameter space for nonlinear differential equations corresponding to the Chua's circuit. Our analysis of two and three parameters confirms preliminary results obtained in [1]. In addition, it shows the existence of structures denoting periodicities called "shrimps" and a hub which organizes these structures into "spirals".

Key words: chaos — Chua's circuit — periodicities — dynamical systems — nonlinear dynamics.

---

1. INTRODUCCIÓN

Si bien el estudio del caos experimenta una reconfiguración local [2] uno de cuyos principales exponentes fue E. N. Lorenz³ con su modelo que trata­ba de explicar la dinámica atmosférica del planeta [3] y que dio lugar al primer atractor caótico ob­servado en un sistema autónomo de tercer orden [4]. Con el transcurso de los años, fueron descritos muchos sistemas de diferentes tipos que exhibían caos, pudiéndose encontrar una descripción de mu­chos de ellos en [5]. Uno de los tipos de sistemas más atractivos son los circuitos eléctricos, los cuales no sólo permitieron su utilización como artefactos de demostración del caos sino también como verdaderos objetos de estudio científico [6]. Entre es­tos circuitos eléctricos que pueden presentar comportamiento caótico, se pueden citar los propuestos por Testa et. al. [7], Sprott [8] y el paradigmático circuito de Chua [9] que será el objeto de estudio del presente trabajo. El artículo está organizado de la siguiente manera: En la Sección 2 se presenta sucíntamente el circuito de Chua y las ecuaciones que lo modelan. En la Sección 3 se muestran los resultados del análisis del espacio de parámetros para las ecuaciones del circuito de Chua con dos y tres parámetros. Finalmente, en la Sección 4 se dan las conclusiones y perspectivas de la investigación realizada.

2. CIRCUITO DE CHUA

El circuito de Chua es uno de los modelos más populares que exhiben caos puesto que es el circuito autónomo más simple capaz de mostrar este comportamiento puesto que tiene orden 3 debido a que contiene 4 elementos no lineales: el diodo de Chua que básicamente es una resistencia no lineal y dos condensadores, una bobina y una resistencia.         

Se lo introdujo a partir del análisis de un sistema electrónico ampliamente tratado por varios autores [9-11] y que fue descrito con cierto detalle en [1](ver Figura 1, la cual fue tomada de [1]). 

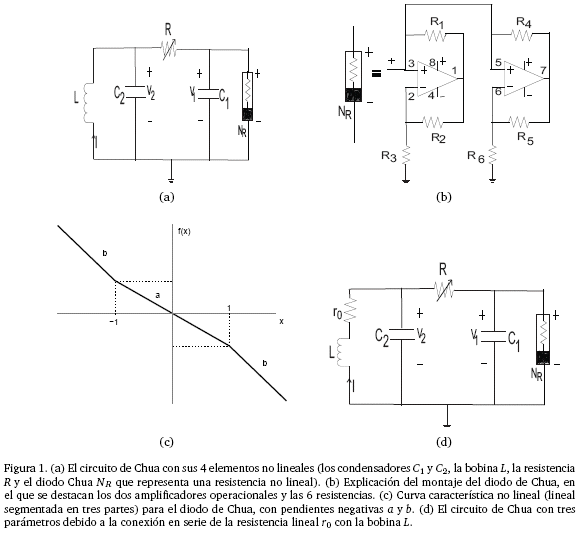
Por la riqueza⁴ en cuanto a su comportamiento , el circuito Chua ha sido y es objeto de mucha investigación científica, convirtiéndose en un paradigma  universal para el caos cuyas ecuaciones se pueden escribir:

siendo que se puede expresar por

 

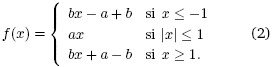
Los parámetros de control α, β, γ, están relacionados con los componentes del circuito mostrado en la Figura 1(d) en la forma:

En tanto que a y b representan las pendientes negativas de la curva característica de la Figura 1(c). Se debe hacer notar que en el caso en el que no se considera la resistencia r₀, el parámetro γ es nulo y el sistema puede describirse en términos de sólo dos parámetros. Para el estudio que realizamos, se consideraron para el modelo con dos parámetros los valores a = -0.724 y b = -1.22, además de las condiciones iniciales: x₀=0.10, y₀ =0.15 y z₀= 0.01; mientras que para el modelo con tres parámetros se consideraron los valores a = -8/7, b=-5/7, las condiciones iniciales: x₀ = 1.10, y₀ = 0.12 y z₀ = 0.01 en todos los casos γ=0.30 (plano β vs. α), α=17.00 (plano γ vs. β) y β=30.00 (plano γ vs. α). 

 

3. ANÁLISIS DEL ESPACIO DE PARÁMETROS

El análisis detallado del espacio de parámetros de sistemas discretos se ha hecho común a partir de los trabajos realizados en el mapa de Hénon [12] y que en el último tiempo fue de interés del famoso E. N. Lorenz [13] así como en mapas cuadráticos y cúbicos [14]. Recientemente, análisis de sistemascontinuos fueron publicados encontrándose aspectos muy interesantes en la dinámica de los sistemas considerados [15-18]. Para nuestro análisis, se utilizan los valores de los parámetros mencionados en la Sección 2 y respecto a las características del método de integración, se debe señalar que se utilizó el esquema de Runge-Kutta de cuarto orden con un paso de tiempo fijado en h=10-³, un transiente de 7x 10⁴ y un tiempo total de integración de 1.4 x 106.

3.1. Modelo de Chua con dos parámetros

Para empezar nuestro análisis, primero se incluye la figura que se mostró en [1] y que representaba un intento de definir regiones en las cuales el sistema presentaba comportamiento periódico, caótico o divergente; para ello se calculó el máximo exponente de Lyapunov haciendo variar el parámetro a desde 2.0 hasta 102.0 con un espaciado de 0.5, en tanto que β se varió tratando de determinar las fronteras que separan los regímenes periódicos de los caóticos y los divergentes y se tuvieron valores comprendidos entre 2.0 hasta 1539.9 tal como se muestra en la Figura 2(a). Integrando las ecua­ciones para el valor del parámetro γ=0 y bajo las características numéricas señaladas anteriormente, se obtienen paneles en forma de mapa de bits, en los cuales, el color proporciona el máximo exponen­te de Lyapunov con resoluciones de 50 x 50 pixe­les (Figura 2(b)) y 200 x 200 pixeles (Figura 2(c)). Como se puede observar en la Figura 2(b), las regiones determinadas en la Figura 2(a) parecen re­producirse considerando que para valores negativos del exponente máximo de Lyapunov se tiene un comportamiento periódico para el sistema y para valores positivos se tiene comportamiento caótico y para los valores positivos mayores, se podría hablar de comportamientos divergentes; sin embargo, si se examina con un poco más de detalle este panel, podemos ver que hay una zona "patológica" tanto para valores pequeños de α como de β. Si se aumenta la resolución como se muestra en la Figura 2(c), las regiones periódicas, caóticas y divergentes siguen presentándose pero además, aparece una región para valores pequeños de β y un rango de valores de α comprendido entre 0 y 20 aproximadamente, en la cual hay una diferencia notoria respecto al entorno.

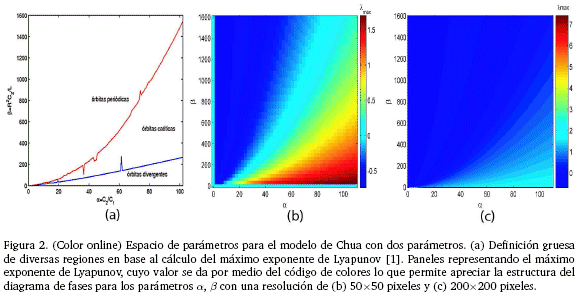
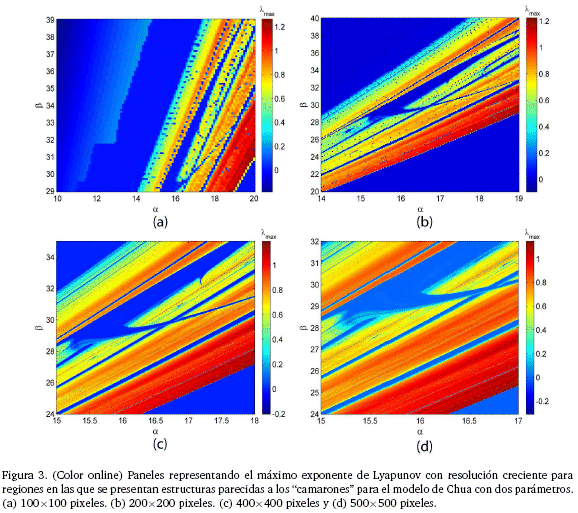
Por lo mencionado en el anterior párrafo, parece más probable encontrar comportamientos interesantes justamente en esas regiones "patológicas", por lo que realizamos integraciones de manera de tener resoluciones crecientes en estas regiones y así poder ver si estructuras tipo "camarón" aparecen en el diagrama de fases. Los resultados, se muestran en la Figura 3, en la cual se trabajó con resoluciones crecientes. Así, en la Figura 3(a), la resolución es de 100 x 100 pixeles y se ve que aparece una zona periódica (exponente máximo de Lyapunov negativo) que parece tener la forma de "camarón"; en la Figura 3(b), se focaliza más a la región con el comportamiento periódico y se aumenta la resolución a 200 x 200 pixeles, con lo que se nota mejor la región periódica que a pesar de tener la apariencia de un "camarón", no parece haber que este tipo de estructuras sea densa en el espacio de parámetros, lo que se comprueba focalizando esta región periódica y aumentando la resolución a 400 x 400 pixeles (Figura 3(c)) y a 500 x 500 pixe­les (Figura 3(d)). Este último aspecto, hace que estudiar este sistema no sea muy atractivo desde el punto de vista de encontrar auto-similaridades ya sean periódicas como caóticas tal como se estudia en [15-18].

3.2. Modelo de Chua con tres parámetros

Procediendo de la misma manera que en la sub-sección 3.1, primeramente se puede hacer un estudio grueso del espacio de parámetros para luego ir afinando la escala y aumentando la resolución en las posibles regiones de interés; es decir, en las zonas en las que aparecen las estructuras de "camarones" que denotan periodicidad. En la Figura 4(a), con una resolución de 100 x 100 pixeles, se puede ver de manera gruesa las regiones en las cuales se tiene comportamiento periódico y caótico, dependiendo del valor del exponente máximo de Lyapunov y se puede notar que para valores pequeños de los parámetros α y β parece presentarse un comportamiento distinto al del entorno por lo que podría ser una región de interés, situación que se confirma al aumentar la resolución a 200 x 200 pixeles (Figura 4(b)) y con la misma resolución pero concentrados en una región menor (Figura 4(c)), en la que la región de interés aparece claramente y está marca­da con un círculo en la Figura 4(c).

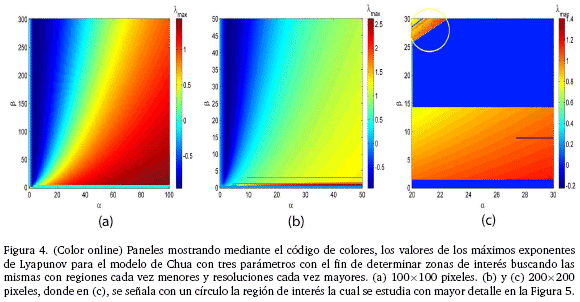
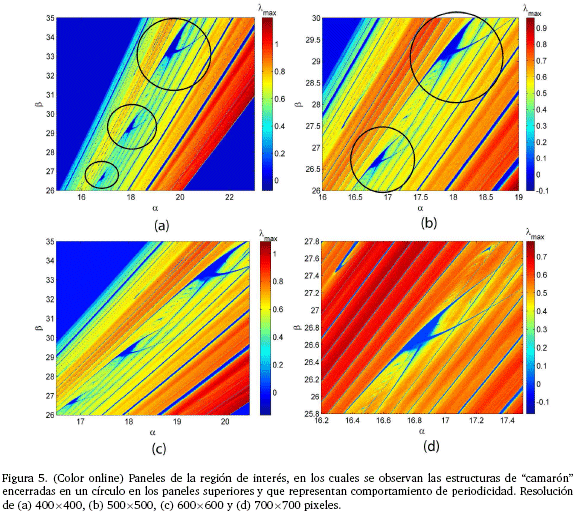
Ahora, si se estudia la región de interés, se puede notar que con una resolución de 400 x 400 pixe­les (Figura 5(a)), aparecen ya claramente tres es­tructuras de "camarón" que representan regiones de periodicidad del sistema con valores para el ex­ponente máximo de Lyapunov menores o iguales a cero (λ _max ≤ 0)) y focalizándose en los dos "camarones mayores" de la Figura 5(a) y aumentando la resolución a 500 x 500 pixeles (Figura 5 (b)) se ve con mayor claridad los "camarones" y su entorno, lo que permitiría estudiar de manera más profunda las auto-similaridades y los aspectos que estas implican tales como diagramas de bifurcación y rutas al caos que aparecen en el modelo de Chua con tres parámetros. De la misma manera, se mejora aun más la resolución en la Figura 5(c) a 600 x 600 pixe­les y se aprecian con mayor detalle los "camarones" y contiguos a éstos, se ven aparecer tenuemente otras estructuras que denotan periodicidad; por lo anterior, se hace un acercamiento a uno de los "camarones" con una resolución de 700 x 700 pixeles (Figura 5(d)) , donde se observa con más claridad las estructuras de periodicidad en las proximidades (entre las antenas) del "camarón".

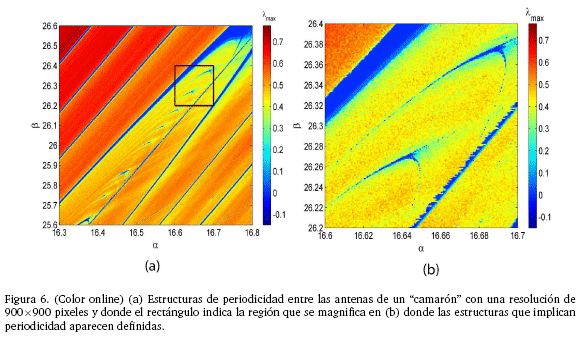
Las estructuras anteriores se ven con mayor detalle (resolución de 900 x 900 pixeles) en la Figura 6, donde en la Figura 6(a) se muestran las estructuras que denotan periodicidades y que parecen estar organizadas in­dependientemente a cómo lo están los "camarones" de la Figura 5; este hecho es por demás interesante puesto que implicaría que las estructuras de la Figura 6 y las estructuras de "camarones" de la Figura 5 están superpuestas. En tanto que en la Figura 6(b) se muestra un acercamiento correspondiente al rectángulo de la Figura 6(a) y en donde las es­tructuras de periodicidad aparecen más claramente definidas.

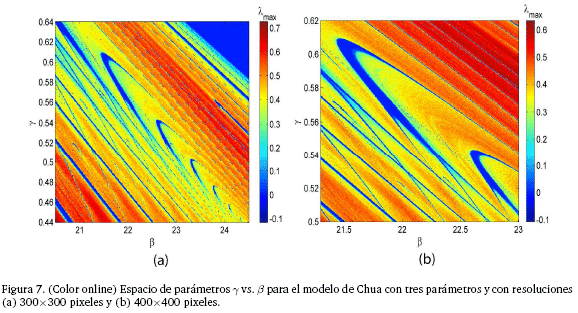
Si bien hasta ahora se trabajó con el mismo es­pacio de parámetros que el utilizado con el mode­lo de dos parámetros, es posible también trabajar con el espacio de parámetros en términos de los parámetros (β, γ) y con el correspondiente (α, γ). La construcción del espacio de parámetros en el plano (β, γ) permite apreciar ya a bajas resoluciones una gran cantidad de estructuras que denotan periodicidad (Figura 7) y que por su forma se ase­mejan a las mostradas en la Figura 6. En la Figura 7(a) que tiene una resolución de 300 x300 pixeles,se muestra una sucesión de estas estructuras, similar a la sucesión que se observa en la Figura 6(a), lo que sugiere la existencia de un hub⁵ de periodicidad tal como el que se reporta para el circuito de Nishio [18]. En la Figura 7(b) se muestra un panel con una resolución de 400 x 400 pixeles, donde se observa con mayor detalle la estructura individual de estas regiones en el espacio de parámetros que denotan periodicidad.

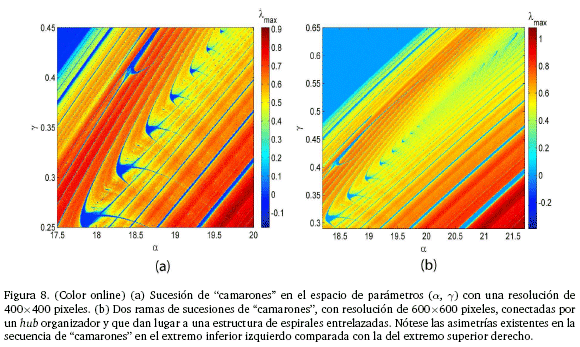
Finalmente, trabajando con el espacio de parámetros (α, γ), se obtienen los resultados más vistosos y que muestran una sucesión nítida de "camarones" incluso para resoluciones no muy altas (400 x 400 pixeles), como la mostrada en la Figura 8(a), la cual sugiere la existencia de un hub organizador de espirales entrelazadas como en [18] y que se muestra en la Figura 8(b), la cual tiene una resolución de 600 x 600 pixeles. Es interesante observar con mayor detalle la Figura 8(b) puesto que si bien en ella aparece el hub organizador, éste no presen­ta la simetría que se reporta en [18]; en nuestro caso, hay una asimetría en las convergencias entre la rama superior e inferior.

4. CONCLUSIONES Y PERSPECTIVAS

Como resultados más importantes del presente artículo, se puede señalar que se verificaron los re­sultados obtenidos en [1] en lo que se refiere a la determinación de las regiones en las cuales el comportamiento del sistema es periódico o caótico para el modelo con dos parámetros. Por otra parte, para este mismo modelo, se pudieron obtener estructuras que se asemejan a los "camarones" reportados en [12, 14-17] pero estas estructuras parecen de­formadas y su densidad en el espacio de paráme­tros no parece ser muy alta lo que significaría que no es un modelo muy atractivo para un estudio más profundo. Para el modelo con tres parámetros, se obtienen claramente las estructuras de "camarón", aspecto que pone en evidencia la importancia del parámetro y en la aparición de estas estructuras, lo que hace posible que se pueda encarar un análisis más detallado de este modelo para estudiar las auto-similaridades y aspectos tales como los diagra­mas de bifurcación y rutas al caos; se nota también que la densidad de estas estructuras es ya considerable para emprender los estudios citados anteriormente y resultados preliminares muestran que también es posible encontrar estructuras de tipo espiral similares a las halladas en [18] . Vale la pena resaltar el hecho de que para el modelo de Chua con tres parámetros, en el espacio de fases (α y β) los "camarones" aparecen claramente pero en principio, no con una densidad considerable; sin embargo, en las regiones contiguas, entre las "antenas" de los mismos, se encuentran sucesiones de estructuras que denotan periodicidad y al parecer existen dos tipos de estructuras denotando periodicidades que son independientes entre sí. En tanto, en el espacio (β, γ), aparecen sucesiones de estructuras de periodicidad similares a las encontradas en las regiones aledañas a los "camarones" del espacio (α y β), lo que sugiere que puede existir un hub organizador de las mismas y también espirales entrelazadas. Por otra parte, en el espacio (α, γ), se encontraron sucesiones de estructuras de periodicidad y también se observó el hub organizador similar al encontrado en [18] cuando se trata el circuito de Nishio [20]; sin embargo, en nuestro caso, las convergencias de las estructuras que denotan periodicidad son asimétricas, aspecto interesante que todavía no lo entendemos a cabalidad. Este último aspecto debe ser estudiado con mayor detalle, ajustando los valores de los parámetros de manera de tener una espiral completa en un solo plano. La comparación de las características físicas del modelo de Chua con el modelo de Nishio muestran que en el primero las ecuacio­nes conllevan una mayor complejidad por lo que se espera que la riqueza en cuanto a la presencia de "camarones", hubs y espirales sea también mayor, lo que constituye un desafío para futuras investigaciones. Otras versiones del circuito de Chua, como las estudiadas en [21, 22], donde la no linealidad es cúbica puede ser tratada de la forma en la que se hizo en este trabajo. El conocimiento en profun­didad de sistemas tan conocidos y populares como el circuito de Chua, alienta el potencial trabajo que puede realizarse al respecto para la verificación experimental de la existencia de estas estructuras, cuyo tratamiento teórico es también importante para la comprensión de la génesis de los hubs y espirales en los diagramas de fase [23].

5. AGRADECIMIENTOS

GMRA agradece a la Third World Academy of Sciences (TWAS) y a la Academia Nacional de Ciencias de Bolivia (ANCB) por el premio otorgado. JACG agradece al Conselho Nacional de Desenvol­vimento Científico e Tecnológico (CNPq) por el fi­nanciamiento para la investigación y también agra­dece a la Air Force Office of Scientific Research (AFOSR) por el apoyo bajo contrato FA9550-07-1- 0102.

REFERENCIAS

1.- G. Conde Saavedra & G. M. Ramirez Avila, "Estudio de dos circuitos caóticos", Revista Boliviana de Fisica, vol. 13,pp. 58-74, 2007.        [ Links ]

2.- D. Aubin & A. Dahan Dalmedico, "Writing the history of dynamical systems and chaos: longue durée and revolution, disciplines and cultures", Historia Mathe­matica, vol. 29, pp. 273-339, 2002.        [ Links ]

3.- E. N. Lorenz, "Deterministic nonperiodic flow", Jour­nal of the Atmospherics Sciences, vol. 20, pp. 130-141, 1963.        [ Links ]

4.- E. Rietman, Creating artificial life: self-organization. New York: Windcrest/McGraw-Hill, 1993.        [ Links ]

5.- T. Tel & M. Gruiz, Chaotic Dynamics. An Introduction Based on Classical Mechanics. Cambridge: Cambridge University Press, 2006.        [ Links ]

6.- J. C. Sprott, Chaos and time-series analysis: Oxford University Press, 2003.        [ Links ]

7.- J. Testa, J. Pérez, & C. Jeffries, "Evidence for Universal Chaotic Behavior of a driven Nonlinear Oscillator", Physical Review Letters, vol. 48, pp. 714-717, 1982.        [ Links ]

8.- J. C. Sprott, "A new class of chaotic circuit", Physics Letters A, vol. 266, pp. 19-23, 2000.        [ Links ]

9.- T. Matsumoto, S. Tanaka, & L. O. Chua, "Simplest chaotic nonautonomous circuit", Physical Review A, vol. 30, pp. 1155-1157, 1984.        [ Links ]

10.- L. O. Chua, Y. Yao, & Q. Yang, "Devil's staircase rou­te to chaos in a nonlinear circuit", International Jour­nal of Circuit Theory and Applications, vol. 14, pp. 315-329, 1986.        [ Links ]

11.- T. Matsumoto, L. O. Chua, & R. Tokunaga, "Chaos via torus breakdown (nonlinear circuit)", IEEE Tran­sactions on Circuits and Systems, vol. CAS-34, pp. 240-253, 1987.        [ Links ]

12.- J. A. C. Gallas, "Structure of the parameter space of the Hénon map", Physical Review Letters, vol. 70, pp. 2714, 1993.        [ Links ]

13.- E. N. Lorenz, "Compound windows of the Hénon­map", Physica D: Nonlinear Phenomena, vol. 237, pp. 1689-1704, 2008.        [ Links ]

14.- J. A. C. Gallas, "Dissecting shrimps: results for some one-dimensional physical models", Physica A: Statis­tical Mechanics and its Applications, vol. 202, pp. 196- 223, 1994.        [ Links ]

15.- C. Bonatto, J. C. Garreau, & J. A. C. Gallas, "Self­similarities in the frequency-amplitude space of a loss-modulated CO2 laser", Physical Review Letters, vol. 95, pp. 143905, 2005.        [ Links ]

16.- C. Bonatto & J. A. C. Gallas, "Accumulation hori­zons and period adding in optically injected semicon­ductor lasers", Physical Review E (Statistical, Nonli­near, and Soft Matter Physics), vol. 75, pp. 055204-4, 2007.        [ Links ]

17.- C. Bonatto, J. A. C. Gallas, & Y. Ueda, "Chao-tic phase similarities and recurrences in a damped­driven Duffing oscillator", Physical Review E (Statisti­cal, Nonlinear, and Soft Matter Physics), vol. 77, pp. 026217-5, 2008.        [ Links ]

18.- C. Bonatto & J. A. C. Gallas, "Periodicity Hub and Nested Spirals in the Phase Diagram of a Simple Re­sistive Circuit", Physical Review Letters, vol. 101, pp. 054101-4, 2008.        [ Links ]

19.- A. L. Barabási, Linked. The new science of ne­tworks . Cambridge, Massachusetts: Perseus Publis­hing, 2002.        [ Links ]

20.- Y. Nishio, N. Inaba, S. Mori, & T. Saito, "Rigorous analyses of windows in a symmetric circuit", IEEE Transactions on Circuits and Systems, vol. 37, pp. 473­487, 1990.        [ Links ]

21.- G.-Q. Zhong, "Implementation of Chua's circuit with a cubic nonlinearity", IEEE Transactions on Cir­cuits and Systems I: Fundamental Theory and Applica­tions, vol. 41, pp. 934-941, 1994.        [ Links ]

22.- A. Tsuneda, "A gallery of attractors from smooth Chua's equation", International Journal of Bifurcation and Chaos, vol. 15, pp. 1-49, 2005.        [ Links ]

23.- J. A. C. Gallas, "Phase diagrams for a system stu­died by Glendinning", Instituto de Física Universida­de Federal do Rio Grande do Sul, 2008, pp. 1-4.(no publicado).        [ Links ]

NOTAS

¹ Email: mravila@fiumsa.edu.bo
Website: http://www.fiumsa.edu.bo/docentes/mramirez/

² gEmail: jgallas@if.ufrgs.br
Website: http://www.if.ufrgs.br/∼jgallas/

³Fallecido recientemente el 16 de abril de 2008.

⁴ Una galería de atractores obtenidos con un osciloscopio puede encontrarse en [1] G. Conde Saavedra & G. M. Ramirez Avila, “Estudio de dos circuitos caóticos”, Revista Boliviana de Fisica, vol. 13, pp. 58-74, 2007.

⁵ Se usa el término en inglés por comodidad y por la popularidad que adquirió por su utilización en aspectos relacionados a redes complejas (ver por ejemplo [19] A. L. Barabási, Linked. The new science of networks. Cambridge, Massachusetts: Per­seus Publishing, 2002.) y a redes de computadoras en particu­lar. El significado de hub es el de centro ya sea concentrador o distribuidor, donde convergen muchas conexiones por lo que la red depende fuertemente de este punto central.