ARTÍCULO ORIGINAL

UNA DESCRIPCIÓN DEL MÉTODO DE ONDAS PLANAS PARA
EL CÁLCULO DE BANDAS FOTÓNICAS

R. Archuleta-García', M. B. Manzanares-Martínez², J. Manzanares-Martínez3

'Programa de Posgrado en Ciencias (Física) de la Universidad de Sonora
éxico
² Unidad Regional Sur de la Universidad de Sonora
Boulevard Lázaro Cárdenas No. 100, Navojoa, Sonora 85880, México
³Centro de Investigación en Física de la Universidad de Sonora
Apartado Postal 5-088, Hermosillo, Sonora 83190, México

---

RESUMEN

Se presenta una descripción detallada del Método de Ondas Planas para el cálculo de estructuras de banda fotónicas. El sistema a estudiar es un medio infinito en donde la función dieléctrica y el campo electromagnético son periódicos en una dimensión. Por medio de series de Fourier, hacemos expansiones de la función dieléctrica y del campo electromagnético. Estas expansiones sirven para plantear a la ecuación de onda como una ecuación de valores propios. Mostramos explícitamente los elementos de matriz de la ecuación de eigenvalores y proponemos un sencillo programa en Matlab que calcula bandas fotónicas.

Descriptores: Banda Fotónica, Cristal Fotónico.

---

 

 

1. INTRODUCCIÓN

Es conocido que en sólidos cristalinos la periodicidad atómica impide la propagación de los electrones que tie­nen una energía situada en la llamada brecha de energías prohibidas. La existencia de zonas de conducción prohi­bidas o permitidas determina las propiedades de los lla­mados semiconductores. Para el entendimiento de las ca­racterísticas físicas de estos cristales atómicos se han de­sarrollado diversos métodos de cálculo.

En 1987 E. Yablonovitch [1] propuso inhibir la pro­pagación de luz mediante la fabricación de materiales dieléctricos. La idea es construir de forma artificial es­tructuras que tengan una periodicidad similar a los cris­tales atómicos, pero en una escala diferente. La nueva estructura cristalina es unas 1000 veces más grande que un cristal atómico. Esta estructura difracta a los foto­nes (luz) de la misma forma que los cristales atómicos difractan electrones. Por esta razón, se les ha llamado Cristales Fotónicos (CF) y asimismo nació el concep­to de Brecha de Energía Prohibida (BEP) para fotones. Los CF abren vías de investigación muy prometedoras para la manipulación de fotones en la industria de las telecomunicaciones. En particular es de gran relevancia la integración de dispositivos fotónicos y electrónicos.

El estudio de las propiedades tecnológicamente más importantes para CF probablemente estará ligado al estudio de heteroestructuras, es decir, la superimposi­ción de dos diferentes redes cristalinas que den lugar a fenómenos de interés tecnológico. La idea de juntar dos diferentes redes cristalinas ha probado ser una via exitosa en cristales at´omicos, en donde la conjunci´on de diferen tes redes cristalinas dió lugar al invento del transistor, génesis de la revolución electrónica.

En la perspectiva de nuestro interés en las heteroes­tructuras de cristal fotónico hemos desarrollado un estu­dio sistemático del método de ondas planas (MOP) [2]. A pesar de la popularidad del MOP para CF, cuando el investigador o estudiante desea implementar este méto­do de cálculo tiene que recurrir a los artículos originales [3-7] en donde no se ilustran en detalle diversos aspec­tos matemáticos importantes. Este trabajo nace con la idea de servir de guía, paso a paso, para el estudiante interesado en iniciarse en el cálculo con el MOP.

Después de que en 1987 los cristales fotónicos fue­ron propuestos, comenzaron los primeros estudios ex­perimentales sobre cristales fotonicos [3]. Los primeros cálculos de bandas fotonica.s fueron realizados por los especialistas en bandas de energía electrónica los cuales utilizaron por primera vez el método de ondas planas [4- 6]. Sin embargo, estos primeros resultados no estaban en concordancia con los resultados experimentales, ya que los cálculos predecían BEP en lugares en donde el ex­perimento no las detectaba [3]. El problema venía de la utilización de una teoría de campo escalar. Los calcu­los imitaban el caso de BEP electronicas, en donde se busca los eigenvalores de la ecuación de onda de Sch­rodinger [4-6]. Pero utilizar una teoria escalar no es el procedimiento correcto. Para BEP fotónicas es necesario resolver las ecuaciones de Maxwell. El cálculo de bandas fotonicas necesita ser planteado como la solución vecto­rial del campo electromagnético para obtener resultados correctos [7-9].

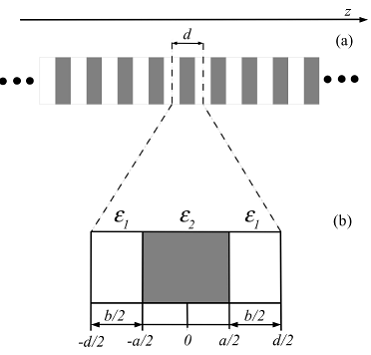
-d/2 -a/2      O    a/2    d/2

Figura 1. (a) Cristal fotónico con periodicidad unidimensio­nal; d corresponde al ancho de la celda unitaria. (b) Celda uni­taria conformada por dos materiales de constantes dieléctricas el y C2.

En este trabajo vamos a detallar el MOP analizan­do el caso mas sencillo que es un cristal unidimensional (1D). En este sistema la transformada de Fourier se cal­cula analíticamente. Se muestra en forma explícita los elementos de matriz de la ecuación de eigenvalores. Fi­nalmente proponemos un sencillo programa en Matlab, el cual permite calcular una banda fotónica 1D.

2. LA SERIE DE FOURIER PARA LA FUNCION DIELECTRICA

Comenzamos nuestro análisis planteando la ecuación de onda 1D

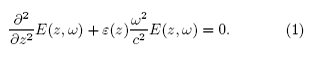
En esta ecuación consideramos que la función dieléctrica forma una red periodica infinita como ilustra la Fig. la. Toda red esta conformada por una red y una base. En la Fig. lb se muestra la base o celda unitaria que esta con­formada por los materiales e_l y e₂ cuyos espesores son a y b, respectivamente. La longitud de la celda unitaria es d=a+b.

La forma de la función dieléctrica puede expresarse matemáticamente en el intervalo -d/2 < z < c/12 como en [101

donde la funcion de Heaviside es

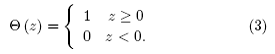
Ya que toda función periódica puede expresarse en ter­minos de una serie de Fourier, expresamos la función dieléctrica en la celda unitaria de la forma

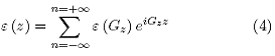
donde G„ es un vector de la red reciproca y toma va­lores  . Para conocer los coeficientes de la serie de Fourier  multiplicamos por e integramos ambos lados de la ecuación,

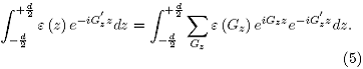
La integral del lado derecho se desarrolla en el Apéndice

1. El resultado es

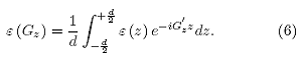
Para calcular estos coeficientes primero planteamos el caso en que G, = O . Sustituimos (2) en (6) para obtener

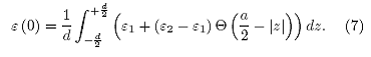
Separamos los intervalos en donde la función dieléctrica permanece constante,

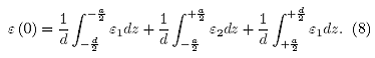
El coeficiente de Fourier es entonces

donde la fracción de llenado f se define como f = a/ d.

Ahora consideraremos el caso cuando . Los
coeficientes de Fourier se obtienen sustituyendo (2) en (6) para obtener

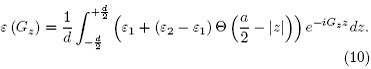
 Separarnos de nuevo la integral en los intervalos en los cuales la función dieléctrica se conserva constante para obtener

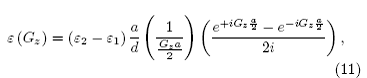
la que se puede reducir a

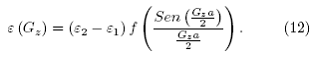
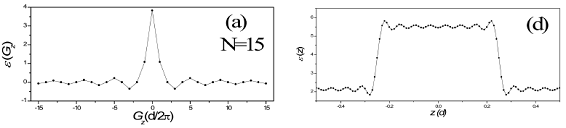
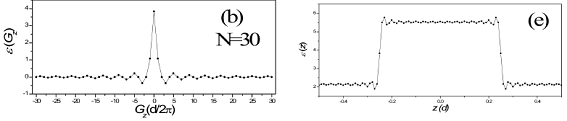
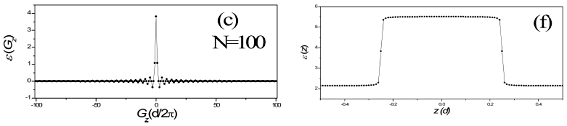
Figura 2. Los páneles (a), (b) y (c) muestran los valores de los coeficientes de Fourier calculados para N=15, 30 y 100. Los páneles (d), (e) y (f) muestra la función dieléctrica en el espacio real para N=15, 30 y 100.

Como un ejemplo de la representación de la función dielectrica en términos de la serie de Fourier considera­mos una celda unitaria de espesor d = 10^-8m y f=0.5. Las funciones dieléctricas son є1 = 5,52 y є₂ = 2,13 [10]. Presentamos en las Fig. 2 los coeficientes de Fou­rier [páneles (a)-(c)] y la serie de Fourier de la función diléctrica [páneles (d)-(f)] para los casos N=15, 30 y 100. Se observa que a medida que el numero de ondas planas aumenta, los coeficientes de Fourier tienden al valor ce­ro. Por su parte, la función dieléctrica converge mejor a medida que se ocupan más valores de N, es decir, más ondas planas. En el Apéndice 2 incluimos un programa en Matlab que realiza estas figuras para diferentes valores de N

3. ECUACIÓN DE VALORES PROPIOS

Para resolver la ecuación de ondas en términos de la serie de Fourier es más conveniente expresar la esta ecuación como

donde es posible obtener una serie de Fourier del inverso de la función dieléctrica de la forma

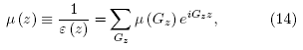
cuyos coeficientes de Fourier son

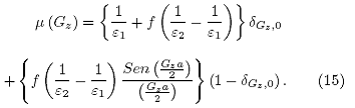
El campo el´ectrico tambien puede expresarse en términos de serie de Fourier en la forma

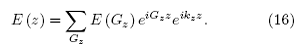
Sustituyendo las expresiones en serie de μ(z) y E(z) en (13) que define la ecuaci´on de onda tenemos

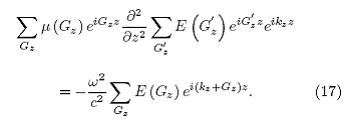
Realizando las derivadas en el primer término tenemos:

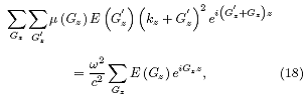
donde hemos eliminado en ambos lados la exponencial  . Multiplicando (18) por   e integrando sobre la celda unitaria, se obtiene

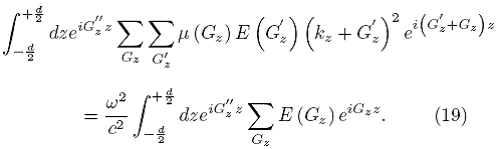
Como se muestra en el Apéndice 1, identificamos las fun­ciones delta:

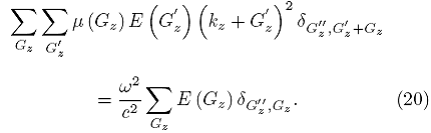
Aplicando (20) a (19) se obtiene

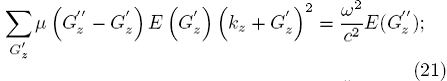
finalmente, si cambiamos el índice mudo   por Gz tenemos

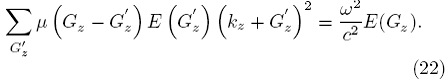
4. REPRESENTACIÓN MATRICIAL DE LA ECUACIÓN DE VALORES PROPIOS

La estrategia para resolver la ecuación de eigenvalo­res es plantear una ecuación matricial. Para obtenerla desarrollamos el lado izquierdo de (22),

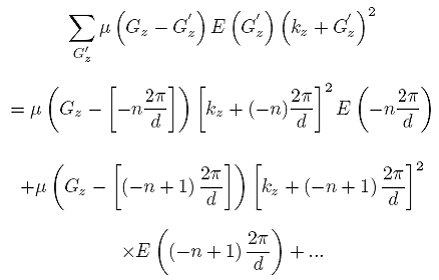
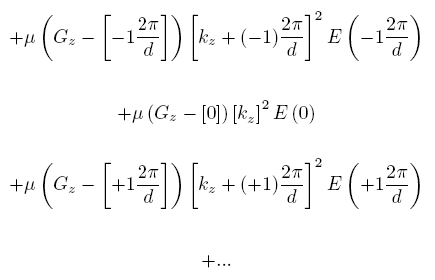
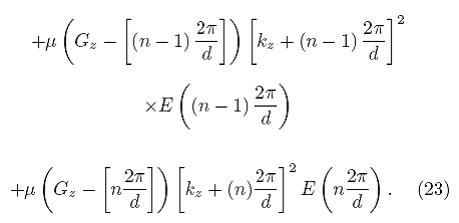
Esta larga suma puede escribirse como una multiplicación de un vector rengl´on por un vector columna,

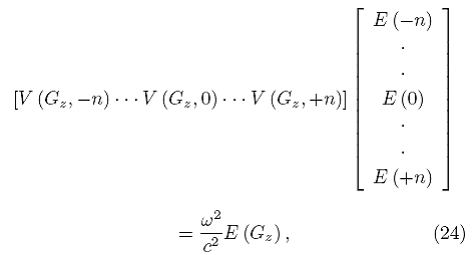
donde cada elemento del renglón es

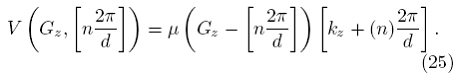
La ec. (25) es válida para cualquier valor de G. Para lograr un sistema cuadrado es necesario plantear esta ecuación para los valores entre -N y N, incluyendo N = 0. Procediendo de esta forma obtenemos

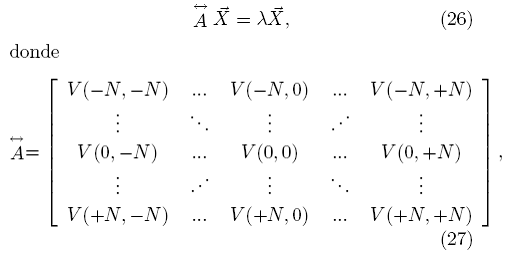
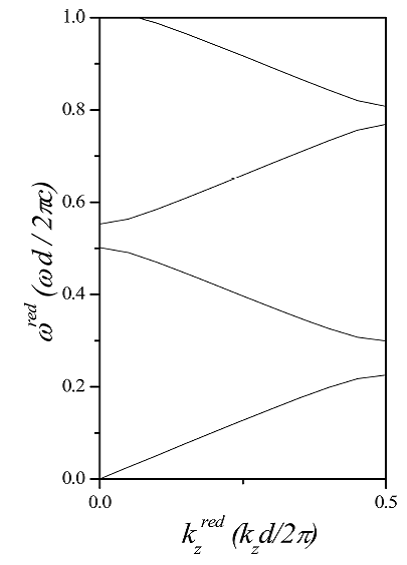
Figura 3. Se muestra la estructura de bandas con 201 ondas planas.

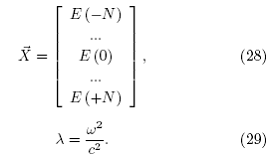
En la Figura 3 presentamos la estructura de bandas del sistema. En el eje X graficamos el vector de onda reducido y en el eje Y la frecuencia reducida. Observa­mos que existen cuatro brechas energéticas (BEP) en el intervalo de energia entre O y 1. Las ondas electromagne­ticas con valores de energia dentro de la BEP no pueden propagarse en el interior del cristal. En el Apéndice 3 mostramos el programa que hemos usado para realizar esta figura. Estos programas pueden ser de utilidad pa­ra investigadores experimentales que realizan diferentes estudios de aplicación de cristales fotónicos. Veamos un ejemplo. Para realizar la amplificación de serial luminis­cente en la presencia un cristal fotónico unidimensional [11] es necesario optimizar los parametros de red de óxi­do de silicio. La búsqueda (le la. amplificación de la serial

luminiscente puede ser un camino para la elaboración de láseres basados en cristales fotónicos.

5. CONCLUSIONES

Hemos realizado una exposición detallada de cuatro puntos importantes del Metodo de Ondas Planas para la obtención de Bandas de Energía Prohibida en crista­les fotónicos en una dimensión. En primer lugar, Mos­tramos la utilización de series de Fourier para describir una función periódica. En segundo lugar, tomamos la ecuacion de onda definida en el espacio real y mediante la sustitución de las series de Fourier del inverso de la función dieléctrica y el campo electromagnético obtene­mos la ecuación de valores propios definida en el espacio de Fourier. En tercer lugar, ilustramos la obtención de una ecuación matricial mediante la expansión de la ecua­ción de valores propios. Por último, presentamos codigos computacionales en lenguaje Matlab que permiten al es­tudiante tomar confianza en el cálculo de expansión de series de Fourier y cálculo de bandas.

A nuestro conocimiento no existe otro reporte en cas­tellano donde se detalle el Metodo de Ondas Planas de la forma en que hemos enfocado este trabajo. Considera­mos que nuestra exposición es de utilidad a los estudian­tes que inician en el estudio de Bandas de Energía Prohi­bida no solamente para cristales fotónicos, sino tambien para el estudio de otros medios periódicos.

6. AGRADECIMIENTOS

Este trabajo fue finaciado por el proyecto CONACYT-60897. RAG agradece una Beca-Tesis de Maestria. Agradecemos a "PROMEP-2005" por financiamento especial.

7. APÉNDICE 1

La ec. (5) puede se puede escribir como

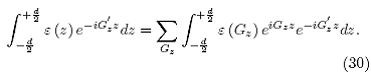
Podemos definir la integral en el lado derecho como І1:

8. APÉNDICE 2

clear

ip = 20;

d = 100.0d-10;

a = d/2;

b = d/2;

f = a/d;

el = 5.52;

e2     2.1316;

G = 2*pi/d;

ic = 1;

for n = -ip:ip

Gz = n*G;

GzV(ic) = Gz;

if n == O

epsiV(ic) = 1/e1+ r(l/e2-1/e1);

else

epsiV(ic) = f*(1/e2-1/e1)* (sin(GzV(ic)*a/2))/(GzV(ic)*a/2);

end

ic = ic + 1;

end

iz = 1;

for z = 0:d/500:d

zV(iz) = z;

for n=-ip:ip

cpsi(iz) =cpsi(iz) + cpsiV(ic)*exp(i*GzV(ic)*z);

subplot(2,1,1);plot(GzV,epsiV) subplot(2,1,2);plot(zV/d,epsi)

9. APÉNDICE 3

clear

ip = 0;

                   d = 100.0d-10;

a = d/2;

b = d/2;

f = a/d;

el = 5.52;

e2 = 2.1316;

G = rpi/d;

ikz=1;

for kz = O : 0.1*(pi/d) : pi/d

ir=1;

ic=1;

for n=-ip:ip

Gzn=Gsn;

for m.-ip:ip;

Gzm=G*m;

Gzn_rn Gzn - Gzm;

if n == m

mu = 1/e1+ f*(1/e2-1/e1);

else

A(ir,ic)=mu*(kz+Gzm)2;

ic=ic+1;

end% m

ic=1;

ir=ir+1;

end% n

e = eig(A);

w = sort(e);

Vkz(ikz)             kz*(d/(2*pi));

Vw1(ikz) = sqrt(abs( w(1)))*(d/(2*pi)); Vw2(ikz) = sqrt(abs( w(2)))*(d/(2*pi)); Vw3(ikz) = sqrt(abs( w(3)))*(d/(2*pi)); Vw4(ikz) = sqrt(abs( w(4)))*(d/(2*pi)); Vw5(ikz) = sqrt(abs( w(5)))*(d/(2*pi)); ikz = ikz+1;

end

REFERENCIAS

1. Yablonovitch E., Phys. Re^y. Lett.58, 2059, 1987.

2. Archuleta-Garcia R.,"Heteroestructuras de cristal fotóni­co", Tesis de Maestría, Universidad de Sonora, 2007.

3. Yablonovitch E., Gmitter T.J., Phys. Re^y. Lett. 63, 1950, 1989.

4. John R., Ftangarajan R., Phy.s. Re^y. B 38, 10101, 1988. Economou EN., Zdetsis A., Phys. Re^y. B. 40, 1334

5. Leung K.M., Liu Y.F., Phys. Re^y. Lett. 65, 2646, 1990.

6. Ho K.M., Chan C.T., Soukoulis C.M., Phys. Re^y. Lett. 65, 3152, 1990.

7. Sozuer H.S., Haus J.W., Phys. Re^y. B 45, 13962, 1992.

8. Ramos-Mendieta F., Halevi P., J. Opt. Soc. of America B 14, 370, 1997.

9. Agarwal V., Del Rio J.A., App/. Phys. Lett. 82, 1512, 2003.