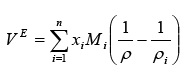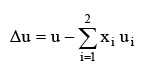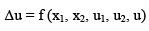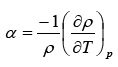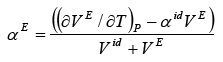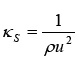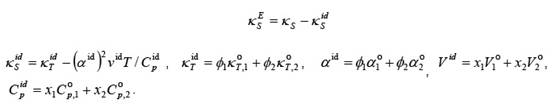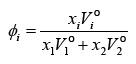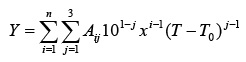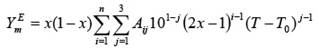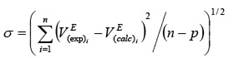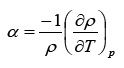INTRODUCCIÓN

Conocer las propiedades físicas de las mezclas de líquidos no electrolitos es esencial para la industria química que involucra procesos de separación y purificación de compuestos procedentes del petróleo, el alquitrán de hulla, y también de productos sintéticos. Existe una gran cantidad de compuestos orgánicos en estado líquido a temperaturas próximas a la del ambiente, y considerando todas sus posibles combinaciones, el número de sistemas que son objeto de estudio es enorme. El conocimiento del proceder y las propiedades termodinámicas de esas mezclas han llevado a un aumento y desarrollo de las investigaciones no solo a nivel experimental, de donde surgieron una multitud de bases de datos y bibliografía especializada, sino a nivel teórico con el desarrollo de modelos y/o correlaciones que permiten reducir la siempre costosa y compleja experimentación. Con el avance de las investigaciones y estudios se ha pretendido, aunque no siempre con éxito, desarrollar modelos teóricos predictivos para poder satisfacer las necesidades, tanto del conocimiento científico como del campo de los procesos industriales. El objetivo ideal sería lograr que el modelo de correlación conlleve una base teórica que pudiera reproducir a través de un determinado procedimiento de cálculo el comportamiento de los sistemas fluidos.

Se dispone en la literatura de modelos para describir el comportamiento termodinámico de sistemas multicomponentes. Esos modelos predicen el comportamiento de estos sistemas a partir de datos de sistemas binarios. Se los identifica como modelos geométricos, y se pueden mencionar entre otras, las expresiones empíricas propuestas por Redlich y Kister (Redlich O. y Kister A. T. 1948 ¹). La exactitud con que ciertos modelos predicen el comportamiento termodinámico de las mezclas depende fundamentalmente de las consideraciones realizadas sobre las ecuaciones de estado, el conocimiento de las fuerzas intermoleculares y de la dependencia con la temperatura y con la presión.

Este trabajo de investigación fue proyectado para efectuar un estudio experimental y teórico de un conjunto de propiedades termodinámicas para poder explicar las interacciones de ésteres con nitrilos de cadena corta, en particular las mezclas binarias formadas por propanonitrilo, propanoato de metilo y propanoato de etilo. La polaridad y tamaño de las moléculas involucradas en las mezclas tienen un efecto dominante en las magnitudes de las propiedades termodinámicas de exceso y en el tipo y alcance de las interacciones moleculares. Por tanto, para interpretar el tipo de interacciones moleculares presentes en estas mezclas y poder describir el comportamiento de las propiedades termofísicas se trazó un plan consistente en estudiar primero experimentalmente y luego en forma teórica los sistemas mencionados. Con los medios que se dispone en el laboratorio de Fisicoquímica de la Facultad de Ingeniería, de la Universidad Nacional del Comahue se determinaron experimentalmente las propiedades termofísicas (densidades y velocidades del sonido) para los líquidos puros y las mezclas. Luego se realizaron los cálculos de las magnitudes de exceso correspondientes para obtener, mediante el análisis e interpretación de los resultados, un mejor conocimiento y comprensión de las interacciones que suceden en este tipo de disoluciones; además de la concentración, la temperatura y la presión.

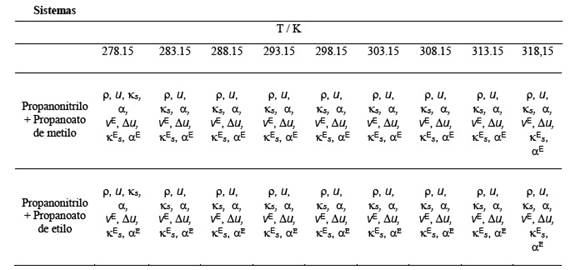
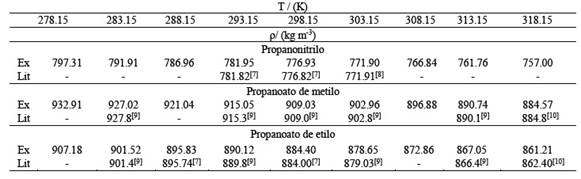
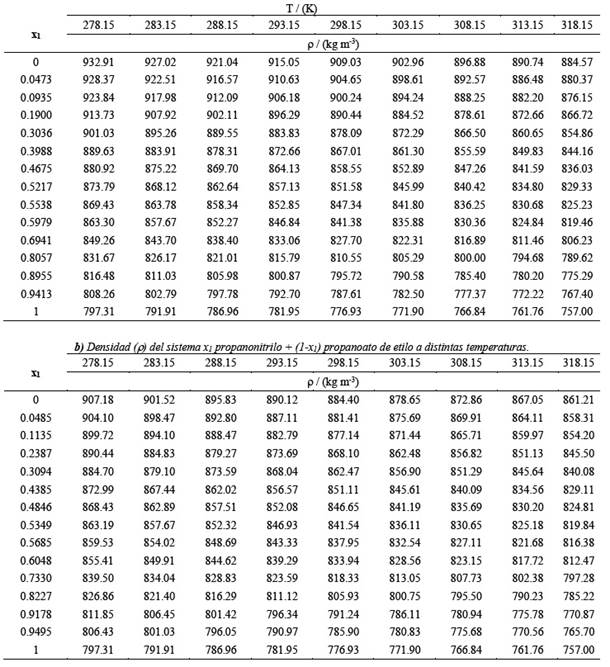
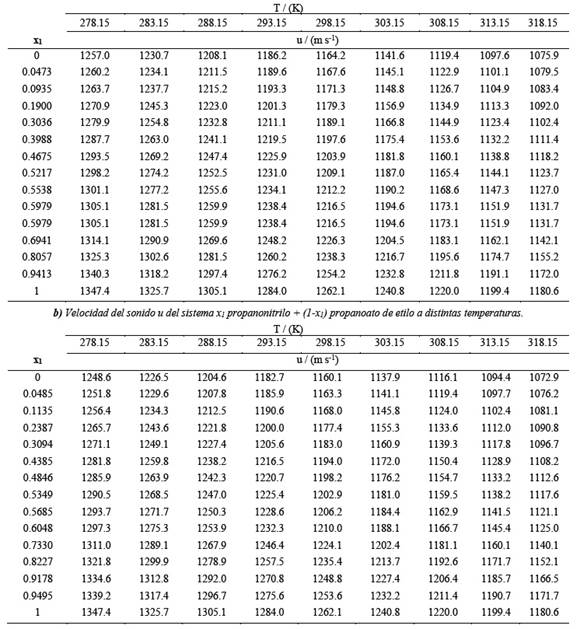
La densidad y la velocidad del sonido de las mezclas líquidas binarias de propanonitrilo +propanoato de metilo y propanonitrilo + propanoato de etilo se midieron en todo el espectro de fracciones molares, en un rango de temperaturas entre 278.15 K y 318.15 K a intervalos de 5 K, la presión de trabajo fue la presión atmosférica Tabla 1. Una vez obtenidos los datos experimentales, se procedió a la correlación matemática de los mismos, utilizando los modelos y ecuaciones más significativos/as que se ofrecen actualmente en la literatura. Los valores teóricos de la velocidad del sonido se calcularon para las mezclas binarias indicadas, en todo el rango de composiciones y a nueve temperaturas (278.15 a 318.15 K, cada 5 K). Se utilizó la relación empírica de Nomoto (Nomoto O., 1958 ²,³), la relación de mezcla ideal de Van Dael (Van Dael W., 1975 ⁴) y el modelo de velocidad media del sonido respecto al tiempo de un impulso de Ernst et al. (Ernst S., Glinski J., B., y Jezowska-Trzebiatowska, 1979 ⁵).El objetivo de esta parte del estudio, es mostrar la aplicación de los modelos predictivos para la velocidad ultrasónica indicados anteriormente, y comparar la eficacia de estos métodos en el cálculo del "exceso" de la velocidad de sonido para las mezclas binarias de líquidos estudiadas, y determinar cuál de los tres modelos teóricos predice mejor (con menor error) la velocidad del sonido en los sistemas estudiados experimentalmente.

Tabla 1 Sistemas binarios estudiados a distintas temperaturas, propiedades medidas y derivadas 

RESULTADOS Y DISCUSION

A partir de las medidas de densidad de mezclas de composición conocida, Tabla 2, es posible calcular el volumen molar de exceso, V^E, de mezclas binarias con la siguiente ecuación ⁶:

x_i es la fracción molar del componente i en la mezcla, Mi es el peso molecular del componente i, ρ es la densidad de la mezcla, ρ_i la densidad del componente i, y n es el número de componentes de la mezcla.

A partir de los datos de velocidad del sonido, Tabla 3, se puede calcular la desviación de la velocidad del sonido con la siguiente expresión ⁶:

x_i es la fracción molar del componente i, u es la velocidad del sonido de la mezcla, u_i es la velocidad del sonido del componente i, y n es el número de componentes de la mezcla.

Tabla 2 a) Densidad (() del sistema x1 propanonitrilo + (1-x₁) propanoato de metilo a distintas temperaturas 

Para una mezcla binaria (i=2) como las presentadas en este trabajo, puede expresarse como:

Los errores parciales pertenecientes a cada una de las cantidades señaladas en la ecuación son para la fracción molar 0.0001 unidades, y para la velocidad del sonido de 0.05 m s^-1. De lo anterior, se puede decir que el error para la desviación de la velocidad del sonido se estima en ± 0.1 m s^-1.

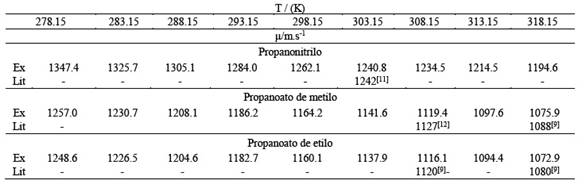
Tabla 3 a) Velocidad del sonido u del sistema x1 propanonitrilo + (1-x1) propanoato de metilo a distintas temperaturas 

El coeficiente de expansión térmica α se puede obtener a partir de la ecuación de ajuste de las densidades ρ= ρ(T) por derivación analítica de dicha ecuación respecto de la temperatura con la ecuación ⁶:

El coeficiente de expansión térmica isobárico de exceso, α^E, es posible calcularlo a partir de los volúmenes de exceso a diferentes temperaturas usando la ecuación ⁶:

La compresibilidad isoentrópica, definida por ⁶:

Es una función de la densidad y de la velocidad del sonido. El error estimado para Ks es del orden de ± 0,1.10^-12 Pa^-1. Se puede calcular la compresibilidad isoentrópica de exceso K^E _S a partir de la siguiente expresión ⁶:

C^o _p.1 y C^o _p.2 son las capacidades caloríficas molares isobáricas de los componentes 1 y 2, x₁ y x₂ son las fracciones molares de los componentes 1 y 2; ϕ₁ y ϕ₂ las fracciones en volumen de los componentes 1 y 2, definidas por ⁶:

Las densidades, velocidades del sonido, compresibilidades isoentrópicas, y coeficientes de dilatación cúbica se ajustaron para cada sistema a un polinomio del tipo mostrado en la siguiente expresión ⁶:

Donde Y es la propiedad, x es la fracción molar, Aij son los coeficientes de ajuste, T es la temperatura y T₀ es una temperatura de referencia que en todos los casos es la más baja a la que se conoce una propiedad. Con la ecuación polinomial como la ecuación de Redlich y Kister ^{1 .)} se ajustaron todas las magnitudes de exceso:

. 

Donde Y^E _m representa V^E, α^E, (u, o K^E _S; x es la fracción molar del componente 1, A_ij son los coeficientes de ajuste. En todos los casos los valores de los coeficientes se han obtenido mediante el método de mínimos cuadrados con dos variables de ajuste, temperatura y composición Tablas 4. y 5; la desviación estándar σ definida como ^{6 .)}:

. 

n el número de datos experimentales y p el número de coeficientes de la ecuación se muestra en las Tablas 4 y 5.

Tabla 4 Coeficientes de ajuste, (Aij), desviación estándar de los coeficientes, σ(Aij), y desviación estándar de la estimación σ(V^E), σ(Δu), σ(K_S ^E) y σ(α^E), del sistema propanonitrilo + propanoato de metilo. 

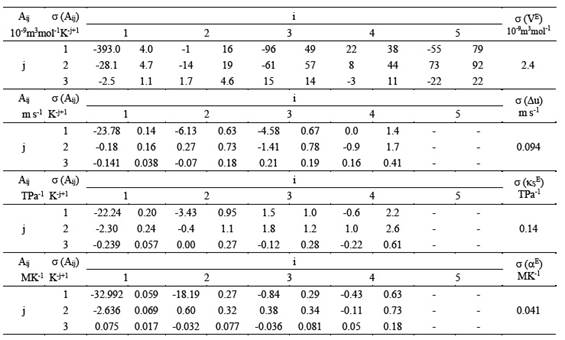
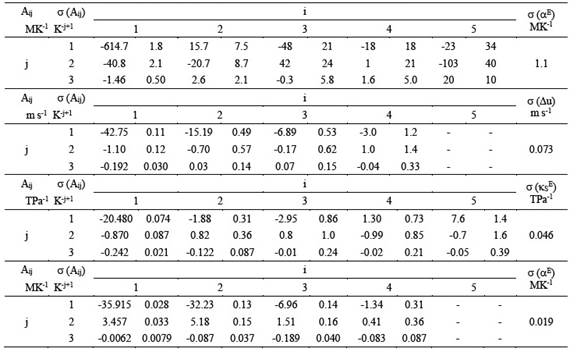
Tabla 5 Coeficientes de ajuste. (Aij). desviación estándar de los coeficientes. σ(Aij). y desviación estándar de la estimación. σ(V^E). σ(Δu). σ(K_S ^E) y σ(α^E). del sistema propanonitrilo + propanoato de etilo 

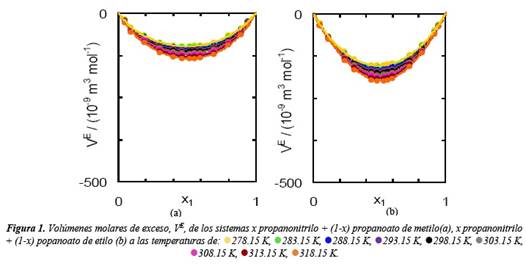
Hacemos un análisis descriptivo de los resultados obtenidos para las propiedades termodinámicas estudiadas, y en base a ello interpretaremos los tipos de interacciones moleculares que se establecen entre los componentes durante el proceso de mezcla. Es conveniente estructurar el análisis de acuerdo con la naturaleza de las propiedades y la dependencia de las mismas con la temperatura, composición, y tamaño molecular. Primero analizamos el volumen molar de exceso y su dependencia con la temperatura y la composición. Los sistemas binarios estudiados, propanonitrilo + propanoato de metilo y propanonitrilo + propanoato de etilo, presentan valores negativos de esta propiedad para todas las fracciones molares. Este comportamiento puede observarse en la figura 1 (a) y (b) para T=298.15 K, donde se ven también los volúmenes de exceso V^E para una determinada fracción molar x₁ = 0.5 a esa temperatura, en función de la longitud en la cadena carbonada del éster RCOOR’ para esos sistemas binarios. Se aprecia claramente una tendencia decreciente de la propiedad estudiada, o sea, con el tamaño creciente de las moléculas del éster en el sentido de R’ los valores negativos aumentan. Entre los factores que hacen aumentar el valor negativo del volumen molar de exceso, está el hecho de que las interacciones que ocurren entre moléculas distintas son más fuertes que las presentes entre moléculas iguales. La interacción dipolo-dipolo, causada por el fuerte carácter polar del grupo carbonilo del éster, y las moléculas de nitrilo también podría realzar éstos valores negativos.

. 

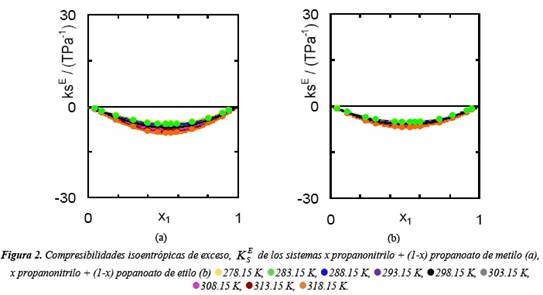
Analizamos las compresibilidades isoentrópicas de exceso y su dependencia con la composición y la temperatura para las mezclas propanonitrilo + propanoato de metilo, propanonitrilo + propanoato de etilo. Esta propiedad presenta valores negativos para todo el rango de concentración y para todas las temperaturas analizadas como se muestra en la figura 2 (a) y (b). En todos los casos, estos valores son más negativos al aumentar la temperatura. Se observa que esta variación con la temperatura es menos significativa al aumentar el número de átomos de carbono del éster. Este comportamiento pudo observarse para T=298.15 K, donde se vieron las compresibilidades isoentrópicas de exceso para una determinada fracción molar, x₁ = 0.5 a esa temperatura en función de la longitud en la cadena carbonada del éster RCOOR’ para esos sistemas binarios. Se aprecia claramente una tendencia creciente de la propiedad estudiada, es decir, con el tamaño creciente de las moléculas del éster en el sentido de R’, los valores negativos disminuyen. Para las mezclas binarias de propanonitrilo y esteres los valores de K^E _S son moderadamente negativos, lo que indica que el efecto combinado de interacciones específicas y contribuciones de volumen libre es relativamente grande comparado con las interacciones de dispersión entre las moléculas participantes.

Modelos predictivos para la Velocidad del sonido

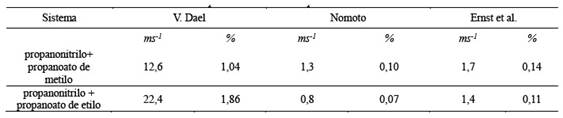
El objetivo de esta parte del estudio es mostrar la aplicación de los modelos predictivos para la velocidad ultrasónica de: Nomoto (Nomoto O. (1958); Nomoto, O. (1953)), la relación de mezcla ideal de Van Dael (Van Dael, 1975) y el modelo de velocidad media del sonido respecto al tiempo de un impulso de Ernst et al (Ernst, S. J.; Glinski, B. and Jezowska-Trzebiatowska, 1979) y comparar la eficacia de estos métodos más utilizados en el cálculo del "exceso", entendido como las desviaciones de los valores experimentales respecto de los teóricos. Se presenta una comparación de los valores que surgen de la aplicación de los modelos con los valores obtenidos experimentalmente y luego se determina cuál de los tres modelos teóricos predice mejor (con menor error) la velocidad del sonido de los sistemas estudiados experimentalmente. Las velocidades ultrasónicas calculadas junto con las velocidades experimentales, el porcentaje de error en las predicciones respecto de los valores experimentales, y las desviaciones de los valores experimentales respecto de los teóricos u_EXP. - u_CALC., para cada fracción molar, y a 298,15 K, se muestran en las Tabla 6

. 

Tabla 6 Comparación de las desviaciones máximas de velocidades del sonido calculadas por los modelos estudiados, respecto de los valores experimentales 

También se puede ver, en las figuras 3 y 4 una comparación entre valores teóricos y experimentales de las velocidades del sonido (u) de los sistemas binarios estudiados a nueve temperaturas para todo el rango de concentraciones.

Se observa para estas mezclas, que la ecuación de Van Dael muestra resultados de menor valor que los experimentales, para todas las temperaturas y fracciones molares. También se ve que la predicción de este modelo se aparta de los resultados experimentales a medida que aumenta el número de átomos de carbono del éster. Para estos sistemas con la aplicación de la relación empírica de Nomoto, y el modelo de velocidad media del sonido de Ernst et al se obtuvieron resultados análogos entre sí con valores levemente inferiores a los experimentales para todas las temperaturas y fracciones molares, como lo indican las trazas continuas de la figuras 3 y 4, como consecuencia de lo anterior las desviaciones de los valores experimentales respecto de calculados con estos modelos, u_EXP-u_CALC, a 298.15 K dan curvas simétricas levemente positivas como se muestra en las gráficas de la figura 5 (a) y (b). Aunque los valores calculados con los tres modelos se desvían de los datos experimentales de la velocidad, los datos obtenidos de Nomoto y de Ernst están en mejor acuerdo con la velocidad experimental que la relación de mezcla ideal de Van Dael.

La pregunta pendiente es cuál de los dos modelos, el de Nomoto o el de Ernst, es mejor, en el sentido de menores desviaciones de la velocidad del sonido entre valores experimentales respecto de los teóricos u_EXP-u_CALC. Lo importante en los sistemas analizados es que los signos de las desviaciones, prácticamente son los mismos para estos dos modelos propuestos.

La predicción de las velocidades del sonido de los sistemas produjo buenos resultados con dos de los tres modelos aplicados, y para todas las temperaturas estudiadas, como se muestra en las figuras 4 y 5. Las predicciones obtenidas con los modelos de Nomoto y de Ernst concuerdan mejor con los valores experimentales de la velocidad que la relación de Van Dael para las mezclas propanonitrilo + propanoato de metilo y propanonitrilo + propanoato de etilo.

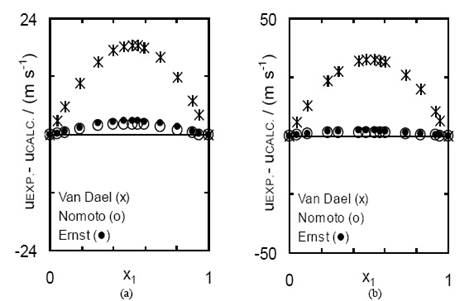
Figura 5 Desviaciones de la velocidad del sonido, valores experimentales respecto de calculados con los modelos de predicción, mediante la relación de mezcla ideal de Van Dael (x), la relación empírica de Nomoto (o), y el modelo de velocidad media de Ernst uEXP - uCALC, para cada fracción molar, y a 298.15 K de los sistemas x propanonitrilo + (1-x) propanoato de metilo(a) y x propanonitrilo + (1-x)propanoato de etilo (b). 

El análisis de las desviaciones observadas entre los valores teóricos de velocidad del sonido y los valores experimentales debería ser tratado como pruebas corroborativas de las interacciones moleculares que ocurren entre las moléculas componentes en estos sistemas binarios.

De todo lo anterior se puede indicar: La ecuación de Van Dael describe la dependencia de u= f(x) mucho peor que las otras dos ecuaciones. La ecuación de Ernst es la más simple, también en el sentido de las suposiciones. Las ecuaciones de Nomoto y de Ernst se recomiendan casi igualmente para las discusiones de las velocidades del sonido en mezclas líquidas binarias.

EXPERIMENTAL

Productos utilizados

Todos los líquidos empleados, propanonitrilo, propanoato de metilo, propanoato de etilo, antes de su uso fueron deshumidificados con tamices moleculares Fluka 4A y se desgasificaron mediante un baño de ultrasonido. Las mezclas líquidas se prepararon por pesada, utilizando una balanza electrónica autocalibrable, monoplato, Mettler AE-240 (precisión de 1·10^-8 kg.), el error en la fracción molar se estima en 1·10^-4. En las Tablas 7, 8 y 9 se muestran los líquidos empleados en el trabajo experimental, su procedencia, la pureza y las propiedades de los mismos.

Tabla 7 Procedencia y pureza de los líquidos utilizados 

Tabla 8 Densidades ρ de los líquidos puros a la temperatura T 

Tabla 9 Velocidades del sonido u de los líquidos puros a la temperatura T. 

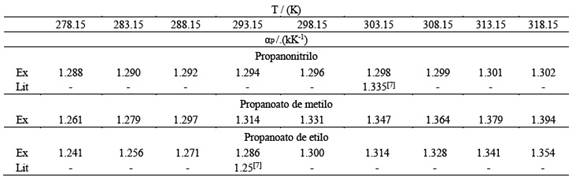
El coeficiente de dilatación cúbica α_p se obtuvo a partir de la ecuación de ajuste de las densidades ρ= ρ(T) ⁶, por derivación analítica de dicha ecuación respecto de la temperatura, haciendo uso de la definición de αp, como se muestra en la siguiente ecuación..

. 

Una comparación de los datos de la Tabla 10 con valores de la bibliografía nos revela una buena consistencia entre ambos.

Tabla 10 Coeficientes de dilatación cúbica αp de los líquidos puros a la temperatura T 

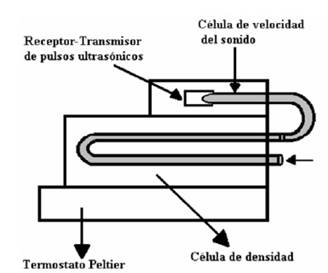
Dispositivos Experimentales

La densidad y la velocidad del sonido de los componentes puros y sus mezclas se midieron con un equipo Anton-Paar DSA 48. Este equipo permite realizar de forma automática las medidas de la densidad y velocidad del sonido de la mezcla y/o productos puros, a varias temperaturas en una misma muestra. Para ello, posee dos células conectadas en serie, una para cada propiedad a medir, según se muestra en el esquema de la figura 6. La célula de medida de densidad consiste en un tubo de vidrio con forma de U, rodeado por una camisa también de vidrio; el conjunto está situado dentro de un recinto termostático de cobre cuya temperatura puede controlarse mediante unos elementos Peltier. El recinto termostático está relleno de un gas de alta conductividad térmica, para facilitar el mantener la temperatura constante del tubo en U en cada medición. Para efectuar la determinación experimental de densidad y velocidad del sonido se introduce la muestra líquida de manera tal que tanto la célula de la densidad como la de la velocidad del sonido queden completamente llenas. Para este fin se requiere un volumen de unos 2.3 cc de muestra. El aparato fue calibrado para cada temperatura de trabajo, la precisión en la medida de la densidad con este densímetro DSA-48 se estimó en un valor de ±1·10^-2 kg·m³ y para la velocidad del sonido en 0.05 m·s^-1.

Figura 6 Células de medida de la densidad y de la velocidad de sonido en el DSA-48. 

Las especificaciones técnicas del aparato son:

Intervalo de medida de densidad: 0-3000 kg·m^-3.

Intervalo de medida de velocidad del sonido: 1000-2000 m·s^-1.

Intervalo de temperatura: (263.15 - 343.15) K.

Precisión en la medición de la temperatura: ( 0.01 K.

Intervalo de presión: hasta 1 MPa

CONCLUSIONES

El volumen molar de exceso y su dependencia con la temperatura y la composición de las mezclas estudiadas propanonitrilo + propanoato de metilo, propanonitrilo + propanoato de etilo, presenta valores negativos para todas las fracciones molares; también a la T=298.15 K y para una determinada fracción molar x₁ =0.5 se aprecia claramente una tendencia decreciente de la propiedad estudiada con el tamaño creciente de las moléculas del éster en el sentido de R’ los valores negativos aumentan.

Las compresibilidades isoentrópicas de exceso y su dependencia con la composición y la temperatura para las mezclas propanonitrilo + propanoato de metilo, propanonitrilo + propanoato de etilo, presenta valores negativos para todas las fracciones molares; también pudo observarse a la T=298.15 K que esta propiedad para una determinada fracción molar, x₁=0.5.muestra una tendencia creciente, es decir, con el tamaño creciente de las moléculas del éster en el sentido de R’, los valores negativos disminuyen.

Para la predicción de la velocidad del sonido de los sistemas propanonitrilo + propanoato de metilo, propanonitrilo + propanoato de etilo con los modelos propuestos por Nomoto, y Ernst et al, los datos obtenidos están en mejor acuerdo con la velocidad experimental que los obtenidos con el modelo de Van Dael. Aunque los valores calculados con los tres modelos se desvían de los datos experimentales de la velocidad en los sistemas analizados, los signos de las desviaciones son prácticamente los mismos para los modelos propuestos por Nomoto y de Ernst. Por esto, se recomiendan a estos dos modelos casi por igual para las discusiones de las velocidades del sonido en mezclas líquidas binarias