Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
Compartir
Revista Boliviana de Química
versión On-line ISSN 0250-5460
Rev. Bol. Quim vol.32 no.5 La Paz dic. 2015
ARTÍCULOS ORIGINALES
Analysis of subspace clustering of molecules using chameleoclust, an evolutionary algorith
Análisis de 'subspace clustering' de moléculas utilizando Chameleoclust, un algoritmo evolutivo.
Sergio Peignier1,*, Heriberto Castañeta M.2
1Institut National de Recherche en Informatique et en Automatique INRIA, LIRIS-CNRS, UMR 5205, F-69621, Institut National des Sciences Appliquées de Lyon INSA-Lyon, Université de Lyon, France
2Department of Chemistry, Instituto de Investigaciones Químicas IIQ, Universidad Mayor de San Andrés UMSA, P.O. Box 303, Calle Andrés Bello s/n, Ciudad Universitaria Cota Cota, Phone 59122795878, La Paz, Bolivia, walimunata@gmail.com
*Corresponding author:sergio.peianier@insa-lyon.fr
Abstract
'Subspace clustering' has been successfully applied to different datasets, especially those characterized by a high dimensionality. However most of the traditional state-of-the-art 'subspace clustering' algorithms have usually many parameters that are hard to tune. Recently, it has been proposed a new evolutionary 'subspace clustering' that takes advantage of its evolvable genome structure to adapt to different datasets without any complicated parameters tuning. In this paper we apply this new technique to study 36 chemical molecules characterized by a large number of molecular descriptors in order to determine clusters with distinctive characteristics likely to be adsorbed on activated carbon BPL.
Keywords: Subspace clustering, Evolutionary algorithms, Chemical compounds, Descriptors, Adsorption.
Resumen
La técnica de minería de datos conocida como 'subspace clustering' ha sido aplicada exitosamente a diversos tipos de datos, especialmente a datos caracterizados por un gran número de dimensiones. Sin embargo muchos de los algoritmos de 'subspace clustering' clásicos poseen un gran número de parámetros y son difíciles de calibrar. Recientemente, fue propuesto un algoritmo evolutivo de 'subspace clustering', capaz de adaptar su genoma para lidiar con distintos datos sin necesidad de calibrar los parámetros. En este artículo aplicamos esta nueva técnica al estudio de 36 moléculas químicas caracterizadas por un gran número de descriptores moleculares con el fin de determinar clusters de moléculas con características peculiares, susceptibles a ser adsorbidos sobre carbón activado BPL.
INTRODUCCION
La técnica de minería de datos conocida como subspace clustering tiene por objetivo detectar clusters es decir grupos de puntos que comparten características similares y detectar al mismo tiempo el conjunto de descriptores o sub espacio que caracteriza a cada grupo o cluster. Los autores Patrikainen and Meila [1] describen esta técnica como «similarity examined under different representations», es decir «similitud examinada bajo diferentes representaciones». Esta técnica está particularmente adaptada para analizar datos caracterizados por una gran cantidad de descriptores o dimensiones [2], al limitar los impactos del fenómeno llamado «maldición de la dimensión».
La mayor parte de los algoritmos de "subspace clustering" poseen una gran cantidad de parámetros y son relativamente difíciles de calibrar y de adaptar a cada conjunto de datos para ser analizados. Recientemente, fue presentado un nuevo algoritmo evolutivo de 'subspace clustering' [3]. Este algoritmo, llamado Chameleoclust, posee una estructura genética capaz de evolucionar, con el objetivo de aprovechar un fenómeno llamado «evolución de la evolución» [4]. Gracias a este fenómeno, Chameleoclust puede adaptarse a diferentes conjuntos de datos sin tener que calibrar sus diferentes parámetros y aun así es capaz de obtener resultados comparables a los mejores resultados obtenidos por algoritmos clásicos de 'subspace clustering'.
Una de las maneras más comunes y prácticas de analizar y representar moléculas químicas en informática es mediante el cálculo de descriptores moleculares. Una molécula corresponde a un vector de valores, cada valor estando asociado a un descriptor característico. Esta representación permite entre otras aplicaciones, evaluar la relación entre la estructura y la actividad de dicha molécula (QSAR) [5,6]. Existen diferentes programas de cálculo de descriptores moleculares, la mayor parte de estos programas generan una gran cantidad de descriptores, lo que hace que cada objeto o molécula exista en un espacio con muchas dimensiones, tal es el caso del programa Dragon [7]. La técnica de 'subspace clustering', estando muy bien adaptada al análisis de datos con muchas dimensiones, es una excelente candidata para analizar este tipo de datos.
El objetivo de este trabajo es mostrar la utilidad de técnicas de 'subspace clustering' y en particular de Chameleoclust, en el análisis de moléculas químicas. El resto del artículo se organiza de la siguiente manera: En la sección siguiente se describe Chameleoclust, el algoritmo de 'subspace clustering' utilizado, así como los datos analizados, el tratamiento de estos y el protocolo experimental seguido. En la sección 3, se describen los resultados obtenidos. Finalmente se concluye el trabajo resumiendo los puntos centrales del mismo.
Metodología
La metodología seguida en la parte de cálculos se ha realizado de acuerdo a trabajos previos [9,10]. Todas las estructuras fueron preoptimizadas mediante el campo de fuerza molecular (MM+) seguido de cálculos semiempíricos, Parametric Method-3 (PM3) en el programa Hyperchem 6.03 [8], con un gradiente de cálculo de 0.01 kcal/Å para la optimización geométrica. Asi mismo, se calcularon varios descriptores moleculares de los tipos constitucional, topológico, geométrico, carga, GETAWAY (Geometry, Topology and Atoms-Weighted) y varios otros, utilizando el programa Dragon, generando alrededor de un millar de ellos. A los datos anteriores se añadió los descriptores químico-cuánticos como ser HOMO y LUMO calculada para cada molécula.
Datos utilizados
La tabla 1 muestra los valores del parámetro de Dubinin Radushkevich para el cálculo de volúmenes de adsorción de 36 moléculas.
Descriptores generados
Para la generación de descriptores se ha tomado el conjunto de moléculas de entrenamiento suceptibles a ser adsorbidos sobre carbón activado BPL [ 9,10] y calculado los descriptores usando el programa Dragon [7].
Chameleoclust: Un algoritmo evolutivo de 'subspace clustering'
Chameleoclust es un algoritmo evolutivo de 'subspace clustering' que incluye muchas características bio-inspiradas, tales como un genoma con longitud, organización de variables, elementos funcionales y no funcionales, así como operadores de mutación que permiten reorganizar el genoma tales como grandes duplicaciones, grandes deleciones y translocaciones. Estas características han sido inspiradas por formalismos de evolución experimental in silico [14, 15]. Gracias a su estructura evolutiva y flexible, Chameleoclust tiene la habilidad de generar un cantidad variable de clusters caracterizados por un número variable de dimensiones.
El genoma G de un individuo es simplemente una lista [g1,...,gi,...,gn] de tuplas : gi = <fi, ci, di, xi>, el primer elemento de la tupla fi ![]() {0, 1} indica si la tupla gi es funcional (fi = 1) o no (fi = 0), los otros elementos de la tupla ci
{0, 1} indica si la tupla gi es funcional (fi = 1) o no (fi = 0), los otros elementos de la tupla ci ![]() {1, . . . , cmax }, di
{1, . . . , cmax }, di ![]() {1,...,D}, xi
{1,...,D}, xi ![]() {j x xmax /1000 | j
{j x xmax /1000 | j ![]() {-1000, ... , 1000}} sirven para definir el fenotipo del individuo, es decir el modelo de 'subspace clustering' que encarna. El fenotipo de un individuo es un conjunto de puntos alrededor de los cuales se agrupan los datos analizados para formar los clusters, estos puntos son llamados core points. El número máximo de core points es igual a cmax. Un número específico c
{-1000, ... , 1000}} sirven para definir el fenotipo del individuo, es decir el modelo de 'subspace clustering' que encarna. El fenotipo de un individuo es un conjunto de puntos alrededor de los cuales se agrupan los datos analizados para formar los clusters, estos puntos son llamados core points. El número máximo de core points es igual a cmax. Un número específico c ![]() [1, cmax] identifica a cada core point. Cada elemento funcional <1,c,d,x> del genoma contribuye con un valor x a la localización del core point c en la dimensión d. Todas las contribuciones se suman para producir los core points.
[1, cmax] identifica a cada core point. Cada elemento funcional <1,c,d,x> del genoma contribuye con un valor x a la localización del core point c en la dimensión d. Todas las contribuciones se suman para producir los core points.
Una vez que los core points han sido producidos, se procede a agrupar los datos por ser analizados alrededor del core point mas adaptado. El algoritmo calcula la función de mismatch o desajuste ![]() (x,p) entre cada dato x y cada core point p. Esta función se calcula utilizando la medida introducida por Aggarwal et al., [15] llamada Manhattan Segmental Distance. Posteriormente, cada punto es asociado al core point que minimiza esta función. Finalmente se suman las medidas de adaptación entre cada dato y el core point al cual ha sido asociado y el valor opuesto a esta suma define la aptitud (fitness) del individuo o la calidad del modelo de 'subspace clustering'. Cada individuo produce un número de hijos en función de su aptitud. Mayor la aptitud mayor el número de hijos, el número de hijos es definido utilizando el método conocido como ranking exponencial. Cada hijo producido, sufre una serie de mutaciones, el número de mutaciones siendo proporcional a la longitud de su genoma. De esta manera se produce la siguiente generación de individuos. Este proceso se repite durante un determinado número de generaciones, hasta que las mejoras en los modelos producidos dejen de ser significativas.
(x,p) entre cada dato x y cada core point p. Esta función se calcula utilizando la medida introducida por Aggarwal et al., [15] llamada Manhattan Segmental Distance. Posteriormente, cada punto es asociado al core point que minimiza esta función. Finalmente se suman las medidas de adaptación entre cada dato y el core point al cual ha sido asociado y el valor opuesto a esta suma define la aptitud (fitness) del individuo o la calidad del modelo de 'subspace clustering'. Cada individuo produce un número de hijos en función de su aptitud. Mayor la aptitud mayor el número de hijos, el número de hijos es definido utilizando el método conocido como ranking exponencial. Cada hijo producido, sufre una serie de mutaciones, el número de mutaciones siendo proporcional a la longitud de su genoma. De esta manera se produce la siguiente generación de individuos. Este proceso se repite durante un determinado número de generaciones, hasta que las mejoras en los modelos producidos dejen de ser significativas.
Diferente pruebas realizadas utilizando datos reales y sintéticos, gracias al Framework establecido por Muller et al., [16], mostraron que Chameleoclust es capaz de adaptarse a diferentes tipos de datos sin tener que modificar y optimizar sus parámetros, obteniendo resultados comparables con los mejores resultados obtenidos por algoritmos clásicos de 'subspace clustering', cuyos parámetros fueron optimizados para cada tipo de datos. Se invita al lector a referirse el articulo [3] para conocer mayores detalles sobre el funcionamiento del algoritmo.
Unificando los modelos
Se realizaron r = 50 análisis independientes de los datos gracias a Chameleoclust, utilizando los parametros estándar y fijando el número máximo de clusters a cmax = 10. En cada uno de los análisis solo se conservó el modelo de 'subspace clustering' generado por el individuo con mayor aptitud. Posteriormente, se utilizaron el conjunto de los r = 50 modelos de clustering para realizar un modelo único.
Para poder unificar los modelos, se procedió a utilizar el algoritmo de consensus clustering llamado Cluster-based Similarity Partitioning Algorithm. Primeramente, este algoritmo calcula una matriz de similitud para cada uno de los modelos de clustering generado. La matriz de similitud es una matriz binaria NxN donde N es el numero de moléculas químicas analizadas, el valor Nij = 1 si las moléculas i y j están en el mismo cluster y Nij = 0 en el caso contrario. Una vez que han sido calculadas las matrices de similitud para cada uno de los r modelos, se procede a calcular la matriz de similitud global S. Esta matriz se calcula sumando las r matrices de similitud y dividiendo el resultado entre r. El valor Sij de la matriz puede interpretarse como la fracción de modelos de clustering para la cual las moléculas i y j están el mismo cluster. Una vez obtenida esta matriz, se puede extraer de ella un modelo de clustering jerárquico, Para obtener dicho modelo unificado utilizamos el método de Ward utilizando la correlación entre 2 moléculas como distancia. Esta matriz nos permite analizar dos puntos importantes:
En primer lugar nos permite obtener un modelo más robusto y preciso, ya que éste no fue obtenido debido a un único análisis, sino más bien debido a múltiples análisis independientes relacionados entre sí. Si dos moléculas i y j han sido puestas muchas veces en el mismo cluster a raíz de análisis independientes i.e. Sij elevado, esto significa que es muy probable que dichas moléculas están fuertemente relacionadas entre sí e inversamente, si i y j casi nunca se encuentran en el mismo cluster i.e. Sij bajo, esto significaría que es poco probable que exista una similitud entre dichas moléculas.
En segundo lugar esta matriz nos permite caracterizar la robustez del algoritmo, si cada uno de los análisis independientes revela modelos muy diferentes entre sí, esto se caracterizaría por un modelo único muy mal estructurado y poco claro, que se caracterizaría por una distribución casi gaussiana de los votos y los valores de las casillas serian muy similares entre sí.
RESULTADOS Y DISCUSION
Evolución de lafitness y de las estructuras genómicas y de los modelos generados
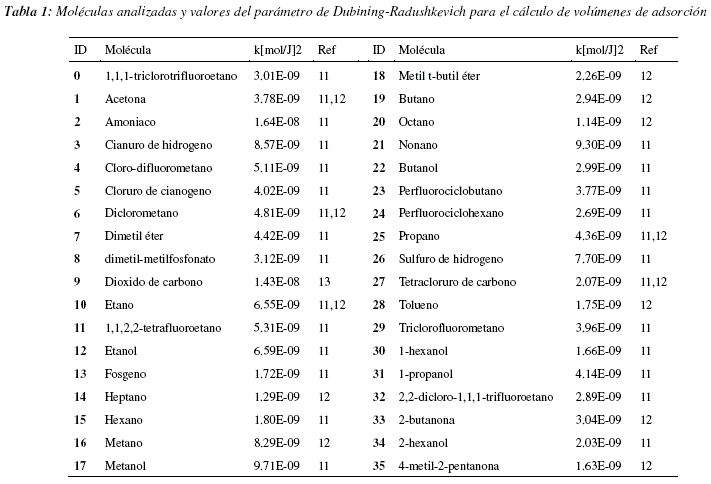
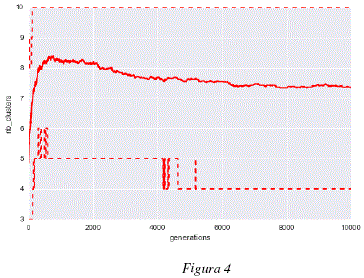
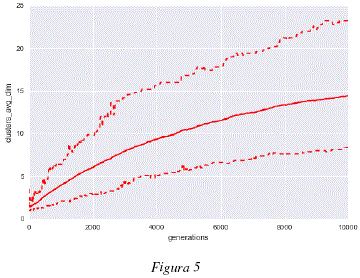
Como se puede observar en la figura 1, el promedio de la mejor aptitud (fitness) para cada uno de los análisis independientes crece, esto muestra que los individuos son capaces de generar modelos de 'subspace clustering' a partir de los datos utilizados, maximizando cada vez más, el grado de adaptación entre los core points producidos y los datos analizados. Las figuras 2 y 3 nos muestran que, mientras los organismos mejoran los modelos con cada generación, la estructura de los genomas de estos individuos evoluciona de igual manera para adaptarse a los datos. Podemos observar en las figuras 2 y 3 que los genomas convergen hacia una longitud de unas 250 tuplas y cerca de un 65% de tuplas funcionales. Los cambios en la estructura genómica se traducen también por un cambio en la estructura del modelo de 'subspace clustering' generado. Como podemos observar en las figuras 4 y 5, la estructura de los modelos de 'subspace clustering' generados por los individuos varia : la figura 4 muestra como el número de clusters generados tiende a crecer rápidamente durante las primeras generaciones y luego disminuye ligeramente y llega rápidamente a un punto más o menos estable; la figura 5 muestra como el número de dimensiones o de descriptores tomados en cuenta por los diferentes cluster, tiende a aumentar en promedio durante las 10000 generaciones, sin embargo este aumento es cada vez más lento. Si bien después de 10000 generaciones, las 3 curvas de las figuras 1, 2, 4 y 5 siguen evolucionando y no han alcanzado un valor estable, la evolución es bastante lenta, las mejoras en términos de aptitud (fitness) y los cambios en términos de estructura genómica y de estructura de modelo de 'subspace clustering' son ligeros.
Matriz de similitud y modelo global
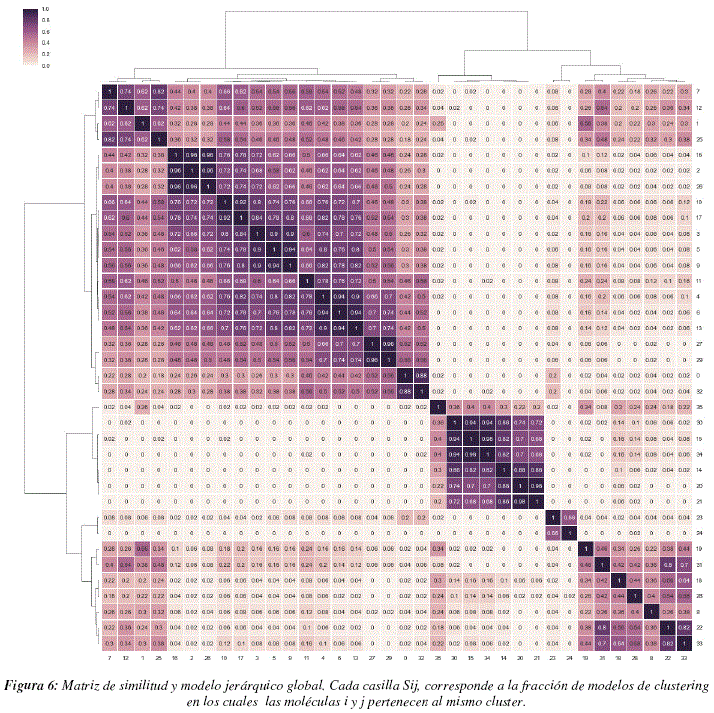
En la figura 6 se puede presenciar la matriz de similitud global generada gracias a cada uno de los modelos de 'subspace clustering' generados por los 50 análisis independientes realizados con el algoritmo Chameleoclust. El color de cada casilla de la matriz está relacionado con el valor que figura en la casilla, más elevado el valor, más oscura la casilla. Cada casilla Sij de la matriz corresponde a la fracción de análisis según los cuales las moléculas i y j estaban en un mismo cluster. Por definición esta matriz será simétrica. Como se puede apreciar claramente en la figura, la distribución de los valores de la matriz no parece ser gaussiana y las casillas pueden ser bastante diferentes entre sí. Existen bastantes casillas con valores muy bajos, es decir que las moléculas asociadas a esas casillas casi nunca fueron puestas en un mismo cluster, y existen también casillas con valores muy elevados, es decir que en buena parte de los modelos generados las moléculas en cuestión fueron puestas en un mismo cluster. Esta matriz posee una estructura bastante clara y está lejos de ser una matriz generada por un proceso meramente aleatorio. Esto demuestra que el algoritmo es robusto y aunque cada análisis produzca diferentes modelos, estos se parecen entre sí y transmiten una información similar.

En la parte superior y en el costado izquierdo de la matriz se puede presenciar el modelo jerárquico obtenido gracias a la matriz. La raíz del árbol o dendrograma, considera la existencia de un solo grupo que contiene todas las moléculas, posteriormente el árbol se va subdividiendo en ramas, la longitud de una rama corresponde a la distancia entre el grupo del cual se desprende la rama y el grupo que lo contiene. Si la rama es corta, significa que el nuevo grupo esta muy cerca del grupo más general. En la parte inferior y en el costado derecho de la matriz se encuentra el orden de las moléculas clasificadas.
Observando la estructura del árbol, se decidió analizar más detalladamente dos niveles de granularidad del modelo: el primer nivel asociado con la presencia de 3 clusters y el segundo con 5 clusters. Se decidió no focalizar a modelos con un mayor número de clusters, ya que, al no existir muchas moléculas, no tendría mucho sentido considerar muchos clusters ya que tendríamos muy pocos puntos por cluster y las observaciones no serían pertinentes.
Clusters y valores de adsorción
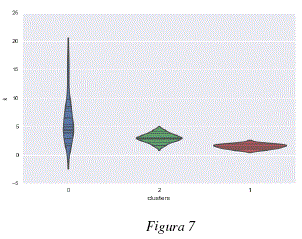
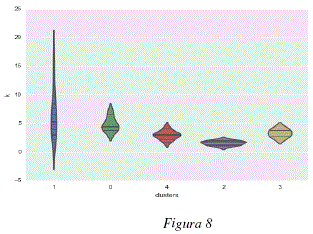
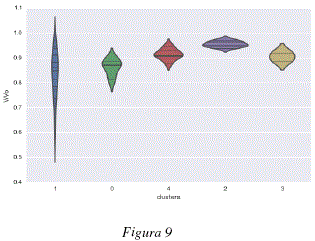
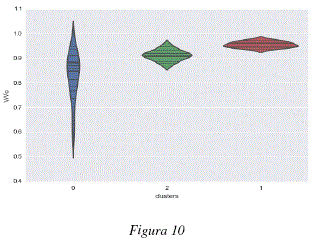
Dada la característica de los datos, se analizó el tipo de relación existente entre los clusters encontrados y las propiedades fisicoquímicas de las moléculas analizadas, específicamente, en lo que se refiere al parámetro de Dubinin Radushkevich para el cálculo de volúmenes de adsorción de gases y vapores. Las figuras 7 y 8 representan los valores de dicho parámetro k para cada una de las moléculas agrupadas en clusters. Las figuras 9 y 10 representan los valores de volumen adsorbido relativo de las diferentes moléculas analizadas agrupadas en clusters. Las figuras 7 y 9 representan respectivamente, los valores del parámetro k de Dubinin-Radushkevich y los volúmenes relativos adsorbidos para los 3 primeros clusters del modelo global; cada uno de estos clusters contiene las moléculas definidas en la tabla 2. Las figuras 8 y 10 representan respectivamente, los valores del parámetro k de Dubinin-Radushkevich los volúmenes relativos adsorbidos de los primeros 5 clusters del modelo global, estos 5 clusters contienen las moléculas especificadas en la tabla 3.
Como se puede observar en las figuras 7, 8, 9 y 10 los clusters encontrados están fuertemente correlacionados con los volúmenes relativos adsorbidos y los parámetros k de las moléculas que contienen. En las figuras 9 y 7 podemos ver que el cluster 1 tiene un parametro k más bajo y contiene moléculas con alto volumen relativo adsorbido, el cluster 2 tiene un parámetro k medio y contiene moléculas con adsorción media y el cluster 0 tiene un parámetro k más elevado y contiene moléculas más variadas y globalmente con un menor volumen relativo adsorbido. De la misma manera, los clusters representados en las figuras 8 y 10 están caracterizados por niveles diferentes de adsorción, el cluster 2 agrupa la moléculas con k bajo y un volumen relativo de adsorción elevado, el cluster 4 tiene un parámetro k medio-bajo y moléculas con adsorción media-alta, el cluster 0 contiene moléculas con un volumen de adsorción relativo medio-bajo y valores de k medio-altos y el cluster 0 contiene moléculas más variadas pero con parámetros k más elevados y volúmenes de adsorción relativos menos elevados, el cluster 3 es un caso especial y contiene dos moléculas bastante diferentes de las otras: el perfluorociclobutano y el perfluorociclohexano. Para poder calcular el volumen relativo adsorvido V/Vo se procedió a considerar en la ecuación de Dubinin-Radushkevich, una temperatura de 293.15K, una presión relativa P/Po = 0.1 y los parámetros de k especificados en el tabla 1.
![]()
![]()
![]()
Dimensiones utilizadas
La figura 11 muestra el número de veces que cada dimensión (columnas) es utilizada para describir cada una de las moléculas (líneas), al tener cada cluster en promedio unas 15 dimensiones, parece claro que cada modelo explora diferentes dimensiones y aun así da un resultado similar (robustez de la matriz de similitud), esto significa que la información contenida en los descriptores es bastante redundante. Al ser este espacio bastante redundante gracias a la correlación entre diferentes descriptores, la utilización de una técnica de 'subspace clustering' resulta ser bastante útil, ya que de esta manera se gana tiempo al considerar solo algunas de estas dimensiones, que contienen la información necesaria y al no tomar en cuenta dimensiones que no son portadoras de mayor información.
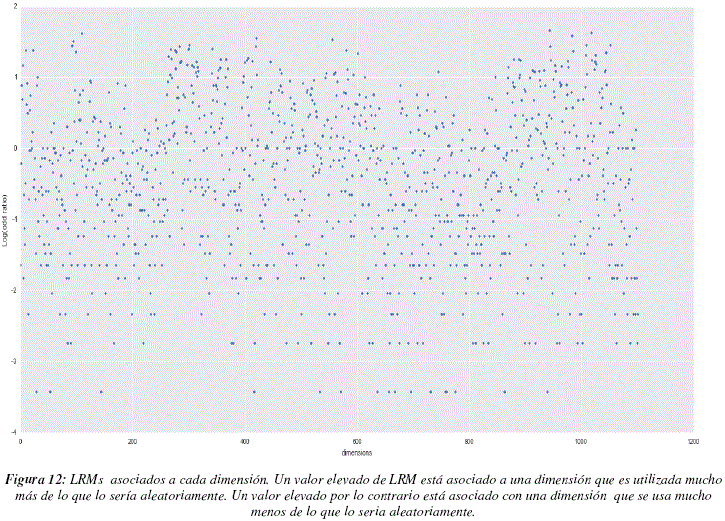
Analizando con mayor precisión las dimensiones que sirvieron para generar los modelos de 'subspace clustering', podemos ver que existen dimensiones que son más utilizadas que otras, lo cual nos muestra que existen algunos descriptores que permiten distinguir más claramente la estructura de los datos. Para poder detectar estas dimensiones más claramente, procedimos a calcular los logaritmos de razones de momios (LRMs) de cada dimensión. Los LRMs permiten comparar una distribución probabilística obtenida experimentalmente y una distribución teórica. Posteriormente, se extrae los valores de LRMs que reflejan una diferencia grande entre la distribución teórica y la distribución experimental, al no respetar estos valores la distribución teórica escogida y al ser por consiguiente portadores de información.
Estos valores se calculan estimando en primer lugar la probabilidad de que una dimensión sea tomada en cuenta por un modelo de 'subspace clustering' para clasificar un punto, esto se calcula sumando las veces que un modelo tomó en cuenta una dimensión en particular para clasificar un punto y dividiendo este valor por la suma de todos estos valores. En segundo lugar se debe decidir con que distribución teórica se comparara la distribución experimental, nosotros escogimos una distribución uniforme, ya que según esta distribución todas las dimensiones tendrían la misma probabilidad de ser utilizadas en un modelo de 'subspace clustering'. De esta manera, las dimensiones que sobresalgan, es decir cuya probabilidad de ser utilizada sea muy diferente de la probabilidad uniforme deben ser consideradas con una atención especial. Finalmente se calcula la diferencia de los logaritmos de las dos medidas para obtener el LRM.
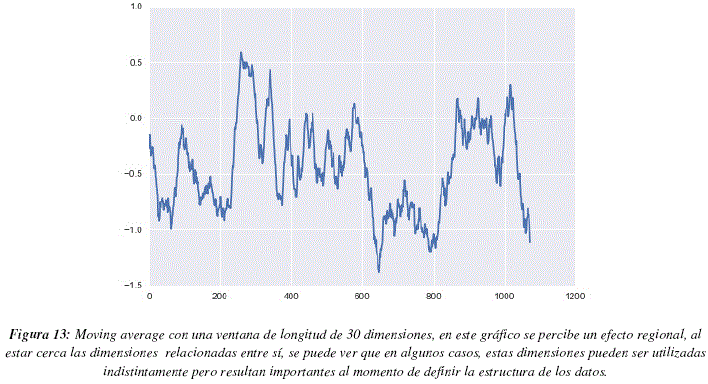
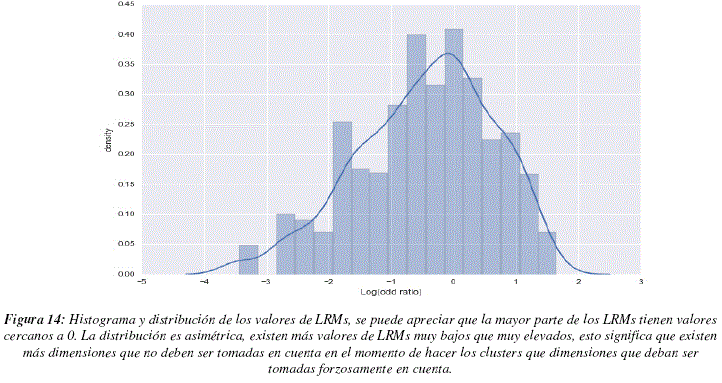
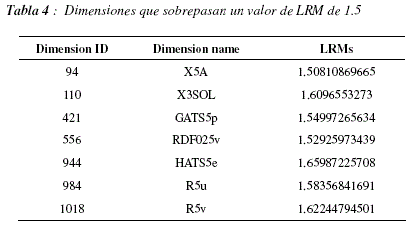
La figura 12 nos muestra los valores de LRMs para cada una de la dimensiones. Para analizar este gráfico debemos recordar que DRAGON, el programa que calcula los descriptores, acomoda lado a lado a los descriptores que caracterizan aspectos similares, teniendo en cuenta esta información podemos observar que suelen existir zonas en las cuales todos los descriptores tienen valores de LRMs elevados y zonas cuyos valores son globalmente más bajos, este punto es importante, ya que pueden existir descriptores similares que puedan ser utilizados de manera indistinta pero que deban ser tomados en cuenta en el modelo. Para poder observar el fenómeno mencionado aplicamos el método de moving average, con una ventana de longitud 30 dimensiones, los resultados pueden apreciarse en la figura 13. En este grafico podemos distinguir 3 regiones con LRMs más elevados (entre las dimensiones 250 y 300, cerca de la dimensión 350 y entre las dimensiones 1000 y 1050) y una región con LRMs particularmente bajos (entre las dimensiones 650 y 800). La figura 14 nos muestra la distribución de LRMs, podemos ver que la mayor parte de los valores tienen un valor de LRM cercano a 0, lo cual significa que no son muy diferentes de los valores que podrían ser obtenidos por un proceso aleatorio uniforme de selección de dimensiones. Sin embargo podemos ver también que existen más valores de LRMs que son muy bajos que valores de LRMs muy altos, esto significaría que hay más dimensiones que deben ser ignoradas que dimensiones que se tengan que tomar en cuenta a toda costa. La tabla 4 contiene las dimensiones que poseen valores de LRMs elevados, superiores a 1.5 para ser más específicos.
CONCLUSIONES
En este artículo se ha comprobado la utilidad de una nueva técnica evolutiva de 'subspace clustering', Chameleoclust, para el análisis de moléculas químicas según sus propiedades. Se ha podido verificar que este método es robusto y que los clusters producidos pueden ser de gran ayuda para analizar las propiedades fisicoquímicas de las moléculas en cuestión. Asimismo, se ha podido verificar la correlación encontrada entre los clusters y los valores del parámetro k de Dubinin Radushkevich, así como de los volúmenes de adsorción para las moléculas estudiadas. También se ha verificado el interés de esta técnica para encontrar las dimensiones y los descriptores que caracterizan la estructura de los datos. Un aspecto importante que se debe tomar en cuenta es que no fue necesaria una exploración paramétrica en la calibración del algoritmo de subspace clustering, ya que éste aprovecha la flexibilidad de su genoma para adaptarse a los datos a ser analizados, lo que hace que sea muy versátil y fácil de utilizar.
REFERENCIAS
1. Patrikainen, A., Meila, M., Comparing 'subspace clustering's. 2006, IEEE Transactions on Knowledge and Data Engineering, pp. 902-916. [ Links ]
2. Kriegel, H.P., Kroger, P., Zimek, A. 2009. ACM Transactions on Knowledge Discovery from Data, 3(1), 1,1-1, 58. [ Links ]
3. Peignier, S., Rigotti, C., Beslon, G. 'subspace clustering' using evolvable genome structure, 2015. In: Proc. of the ACM Genetic and Evolutionary Computation Conference (GECCO 2015). pp. 1-8 [ Links ]
4. Hindré, T., Knibbe, C., Beslon, G., Schneider, D. 2012. Nature Reviews Microbiology. [ Links ]
5. Kubinyi, H. 1997, Drug Discovery Today, 2, 457. [ Links ]
6. Carbó-Dorca, R., Amat, L., Besalú, E., Gironés, X., Robert, D. 2000, Journal of Molecular Structure: THEOCHEM, 504, 181. [ Links ]
7. Dragon, Talete srl. http://www.disat.unimib.it/chm. [ Links ]
8. Hyperchem, HyperCube. http://www.hyper.com. [ Links ]
9. Castañeta, H., Duchowicz, P., Castro, E., Vicente, J.L., Fernández, M. 2007, Rev. Bol. Quim., 24, 45. [ Links ]
10. Duchowicz, P., Castañeta, H., Castro, E., Fernández, M., Vicente, J.L. 2006, Atmospheric Environment, 40, 2929. [ Links ]
11. Wood G.O. 2001, Carbon, 39, 343. [ Links ]
12. Ye X., Qi N., Ding Y., Levan M.D. 2003, Carbon 41, 681. [ Links ]
13. Bickford, E.S., Clemons, J., Escallón, M.M., Goins, K., Lu, Z., Miyawaki, J., Pan, W., Rangel-Méndez, R., Senger, B., Zhang, Y., Radovic, L.R. 2004, Carbon 42, 1867. [ Links ]
14. Knibbe, C., Coulon, A., Mazet, O., Fayard, J.M., Beslon, G. 2007, MolecularBiology and Evolution, 24, 2344. [ Links ]
15. Crombach, A., Hogeweg, P. 2007, Molecular Biology and Evolution, 24, 1130. [ Links ]
16. Aggarwal, C.C., Wolf, J.L., Yu, P.S., Procopiuc, C., Park, J.S. 1999, Fast algorithms for projected clustering. In Proc. of the 1999 ACM SIGMOD Int. Conf. on Management of Data, pages 61-72. [ Links ]
17. Muller, E., Gunnemann, S., Assent, I., and Seidl, T. 2009, Evaluating clustering in subspace projections of high dimensional data. In Proc. 35th Int. Conf. on Very Large Data Bases (VLDB 2009), volume 2, pages 1270-1281 . [ Links ]












 uBio
uBio