Revista Boliviana de Química
versión On-line ISSN 0250-5460
Rev. Bol. Quim v.24 n.1 La Paz 2007
ARTÍCULO ORIGINAL
COMPROBACION EXPERIMENTAL DE DATOS PREDICHOS DE CAPACIDADES DE ADSORCIÓN MEDIANTE LA APLICACIÓN DE RELACIONES CUANTITATIVAS ESTRUCTURA-PROPIEDAD (QSPR) PARA C2H4.
Castañeta H.1*, Duchowicz P.2, Castro E.2, Vicente J. L.2, Fernández M.2
1Carrera de Ciencias Químicas. UMSA, La Paz-Bolivia, 2 Instituto de Investigaciones Fisicoquímicas Teóricas y Aplicadas, UNLP, La Plata-Argentina.
*Autor corresponsal: walimunata@gmail.com
ABSTRACT
The present article tries about the practical application of a lineal mathematical model obtained based on calculations of regression multivariable using the method of Substitution" (MR) to predict the constant k of Dubinin-Radushkevich of a group of 42 different molecules based on a group of training set of 36 molecules. From the constant k of the Ethylene (C2H4) predicted, the capacities of adsorption and the corresponding isotherms were calculated for 5 samples of activated coal. For the sample CAT that has certain catalytic properties was obtained isotherm of ethylene adsorption to several temperatures and for this same sample they were obtained isotherm of adsorption of several volatile substances, in the range of relative pressures (P/Po) between 0 and 0.2. The reached results allow to distinguish clearly among the different types of activated coal and it allows to decide which of them it is the most appropriate for its use to application effects in the purification of air, for example; also, the application of the pattern allows to obtain the isotherms of adsorption corresponding to each type of activated coal of characteristic similar to CAT or BPL, considering all the molecules for which its capacity of adsorption was predicted.
RESUMEN
El presente artículo trata acerca de la aplicación práctica de un modelo matemático lineal obtenido en base a cálculos de regresión multivariable usando el método de Reemplazo (MR) para predecir la constante k de Dubinin-Radushkevich de un conjunto de 42 moléculas distintas en base a un conjunto de entrenamiento de 36 moléculas. A partir de la constante k del Etileno (C2H4) predicha, se calcularon las capacidades de adsorción y graficaron las isotermas correspondientes para 5 muestras de carbón activado. Para la muestra CAT, que tiene ciertas propiedades catalíticas se obtuvieron isotermas de adsorción de etileno a varias temperaturas y para esta misma muestra se obtuvieron isotermas de adsorción de varias sustancias volátiles, en el rango de presiones relativas (P/Po) entre 0 y 0.2. Los resultados alcanzados permiten distinguir claramente entre los distintos tipos de carbón activado y permite decidir cuál de ellos es el más adecuado para su uso a efectos de aplicación en la descontaminación de aire, por ejemplo; además, la aplicación del modelo permite obtener las isotermas de adsorción correspondientes a cada tipo de carbón activado de características similares a CAT o BPL, considerando todas las moléculas para las cuales se predijo su capacidad de adsorción.
Key words: Adsorción, carbón activado, etileno, Dubinin-Radushkevich, isoterma, modelo, QSAR,QSPR.
INTRODUCCIÓN
En los últimos años, se han desarrollado un gran número de modelos matemáticos basados en los métodos de relaciones cuantitativas estructura-actividad (QSAR) y relaciones cuantitativas estructura-propiedad (QSPR) a fin de predecir propiedades fisicoquímicas y actividades biológicas de sustancias, como también, para predecir capacidades y energías de adsorción de distintos tipos de sólidos, y otras propiedades inherentes a las sustancias y materiales a partir de parámetros estructurales, electrónicos y/o topológicos [1-10].
RESULTADOS Y DISCUSION
La necesidad de contar con resultados de adsorción en el tiempo más corto posible, sin que ello implique realizar gastos dispendiosos y que abarque un gran número de sustancias, en particular, de aquellas que son empleadas en los procesos químicos y que representan un alto riesgo en su manejo, haciendo difícil las determinaciones experimentales, hace que los métodos mencionados se constituyan en una herramienta sumamente útil.
En la literatura, existen pocos trabajos relacionados a la aplicación del método QSAR en fenómenos de adsorción de gases y vapores sobre carbones activados. Se puede mencionar a Urano et al [11] quienes evaluaron las capacidades de adsorción de vapores orgánicos sobre siete distintos tipos de carbones activados, además de otro autores que realizaron trabajos referidos al tema [12,13]. Shaoying Qi, et al [14], estimaron capacidades de adsorción de sustancias sobre carbón activado de fibras (ACFs) empleando el modelo de adsorción de Dubinin-Radushkevich (ecuación 6), de la misma manera Nirmalkandam y Speece [C] para estimar el parámetro k, estos dos últimos modelos se describen con un solo descriptor, 1cn. Dobruskin V. Kh [15], desarrolló un modelo distinto al de QSAR, habiendo determinado inicialmente la textura del carbón, la cual es independiente del adsorbato empleado y de la temperatura de adsorción. Otro trabajo emprendido por Wu et al [16], es la aproximación del coeficiente de afinidad ß, por modelación que utiliza precisamente la ecuación de Dubinin-Radushkevich. Los coeficientes de afinidad fueron evaluados a partir de las isotermas de carbón activado Norit R1. Posteriormente, Wu et al [17] estudiaron la modelación para la influencia directa de propiedades fisicoquímicas de compuestos volátiles sobre la capacidad de adsorción de carbón activado. Fangmark I.E.[18] et al utilizaron las QSAR para predecir la capacidad de adsorción del carbón activado, denominándolas relaciones cuantitativas estructura-afinidad (QSAfR) [16,17]. Los autores estimaron la eficiencia de adsorción de carbón activado de vapores orgánicos (31 hidrocarburos clorados).
Las técnicas analíticas multivariables son utilizadas en conjunción con el diseño experimental estadístico para seleccionar un conjunto balanceado de compuestos y con ello, evaluar el progreso de la ejecución. En general, los modelos generados por los distintos autores apuntan a un solo objetivo, el de predecir las capacidades de adsorción; en ese tren se trata de elaborar el mejor modelo, aquel que prediga mejor los valores de las propiedades de adsorción.
El parámetro k de Dubinin-Radushkevich (D-R)
El uso de la ecuación de Dubinin-Radushkevich es simple y bastante práctico en la estimación de capacidades de adsorción de gases y vapores orgánicos. La cantidad adsorbida en volumen de gas por unidad de masa del adsorbente microporoso es V y la ecuación correspondiente es:
![]() (1)
(1)
k se define como:
![]() (2)
(2)
Donde: Vo es el volumen de microporos del adsorbente, V es el volumen de vapor adsorbido (cm3/g) , según la ecuación (1) el parámetro k se relaciona con la energía de adsorción característica Eo (kJ/mol) del adsorbente y el coeficiente de afinidad β.
Tabla 1. Volumen Vo (cm3/g) de microporos de muestras de carbón activado determinadas con el modelo de D-R.
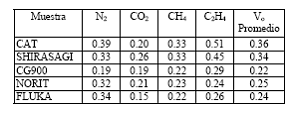
La ventaja de la presente propuesta para estimar capacidades de adsorción, radica en que se requiere, según la ecuación (1), obtener los parámetros k y Vo. El volumen de poros límite o volumen de microporos Vo del adsorbente es constante y se puede medir con un solo adsorbato. El parámetro k que depende tanto del adsorbente como del adsorbato es difícil medirlo y por lo tanto su valor debe ser suministrado por el modelo desarrollado.
Modelo QSAR/QSPR
Para la modelación de capacidades de adsorción de carbones activados, se han establecido las siguientes estrategias: búsqueda bibliográfica de capacidades de adsorción y parámetros β y k de la ecuación de Dubinin-Radushkevich y Dubinin-Astakhov de una gran cantidad de sistemas adsorbato-adsorbente que se encuentran al alcance de nuestra biblioteca virtual. Una vez obtenido los datos, se procedió a una selección rigurosa de los mismos, de las cuales, se eligió el carbón activado con más moléculas, es decir, carbón activado tipo BPL, granulado, microporoso y de superficie específica alta (@ 1000 m2/g). Se seleccionaron las moléculas que cumplen con el modelo de adsorción de D-R y también se tomaron en cuenta los datos obtenidos con el modelo de D-A, en las cercanías de n = 2 o exactamente 2. Las moléculas seleccionadas conforman el ¨conjunto de entrenamiento¨ (tabla 1) para la obtención del modelo correspondiente. Las moléculas seleccionadas fueron sometidas a la optimización de sus estructuras, mediante los siguientes procedimientos: Mecánica molecular de campos de fuerza (MM+), como primera aproximación., Método semiempírico PM3 (método-3 paramétrico) para garantizar la estructura óptima de la molécula, ambas incluidas en el programa Hyperchem, versión 6.03, habiéndose elegido un gradiente de 0.01 kcal/Å para la optimización de la geometría. Se calcularon las energías HOMO, LUMO de cada una de las moléculas seleccionadas para su incorporación en el conjunto de descriptores. Se calcularon descriptores para cada una de las moléculas seleccionadas, mediante el programa DRAGON, versión 5 disponible en la página web [19] a los que fueron añadidos los descriptores HOMO, LUMO calculados y la diferencia entre los dos niveles de energía. Con todos los descriptores calculados se forma una matriz total de 815 descriptores por 36 moléculas, incluida la constante igual a 1.
EXPERIMENTAL
Se realizó el proceso de adsorción de etileno C2H4 sobre 3 muestras de carbón activado granulado (CAT, Shirasagi, CG900) y 2 muestras de carbón activado en polvo (Norit y Fluka) en un equipo volumétrico de adsorción de gases. El proceso de limpieza se llevó a cabo por una combinación de evacuación y calentamiento, en un equipo construido para el efecto; mismo que utiliza un sistema de vacío que consta de una bomba difusora de mercurio asistida por una bomba mecánica de aceite, Trivac Leybold Heraus tipo D4A.
Tratamiento estadístico-obtención del modelo matemático
Básicamente, los métodos QSAR y QSPR, son relaciones matemáticas arbitrarias y se puede representar mediante la ecuación (10-5):
P = f (D1, D2, D3, ..., Dn) (3)
Donde: P es la propiedad o la actividad a ser aproximada (parámetro k), f es una función matemática arbitrariamente escogida que en el presente caso es una función lineal y D1, D2, D3,....Dn, son los descriptores, ya sean topológicos, electrónicos, mixtos ó simplemente propiedades, para los cuales se requiere que sean independientes entre ellos con el objeto de evitar descripciones sobreabundantes.
El tratamiento estadístico consiste en realizar los cálculos de regresión lineal de cada uno de los conjuntos de descriptores (d), escogido de un número mayor de descriptores (D), con el criterio de elegir aquel conjunto de descriptores d con la desviación estándar (Stot) más pequeña [20,21]. Para llevar a cabo esta selección existen varios métodos. Uno de ellos es el método de búsqueda completa (FS) que requiere D!¤ [(D-d)!d!] regresiones lineales, que evidentemente es un número demasiado grande a medida que D aumenta, haciendo que el método de búsqueda sea computacionalmente muy costoso. Sin embargo, si D es más pequeño que el número de moléculas M, entonces, se puede esperar un conjunto óptimo global de descriptores y la comparación de los mejores descriptores de d = 1, 2, 3, .., D requiere un total de 2D-1 regresiones lineales [22].
El método de reemplazo propuesto por Duchowicks et al [22] permite obtener un conjunto de descriptores d cercanos al óptimo con un número de regresiones lineales que es mucho más pequeña que la requerida por el método de búsqueda total. En lugar de remover variables, este procedimiento consiste en reemplazar una variable seleccionada de un conjunto por otro que minimice la Stot. El método elige d descriptores {X1,X2, ..Xd} aleatoriamente y realiza regresiones lineales. Se elige uno de los descriptores de este conjunto, por ejemplo, X1 y se reemplaza éste por cada uno de los descriptores de la gran cantidad que componen el conjunto D (excepto él mismo) guardando el mejor conjunto resultante. Uno puede empezar reemplazando cualquiera de los d descriptores en el modelo inicial, por lo cual una ecuación de regresión con d variables
tiene d caminos posibles para alcanzar el resultado final. Luego, se elige la variable con el error relativo más grande en su coeficiente (excepto del que fue reemplazado en el paso previo) y reemplaza éste con todos los demás descriptores (excepto él mismo) guardando otra vez el mejor conjunto. Reemplaza todas las variables que quedan de la misma manera como fue hecha en los anteriores pasos y cuando termina, empieza otra vez con la variable que tiene el error relativo más grande en los coeficientes y repite todo el proceso. El proceso se lleva a cabo cuantas veces sea necesario hasta que el conjunto de descriptores permanezca inalterable. Al final, se tiene el mejor modelo para el camino i. Se procede de la misma manera para todos los caminos posibles, i = 1, 2, ..d, se comparan los modelos resultantes y se guarda el mejor. El método tiene un aditamento especial, el cual consiste en realizar la inter-correlación entre los descriptores del modelo determinado.
Validación del modelo
A falta de más datos experimentales, la validación del modelo se realizó mediante el método de validación cruzada ¨leave one out¨, la que consiste en eliminar una molécula de las N moléculas del conjunto de entrenamiento y obtener el modelo con las N-1 moléculas, para luego aplicarla y predecir la propiedad de la molécula que se omitió. Este procedimiento se repite con la segunda, la tercera, cuarta, etc. molécula hasta completar con las N moléculas, de modo que se obtendrán las propiedades predichas para todas ellas. Cada evento se realiza con la reposición de la molécula previamente extraída.
Para que el modelo tenga mayor poder de predicción, se realizó la validación ¨leave more out¨, una técnica muy parecida a la validación leave one out, que consiste en eliminar una cantidad n de moléculas y con las restantes N-n moléculas se construye el modelo y luego éste se aplica para predecir las propiedades de las moléculas extraídas. Esto se hace con todas las moléculas del conjunto de entrenamiento y con reposición de las moléculas previamente extraídas. Para el presente caso, se eliminaron de a 4 moléculas, que corresponde a aproximadamente el 10% de leave more out de las moléculas del conjunto de entrenamiento.
El mejor modelo
Es importante elegir el mejor modelo para su aplicación en la predicción del
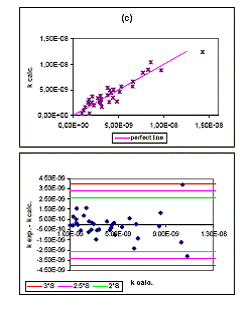
Fig 1. Resultados obtenidos para el modelo de 4 descriptores
parámetro k. Para ello se han obtenido 6 modelos matemáticos de 1, 2, 3, 4, 5 y 6 descriptores. El modelo de 4 descriptores presentó un mayor valor de R deducido de un gráfico de coeficientes de correlación encontrados en función al número de descriptores d, además, se observó que a mayor número de descriptores la curva alcanzaba una asíntota que se acercaba mucho más al valor de 1. Sin embargo, por cuestiones prácticas fue necesario tomar en cuenta algunos aspectos a fin de decidir el modelo óptimo. Así, por ejemplo, la relación número de moléculas/número de descriptores (N/d) no debe ser menor a 5 (el límite generalmente aceptado [23]).
Considerando lo dicho anteriormente, se realizaron las pruebas con los modelos de 4, 5 y 6 descriptores. El modelo de 6 d mostró excelentes bondades a la hora de predecir. Sin embargo, su universo de aplicación se limitó a un número menor de moléculas, por ser muy rígido a la hora de su aplicación. El modelo de 5 es similar a 6 por el mismo hecho de ser muy drástico en su proyección. El modelo de 4 (ecuación 4) resultó ser el óptimo debido a que su universo de aplicación es válido para un número mayor de moléculas, y además la relación de N/d igual a [24] .
![]()
(4)
Donde: X1 es el descriptor TIC0, X2 es el descriptor AMW, X3 es el descriptor (Ms) y X4 es el descriptor S3K, los números entre paréntesis son los errores relativos de cada coeficiente y k es el parámetro de D-R ya conocido.
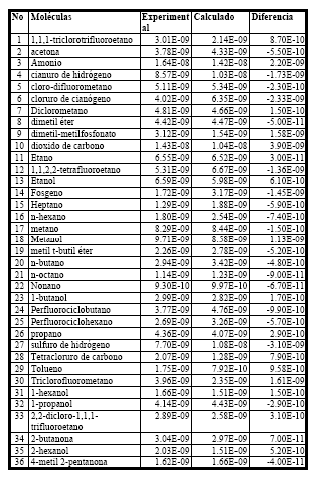
El modelo de 4 d elegido no presenta moléculas "outliers" (molécula eliminada por tener un comportamiento estadístico anómalo), tal como se aprecia en la figura (1b). Es decir, moléculas que tengan una desviación estándar superior a 3S. Existe una buena correlación entre los datos experimentales y los calculados (R=0.90), tal como se ve en la figura (1.a). La tabla 2 muestra los valores de k experimentales y calculados con el modelo de 4 obtenido.
Tabla 2. Valores de k experimental y de calibrado del conjunto de entrenamiento.
Predicción de valores de la constante k
Con el modelo óptimo encontrado (ecuación 4) se hizo la predicción de valores del parámetro k para todas las moléculas de la tabla 3.
Tabla 3.Valores de k predichos para 42moléculas.
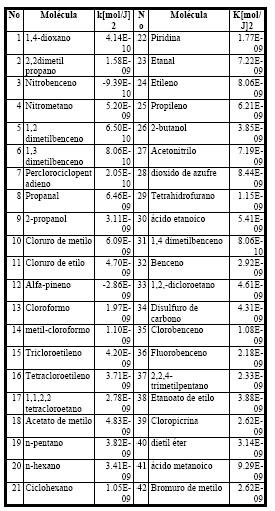
Del conjunto de las 42 moléculas con valores de k predichos, existen dos que tienen valores negativos del parámetro. Esto ocurre debido a que alfa-pineno es una molécula muy grande y la molécula de nitrobenceno es aromática y como en el conjunto de entrenamiento no se tomaron en cuenta este tipo de moléculas, al predecirlos, estos dan valores negativos que no tienen significado físico alguno. Por lo tanto, a estas moléculas no se las toma en cuenta.
Predicción de Capacidades de Adsorción
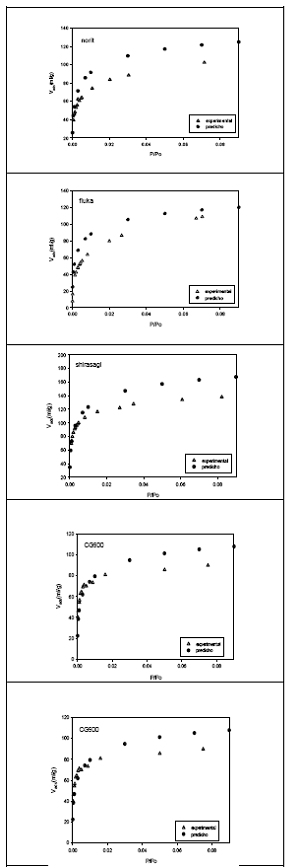
Figura 2. Isotermas de adsorción experimental y predicho de la adsorción de C2H4 a 189.2 K sobre 5 carbones activados
Se ha realizado la predicción de capacidades de adsorción de C2H4 sobre las cinco muestras de carbón activado consideradas en el presente trabajo, principalmente, en el rango representativo (rango donde se producen cambios importantes de cantidades adsorbidas) de presiones relativas de 10- 3 a 0.05. Para el cálculo de las capacidades de adsorción se emplearon los valores de volúmenes de microporos de la tabla 1.
Tal como se puede apreciar en los gráficos, las isotermas de adsorción experimental y predicho, a muy bajas presiones, se comportan de una manera muy similar hasta un punto cercano al máximo de adsorción a partir de la cual las ramas de las isotermas se separan. La isoterma de adsorción de etileno sobre carbón activado CAT parece reproducirse mucho mejor que los otros, debido quizá a que éste, posee características similares al carbón activado BPL. Norit y fluka tienen las isotermas más separadas por ser materiales que tienen partículas muy finas y que presentan características de carbones activados con presencia de mesoporos.
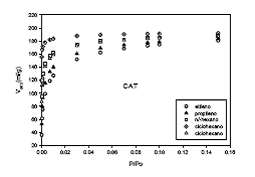
Figura 3. Isotermas de adsorción de vapores predichas sobre carbón activado CAT a la temperatura de 189.2 K.
Otra de las causas para que no haya una buena reproducción de las isotermas de adsorción experimentales, se debe a que el modelo de 4 descriptores es de carácter muy general, es decir, trata de abarcar la mayor cantidad de moléculas en desmedro de la exactitud en la predicción.
También se pueden determinar capacidades de adsorción en función de la temperatura y en el presente trabajo se ha elegido la muestra CAT como la más representativa para mostrar cómo varían las isotermas de adsorción de etileno en función de la temperatura (figura 4). De la misma manera se pueden representar isotermas de las otras moléculas para las cuales se ha predicho el parámetro k.
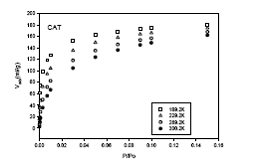
Figura 4. Isotermas de adsorción de etileno sobre carbón activado CAT,
a distintas temperaturas.
Como una manera válida para ejemplificar el alcance del modelo predictivo, se ha calculado las isotermas de varios vapores sobre la muestra de carbón activado CAT (figura 10.6). De la misma manera se puede calcular las isotermas de los otros gases y tomar decisiones que el caso aconseje, como por ejemplo, su aplicación en la descontaminación del aire.
Conclusiones
A partir de la estimación del parámetro k, mediante el modelo matemático obtenido, se pueden predecir las capacidades de adsorción de cualquier vapor de sustancias puras de la tabla 10.3, considerando el tipo de moléculas tomadas en cuenta en el conjunto de entrenamiento (tabla 10.1), sobre carbones activados microporosos, cuya distribución de tamaño de poros o volumen de microporos es conocida, bajo cualquier condición de temperatura (debajo de la temperatura crítica) y a cualquier presión en el rango de bajas presiones relativas, mediante la aplicación de la ecuación de D-R (ecuación 10-4).
Se ha encontrado una metodología para la obtención de modelos de predicción de capacidades de adsorción de carbones activados con pocos datos, sin la necesidad de contar con un conjunto de validación.
Referencias
-
Mihalić Z., Trinajstić, Journal of Chemical Education, 69(9) (1992) 701-712.
-
Duchowiks P, Castro E., Fernandez M. Pre-print.
-
Castañeta H., Castro E., Revista Boliviana de Química, No.1 (2004)
-
Brasquet, C. Bourges, B., Cloirec, P.L.E., Environ. Sci. Techonol., 33(1999) 4228-4231.
-
Berger, B.M., Müller M., Eing, A., Pest. Mang. Sci., 57(2001) 1043-1054.
-
Gerstl, Z., Israel J. Chem., 42(2002) 55-65.
-
Müller, M., Kördel, W, Chemosphere, 32 (12)(1996) 2493-2501.
-
Dearden, J.C., J. Brazilian Chem. Soc., 13(6)(2002) 754-762.
-
Sabljić, A, Güsten, H., Verhaar, H., Hermens J., Chemosphere, 31(11,12) (1995) 4489-4514.
-
Wei, D.B., Wu, C.D., Wang, L.S., Hu, H.Y., SAR/QSAR Environ. Res., 14(3)(2003) 191-198.
-
Urano K., Omori s., Yamamoto E., Environ Science Technology, 16(1982) 10-14.
-
Nirmalakhandan N.N. and Speece R.E.; Environ Science Technology, 27 (1993) 1512-1516.
-
Prakash J., Nirmalakhandan N. and Speece R.E., Env. Sci. Technol. 28(1994) 1403-1409.
-
Qi S., Hay K.J., Rood M.J., and Cal M.P., Journal of Environmental Engineering, 126(2000) 865-868.
-
Dobruskin V.Kh., Carbon 40(2002) 1003-1010.
-
Wu, J., Strömqvist, M.E., Claesson, O., Fangmark, I.E., Hammarströn, L.G., Carbon, 40(14)(2002) 2587-2596.
-
Wu, J., Hammarström, L-G, Claesson, O., Fangmark, I., Carbón, 41(6)(2003) 1322-1325.
-
17. Fängmark, I.E., Hammarström, L-G, Strömqvist, M.E., Ness, A. L., Norman, P.R., Osmond, N.M., Carbon 40(2002) 2861-2869.
-
/www.talete.mi.it/dragon.htm.
-
Lucic B., Nikolic S., Trinajstic N., Juretic D., J. Chem, Inf. Comput. Sci., 35(1995)532-538.
-
Lucic B., Trinajstic N., J. Chem, Inf. Comput. Sci., 39(1999) 121-132.
-
Duchowicz P.R, Castro E.A., Fernández F.M., Alternative Algorithm for the Search of an Optimal Set of Descriptors in QSAR-QSPR theories, IN PRESS, 2005.
-
Tropsha A., Gramatica P., Gombar V.K., QSAR Comb. Sci. 22,(2003), 69-77.
-
Pablo R. Duchowicz_, H. Castañeta, E. A. Castro, F. M. Fernández, J. L. Vicente Atmospheric Environment 40 (2006) 2929–2934.












 uBio
uBio