INTRODUCCIÓN
El desarrollo de competencias matemáticas es crucial porque permite a los estudiantes formular, estructurar y resolver problemas en diversos contextos, desarrollar modelos matemáticos y comunicar soluciones de manera efectiva. Se definen como la habilidad de emplear números, símbolos y operaciones básicas, aplicando el razonamiento matemático para interpretar información e impulsar el conocimiento cuantitativo y espacial de la realidad. Estas competencias fomentan el pensamiento crítico, el razonamiento lógico y la toma de decisiones basadas en análisis cuantitativo, habilidades esenciales en la vida diaria y en el ámbito profesional. Además, el desarrollo de la creatividad, la perseverancia y la capacidad de argumentación mejoran el comportamiento, las habilidades sociales, la motivación y la autoestima de los estudiantes (Sánchez, 2023).
En el bachillerato, el enfoque por competencias pretende que los estudiantes aprendan a pensar matemáticamente, aplicando diferentes soluciones plausibles ante cualquier situación o toma de decisión. Esto les permite construir modelos económicos y sociales, así como integrarse a las demandas presentes y futuras, facilitando la transición del pensamiento concreto al abstracto, permitiendo a los estudiantes desarrollar modelos matemáticos para resolver problemas complejos, fomenta la creatividad, el pensamiento lógico y crítico, permitiéndoles argumentar y estructurar mejor sus ideas y razonamientos (Blanco y Franco, 2021).
En la enseñanza de matemáticas, las estrategias didácticas van más allá de la simple instrucción numérica, fomentando el pensamiento crítico, la resolución de problemas y el razonamiento lógico. Estrategias de gestión, control, procesamiento, apoyo y personalización facilitan la conexión entre conceptos matemáticos y experiencias reales, fortaleciendo la comprensión y la aplicabilidad del conocimiento. Adicionalmente, el uso de estrategias de enseñanza-aprendizaje innovadoras, apoyadas en tecnologías, contribuye significativamente al desarrollo de competencias matemáticas en estudiantes de bachillerato (Moncayo et al., 2024).
Sin embargo, en la actualidad se detectan limitaciones, entre ellas, la insuficiente formación de los docentes en estrategias didácticas para el desarrollo apropiado del proceso de enseñanza y aprendizaje de las matemáticas. Se requiere cambiar el paradigma de que el conocimiento matemático es inalcanzable y favorecer la idea de que este conocimiento es universal, no importando género, etnia, condición social y rendimiento académico. La falta de recursos tecnológicos y la integración herramientas adaptativas y dinámicas que permitan abordar las necesidades individuales de los estudiantes, promoviendo un entorno propicio para la comprensión y aplicación de conceptos matemáticos, son algunos de los elementos que requieren análisis y la toma de decisiones institucionales (Pérez et al., 2021).
En este contexto, se requiere considerar ¿cuáles son las principales dificultades que enfrentan los estudiantes de bachillerato para comprender y aplicar los contenidos matemáticos en su proceso de aprendizaje?, ¿qué estrategias de enseñanza y recursos didácticos pueden ser más efectivos para superar las dificultades en la resolución de problemas matemáticos que experimentan los estudiantes de bachillerato? De ahí que el objetivo del presente artículo de revisión sistemática fue analizar el estado actual de las investigaciones relacionadas con el uso de estrategias de enseñanza y recursos didácticos orientados a superar las dificultades cognitivas y conceptuales que afectan el desarrollo de las competencias matemáticas en estudiantes de bachillerato.
MÉTODO
En el estudio se llevó a cabo una revisión sistemática cualitativa de la literatura con el objetivo de integrar y analizar diferentes investigaciones cuantitativas y cualitativas que abordaron, de manera detallada y crítica, las principales dificultades cognitivas y conceptuales que enfrentan los estudiantes de bachillerato para comprender y aplicar los contenidos matemáticos en su proceso de aprendizaje y las estrategias de enseñanza y recursos didácticos que pueden ser más efectivos para superar estas dificultades en la resolución de problemas matemáticos. A través de un análisis de contenido, se logró resumir la información extraída de los artículos científicos, lo que facilitó una evaluación crítica de los resultados.
Criterios de selección y bases de datos utilizadas
Para sistematizar la información, se seleccionaron artículos publicados entre 2017 y 2025. Se empleó la guía actualizada para la publicación de revisiones sistemáticas PRISMA, siguiendo las etapas de identificación, cribado, elegibilidad e inclusión, lo que facilitó estructurar el proceso. Se efectuó una búsqueda de artículos publicados en español e inglés; en las bases de datos: Scopus, Web of Science, y SciELO.
El análisis de las bases de datos revela que la mayoría de los artículos seleccionados provienen de Scopus, representando el 65% del total, como fuente predominante y confiable en la investigación abordada. Por otro lado, Web of Science y Scielo contribuyen con el 20% y el 15%, respectivamente, lo que indica una diversidad en los estudios consultados, aunque en menor medida. Estas bases de datos se seleccionaron por su relevancia en la investigación académica, Scopus ofrece una amplia cobertura de literatura científica, facilitando el acceso a artículos de diversas disciplinas; el Web of Science permite realizar análisis de citas, enriqueciendo la evaluación del impacto de la investigación y SciELO se centra en la difusión de investigaciones en América Latina, promoviendo el acceso abierto y la visibilidad de estudios regionales. Juntas, estas plataformas fortalecen el proceso investigativo y académico.
Criterios de inclusión y exclusión
Los criterios de inclusión tuvieron en cuenta que fueran artículos de revistas indexadas en las bases de datos seleccionadas; que constituyeran artículos de investigación o revisiones acordes al tema objeto de estudio, que el contenido y las palabras clave estuvieran relacionadas con las palabras claves definidas, competencias matemáticas, resolución de problemas, estudiantes de bachillerato, estrategias de enseñanza, recursos didácticos, dificultades cognitivas y conceptuales; redactados en español e inglés; publicados en el período de 2017 a 2025, de acceso abierto. Se excluyeron aquellos que no cumplían con los criterios de inclusión establecidos y que el nivel de aplicación estuviera en el nivel de enseñanza universitaria o superior.
Estrategias de búsqueda y proceso de selección de estudios
La estrategia de búsqueda se fundamentó en la elección de descriptores apropiados en español, combinando operadores lógicos "Y", "AND", “O” y “OR”. Se aplicaron filtros para limitar la búsqueda a los años comprendidos entre 2017 y 2025.
Perfil 1: "competencias matemáticas" Y "resolución de problemas" Y "estudiantes de bachillerato"
"mathematical skills" and "problem solving" in "high school students"
Perfil 2: "estrategias de enseñanza" Y "recursos didácticos" Y ("dificultades cognitivas" O "dificultades conceptuales")
"teaching strategies" AND "teaching resources" AND ("cognitive difficulties" OR "conceptual difficulties")
Perfil 3: ("competencias matemáticas" O "resolución de problemas") Y "estudiantes de bachillerato"
("mathematical skills" OR "problem solving") AND "high school students"
Perfil 4: "estrategias de enseñanza" Y ("competencias matemáticas" O "recursos didácticos") Y "dificultades cognitivas"
"teaching strategies" AND ("mathematical skills" OR "teaching resources") AND "cognitive difficulties"
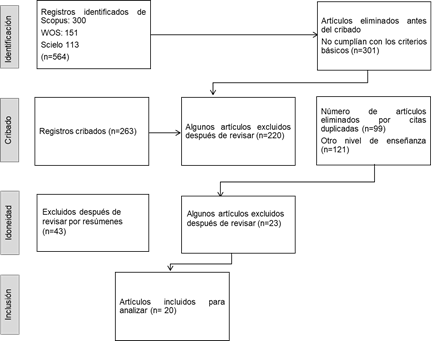
La búsqueda fue trabajada independientemente por cada autor, consolidándose en el proceso de análisis y registro de los artículos. La guía PRISMA permitió presentar de manera estructurada y transparente, la evaluación clara de los hallazgos, la calidad de los estudios incluidos y la certeza de las evidencias obtenidas a partir de las revisiones sistemáticas. De los 564 artículos iniciales, En la etapa de identificación se eliminaron 301 que no cumplían con los criterios básicos; en la fase de cribado se eliminaron 220, de ellos 99 por duplicado y 121 por estar relacionados con el nivel de educación superior, resultando en 43 estudios pertinentes; en la fase de idoneidad se revisaron títulos y resúmenes, excluyendo 23, luego de una revisión más detallada se incluyeron 20 estudios que cumplieron con todos los criterios establecidos Figura 1.
Una vez seleccionados los artículos, se procedió a analizar su contenido. Se elaboraron matrices que incluyeron elementos necesarios para determinar el impacto que las metodologías usadas tuvieron en el desarrollo de las competencias matemáticas de los estudiantes de bachillerato.
DESARROLLO Y DISCUSIÓN
La revisión sistemática de la literatura científica, realizada entre los años 2017 y 2025, permitió identificar y analizar las investigaciones más relevantes y recientes en este ámbito. En la tabla 1 se muestra que de los 20 trabajos revisados el 50% provienen de América Latina, representados por México, Perú, Colombia, Chile y Ecuador, reflejando un interés regional por mejorar la enseñanza de las matemáticas. Europa aporta un 17%, con investigaciones de España, Grecia, Bélgica, Italia; mientras que Asia y Norteamérica contribuyen con un 11% cada uno, desarrollados por Indonesia y Estados Unidos. Esta distribución evidencia un enfoque global en la investigación educativa, destacando la relevancia de América Latina como región clave para abordar desafíos en competencias matemáticas y estrategias pedagógicas.
En los estudios se destacan el uso de estrategias innovadoras como la realidad aumentada y ambientes de aprendizaje socioculturales propuestos por Ramírez (2017), que fomenta el razonamiento lógico y la resolución de problemas al conectar conceptos abstractos con aplicaciones prácticas. Por su parte, Alvis et al. (2019), subrayan que integrar las matemáticas en contextos sociales permite a los estudiantes reflexionar sobre problemas cotidianos, promoviendo una ciudadanía crítica.
Estudios como el de Flores y Juárez (2017), demostraron que el aprendizaje basado en proyectos mejora el pensamiento crítico y creativo al conectar problemáticas locales con soluciones matemáticas. Amador et al. (2021), por su parte, implementaron un curso propedéutico que redujo significativamente las deficiencias matemáticas de estudiantes de nuevo ingreso a nivel universitario. Finalmente, Backhoff et al. (2022), validaron el uso del Modelo de Crédito Parcial para evaluar competencias matemáticas con precisión.
Se destacan cuatro estudios de Perú que presentan estrategias como el aprendizaje activo y la gamificación, como metodologías que mejoran significativamente las competencias matemáticas en comunidades indígenas e incrementan la motivación estudiantil mediante experiencias dinámicas e interactivas (Chávez et al., 2021; Gutierrez y Meleán, 2023; Rosales et al., 2023; Cueva, 2023). En esta línea son los aportes de Forrester y Covington (2023), quienes desarrollaron actividades culturalmente receptivas para abordar las dificultades derivadas de la diversidad étnica, combinando prácticas participativas con actividades basadas en la comunidad para fortalecer tanto las competencias matemáticas como las identidades culturales de los estudiantes.
Ríos y Navarrete (2023) y Valenzuela et al. (2024) hallaron que Moodle mejora la comprensión matemática y se adapta a los ritmos individuales. García y Martín (2023) lograron mejoras en competencias digitales y matemáticas usando GeoGebra. Moreno et al. (2023) integraron sostenibilidad con proyectos colaborativos, fomentando actitudes críticas. Rahmawati et al. (2024) diseñaron un modelo instruccional que integra pensamiento computacional y matemático, preparando a alumnos para el futuro.
Tabla 1 Síntesis del uso e impacto de las estrategias de enseñanza y recursos didácticos en la enseñanza de las matemáticas.
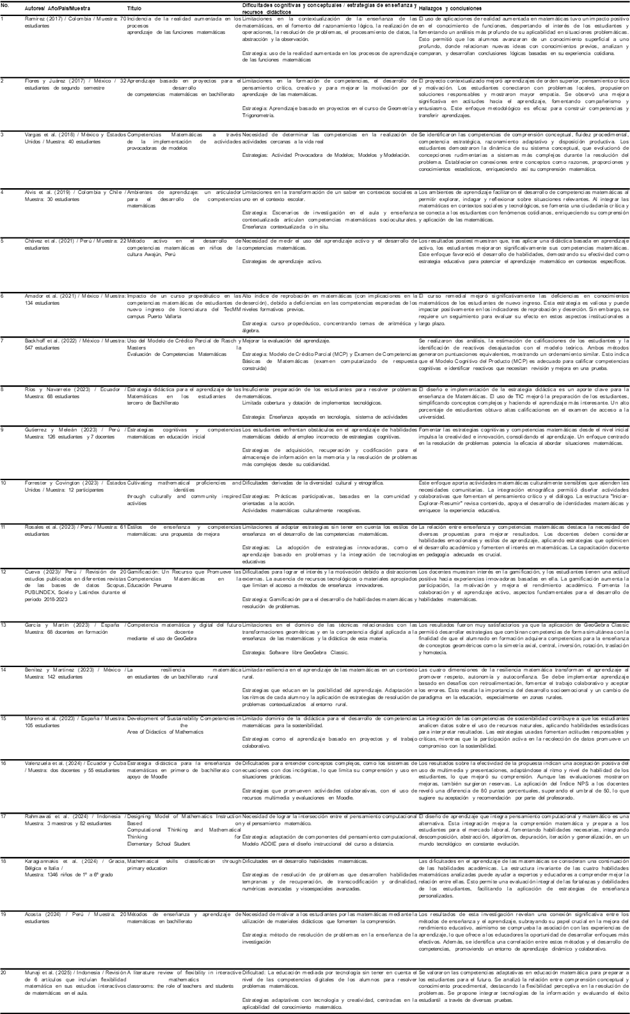
Los estudios analizados implementaron diversas estrategias pedagógicas que comparten elementos clave, a) el aprendizaje activo, como demuestran Chávez et al. (2021) y Cueva (2023), que aumenta la motivación al involucrar a los estudiantes en su proceso educativo; b) la contextualización, fundamental, como indica Alvis et al. (2019), al integrar las matemáticas en problemas sociales relevantes para fomentar una ciudadanía crítica; c) el uso de tecnología, evidenciado por García y Martín (2023) y Valenzuela et al. (2024), facilita la comprensión de conceptos complejos y mejora la participación estudiantil; d) la gamificación, según Cueva (2023), no solo mejora el rendimiento académico, sino que también fomenta la colaboración entre estudiantes y e) un enfoque culturalmente receptivo, propuesto por Forrester y Covington (2023), resaltan la importancia de adaptar actividades a contextos culturales específicos para fortalecer competencias académicas e identidades personales.
Los resultados generales reflejan avances significativos en el desarrollo de competencias matemáticas:
Las estrategias activas promueven habilidades críticas como razonamiento lógico, resolución de problemas e innovación.
La tecnología educativa facilita el aprendizaje adaptado a diferentes niveles.
La contextualización conecta conceptos abstractos con aplicaciones prácticas.
La gamificación incrementa la motivación estudiantil.
Los enfoques culturalmente receptivos abordan desafíos derivados de la diversidad étnica.
Sin embargo, también se identificaron limitaciones comunes, como la falta de recursos tecnológicos adecuados en algunos contextos, la necesidad de capacitar a docentes para implementar metodologías innovadoras y el requerimiento de seguimiento longitudinal para evaluar impactos a largo plazo.
Los hallazgos subrayan la importancia de continuar explorando metodologías pedagógicas efectivas que no solo mejoren el rendimiento académico sino también fomenten habilidades críticas necesarias para enfrentar desafíos globales actuales y futuros.
Discusión
Las dificultades encontradas en la enseñanza-aprendizaje de las matemáticas y las estrategias adoptadas en los estudios analizados se alinean con diversas investigaciones que destacan su impacto positivo en este proceso.
Un aspecto recurrente es la falta de estrategias cognitivas adecuadas, lo que se traduce en problemas para resolver problemas matemáticos y comprender conceptos fundamentales, este aspecto coincide con Valverde y Díaz (2021), quienes analizan que estas dificultades pueden surgir desde etapas tempranas, afectando la capacidad de los estudiantes para desarrollar habilidades necesarias en niveles más avanzados. Por su parte, Jiménez et al. (2024), consideran que la implementación efectiva de estrategias metacognitivas se pueden convertir en una herramienta fundamental para el desarrollo del pensamiento crítico en los estudiantes.
La variabilidad en los estilos de aprendizaje es otro factor crítico mencionado en los estudios, coincidiendo con Sarango et al. (2024), quienes destacan que esto puede diferir considerablemente entre los estudiantes. La falta de adaptación de las estrategias pedagógicas a estos estilos puede generar incomodidad y confusión, lo que resulta en mayores dificultades para comprender y aplicar los contenidos. En este sentido, la personalización del aprendizaje se vuelve esencial para abordar las necesidades individuales de cada estudiante, facilitando así un entorno más inclusivo y efectivo.
Además, la carencia de recursos adecuados para la enseñanza de las matemáticas desempeña un papel clave en el aprendizaje, la falta de materiales didácticos y enfoques innovadores contribuye directamente a las dificultades que enfrentan los estudiantes. En este aspecto, se concuerda con Jimenez et al. (2024), quienes proponen la implementación de métodos como el aprendizaje basado en problemas como solución viable, ya que este enfoque promueve una comprensión activa y práctica de los conceptos matemáticos, permitiendo a los estudiantes aplicar lo aprendido a situaciones reales.
Los resultados del análisis de los estudios, permite concordar con Meza et al. (2024), cuando plantean que la ansiedad o el rechazo hacia las matemáticas también son factores que obstaculizan la motivación y disposición para aprender, ya que pueden sentirse abrumados por la complejidad de los conceptos matemáticos. La retroalimentación continua y específica es otra estrategia clave identificada en diversos estudios, ya que permite a los estudiantes comprender sus errores y aprender de ellos.
El uso de herramientas tecnológicas y simulaciones interactivas ha demostrado ser efectivo en la enseñanza de matemáticas, en este aspecto coinciden Chica et al. (2024), quienes consideran que estas herramientas facilitan la comprensión de conceptos abstractos y hacen el aprendizaje más atractivo para los estudiantes. Realizan una propuesta de procedimientos metodológicos que reflejan una secuencia que garantiza al docente la posibilidad de desarrollar sus clases con el uso de la realidad aumentada, como herramientas que forman parte del trabajo colaborativo, como otra estrategia que favorece el aprendizaje; trabajar en grupos permite a los estudiantes compartir diferentes enfoques y resolver problemas juntos, enriqueciendo así su comprensión del material6.
Los autores contrastados, confirman que las dificultades que enfrentan los estudiantes de bachillerato al aprender matemáticas son multifacéticas e interrelacionadas. Desde la falta de estrategias cognitivas adecuadas hasta la carencia de recursos didácticos y el impacto del entorno escolar, todos estos factores contribuyen a un panorama complejo que requiere atención y soluciones innovadoras. Implementar enfoques pedagógicos adaptativos como el aprendizaje basado en proyectos, junto con el uso efectivo de tecnología y colaboración entre estudiantes, puede ser clave para mejorar el aprendizaje en esta área crítica.
CONCLUSIONES
El análisis de los estudios seleccionados destaca la diversidad de estrategias pedagógicas para desarrollar competencias matemáticas en estudiantes de bachillerato, el aprendizaje activo es fundamental, incrementando la motivación al involucrar a los estudiantes en su proceso educativo; la contextualización integra las matemáticas en problemas sociales relevantes, fomentando una ciudadanía crítica; la tecnología facilita la comprensión de conceptos complejos y mejora la participación; la gamificación optimiza el rendimiento académico y fomenta la colaboración; mientras que un enfoque culturalmente receptivo adapta actividades a contextos específicos, fortaleciendo competencias e identidades personales.
Se delimitan las deficiencias en el proceso de desarrollo de competencias matemáticas como la falta de recursos, la necesidad de capacitación docente y el seguimiento a largo plazo. Estos hallazgos subrayan la importancia de continuar explorando metodologías pedagógicas efectivas que mejoren el rendimiento académico y fomenten habilidades críticas necesarias para enfrentar los desafíos globales actuales y futuros, en particular, la integración de la realidad aumentada como una herramienta prometedora para enriquecer la enseñanza de matemáticas, aunque su implementación exitosa requiere abordar barreras como la capacitación docente y la disponibilidad de recursos tecnológicos
La combinación del pensamiento computacional con el matemático prepara a los alumnos para desafíos laborales futuros, mejorando su comprensión conceptual mediante procesos como la descomposición y los algoritmos. La diversidad étnica también debe ser abordada con actividades culturalmente receptivas que combinen prácticas participativas con actividades basadas en la comunidad para fortalecer tanto las competencias matemáticas como las identidades culturales de los estudiantes.