INTRODUCCIÓN

A nivel internacional, el informe "Digital 2020" de Hootsuite y We Are Social revela que 4.538 millones de personas en el mundo son usuarias de Internet, lo que representa un aumento del 7% respecto al año anterior, equivalente a 298 millones de nuevos usuarios. Además, estos usuarios pasan en promedio 6 horas y 43 minutos conectados al día, lo que equivale a más de 100 días al año, y en el 92% de los casos acceden a Internet a través de un teléfono móvil. En el contexto de los adolescentes, el uso de Internet se centra principalmente en el entretenimiento (Álvarez y Muñoz, 2019). Sin embargo, en los niveles de educación básica y universitaria, el propósito de la búsqueda de información está predominantemente orientado a necesidades académicas.

Según ^{Alcibar et al., (2018}), el uso de computadoras e Internet de manera interactiva y divertida influye positivamente en el aprendizaje. En cuanto al acceso y uso, se observa que el 74,7% de los jóvenes universitarios reconoce llevar más de cinco años utilizando Internet, lo que significa que siete de cada diez han estado navegando en la red durante varios años (^{Morales et al., 2020}). Este cambio ha provocado que la tecnología reemplazara, en gran medida, procesos mentales previos, como los cálculos matemáticos, las inferencias, las deducciones y las probabilidades, los cuales eran esenciales en el desarrollo del pensamiento matemático.

Los estudiantes aplican conceptos lógico-matemáticos en su día a día a través de diversas experiencias educativas, lo que convierte al pensamiento matemático en una herramienta clave en su proceso de aprendizaje. En este ecosistema educativo, tanto la familia como los docentes juegan roles fundamentales, ya que deben colaborar para identificar y aplicar prácticas pedagógicas efectivas que faciliten a los estudiantes la comprensión y el sentido de su entorno (^{Aroca y Cauty, 2017}).

Por lo tanto, el proceso de construcción del conocimiento de un alumno requiere establecer conexiones significativas con situaciones y objetos, lo que le permite desarrollar un pensamiento lógico mediante la clasificación de las relaciones simples entre los objetos previamente establecidos. Estos conocimientos y habilidades resultan ser de gran valor para el ser humano, ya que, además de la habilidad de contar, el individuo desarrolla su capacidad para razonar y reflexionar sobre cualquier situación de interés (^{Berkowitz y Elsbeth, 2022}). Así, es imperativo que los educadores sean innovadores y adopten estrategias pedagógicas que favorezcan el desarrollo continuo del pensamiento matemático a lo largo de la trayectoria académica de los estudiantes (^{Burgos y Chaverry, 2023}).

En este sentido, es crucial que los educadores cuenten con los conocimientos y habilidades necesarios para diseñar las estrategias más eficaces que promuevan el razonamiento matemático y el pensamiento crítico de los estudiantes en el aula. En el contexto educativo, resulta esencial destacar la importancia de hacer un seguimiento constante del progreso de los alumnos, lo que contribuye a una enseñanza más personalizada y efectiva (^{Charalambous et al., 2022}).

Las universidades nacionales y particulares, tanto en la capital como en el resto del Perú, no están exentas de esta problemática. Muchos de los planes de estudio de las universidades que imparten cursos de matemáticas superiores se basan principalmente en el razonamiento abstracto, priorizando la complejidad sobre la aplicabilidad. Esto lleva a la formación de estudiantes mecanizados, que se enfocan en procedimientos operativos sin una comprensión profunda (^{Cifuentes y Villa, 2017}).

Los estudios neuropsicológicos han aportado nueva información sobre la "arquitectura cognitiva" del procesamiento numérico. La existencia de disociaciones entre la lectura y escritura de números, tanto en notación arábiga como en palabras, y las diferencias entre las operaciones aritméticas, sugiere que cada una de estas habilidades se asocia con redes neuronales altamente especializadas, pero que están interconectadas entre sí (^{Cilli et al., 2023}).

De esta manera, es fundamental garantizar que los estudiantes de pregrado en la especialidad de matemáticas desarrollen de manera óptima su pensamiento matemático. Al lograrlo, estarán mejor preparados para enfrentar desafíos cognitivos, resolver problemas complejos y aplicar principios matemáticos de forma efectiva en diversos contextos académicos y profesionales. La falta de desarrollo del pensamiento matemático puede ocasionar problemas de bajo nivel en la inferencia lógica y dificultades en el planteamiento y resolución de problemas en contextos reales.

Los estudiantes de pregrado en la especialidad de matemáticas presentan un nivel bajo de pensamiento matemático, evidenciado por sus dificultades para argumentar y relacionar procesos, comprender problemas, identificar elementos clave, comparar problemas matemáticos, elaborar conclusiones y atribuir significados matemáticos, emitir juicios y generalizar propiedades, sin una valoración e identificación significativa con la matemática (Sarmiento et al., 2017). Esta deficiencia también afecta el desarrollo de la inteligencia espacial y lógica. En los últimos años, los estudiantes se han vuelto dependientes de dispositivos móviles que cuentan con aplicaciones para resolver ejercicios matemáticos, como Photomath, que permite reconocer patrones matemáticos y mostrar soluciones directamente en la pantalla, lo que reduce el esfuerzo cognitivo necesario para desarrollar habilidades matemáticas profundas.

Si esta problemática no se aborda, la consecuencia principal sería la falta de un análisis exhaustivo y sistemático sobre el desarrollo del pensamiento matemático a través de estrategias hermenéuticas. Esto dificultaría la identificación y comprensión de los factores que influyen en dicho desarrollo, así como la evaluación de la efectividad de estas estrategias en el mejoramiento del pensamiento matemático. Además, la ausencia de una revisión sistemática limitaría la capacidad para sintetizar la evidencia disponible y generar conclusiones basadas en la totalidad de los estudios relevantes.

En este contexto, surge la interrogante: ¿Cuál es el impacto de las estrategias hermenéuticas en el desarrollo del pensamiento matemático, en términos de la comprensión de conceptos matemáticos, los enfoques didácticos para fomentar el crecimiento del razonamiento matemático, y el uso de materiales didácticos y entornos de aula? Por lo tanto, el presente estudio tiene como objetivo analizar el desarrollo del pensamiento matemático mediante estrategias hermenéuticas, con el fin de ofrecer una visión integral de este campo de investigación y sus implicaciones para la práctica educativa.

METODOLOGÍA

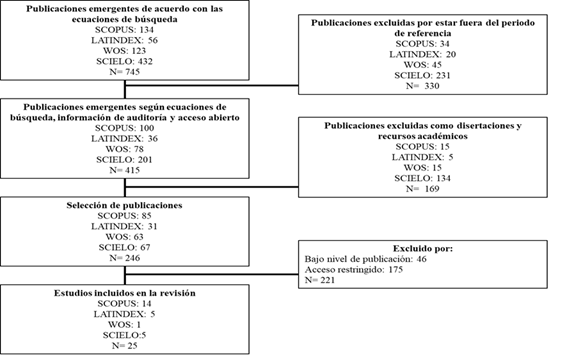
La investigación fue una revisión sistemática, donde se aplicó los lineamientos establecidos dentro de la declaración PRISMA, es por ello que se desarrollan las siguientes fases: a) formulación del objetivo b) definición de las ecuaciones de búsqueda, c) establecimiento de los criterios de inclusión y exclusión, d) diagrama de flujo del proceso de búsqueda y selección, e) revisión de las bibliografías, f) análisis de las fuentes secundarias de información y g) organización y discusión de los resultados (Bayuo, et. al., 2023).

Formulación del objetivo de investigación

El estudio se planteó como objetivo de investigación analizar el desarrollo del pensamiento matemático por medio de estrategias hermenéuticas, con el fin de proporcionar una visión integral de este campo de investigación y sus implicaciones para la práctica educativa.

Procesamiento para la búsqueda de información

Para la indagación de la investigación, se emplearon las base de datos SCOPUS, SCIELO, WOS, entre otros, esto por su relevancia y fácil acceso a los documentos a revisar por los autores, árbitros y lectores, consecuentemente, se fijaron los siguientes criterios de inclusión: 1) artículos publicados desde el 2017 hasta el 2023, 2) artículos de revisión bibliográfica y originales, 3) estudios con palabras clave: “desarrollo del pensamiento matemático”, “estudiantes universitarios”, “estrategias hermenéuticas”. Asimismo, se fijaron los siguientes criterios de exclusión: 1) estudios duplicados, 2) estudios como disertaciones y recursos académicos, 3) estudios con bajo nivel de publicación, 4) estudios con acceso restringido.

Consecuentemente, la búsqueda se realizó luego de la determinación de las palabras clave: “aprendizaje”, “enseñanza”, “estrategias”, “hermenéutica”, “pensamiento matemático”, que propiciaron a la construcción de las ecuaciones de búsqueda, las cuales fueron formuladas combinando entre ellas el término booleano “AND”; y, para no limitar los resultados, se incluyeron descriptores en el constructo internacional, los cuales fueron debidamente traducidos, derivando expresiones como “desarrollo cognitivo” AND “pensamiento matemático” AND “estudiantes universitarios” AND “estrategias hermenéuticas” AND “educación”, identificando estudios que exploraran cada una de las categorías o unidades de análisis por medio de estas palabras claves conciliadas en los títulos de las investigaciones, resúmenes y desarrollo temático.

Recolección y examen de la información

Se revisó y seleccionó la bibliografía sistemáticamente, atendiendo a: a) fecha de publicación, b) autor, c) título y d) país de origen del levantamiento del estudio. En la figura 1 se detalla el proceso de exclusión de documentos, desechando en primera instancia aquellas investigaciones fuera del período indagatorio, luego las disertaciones, recursos catedráticos, investigaciones de otro alcance y finalmente se excluyeron los artículos con acceso restringido. Consecuentemente, luego de este proceso se seleccionaron 25 artículos que fueron revisados y analizados de forma artesanal por medio del empleo de un emulador de repetición de palabras disponible en: http://www.repetition-detector.com/?p=online, siendo esta una herramienta eficiente para la condensación de las palabras claves suficientes que dan sustento científico a los artículos; y, promoviendo también la idoneidad temática.

Figura 1 Flujograma PRISMA del proceso de sistematización de la información. 

Finalmente, los documentos seleccionados fueron procesados a través de una herramienta de acceso abierto de análisis de contenido, como Estilector, que fue útil para la identificación de las palabras que más se repitieron dentro de los archivos. Además, se elaboró una ficha bibliográfica a modo de sistematización de los datos a revisar.

DESARROLLO Y DISCUSIÓN

A continuación, se procede a presentar los resultados principales relacionados con el desarrollo del pensamiento matemático por medio de estrategias hermenéuticas, sinterizados en la Tabla 1, la cual permite tener una visión más amplia y una estructura lógica de la información.

Tabla 1 Matriz de síntesis. 

Se puede evidenciar que los estudios apuntan al análisis del desarrollo del pensamiento matemático en estudiantes universitarios por medio de estrategias de relevancia como la hermenéutica, se evidencian también estudios que se abordan en Latinoamérica como Colombia; que, marcan hito elemental de complemento al estudio. Asimismo, abordar el conocimiento del desarrollo de estas herramientas dentro del enfoque analítico parte de las diferentes áreas de conocimiento que describen la continuidad del mismo, centrando gran concentración en el marco de la educación en el 100% de los recursos seleccionados para la revisión sistemática.

Publicaciones por países de procedencia

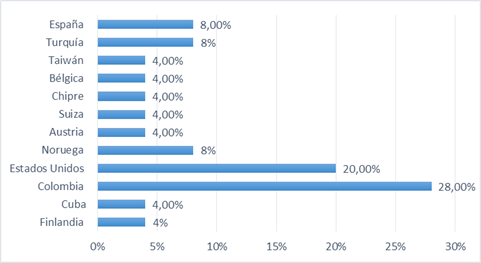
En la Figura 1 se evidencian los estudios organizados por país de producción científica. Aunque la selección de dichas áreas se limita mayoritariamente a países latinos como Colombia y del norte como Estados Unidos, resulta importante mostrar la tendencia de este tipo de investigaciones abordadas dentro del estudio.

Figura 1 Publicaciones por país de procedencia. 

La revisión ha permitido realizar un análisis de los países de relevancia de producción científica dentro de la revisión sistemática de información, se evidencia que el mayor número de publicaciones fue en Colombia representando el 28% (7) de los recursos científicos tomados en consideración para la revisión, por su parte, se evidencia que el 20% (5) de los artículos resultantes del cribado se condensan en Estados Unidos, asimismo, el 8% (2) se concentra en países como España, Turquía y Noruega; finalmente, el 4% (1) se distribuye en países como Taiwán, Bélgica, Chipre, Suiza, Austria, Cuba y Finlandia.

Publicaciones por año

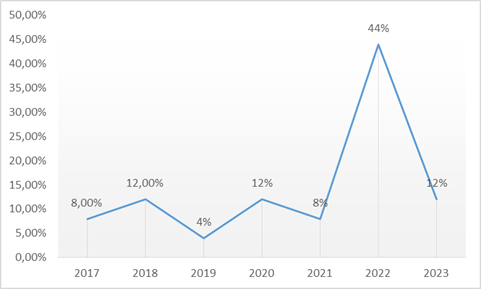
Respecto a la producción anual de los artículos seleccionados para la discusión de la revisión sistemática, se puede apreciar que el año 2022 tuvo mayor prevalencia de producción científica representando el 44% (11) de la muestra de análisis sistemático, asimismo, el 12% (3) de producción se refleja en los años 2023, 2020 y 2018; el 8% (2) de la producción se esclarece en los años 2021 y 2017; y, finalmente, el 4% (1) se evidencia en el año 2019.

Figura 2 Publicaciones por año. 

En este punto es necesario destacar que la información presentada es fluctuante, es decir, el abordaje anual de esta temática depende de la necesidad científica de aportar cimientos relacionados a la temática de estudio. Sin embargo, las tendencias actuales o dentro del período indagatorio de la presente revisión sistemática apuntan al abordaje de los elementos necesarios para llevar a una gestión por resultados en obras públicas y su relación en la calidad de vida del poblador dentro del marco peruano.

Por otro lado, el análisis de los datos condujo al desarrollo de 38 códigos distintos (mostrados en la Figura 3), cada uno de los cuales aborda uno de tres temas emergentes de la revisión sistemática: (a) comprensión de conceptos matemáticos, (b) enfoques didácticos para fomentar el crecimiento del razonamiento matemático, y (c) materiales didácticos y entornos de aula. Estos códigos hacen referencia a todos los procesos intrínsecos relacionados por medio del análisis hermenéutico abordado dentro de los diferentes estudios sistematizados, estos se esclarecen dentro de una nube de palabras informativa que esboza el ambiente, el aprendizaje, la asociación, la clasificación, los componentes, los conocimientos, la construcción, la creatividad, el diagnóstico, la disposición, la diversidad de material, la dotación, las enseñanzas, los espacios, las estrategias, la evaluación, las etapas o fases, la experimentación, la falta de recursos, la formación, la guía de indicadores, el incumplimiento de planificación, la innovación, la instrucción, el interés, los juegos, el análisis matemático, la motivación, los materiales didácticos, las necesidades, la observación, el proceso lógico matemático, la planificación, el poco conocimiento, el potenciar, el proceso, el razonamiento y los recursos.

Figura 3 Nube de palabras de la sistematización de información. 

Comprensión de conceptos matemáticos

Esta dimensión o subtema muestra las creencias predominantes de los profesores sobre el pensamiento matemático, su fundamentación en el currículo de la enseñanza superior, los diversos procesos que intervienen en el pensamiento matemático y el dominio demostrado por los profesores de las técnicas para suscitar la participación de los alumnos en el proceso de razonamiento lógico-deductivo (^{Cronin y Stewart, 2022}; ^{Cilli et al., 2023}).

Según los estudios comentados, se dice que la lógica matemática se compone de las habilidades para clasificar y ordenar objetos, así como factores ambientales y cantidades numéricas (Daz y Dáz, 2018). Otro docente colaborador demuestra que esta forma de pensar es la concepción que tiene el estudiante sobre el espacio, los números y las formas, revelando una posible influencia marcada en la formación terciaria del docente y sus ideas sobre este tema por medio de elementos o herramientas hermenéuticas para distinguir las necesidades de aprendizaje necesarias para establecer puntos de referencia (^{Erkan y Kar, 2022}; ^{Giacomone et al., 2018}).

Como se puede observar dentro de los artículos analizados, las conexiones realizadas entre los distintos códigos revelan que, según las fuentes, el proceso de razonamiento matemático se sitúa en el ámbito del aprendizaje del entorno, que forma parte del currículo de la educación superior (^{Lahdenpera et al., 2022}). Otros estudios expresaron misma idea, pero enfatizaron la importancia del entorno que rodea al estudiante para proporcionar las mejores condiciones posibles para el aprendizaje y la aplicación de conceptos matemáticos y afines (^{Montesano y Quiroga, 2020}).

Cabe destacar que la enseñanza o el desarrollo de esta forma de pensamiento debe hacerse a través del juego, ya que demuestran que, a través del juego lúdico, una persona puede seguir cualquier instrucción que le conduzca a un nuevo aprendizaje (^{Morales et al., 2020}; ^{Montesano y Quiroga, 2020}). Otro instructor se hizo eco de estos sentimientos, argumentando que la capacidad de los estudiantes para seguir instrucciones es crucial para su aprendizaje, ya que ayuda en el desarrollo de sus habilidades de pensamiento crítico basado en las matemáticas a lo largo de sus carreras académicas, desde los primeros días de primer año hasta la solución de problemas propios de sus campos de estudio elegidos. En esta secuencia de ideas, según expertos pedagógicos, se destaca que los estudiantes logran comprender la lógica matemática en el marco del desarrollo de conceptos numéricos específicos, como las series, el conteo y la clasificación (^{Sand et al., 2022}).

Enfoques didácticos para fomentar el crecimiento del razonamiento matemático

Aquí se analiza cómo utilizan los profesores sus estrategias para fomentar los procesos de pensamiento lógico matemático. Cabe destacar que todos los artículos analizados coinciden en la importancia de fomentar en los alumnos el desarrollo del pensamiento lógico matemático colocándolos en situaciones de aprendizaje que requieran que dibujen una figura y la coloquen detrás o delante de algo, o haciéndolos trabajar con un conjunto de fichas. Se cree que la puesta en práctica de la observación se logra mediante el uso de tales estrategias, y que los procesos de instrucción y aprendizaje se quedan con esta opción (^{Prieto et al., 2021}; ^{Silva y Bohórquez, 2022}).

Otros autores, sin embargo, sostienen que los alumnos siempre favorecen los análisis abstractos, y que éste es uno de los pocos lugares que cuenta con los recursos pedagógicos y teóricos necesarios para poner en práctica estrategias como el conteo de tacos y la categorización de objetos según su tamaño, color y grosor. Por lo tanto, queda claro el afán del maestro por hacer un uso efectivo de los recursos didácticos que tiene a su disposición. Otra fuente revela que las actividades multigráficas de transcripción de números son la mejor manera de fomentar el pensamiento matemático (^{Thanheiser y Melhuish, 2023}; ^{Trenholm y Peschke, 2020}).

Así, otros estudios han revelado que la aplicación de la estrategia para fomentarla en los alumnos con el fin de que avancen al siguiente nivel de aprendizaje puede variar en función del tipo de planificación que se esté abordando, según los intereses o necesidades del alumno, y que ésta puede implicar el uso tanto de dinámicas de grupo, en función de la variedad de material que se esté manejando, como de actividades en línea (^{Vergel et al., 2020}). Según los resultados de la investigación, es importante tener en cuenta el potencial de los alumnos para trabajar de forma colaborativa y reforzar su aprendizaje, teniendo en cuenta los factores que, según ellos, hay que considerar a la hora de elegir un enfoque para fomentar el desarrollo de la lógica matemática: los intereses, las necesidades y los conocimientos de los alumnos (^{Xu et al., 2021}; ^{Ying y Hsieh, 2017}).

Un profesor expresó su opinión contraria, afirmando que los alumnos aprenden más a través de experiencias prácticas con diversos objetos, lo que les ayuda a desarrollar habilidades como la categorización, la comparación y la lógica. También se propone que el diagnóstico de un punto débil en el proceso del grupo podría obtenerse mediante la observación de los alumnos (^{Karlsson et al., 2022}).

Ante estos hallazgos, es claro que los informantes son conscientes de serias debilidades en la formulación de estrategias pedagógicas para promover el aprendizaje en esta área; esto, sin duda, provoca que las actividades sean monótonas y limitadas a las que se realizan dentro del aula, y reconocen que ésta tiene relativamente pocas herramientas a su disposición con las cuales entusiasmar a los alumnos por aprender (Giacamone et al., 2018).

^{Erkan y Kar (2022}) sostienen que las estrategias de aprendizaje experiencial deben incorporarse como un medio para superar las debilidades comunes que se encuentran en muchos entornos educativos cuando se trata de incorporar materiales pedagógicos en la enseñanza en el aula. Por lo tanto, es un reto para los educadores imaginar nuevos métodos de enseñanza y desarrollo de estas habilidades, lo cual se puede lograr a través de un compromiso serio con la acción educativa, el desarrollo profesional continuo y un enfoque reflexivo de la enseñanza que permita un uso innovador de los recursos y materiales a la mano en ambientes auténticos de aprendizaje (^{Díaz y Díaz, 2018}).

Materiales didácticos y entornos de aula

Esta sección tiene por objeto proporcionar las herramientas de aprendizaje que se utilizan en las aulas para aumentar los conocimientos factuales en un momento y lugar determinados. Los recursos de una estrategia incluyen todo lo que ayuda a ponerla en práctica, como obras de arte, música, juegos, recursos educativos, entre otros. (^{Cronin y Steaert, 2022}).

Por otro lado, se indagó sobre los entornos en los que se desarrollan las estrategias de razonamiento matemático de los estudiantes; los resultados arrojaron que todas las aulas eran buenos lugares para que los alumnos aprendieran estos conceptos. Se estableció claramente que las actividades de refuerzo, como el uso de estrategias didácticas a través del juego en el área de construcción y armamento, y las actividades pedagógicas en el área de expresión y creación, son necesarias para que este aprendizaje se consolide (^{Charalambous et al., 2022}).

Por lo tanto, está claro que la mediación del profesor desempeña un papel crucial durante la utilización de los recursos. Sin embargo, muchos profesores también utilizan otras estrategias para enseñar o lograr la cohesión del grupo sin recurrir a materiales didácticos. Una de estas estrategias consiste en aprovechar cualquier oportunidad didáctica e introducir estas ideas desde el principio de la clase (^{Bozkurt y Yigit, 2022}).

Merece la pena destacar que al plantear la pregunta ¿Cómo puede un estudiante aprovechar al máximo los recursos educativos que tiene a su disposición para potenciar su proceso de aprendizaje?" La respuesta de uno de los entrevistados destaca una estrategia innovadora en la cual se plantea utilizar materiales deteriorados encontrados y, con la colaboración activa de los estudiantes, darles un propósito educativo (^{Berkowitz y Elsbeth, 2022}). Otros propusieron hacerlo mediante el modelado y la interacción del profesor con el alumno, o a través de la mediación, que desempeña un papel crucial, sin dejar de lado que hay que estar dotado de experiencia en la gestión del espacio y de los recursos para llevar a cabo la planificación (^{Alcibar et al., 2018}).

Los resultados en este ámbito arrojan luz sobre las repercusiones de un sistema de formación de profesores que se queda corto a la hora de comprender cómo se desarrolla el razonamiento matemático de los estudiantes pequeños y cuál es la mejor manera de enseñar en esa etapa. En general, los profesores están de acuerdo en teoría en que la incorporación de materiales didácticos eficaces para esta área es crucial, pero en la práctica surgen ciertas deficiencias, que pueden resumirse en el uso de materiales que no resultan especialmente atractivos o motivadores o, en el peor de los casos, en la aplicación incorrecta de una herramienta didáctica eficaz (^{Burgos y Chaverry, 2023}).

Según los resultados de su estudio, la inmensa mayoría de los educadores están mal equipados para enseñar con eficacia debido a la falta de conocimientos o a una formación inadecuada. Esto se refleja en la incapacidad de los profesores para incorporar eficazmente los recursos didácticos a sus planes de clase y a sus esfuerzos pedagógicos, ya que no están seguros de cuál es la mejor manera de estructurar la enseñanza en las distintas materias (^{Cifuentes y Villa, 2017}).

CONCLUSIÓN

El análisis del desarrollo del pensamiento matemático mediante estrategias hermenéuticas demuestra su efectividad para enriquecer la comprensión de los conceptos matemáticos. Estas estrategias facilitan la construcción de significados profundos y establecen conexiones claras entre diversos conceptos, lo que contribuye a una comprensión integral y significativa de las matemáticas.

En cuanto a los enfoques didácticos, las estrategias hermenéuticas resultan fundamentales para potenciar el razonamiento matemático. Al permitir a los estudiantes reflexionar sobre los procesos subyacentes en los problemas matemáticos, estas estrategias estimulan su capacidad de análisis, resolución de problemas complejos y generación de ideas innovadoras. Asimismo, fomentan un pensamiento crítico y creativo al promover la interpretación activa y significativa de los enunciados y contenidos matemáticos.

Respecto a los materiales didácticos y los entornos de aprendizaje, la hermenéutica se posiciona como un enfoque pedagógico clave. Incorporar estas estrategias en el diseño y uso de recursos educativos favorece la interpretación y reflexión sobre los contenidos, enriqueciendo la experiencia de aprendizaje. Esto no solo facilita una comprensión más profunda de los conceptos, sino que también incrementa la participación activa de los estudiantes en su proceso formativo.

En síntesis, las estrategias hermenéuticas son una herramienta valiosa para fortalecer la comprensión, el razonamiento matemático y el diseño de entornos y materiales didácticos efectivos.

CONFLICTO DE INTERESES. No existe conflicto de intereses para la publicación del presente artículo científico.