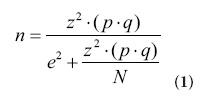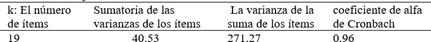Introducción

El mundo actual se caracteriza por su naturaleza globalizada y dinámica, con constantes cambios en las formas de aprender y la continua evolución de las estrategias y enfoques pedagógicos. En este contexto, los sistemas educativos a nivel global han experimentado transformaciones significativas, buscando adaptarse a las demandas de las competencias del siglo XXI y preparar a los alumnos para desafíos futuros (^{Sánchez, 2020}).

A nivel internacional, se observa una tendencia creciente hacia la incorporación del Pensamiento Computacional y Programación (PCP) en los currículos escolares. En países desarrollados y en desarrollo han implementado iniciativas para integrar estos temas en la educación primaria y secundaria.

En países desarrollados, destacan algunas experiencias. Inglaterra, a partir de 2014, incluyó la enseñanza del PCP en el currículum nacional obligatorio, desde la educación primaria hasta la secundaria. Australia, en 2015, implementó el currículum de Tecnologías de la Información y la Comunicación (TIC), que incluye el desarrollo del PCP en todos los niveles escolares. Estados Unidos y Finlandia, desde 2016, lo han integrado de manera transversal en el currículum nacional, enfatizando su aplicación en diferentes áreas del conocimiento.

López et al. (2020), establecen que países en desarrollo también han realizado implementaciones. Por ejemplo, Brasil, a partir del año 2017, publicó lineamientos curriculares que promueven la inclusión de la programación y el razonamiento computacional en la educación básica. India, desde 2018, introdujo el PCP en los planes de educación primaria y secundaria, con un enfoque en el desarrollo de habilidades de resolución de problemas. Además, Sudáfrica, desde 2019, ha realizado esfuerzos por incorporarlo en el sistema educativo, con programas piloto en sus provincias.

Si bien estas iniciativas representan avances significativos, también se han identificado desafíos y oportunidades, como la formación y capacitación docente, la integración curricular efectiva, la disponibilidad de recursos didácticos y tecnológicos, la adaptación de enfoques pedagógicos y la equidad en el acceso y participación de todos los alumnos (^{Márquez, 2019}).

Uno de los principales desafíos es la formación y capacitación docente. Para que la enseñanza del PCP sea efectiva, se requiere que los profesores en formación cuenten con los conocimientos y habilidades necesarias (Lodi & Martini, 2022). Esto implica la necesidad de ofrecer programas de desarrollo profesional que permitan a los docentes apropiarse de estos conceptos y estrategias pedagógicas innovadoras. Otro desafío es lograr una integración curricular efectiva. La incorporación del PCP no debe ser vista como un elemento aislado, sino que debe estar articulado de manera transversal con las diferentes áreas del conocimiento (^{Basogain & Olmedo, 2020}). Lo anterior representa un reto organizativo y desarrollo del plan de estudios en los sistemas educativos. Además, la disponibilidad y accesibilidad de recursos didácticos y tecnológicos adecuados es fundamental. Los centros educativos deben contar con infraestructura, herramientas digitales y materiales de aprendizaje que faciliten el desarrollo de las competencias relacionadas con el PCP.

Finalmente, un desafío crucial es garantizar la equidad en el acceso y la participación de todos los alumnos, independientemente de su contexto socioeconómico, género o antecedentes. Esto requiere acciones específicas para promover la inclusión y reducir las brechas digitales (^{UNESCO, 2020}).

Frente a estos desafíos, también se identifican oportunidades que pueden potenciar la implementación exitosa del PCP en los sistemas educativos. Entre ellas, se destacan: el interés y la motivación de los alumnos hacia las temáticas relacionadas con la tecnología y la programación, lo cual puede ser aprovechado para fomentar el aprendizaje; el desarrollo de habilidades transversales, como la resolución de problemas, el pensamiento crítico y la creatividad, que son fundamentales para el siglo XXI; la posibilidad de establecer alianzas estratégicas entre el sector educativo, la industria tecnológica y la comunidad, para promover iniciativas conjuntas; el surgimiento de experiencias y buenas prácticas a nivel internacional, que pueden ser adaptadas y replicadas en diferentes contextos. (Ruiz- Corbella y García-Gutiérrez, 2020). Abordar estos desafíos y aprovechar las oportunidades identificadas es clave para que la incorporación del pensamiento computacional y la programación en los currículos escolares se traduzca en una mejora significativa de la calidad y la pertinencia de la educación.

En el caso de Chile, el país ha actualizado recientemente sus bases curriculares, incorporando el electivo de PCP, cuyo objetivo es desarrollar habilidades clave como la resolución de problemas, el pensamiento algorítmico y la programación, las cuales se consideran fundamentales para la formación integral de los futuros ciudadanos (^{MINEDUC, 2021}). Para respaldar la implementación de este curso electivo, el Ministerio de Educación (MINEDUC) ha desarrollado diversas iniciativas. Una de ellas, es la realización de capacitaciones docentes a nivel nacional, con el objetivo de que los profesores adquieran los conocimientos y estrategias pedagógicas necesarios para la enseñanza de este curso. Además, puso a disposición de los establecimientos educacionales una variedad de recursos didácticos y materiales de apoyo, tales como guías pedagógicas, unidades de aprendizaje y actividades prácticas. Cabe destacar que la implementación de este electivo se enmarca dentro de una visión más amplia de la transformación digital en la educación, la cual busca preparar a los alumnos para los desafíos y oportunidades del siglo XXI. La implementación exitosa de este nuevo enfoque curricular requiere de docentes preparados e idóneos, capaces de enfrentarse a escenarios exigentes. Estos profesores deben no solo fungir como facilitadores del aprendizaje con apoyo de herramientas tecnológicas (^{Mono, 2023}), sino también poseer los conocimientos y habilidades necesarios para plasmar todo este conocimiento en el desarrollo de competencias en sus alumnos.

El desafío de adquirir conocimientos en temas relacionados con lo digital ha recaído principalmente en los establecimientos educacionales y los profesores encargados de impartir estas disciplinas. Esta situación también es relevante para las universidades que preparan a futuros profesionales, específicamente a los profesores de matemática, quienes deben desarrollar competencias digitales sólidas y transmitirlas efectivamente a sus alumnos. La prueba entonces, acrecentar capacidades en el PCP en los alumnos para la resolución de problemas cotidianos, generar espacios de discusión de las experiencias realizadas, trabajar el pensamiento, ya sea analítico como lógico, y que estos sean innovadoras para conocer el mundo digital de hoy.

Según las bases del PCP ministerial, este desarrolla las competencias necesarias para que los alumnos puedan desenvolverse de manera efectiva en la sociedad digital actual. Busca, además, desarrollar en los alumnos habilidades de imaginación e intuición, donde la tecnología actúa como un apoyo, pero lo más importante es la forma en que esta ayuda a potenciarlas. Lo anterior implica que los profesores deben ser capaces de relacionar adecuadamente los conocimientos disciplinares con las metodologías de enseñanza. Deben elaborar estrategias que estimulen el trabajo colaborativo entre los alumnos (^{Valencia y Panaqué, 2019}). Así, los docentes deben ser comunicadores coherentes con los conocimientos de su disciplina.

Por otra parte, el trabajo de este tema con los alumnos exige a un profesor experto en PCP que se capacite no solamente para utilizar didácticamente las herramientas y aplicaciones en la clase, sino que también desarrollarla como una competencia para desempeñarse en su propia labor docente (^{Zapata-Ros, 2019}).

Se pueden extraer ciertas conclusiones, destacando los argumentos de Vázquez et al., (2019), que el principal desafío de los profesores hoy en día para promover el desarrollo de estas habilidades es, estimular el conocimiento de la materia, apoyadas de estrategias didácticas con resolución de problemas, generación de proyectos, el trabajo interdisciplinario con otras asignaturas del curriculum, tomando en cuenta el contexto y realidades de los alumnos. Sin embargo, la implementación efectiva de estos temas en los sistemas educativos representa un desafío significativo. Diversos estudios como el de ^{Barragán (2023}) han evidenciado que, si bien se han realizado esfuerzos por integrar el PCP, aún existen limitaciones y brechas en su aplicación práctica en las clases. Además, Chile en la actualidad no posee estudios que reflejen si realmente los profesores en formación de la especialidad de matemática están preparados para impartir el electivo descrito anteriormente, para eso, se requieren insumos de información y llevarla a la práctica para las mejoras en el tema.

También, existen brechas en la disponibilidad y accesibilidad a la infraestructura, software y materiales didácticos necesarios para el desarrollo de estas competencias. Ante este panorama, resulta fundamental realizar un estudio exhaustivo que permita comprender en profundidad los desafíos y oportunidades que enfrentan los sistemas educativos en la implementación del PCP. Dicho análisis aportará insumos valiosos para el diseño e implementación de políticas y estrategias que favorezcan una integración más efectiva y equitativa de estas temáticas en los establecimientos educativos del país.

Este estudio también contribuirá a generar conocimiento relevante y actualizado sobre las mejores prácticas a nivel nacional, las cuales pueden ser adaptadas y replicadas en diversos contextos educativos. La justificación de este estudio se basa en la necesidad de fortalecer la incorporación del PCP en la formación inicial docente (FID) y en el sistema educativo en general, de modo que los estudiantes puedan desarrollar competencias digitales y habilidades de resolución de problemas esenciales para su desempeño en el siglo XXI.

En concreto, el estudio tiene como objetivo evaluar si los profesores en formación en matemáticas cuentan con los conocimientos, habilidades y competencias necesarias para impartir de manera efectiva el electivo de PCP en Chile. Para ello, se analizará el perfil de los participantes, se determinará si existen diferencias significativas en las respuestas en función del sexo (hombre o mujer) y se explorarán las correlaciones entre las diferentes variables del cuestionario. Los hallazgos de este estudio proporcionarán información valiosa para fortalecer los programas de la carrera y diseñar estrategias que apoyen a los futuros docentes en el desarrollo de las habilidades necesarias para enseñar eficazmente el electivo. A partir de este contexto, se plantean las siguientes preguntas de investigación que guiarán el análisis: ¿qué nivel de conocimientos previos tienen los futuros profesores sobre PCP?; ¿cómo evalúan su propia preparación para impartir este nuevo electivo?; ¿cuáles son los principales desafíos que enfrentan al intentar enseñar PCP?

Este estudio busca profundizar en la comprensión de la preparación de los futuros docentes en un área crucial para la educación del siglo XXI, con el

objetivo de proponer mejoras en la formación inicial docente.

Referentes Conceptuales

Métodos y materiales

El diseño de investigación propuesto consistió en un tipo descriptivo e inferencial, además de ser transversal, en donde se recolectó datos en un único momento, sin seguimiento a lo largo del tiempo, con el objetivo de examinar y explorar un tema no estudiado previamente, generando información inicial y descriptiva del fenómeno, sin profundizar en sus causas o relaciones, pero iniciando las bases para futuras investigaciones más profundas. (^{Hernández-Sampieri y Mendoza, 2018}).

La investigación se ejecutó durante el primer semestre del año 2023 y su diseño permitió evaluar los conocimientos relacionados con la formación en PCP desde la perspectiva de alumnos de último año de carreras de Pedagogía en Matemática.

Dado el objetivo planteado y el uso de un cuestionario como instrumento de recolección de datos, se optó por una metodología cuantitativa, la cual se justificó por la necesidad de garantizar la precisión y fiabilidad de los resultados obtenidos.

La confiabilidad y la precisión son conceptos clave en la gestión de la calidad de las investigaciones, ya que aseguran la precisión y generalización de los resultados, así como su replicabilidad, tanto interna como externa (Mares, 2019a). Mientras la confiabilidad se refiere a la consistencia de las mediciones, la precisión está relacionada con el grado en que éstas reflejan el valor real del atributo medido. Juntos, estos conceptos garantizan la rigurosidad de los hallazgos, permitiendo que los resultados sean confiables y puedan ser replicados.

Los participantes del estudio fueron conformados por alumnos de último año de las carreras de Pedagogía en Matemática de ocho universidades chilenas, optando por un muestreo no probabilístico de tipo incidental o por conveniencia, el cual se basa en seleccionar a los participantes que están disponibles y son de fácil acceso, en lugar de determinar la muestra mediante un cálculo más cuidadoso (Mares, 2019b).

La representatividad de la muestra fue de aproximadamente el 58%, siendo los cálculos efectuados a través de la Fórmula 1.

n = Tamaño de la muestra

z = Nivel de confianza deseado

p = Proporción de la población con la característica deseada (éxito)

q = Proporción de la población sin la característica deseada (fracaso) e = Nivel de error dispuesto a cometer

N = Tamaño de la población

Sobre una población de 465 alumnos, y fijando un margen de error del 5% y un nivel de confianza del 95%, la muestra intencionada resultante estuvo conformada por 212 participantes. Las edades de los participantes fluctuaron entre los 21 y 30 años, con una media de 25.3 años (D.E = 2.13). La composición de la muestra era del 50% (n = 106) de mujeres y el 50% (n = 106) de hombres.

Para la recogida de información se elaboró un cuestionario ad hoc como instrumento, el cual se diseñó para evaluar los conocimientos de los profesores en formación con relación a su preparación y capacidad de impartir el electivo de PCP. Para su construcción, se tomó en cuenta el programa de estudio PCP, aprobado por decreto exento N°496 del 15 de junio de 2020, ^{MINEDUC (2021}).

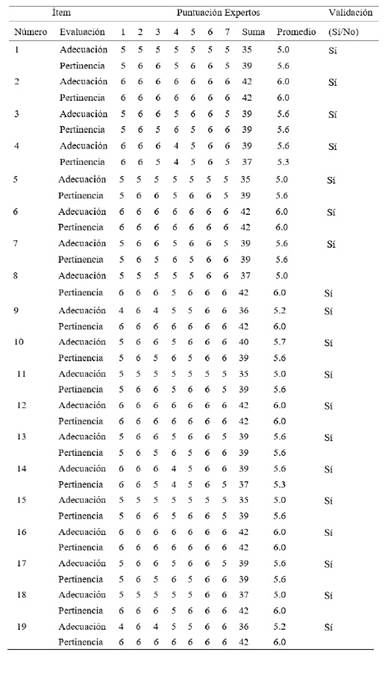
El instrumento de recolección de datos que se utilizó estuvo compuesto por 19 ítems que se muestra en la tabla 1 (variables dependientes) en una escala Likert de 4 niveles (1: Poco, 2: Regular, 3: Bastante y 4: Mucho); adicionalmente, se han incluido algunas cuestiones acerca del perfil de los profesores de matemáticas en formación, tales como género, edad y tipo de universidad. La opción de respuesta a cada ítem se encuentre entre los valores enteros 1 y 4, divididos en seis categorías.

Tabla 1 Preguntas por categoría 

Fuente: Autor (2024)

Para la validación, se recurrió inicialmente al juicio de expertos, aplicando específicamente el método de análisis factorial de Tucker (^{Alban et al., 2020}). Siete doctores de diferentes áreas disciplinares (Matemática, Programación, Didáctica de la Matemática) participaron en este proceso, otorgando, según la tabla 2, un promedio de 5.7 sobre 6 en las categorías propuestas.

Los expertos recomendaron algunos ajustes en redacción y ortografía, resultando en un total de 19 ítems.

Tabla 2 Validación juicio de expertos por cada ítem 

Fuente: Autor (2024)

Asimismo, en la tabla 3 se expone el procedimiento realizado para cálculo de fiabilidad a través del coeficiente alfa de Cronbach, obteniendo un valor general de 0.96 para todas las categorías y preguntas.

Tabla 3 Estadísticos de fiabilidad 

Fuente: Autor (2024)

La interpretación del coeficiente alfa de Cronbach de 0.96 posee un alto nivel de fiabilidad, indicando una excelente consistencia interna entre las categorías y preguntas del instrumento de medición. Esto sugiere que las preguntas están bien alineadas y miden de manera coherente el mismo constructo o concepto. Este alto coeficiente implica que los resultados obtenidos a partir de este cuestionario son confiables y que las preguntas incluidas en el instrumento son relevantes y están bien diseñadas para capturar el constructo que se está evaluando.

La investigación tuvo como propósito evaluar la percepción que tienen los profesores en formación en la disciplina de matemática sobre su nivel de preparación y capacidad para impartir el electivo de PCP. Para ello, la tabla 4 presenta de manera estructurada el procedimiento del estudio, abarcando las distintas etapas y descriptores del proceso investigativo.

Tabla 4 Etapas del estudio 

Fuente: Autor (2024)

Resultados

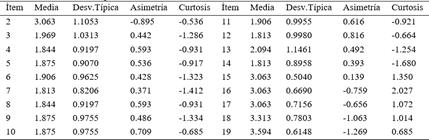
El análisis descriptivo de los datos reveló que los profesores en formación obtuvieron una media superior a 3 en la categoría de habilidades digitales, específicamente en los ítems 15, 16, 17, 18 y 19, según los resultados de la tabla 5. Hay que destacar también que la dispersión de los ítems mencionados anteriormente es baja, lo que significa la no existencia de valores extremos en las respuestas. Esto indica que los participantes poseen conocimientos y un adecuado desarrollo en esta área.

También, los resultados mostraron una media alta (3.06) en la aplicación de conceptos básicos de computación, específicamente relacionados con el ítem 2. Estos resultados proporcionan información valiosa sobre las competencias digitales y el dominio de conceptos computacionales por parte los alumnos, lo cual es relevante, supuestamente, para el desarrollo de sus capacidades en el ámbito del PCP.

Por otra parte, los resultados arrojaron valores en el promedio bajo a 2, todos ellos relacionados con las categorías de resolución de problemas, argumentación-comunicación, modelamiento y representación. Estos bajos valores indican que los alumnos presentan dificultades o un desarrollo insuficiente (poco o regular) en estas competencias clave del PCP.

En lo que respeta a los estadísticos de forma, se destacan los ítems 2, 16, 17, 18 y 19, cuyos valores de asimetría son negativos. Esto indica que los resultados obtenidos se sitúan por debajo del promedio, lo que sugiere que la distribución está sesgada hacia la izquierda. La mayoría de los ítems analizados (2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 y 14) presentan un valor de curtosis negativo. Esto indica que la distribución de los datos en estos ítems tiene una forma más plana y achatada, con los valores más dispersos y menos concentrados alrededor de la media. En contraste, los ítems restantes presentan un coeficiente de curtosis positivo, lo que significa que la distribución de los datos en estos ítems es más apuntada, con una mayor concentración de valores en torno a la media. Lo anterior indica que, en estos últimos ítems, los datos tienden a agruparse más cerca del valor promedio, en comparación con los ítems de curtosis negativa.

Tabla 5 Estadísticos variables dependientes 

Fuente: Autor (2024)

En otro aspecto, antes de realizar la comparación de medias, fue necesario determinar si la distribución de los datos es o no paramétrica. Para ello, se llevó a cabo el siguiente procedimiento: en primer lugar, se calculó el índice de normalidad mediante la prueba de Shapiro-Wilk, cuyos resultados se presentan en la tabla 6. Los resultados mostraron un valor de p superior a 0.05 en todos los ítems, lo que indica que la distribución de los datos sigue una tendencia normal.

Tabla 6 Cálculo del Estadístico W para cada Ítems 

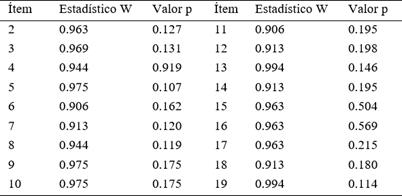
Nota. Si p > 0.05, se puede concluir que el ítem sigue una distribución normal.

Luego, se evaluó la homogeneidad de varianzas mediante la prueba de Levene. Los resultados de la tabla 7 demostraron que todos los ítems presentaban un nivel alto de significancia, lo que confirma que los datos tenían un carácter paramétrico, lo que facilita el uso de técnicas estadísticas más robustas y potentes en el análisis posterior de los datos.

Tabla 7 Cálculo del Estadístico W para cada Ítems 

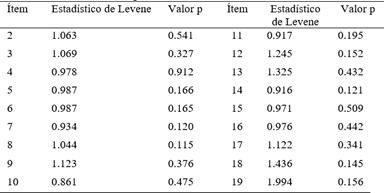
Nota. Si p > 0.05, se puede concluir que no existe diferencia significativa.

Una vez verificados los supuestos de normalidad y homogeneidad de varianzas, se procedió a realizar las comparaciones de medias utilizando la prueba paramétricas t de Student. Para la prueba, se utilizó como variable independiente el sexo del o la estudiante. De acuerdo con los resultados presentados en la tabla 8, no se encontraron diferencias significativas en la variable sexo con respecto a las categorías de resolver problemas y habilidades digitales. No obstante, en el caso de otras tres categorías evaluadas de argumentar-comunicar, modelar y representar, los resultados mostraron niveles de significación óptimos. Esto indica que existen diferencias estadísticamente significativas en las percepciones del estudiantado en función del género para estas tres categorías.

Tabla 8 Nivel de conocimiento por categoría según sexo 

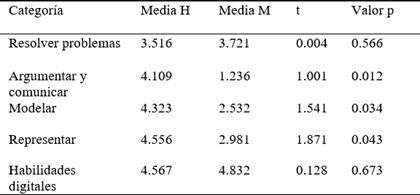
Nota. Si p > 0.05, se puede concluir que existe diferencia significativa.

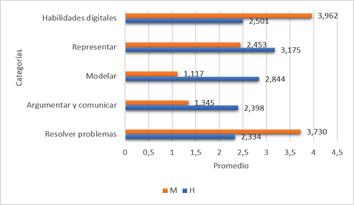
Finalmente, el análisis realizado a través de la prueba de Shapiro-Wilk y la prueba de Levene confirmó que los datos cumplían con los supuestos de normalidad y homogeneidad de varianzas, lo que permitió la aplicación de la prueba t de Student para comparar las medias en función del sexo del estudiante. Los resultados revelaron diferencias significativas en las respuestas entre los grupos de estudiantes masculinos y femeninos en varios ítems, lo que sugiere que el género puede influir en determinadas competencias o percepciones evaluadas. En particular, las categorías de argumentar, comunicar, modelar y representar mostraron diferencias significativas, lo que indica la importancia de considerar el contexto de género en futuras investigaciones y en el diseño de intervenciones educativas. Estos hallazgos destacan la necesidad de profundizar en el análisis de factores que pueden afectar el rendimiento y la experiencia de aprendizaje de los estudiantes, contribuyendo así a una educación más equitativa y adaptada a las diversas necesidades del alumnado. La figura 1 muestra el promedio de conocimiento de los participantes, considerando la variable sexo.

Figura 1 Promedio por categorías según sexo del estudiante 

Según los datos presentados en la figura 1, se observan patrones diferenciados en el nivel de conocimiento percibido por parte de los alumnos en función de su género. En las categorías de resolución de problemas y habilidades digitales, el promedio del conocimiento reportado por las mujeres es ligeramente superior, alcanzando valores cercanos a 4 en ambos casos. Por el contrario, en las otras tres categorías evaluadas argumentar/comunicar, modela y representar, son los hombres quienes presentan promedios más elevados en comparación con las mujeres.

Adicionalmente, se aplicó el coeficiente de correlación de Pearson para analizar las relaciones entre las variables del estudio. Los resultados, presentados en la tabla 9, indican que la mayoría de las correlaciones son positivas, lo que sugiere que, al aumentar el valor de una variable, también tiende a aumentar el valor de la variable asociada.

La correlación positiva leve entre I.2 e I.10 sugiere que, a medida que los futuros profesores se sienten más capacitados para aplicar conceptos de PCP (I.2), también muestran un mayor nivel de habilidad en la creación de aplicaciones y el análisis de problemas (I.10). Esta relación puede interpretarse de la siguiente manera:

- Interconexión de habilidades: la capacidad de aplicar conceptos de PCP facilita el desarrollo de aplicaciones y análisis. Por ejemplo, comprender algoritmos permite a los futuros docentes implementar soluciones prácticas en programación.

- Desarrollo progresivo: la formación en PCP puede estar diseñada para que la aplicación de conceptos preceda a la creación de aplicaciones, lo que explica la correlación entre estas habilidades. A medida que los docentes adquieren confianza en aplicar conceptos, también mejoran en la creación de aplicaciones.

- Efecto de la práctica: la práctica en la aplicación de conceptos contribuye al desarrollo de habilidades más complejas, sugiriendo un proceso de aprendizaje acumulativo.

Así, las correlaciones positivas leves entre I.2 e I.10 reflejan que el dominio de los conceptos básicos de PCP puede fortalecer las habilidades necesarias para desarrollar aplicaciones y realizar análisis. Esta interrelación sugiere que la formación docente debe enfatizar la conexión entre teoría y práctica para mejorar la preparación de los futuros profesores en estas áreas.

La correlación positiva leve entre I.5 e I.13 sugiere que los futuros docentes competentes en la toma de decisiones también tienden a ser más efectivos al evaluar diferentes representaciones. Esta relación puede interpretarse como:

- Interdependencia de habilidades: la toma de decisiones efectiva requiere evaluar diversas representaciones de un problema. Por ejemplo, al abordar un problema de programación, es crucial considerar diferentes representaciones gráficas o lógicas antes de elegir la mejor solución.

- Proceso de análisis: evaluar diferentes representaciones proporciona información valiosa para la toma de decisiones. La capacidad de evaluar representaciones críticamente puede facilitar decisiones más informadas y efectivas.

- Desarrollo de pensamiento crítico: ambas habilidades están relacionadas con el pensamiento crítico. A medida que los futuros docentes desarrollan la capacidad de evaluar representaciones, también mejoran su habilidad para tomar decisiones, siendo más conscientes de las implicaciones de sus elecciones.

Por otro lado, se han identificado correlaciones más fuertes, como:

La habilidad para aplicar conceptos de ciencias de la computación (I.2) está íntimamente relacionada con la capacidad de construir y evaluar estrategias colaborativas (I.3). Los docentes que dominan conceptos técnicos son más efectivos al trabajar en equipo para resolver problemas complejos, integrando su conocimiento en discusiones grupales.

La construcción de estrategias colaborativas (I.3) se correlaciona con la habilidad para construir modelos predictivos (I.8). El trabajo en equipo facilita la identificación de variables relevantes y mejora la calidad de los modelos, enriqueciendo el análisis y la toma de decisiones.

La competencia para colaborar en la resolución de problemas (I.3) está relacionada con el uso responsable de la tecnología (I.17). En entornos colaborativos, los futuros docentes abordan problemas de manera efectiva y son conscientes del uso ético de las herramientas digitales.

La habilidad para tomar decisiones fundamentadas (I.5) se asocia con el uso responsable de la tecnología digital (I.17). Esto implica que los docentes competentes en la toma de decisiones también utilizan la tecnología de forma ética, esencial para preparar a sus estudiantes en un entorno digital. Estas correlaciones más fuertes indican que las competencias en el ámbito del PCP están interconectadas y se refuerzan mutuamente. La formación de los futuros docentes debe enfatizar estas interrelaciones, promoviendo no solo el aprendizaje de habilidades técnicas, sino también la colaboración y la responsabilidad en el uso de la tecnología.

Sin embargo, se han identificado ciertas relaciones que no presentan correlación positiva e incluso pueden sugerir una relación inversa entre algunas variables. A continuación, se explican estas relaciones:

La habilidad para argumentar utilizando lenguaje simbólico y diferentes representaciones (I.6) no se correlaciona positivamente con la capacidad de desarrollar y programar algoritmos (I.7). Esto podría indicar que, aunque un docente tenga habilidades en argumentación, no necesariamente esto se traduce en una mayor competencia en la programación de algoritmos.

La capacidad para construir modelos predictivos (I.8) no muestra correlación positiva con el desarrollo de aplicaciones para dispositivos móviles (I.11). Esto sugiere que, aunque un docente pueda ser competente en modelado teórico, esta habilidad no se refleja en su capacidad para implementar esos modelos en aplicaciones prácticas.

La habilidad para tomar decisiones fundamentadas (I.5) no se correlaciona positivamente con la capacidad de evaluar modelos (I.9). Esto podría reflejar que, aunque un futuro docente sea capaz de tomar decisiones informadas, esta habilidad no necesariamente se traduce en una evaluación crítica de modelos.

La ausencia de correlación positiva, o la posible relación inversa entre estas variables, indica que algunas competencias pueden desarrollarse de manera independiente o en diferentes contextos. Esto resalta la importancia de adoptar un enfoque integral en la formación de futuros docentes, promoviendo la conexión entre habilidades teóricas y prácticas. Es importante destacar que todas las correlaciones reportadas en la tabla presentaron un nivel de significación estadística óptimo (p<0.05), lo que indica que las asociaciones observadas entre las variables tienen una alta probabilidad de no haber ocurrido por azar.

Tabla 9 Coeficiente de correlación entre las variables dependientes de estudio 

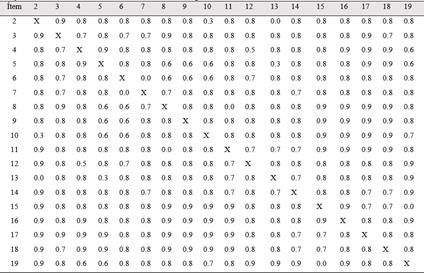
Nota. Se calculó un coeficiente de correlación de Pearson para evaluar la relación lineal entre las variables de estudio. Hubo una correlación positiva entre las variables, r(17) = 0.9, p < 0.001.

El análisis realizado proporciona información valiosa sobre la interrelación entre diversas competencias en el ámbito del PCP y su impacto en la formación docente. Además, resalta la importancia de un enfoque educativo integrado que fomente tanto habilidades técnicas como competencias colaborativas y de pensamiento crítico. También se subraya la necesidad de enfoques pedagógicos que promuevan un aprendizaje más holístico y conectado.

El énfasis en estos resultados en la formación de futuros docentes no solo fortalecerá su preparación técnica, sino que también les dotará de las herramientas necesarias para enfrentar los desafíos del aula contemporánea, garantizando así una educación de calidad en un entorno digital en constante evolución.

Discusión

El objetivo principal de este estudio fue evaluar el nivel de conocimientos sobre procesos cognitivos del PCP desde la perspectiva de estudiantes en los últimos semestres de carreras de pedagogía en matemática. Además, se plantearon objetivos específicos para determinar si existían diferencias significativas en las respuestas según el sexo de los participantes y analizar las relaciones correlacionales entre las diversas variables evaluadas.

Los hallazgos revelaron que la mayoría de los participantes poseen un nivel básico de conocimientos en competencias digitales, pero enfrentan dificultades significativas en competencias clave del PCP, como la resolución de problemas, la argumentación-comunicación y el modelamiento. Este resultado contrasta con estudios previos, como los de ^{Wing (2008}) y ^{Marwa et al. (2024}), que destacan un mayor dominio en estas áreas. La discrepancia sugiere que, a pesar de la formación recibida, persisten brechas en el desarrollo de habilidades cognitivas superiores, como señalan Sánchez y ^{González (2019}). Dado este contexto, es crucial que los programas de formación inicial docente (FID) presten especial atención al refuerzo y equilibrio en el desarrollo de competencias clave del PCP, tal como propone ^{Herrera-Seda (2018}). Además, se deben fortalecer las habilidades digitales y los conceptos computacionales indicados por ^{Quevedo-Sarmiento et al. (2023}), para preparar adecuadamente a los futuros profesores en la enseñanza de la disciplina de manera integral y significativa.

En cuanto a las diferencias de género, aunque no se encontraron diferencias significativas en la resolución de problemas y habilidades digitales, sí se observaron diferencias estadísticamente significativas en las categorías de argumentar-comunicar, modelar y representar. Estos hallazgos sugieren que las percepciones y experiencias de los estudiantes varían en función del género, lo que requiere una exploración más profunda de los factores subyacentes a estas brechas. Investigaciones anteriores, como las de ^{Carrillo-Yáñez et al. (2018}) y ^{Valdivia et al. (2019}), también han señalado la importancia de abordar la inclusión de las mujeres en el ámbito del PCP. Es fundamental diseñar estrategias de intervención y acompañamiento diferenciadas, como proponen ^{Ricci et al. (2019}), para nivelar oportunidades y potenciar el desarrollo equilibrado de todas las competencias, promoviendo así una FID más equitativa e inclusiva.

Por otro lado, la infraestructura tecnológica de las universidades juega un papel crucial en este sentido (^{Martín et al., 2017}). Un acceso limitado a recursos tecnológicos adecuados puede obstaculizar el aprendizaje efectivo del PCP, impidiendo que los estudiantes practiquen y perfeccionen sus habilidades en un entorno realista. Por lo tanto, es fundamental que las instituciones educativas inviertan en infraestructura tecnológica que permita a los estudiantes interactuar con herramientas y plataformas digitales relevantes.

El acceso a recursos educativos también es un factor determinante. La disponibilidad de materiales didácticos actualizados y de calidad puede facilitar el aprendizaje activo y el desarrollo de competencias mencionadas también por ^{Carrillo-Yáñez et al. (2018}). Las universidades deben asegurarse de que los futuros docentes tengan acceso a una variedad de recursos, incluidos cursos en línea, tutoriales y plataformas de programación, que complementen su formación teórica y práctica. Asimismo, el apoyo institucional es esencial para fomentar un entorno de aprendizaje positivo. Programas de tutoría, talleres de capacitación y espacios de colaboración pueden ayudar a los estudiantes a consolidar sus conocimientos y habilidades. La creación de una cultura institucional que valore la innovación y el aprendizaje continuo es clave para preparar a los futuros docentes para los retos del aula contemporánea.

Finalmente, el análisis de correlaciones sugirió que, aunque algunas competencias se desarrollan de manera integrada, hay aspectos que parecen desconectarse o no establecer relaciones significativas entre ellas (^{Simó et al., 2020}; ^{Figueroa-Céspedes et al., 2022}). Este hallazgo es preocupante, ya que sugiere que la formación actual puede no estar promoviendo un desarrollo holístico de las competencias docentes necesarias para la enseñanza del PCP. Es por ello por lo que los resultados de este estudio subrayan la necesidad de revisar y reforzar los programas de FID para abordar las brechas en conocimientos y competencias, así como para fomentar una mayor equidad de género en la formación docente.

Conclusiones

El estudio ha evidenciado que los futuros profesores chilenos de matemática presentan un nivel básico de conocimientos sobre PCP, pero enfrentan importantes desafíos en competencias fundamentales. Este panorama indica que la formación docente actual no está equipando adecuadamente a los estudiantes para abordar de manera efectiva la enseñanza de PCP.

Los hallazgos también revelan diferencias significativas en el desarrollo de competencias según el género, lo que resalta la necesidad de políticas y estrategias específicas que promuevan la inclusión y equidad en la educación. Asimismo, se observó una desconexión entre algunas competencias, lo que sugiere que las metodologías de enseñanza actuales podrían no estar fomentando un aprendizaje cohesivo.

Finalmente, es imperioso que las instituciones de formación docente revisen y mejoren sus currículos para abordar estas brechas y preparar a los futuros educadores de manera más integral. Esta revisión no solo beneficiará a los futuros profesores, sino que también impactará positivamente en la calidad de la enseñanza del Pensamiento Computacional y Programación en el sistema educativo chileno.