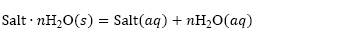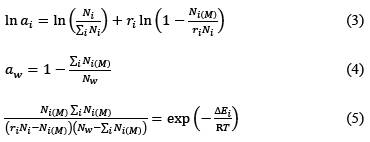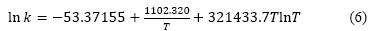Inglés (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
1. Introduction
The use of hydrated salts as phase change material (PCM) for thermal energy storage (TES) is a very attractive solar technological alternative for buildings or other applications. In this case the sun's energy is accumulated by the PCM during the melting process and at night the thermal energy is released due to the crystallization process. A popular practical case that gave rise to this technology is the 135 m2 Dover solar house in Massachusetts, United States, presented by Telkes [1] in 1948, who used the hydrated salt Na2SO4-10H2O as PCM to maintain the interior of the house in thermal comfort (20-24) °C. Currently, PCMs have been integrated into different building components efficiently, for example, in hot water tanks, cold storage using the free cooling method, refrigeration systems, heat pumps, in Trombe walls, pavements, ceilings, windows and blinds [2-5]. This has contributed to energy efficiency in heating and cooling systems of buildings and domestic houses.
Mixtures of eutectic hydrated salts such as PCM play a more attractive role because they do not tend to segregate, have a lower degree of subcooling and phase separation than individual hydrated salts or their non- eutectic mixtures, and in addition eutectic mixtures have a congruent melting temperature [2]. The experimental procedure of designing a eutectic mixture containing inorganic salts consumes significant time and money, even more so when a certain melting point is sought, for example, for its application in buildings [6,7]. Therefore, the prediction of eutectic mixtures of salts and hydrated salts based on a thermodynamic model of electrolytes turns out to be a good alternative. A model with high predictive capacity for phase diagrams of multicomponent systems is the BET model and has recently been used in the calculation of solubilities [7] and the PCM design of eutectic mixtures of hydrated salts [8,9,10,11].
Recently, a eutectic mixture formed by 96.5 mass % Mn(NO3)2-6H2O and 3.5 mass % NaNO3 was experimentally determined by the differential scanning calorimetry (DSC) method for its application as PCM in buildings [12]. The use of Mn(NO3)-6H2O was not only suggested as PCM for thermal energy storage for cooling systems in the literature [13], but was also used as a source of manganese in the preparation of LiMn2O4 cathode materials for Lithium-ion batteries [14], so the study of the properties of this salt and its mixture are important. Solubility data of the NaNO3-Mn(NO3)2-H2O ternary system at 25 °C were not yet reported in the literature.
The main objective of this work is the experimental determination of NaNO3-Mn(NO3)2-H2O solubility, the predictive analysis with the BET model and its verification by measurements of crystallization and melting behavior of the eutectic mixture in order to establish its application as PCM in the range of thermal comfort in buildings.
2. Experimental part
2.1 Materials
The reagents used in the experimental part of this work were the NaNO3 (purity +99.7 mass %) and Mn(NO3)2-4H2O (purity +98.5 mass %) salts, which were purchased from Winkler and Merck, respectively. Ultrapure water was arranged as the third component of the defined system.
2.2 Solubility measurement
The wet waste method was adopted for the study of solubility of the NaNO3-Mn(NO3)2-H2O system at 25 °C [15,16,17]. Supersaturated mixtures of NaNO3 in Mn(NO3)2-H2O solutions were prepared at different compositions in 50 mL glass flasks. In an analogous but inverse manner, supersaturated mixtures of Mn(NO3)2 in NaNO3-H2O solutions were prepared. To do this, the salts and water were previously weighed on an analytical balance with a precision of +0.0001g. Each of the glass flasks containing the mixtures were closed with a lid and immersed in a thermostatic water bath at 25 °C, which contains a basket to fix the glass flasks and a metal shaft to rotate the entire system. The thermostatic bath has a temperature control of +0.1 °C.
The mixtures prepared above were stirred for 72 h which corresponds to a reasonable equilibrium time to reach solid-liquid phase equilibrium at 25 °C. This time was previously determined by measuring the density of a given mixture as a function of time until the property is constant. After 72 h, the system stops and the mixtures are allowed to decant for 12 h, maintaining a constant temperature. Then, for each solid-liquid mixture, a sufficient portion of liquid is extracted with the help of a syringe and a micro filter (0.45 µm porosity) for the analysis of sodium, manganese and nitrate. The solid phases are left with a little supernatant liquid for analysis in the same elements. Sodium and manganese were analyzed by atomic absorption spectrophotometry with direct air-acetylene flame aspiration, while nitrate by ultraviolet-visible absorption spectroscopy.
2.3 Study of crystallization and melting behavior
For crystallization and melting behavior studies, a typical T-history method was applied [18,19]. For that, 25 g of a homogeneous solution of known eutectic composition at a temperature of 25 °C was prepared and stirred vigorously with a magnetic bar for 18 hours in a 50 mL beaker. The solution is transferred into a 100 mL test-tube and placed in a LAUDA ECO RE 420 thermostatic bath with liquid water and temperature control. K-type thermocouples of +0.5 °C were fixed, one in the center of the eutectic mixture and another in the bath water to record the temperature change automatically by computer. The temperature range was set between 10 °C and 30 °C for the cooling and heating processes of the ternary mixture sample, because the eutectic temperature to be verified should be within thermal comfort.
3. Thermodynamic framework
3.1 Solubility equilibrium equation
Let a system be in solid-liquid equilibrium, where the solid phase is a pure hydrated salt with n water molecules and the liquid phase is an aqueous solution containing several dissolved salts, but saturated with respect to the solute of the solid phase, then the equilibrium of phases at constant temperature can be represented as a chemical reaction:
An equilibrium constant, k, for said equilibrium process is defined in terms of the activity of the anhydrous salt, a Salt, and the activity of water, a w , in the liquid phase:
On the other hand, the equilibrium constant depends only on temperature and can be written functionally as:
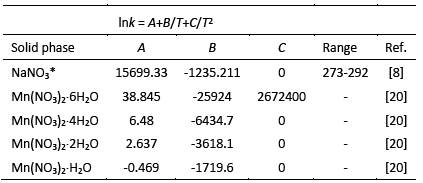
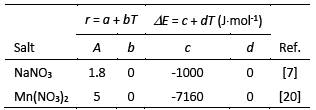
The coefficients A, B and C are given in the literature for various inorganic salts, both hydrated and anhydrous. A compilation of information from the literature for the defined ternary system is given in Table 1.
3.2 BET model
The aSalt and aw activities are determined with the BET model, the equations were formulated from statistical mechanics by Ally and Braunstein [9], the model is formed by three recurrence equations: an equation for the natural logarithm of the activity of a given ith salt, another for the activity of water and finally a constraint commonly called the energy equation.
Where Ni and Nw are the number of moles of the ith salt and water, respectively, N i(M) is the coordination number of water associated with the ith salt, T is the absolute temperature, R is the constant universal of gases, r i and ∆E i are binary model fitting parameters and are corresponding to the ith salt. These parameters depend weakly on temperature and are given in the literature for several inorganic salts. In Table 2, these parameters are given for the salts of the NaNO3-Mn(NO3)2-H2O system at 25 °C and it can be seen that they do not depend on the temperature in this case.
If the solid-liquid equilibrium system contains more than one solid phase, then the above equations are written for each salt. The equilibrium equations and those of the BET model are solved with a numerical method such as the multivariable Newton Raphson method to obtain an approximate resolution of the solubility of the salt in question. This calculation procedure was also explained in several works [7,18,20-23].
4. Results and discussion
4.1 Experimental results
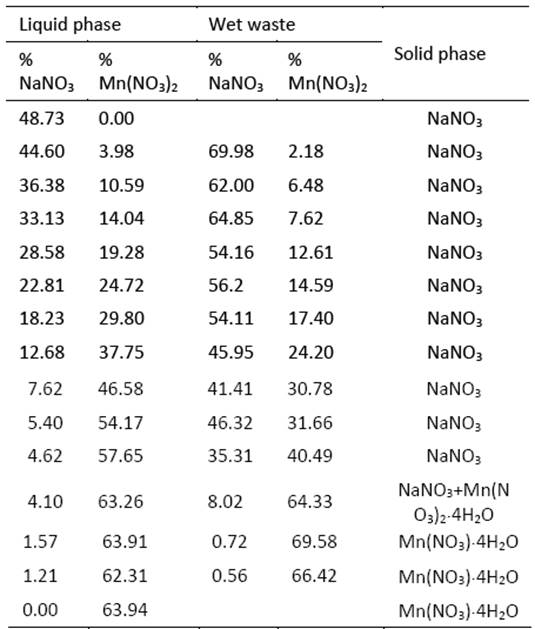
The solubility results of the NaNO3-Mn(NO3)2-H2O system at 25 °C are given in Table 3. The compositions of the liquid phases and wet residue are expressed in mass percentage. The solid phase for each of the cases was determined from the convergence of the equilibrium lines as can be seen in the phase diagram, Figure 1. For each of the points of the saturated solutions and wet residues a line passes straight line that converges to a single point, this is the composition of the solid phase. Therefore, it can be roughly identified that the system forms two solid phases at 25 °C: pure anhydrous sodium nitrate, NaNO3, and pure manganese nitrate tetrahydrate, Mn(NO3)2·4H2O.Additionally, an invariant point can be observed where the projected straight line graphically gives a mixture of crystals, NaNO3+Mn(NO3)·4H2O.
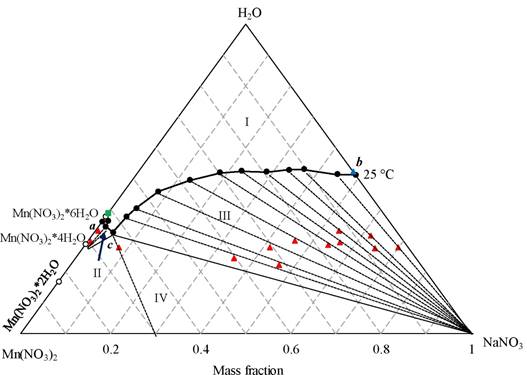
Figure 1. Phase diagram of the NaNO3-Mn(NO3)2-H2O system at 25 °C. (•), Liquid phase composition; (
, 
) data from Linke and Seidell [24] of the NaNO3-H2O and Mn(NO3)2-H2O systems, respectively; (
), wet waste composition. The symbols a and b denote binary points and c the invariant point; I, represents the area of unsaturated solutions, II crystals of Mn(NO3)2·4H2O+solution, III crystals of NaNO3+solution, and IV crystals of NaNO3+Mn(NO3)2·4H2O+solution.
In the phase diagram of the NaNO3-Mn(NO3)2-H2O system at 25 °C constructed with the experimental data obtained, Figure 1, the area above the solubility curve, I, represents the field of existence of solutions unsaturated liquids, region II, saturated liquid solutions in equilibrium with Mn(NO3)2·4H2O crystals, region III, is similar but with NaNO3 crystals, and area IV represents saturated liquid solution in equilibrium with two crystals, a namely, NaNO3+Mn(NO3)2-4H2O. Points a and b represent the binary solubility of the systems Mn(NO3)2-H2O and NaNO3-H2O, respectively, and the point c is an invariant where the system is saturated with both saline solutes. Note that crystallization area II is small compared to area III, this is because Mn(NO3)2-4H2O is more soluble than NaNO3.
4.2 Solubility prediction
The solubility data in Table 3 have an experimental error of approximately 1.1%. In the compendium of Linke and Seidell [24] the solubility data for the binary points are given, that is, for the systems NaNO3-H2O and Mn(NO3)2-H2O at 25 °C. The percentage deviation of the binaries measured in this work with respect to the data of Linke and Seidell are 2.2 % and 4.6%, respectively, and 3.4% with respect to the data of Arrad et al. [25] who also measured solubility data for the binary system Mn(NO3)2-H2O. The wet waste method is a technique that was tested, adopted and applied by several researchers, so the reliability of said experimental method would not be a topic of discussion. In general, the experimental determination of solubility data involves time and money, hence the importance of reducing the number of experimental tests and considering the prediction of solubility data using a thermodynamic model such as the BET model.
Due to the fact that the parameters of the BET model as the equilibrium constants for the NaNO3-Mn(NO3)2-H2O system are known, the model can be used for the analysis of experimental and theoretical results. In this sense, the phase diagram of the binary system Mn(NO3)2-H2O was previously predicted in this work by applying the general calculation procedure described in Section 3; these results are compared with the experimental results given in the literature [24], see Figure 2, both are consistent, they were also demonstrated by Zeng et al [20]. Note that by drawing a horizontal line at 25 °C in the phase diagram (Figure 2), this line is above the calculated eutectic temperature line, 24.3 °C (the experimental one is 24.7 °C). However, the experimental data taken from Linke and Seidell [24], being discrete experimental information, indicate that only the Mn(NO3)2-6H2O phase is formed at 25 °C. As the model provides continuous information, it is known that the system also forms the solid phase Mn(NO3)2-4H2O as can be verified by simple inspection of the phase diagram.
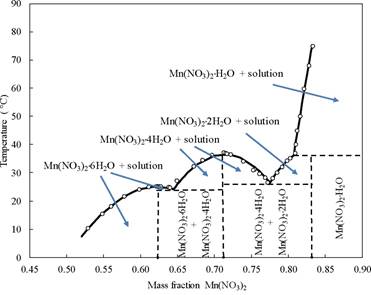
Figure 2. Solubilities of the Mn(NO3)2-H2O system. (o), Experimental data from Linke and Seidell [24]; (-) Calculated with the BET model in this study.
In relation to the binary system NaNO3-H2O, a segment of the solubility curve as a function of temperature was predicted using the BET model with the parameters of Tables 1 and 2, see the results in Figure 3, where it is observed graphically a notable deviation, so in this work the coefficients of the equilibrium constant for NaNO3 in the range of 0 °C to 50 °C were re-estimated, using the least squares criterion using the experimental solubility data of the system binary and equilibrium model. The correlation equation is given in equation (6). In Figure 3, you can see the new calculated solubility curve, which gives a better graphic representation of the experimental data in the considered range. This range is of interest because it includes the solubility study temperature, 25 °C, for the ternary system NaNO3-Mn(NO3)2-H2O and a range where eutectic temperatures may exist close to the thermal comfort temperature in residential areas with PCM of hydrated inorganic salts.
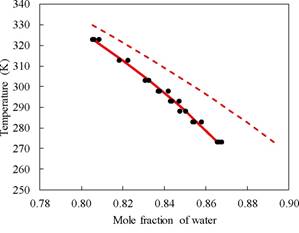
Figure 3. Solubilities of the NaNO3-H2O system. (•), Experimental data from Linke and Seidell [24]; (--), calculated with the BET model using equilibrium constant coefficients from [8] in this study; (-), Calculated with the BET model using re-adjusted equilibrium constant coefficients; both in this study.
Once the parameters of the equilibrium model were defined, the prediction of solubility of the ternary system NaNO3-Mn(NO3)2-H2O at 25 °C was carried out. The results calculated with the BET model agree with the experimental information as can be seen in Figure 4. Note that the solubility branch for the solute Mn(NO3)2 corresponds to the solid phase Mn(NO3)2-4H2O instead of Mn(NO3)2-6H2O, this is because convergence of the model was found considering the tetra-hydrate. This situation is also supported by experimental information where the projection of the equilibrium lines tend to the solid phase Mn(NO3)2-4H2O. The invariant point was predicted with the model, 3.43 % NaNO3 and 63.09 % Mn(NO3)2, very close to the experimental 4.10 % NaNO3 and % 63.26 Mn(NO3)2. Both model and experimental results show a decrease in the solubility of NaNO3 and Mn(NO3)2 salts as an effect of the common ion NO3 -.
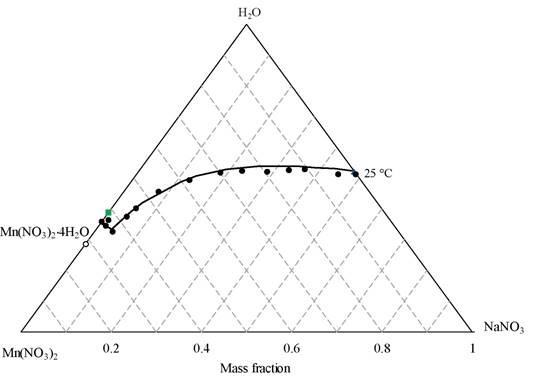
Figure 4. Solubilities of the NaNO3-Mn(NO3)2-H2O system at 25 °C. (•), Experimental data in this study; (, ), experimental data from Linke and Seidell [24]; (-), Calculated with the BET model in this study.
4.3 Eutectic mixture
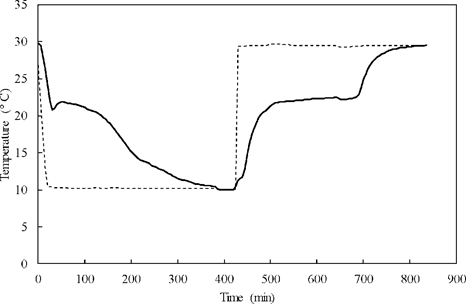
The BET model was also used for the prediction of the polythermal curve and the determination of eutectic mixtures in the thermal comfort range, see Figure 5. In this case, it was possible to find a eutectic mixture with a mass composition of 3.82 % NaNO3 and 96.18 % Mn(NO3)2-6H2O, and a temperature of 22.6 °C (see point e1 in Figure 5), which could be a potential candidate as PCM for thermal comfort in residences. This mixture composition determined with the model is very close to the experimental one (3.5 % NaNO3, 96.5 % Mn(NO3)2-6H2O, and T = 22 °C) which was determined by Schmit et al. [12] who used the DSC experimental method. On the other hand, the method described in Section 3 was used in this study and the calculated eutectic temperature was verified, giving an experimental value between 21 and 23 °C. Said experimental result is shown in Figure 6.
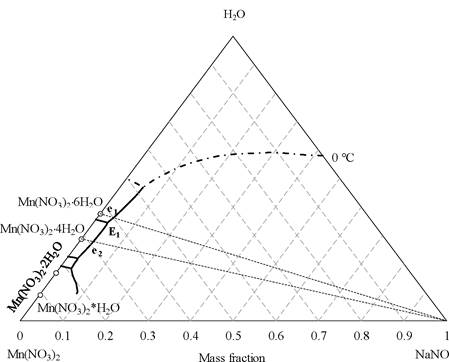
Figure 5. Polythermal solubility curve of the NaNO3-Mn(NO3)2-H2O system. (-·-), isotherm at 0 °C; e1, E1, and e2 are eutectic points; all calculated with the BET model in this study.
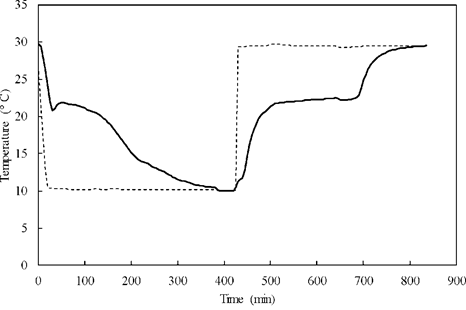
Figure 6. Temperature change curve of PCM and water in the NaNO3-Mn(NO3)2-H2O system. (-), eutectic mixture; (--), water.
5. Conclusions
Solubility data of the NaNO3-Mn(NO3)2-H2O ternary system at 25 °C were measured with the traditional wet residue method. The system forms two crystalline phases: the anhydrous NaNO3 and the hydrate Mn(NO3)2-4H2O, and an invariant point was identified. According to the phase diagram, the crystallization field of Mn(NO3)2-4H2O is very small compared to that of NaNO3.
The BET model was used to predict solubility of the NaNO3-Mn(NO3)2-H2O ternary system at 25 °C, which were consistent with the experimental data. Both the experimental and calculated solubility of each of the salts decreases with the concentration of the other salt due to the common ion effect. For the satisfactory prediction of solubility, it was necessary to re-adjust the coefficients of the correlation of the equilibrium constant with temperature with solubility data of the binary system NaNO3-H2O in the range of 0 °C to 50 °C.
The polythermal curve was also determined with the BET model and a potential eutectic mixture for thermal comfort in residences was estimated. The eutectic temperature was 22.6 °C and was verified experimentally with measurements of the crystallization and melting behavior of the predicted eutectic mixture, the measured value was in the range of 21 °C to 23 °C.
The results found in this study are useful for the simulation of separation processes by crystallization of nitrate salts and/or the study in more detail of a potential PCM candidate of hydrated salts for thermal comfort in residences.
