ENSEÑANZA DE LA FÍSICA

 

SIMULACION DEL MOVIMIENTO DE UN PÉNDULO DOBLE EN UN MEDIO VISCOSO

SIMULATION OF THE MOVEMENT OF A DOUBLE PENDULUM IN A VISCOUS MEDIUM

 

E. MARAZ¹ & O. BURGOA²
Facultad de Ingeniería y Arquitectura - La Paz
Universidad Privada Boliviana
¹erickmaraz@gmail.com    ² osmanburgoa@lp.upb.edu

 

 

---

Resumen

Se presentan las ecuaciones de movimiento de un pendulo doble con una resistencia proporcional a la velocidad usando el formalismo lagrangiano (este sistema de pendulo doble se simula con el lenguaje "yabasic"). Se resuelve dichas ecuaciones utilizando el metodo numérico de Runge-Kutta; como resultado se calcula el coeficiente de resistencia del medio mediante datos experimentales tomando como referencia un pendulo simple.

Codigo(s) PACS: 45.20.Jj — 02.60.Cb

Descriptores: Mecanica lagrangiana y hamiltoniana - Simulación numérica; solución de ecuaciones.

---

Abstract

We present the movement equations of a double pendulum with a resistance proportional to the velocity using the lagrangian formalism (the double pendulum system is simulated with the "yabasic" language). We solve these equations using the Runge-Kutta numerical method; as a result, we calculate the resistance coefficient of the medium using experimental data taken from a simple pendulum as a reference.

Subject headings: Lagrangian and Hamiltonian mechanics — Numerical simulation; solution of equations

---

 

 

1. INTRODUCCION

1.1. Mecánica lagrangiana

La mecanica lagrangiana es una reformulación de la mecanica clásica introducida por Joseph Louis Lagrange en 1788. En la mecanica lagrangiana, la trayectoria de un objeto es obtenida encontrando la trayectoria que minimiza la accion, que es la integral del lagrangiano en el tiempo; siendo este la energía cinetica del objeto menos la energía potencial del mismo.

La utilidad de la formulacion lagrangiana se aprecia incluso en ejemplos sencillos. Por ejemplo, considere una cuenta en un aro. Si se calculara el movimiento de la cuenta usando la mecanica newto-niana, se obtendrıa un sistema complicado de ecuaciones que considerarían las fuerzas que el aro ejerce en la cuenta en cada instante.

En cambio, en la aproximacion de Lagrange, uno mira todos los movimientos posibles que la cuenta podría tomar en el aro y encuentra matematicamente el que reduce al mínimo la accion. Hay muy pocas ecuaciones puesto que no se esta calculando directamente la influencia del aro en la cuenta en un instante dado.

Otro ejemplo es el caso del estudio de movimientos referidos a un sistema que gira, como por ejemplo observaciones astronomicas vistas desde el planeta Tierra: en la formulacion newtoniana es necesario introducir a mano las fuerzas ficticias o fuerzas de inercia como la fuerza centrífuga o la fuerza de Cori-olis mientras que en la formulacion lagrangiana estas fuerzas aparecen de modo natural.

Los dos problemas considerados anteriormente son mucho mas sencillos de resolver empleando la formulacion lagrangiana (Wikipedia 2014a).

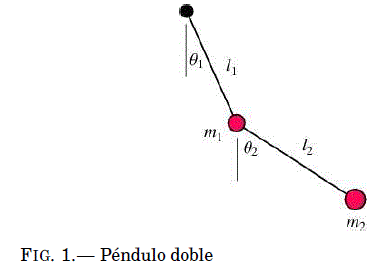
1.2. Péndulo doble

En general, un doble pendulo es un sistema compuesto por dos pendulos, con el segundo colgando del extremo del primero. En el caso mas simple, se trata de dos pendulos simples, con el inferior colgando de la masa pendular del superior.

Normalmente se sobreentiende que nos referimos a un doble pendulo plano, con dos péndulos planos coplanarios. Este sistema físico posee dos grados de libertad y exhibe un rico comportamiento dinamico. Su movimiento esta gobernado por dos ecuaciones diferenciales ordinarias acopladas (Wikipedia 2014b).

 

2. METODOLOGÍA

2.1. Ecuaciones de Euler-Lagrange para un péndulo doble

De acuerdo a la Figura 1 se determina las posiciones de las masas del pendulo doble:

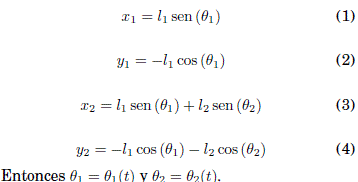
La energía potencial y cinetica del sistema son:

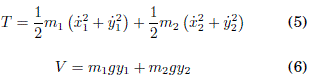
Reemplazando (1), (2), (3) y (4) en las ecuaciones (5) y (6) se obtiene:

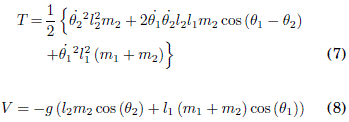
La lagrangiana se expresa como:

Sustituyendo los valores de las ecuaciones (7) y (8) en (9) se consigue la funcion lagrangiana:

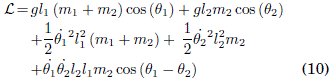
Considerando que el coeficiente de resistencia tiene la forma podemos formular las siguientes ecuaciones de Lagrange para este caso:

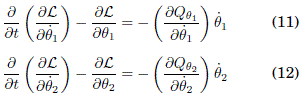
Desarrollando las ecuaciones (11) y (12) se obtiene un sistema de ecuaciones diferenciales no lineales de segundo orden:

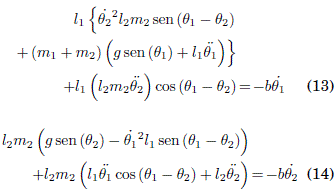
2.2. Cálculo del coeficiente b mediante un péndulo simple

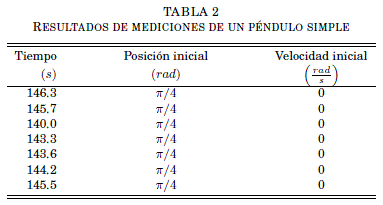
Para el calculo de este coeficiente se realizaron mediciones del tiempo que tarda un pendulo simple que comienza su trayectoria en reposo a 45° hasta que ya no sobrepasa los 5^o. En la Figura 2 se muestra el sistema utilizado. Las Tablas 1 y 2 muestran los datos y resultados.

Este coeficiente se obtuvo con el promedio del tiempo necesario. Los modelos empleados para su calculo tienen la forma de las ecuaciones (11) y (12).

2.3. Método Runge Kutta

Este es el método numérico que se utiliza para el calculo de θ₁ y θ₂ donde h es la tolerancia, f y g funciones que dependen de las velocidades v_x,v_y; distancias x,y y tiempo t (Neumann 2010).

Las condiciones iniciales son x(0), y(0), v_x(0), v_y(0) que representan posiciones y velocidades respectivamente:

f(x,y,vx,vy,t)
g(x,y,vx,vy,t)
k1=h*vx0;
l1=h*f(x0,y0,vx0,vy0,t);
q1=h*vy0;
m1=h*g(x0,y0,vx0, vy0,t);
k2=h*(vx0+l1/2);
l2=h*f(x0+k1/2,y0+q1/2,vx0+l1/2,vy0+m1/2,t+h/2);
q2=h*(vy0+m1/2);
m2=h*g(x0+kl/2,y0+q1/2,vx0+l1/2 ,vy0+m1/2,t+h/2);
k3=h*(vx0+l2/2);
l3=h*f(x0+k2/2,y0+q2/2,vx0+l2/2,vy0+m2/2,t+h/2);
q3=h*(vy0+m2/2);
m3=h*g(x0+k2/2,y0+q2/2,vx0+l2/2 ,vy0+m2/2,t+h/2);
k4=h*(vx0+l3);
l4=h*f(x0+k3 ,y0+q3,vx0+l3 ,vy0+m3,t+h);
q4=h*(vy0+m3);
m4=h*g(x0+k3,y0+q3,vx0+l3,vy0+m3,t+h);
vx=vx0+(l1+2*l2+2*l3+l4)/6;
vy=vy0+(m1+2*m2+2*m3+m4)/6;
x=x0+(k1+2*k2+2*k3+k4)/6;
y=y0+(q1+2*q2+2*q3+q4)/6;

 

3. RESULTADOS

3.1. Modelo computacional y simulación

Se realizo un programa en el lenguaje yabasic que permite la visualizacion de un péndulo doble en un medio viscoso, en este caso el aire.

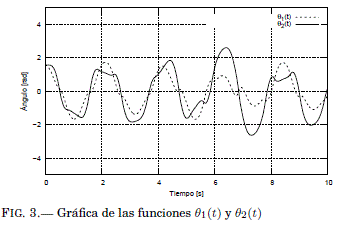
El método Runge Kutta se realiza dentro de un bucle, esto se puede observar entre las líneas 21 y 55 del script del Codigo 1 y la gráfica de los resultados del calculo se pueden apreciar en la Figura 3. Los datos de la Tabla 1 se presentan entre las líneas 10 y 20 del mismo script. Algunas escenas de la simulacion se muestran en la Figura 4.

1 open window 500,500
2 window origin "cc"
3 sub f(x,y,vx,vy,t,b,m1,m2,g,l1, l2) :
4      return (2*b*l1*vy*cos(x - y)
       - l2*(2*b*vx + g*l1*(2*m1
       + m2)*sin(x) + l1*m2*(g*sin(x
       - 2*y)+2*l2*vy**2*sin(x - y)
       + l1*vx**2*sin(2*(x - y)))))
       /(2*l1**2*l2*(m1 + m2 - m2
       *cos(x - y)**2))
5 end sub
6 sub g(x,y,vx,vy,t,b,m1,m2,g,l1,l2):
7      return (-2*l2*m2*cos(x - y)
       *(b*vx + l1*l2*m2*vy**2*sin(x - y))
       + 2*l1*(m1 + m2)*(b*vy
       - l2*m2*(l1*vx**2 + g*cos(x))
       *sin(x - y)))/(l1*l2**2*m2*(-2*m1
       - m2 + m2*cos(2*(x - y))))
8 end sub
9 h=0.01
10 b=6743.89 rem coeficiente b
11 mo1 = 88.5 rem masa del primer pendulo
12 mo2 = 88.5 rem masa del segundo pendulo
13 g=981.0 rem aceleracion de la gravedadrem
14 x0 = pi/2.0 rem condicion inicial de posicion en el eje x
15 y0 = pi/2.0 rem condicion inicial de posicion en el eje y
16 vx0 = 0.0 rem condicion inicial de la velocidad en el eje x
17 vy0 = 0.0 rem condicion inicial de la velocidad en el eje y
18 lo1 = 50.0 rem longitud del primer pendulo
19 lo2 = 50.0 rem longitud del segundo pendulo
20 radio = 3.0
21 while(1)
22      clear fill circle lo1*sin(x0),lo1*cos(x0),radio
23      clear fill circle lo1*sin(x0)+lo2*sin(y0),lo1*cos(x0)+lo2*cos(y0),radio
24      clear line 0,0,lo1*sin(x),lo1*cos(x)
25      clear line lo1*sin(x),lo1*cos(x),lo1*sin(x)+lo2*sin(y),lo1*cos(x)+lo2*cos(y)
26      k1=h*vx0
27      l1=h*f(x0,y0,vx0,vy0,t,b,mo1,mo2,g,lo1,lo2)
28      q1=h*vy0
29      m1=h*g(x0,y0,vx0,vy0,t,b,mo1,mo2,g,lo1,lo2)
30      k2=h*(vx0+l1/2)
31      l2=h*f(x0+k1/2,y0+q1/2,vx0+l1/2 ,vy0+m1/2,t+h/2,b,mo1,mo2,g ,lo1,lo2)
32      q2=h*(vy0+m1/2)
33      m2=h*g(xO+kl/2,yO+ql/2,vxO+l1/2,vy0+m1/2,t+h/2,b,mo1,mo2,g,lo1,lo2)
34      k3=h*(vx0+l2/2)
35      13=h*f(x0+k2/2₍y0+q2/2,vx0+l2/2,vy0+m2/2,t+h/2,b,mo1,mo2,g,lo1,lo2)
36      q3=h*(vy0+m2/2)
37      m3=h*g(x0+k2/2₍y0+q2/2,vx0+l2/2,vy0+m2/2,t+h/2,b,mo1,mo2,g,lo1,lo2)
38      k4=h*(vx0+l3)
39      l4=h*f(x0+k3 ,y0+q3,vx0+l3,vy0+m3,t+h,b,mo1,mo2,g,lo1,lo2)
40      q4=h*(vy0+m3)
41      m4=h*g(x0+k3 ,y0+q3,vx0+l3,vy0+m3,t+h,b,mo1,mo2,g,lo1,lo2)
42      vx=vx0+(l1+2*l2+2*l3+l4)/6.0
43      vy=vy0+(m1+2*m2+2*m3+m4)/6.0
44      x=x0+(k1+2*k2+2*k3+k4)/6.0
45      y=y0+(q1+2*q2+2*q3+q4)/6.0
46      line 0,0,lo1*sin(x),lo1*cos(x)
47      line lo1*sin(x),lo1*cos(x) ,lo1*sin(x)+lo2*sin(y),lo1*cos(x)+lo2*cos(y)
48      fill circle lo1*sin(x),lo1*cos(x) ,radio
49      fill circle lo1*sin(x)+lo2*sin(y) ,lo1*eos(x)+lo2*cos(y),radio
50      x0=x
51      y0=y
52      vx0=vx
53      vy0=vy
54      wait(0.0001)
55 wend

CODIGO 1: Script en lenguaje yabasic.

 

4. ANALISIS Y DISCUSIÓN

En base a un pendulo simple se calculó el coeficiente b (vease Tabla 1), dato que se utilizó en un sistema de dos pendulos ya que las funciones utilizadas con las ecuaciones de Euler Lagrange para la resolucion de un péndulo simple en un medio viscoso mostraron un comportamiento muy cercano al del sistema armado (vease Figura 2).

En el calculo del coeficiente b se observo que no puede existir una mayor precision porque no cumplen las condiciones necesarias, esto puede ser causado por las unidades de los datos. Este coeficiente debido a las unidades puede significar muchas posibilidades, puede depender directamente del area de la esfera ya que esta en un medio viscoso (en este caso el aire), masas, longitudes, aceleracion de la gravedad y otros. Con una mayor cantidad de experimentos con diferentes longitudes, masas, radios, aceleracion de gravedad se podría conocer si b es un coeficiente dependiente de los datos para cada caso o una constante para todos los casos en sistemas de pendulos. Un aspecto importante a tomar cuenta es que para este modelo las cuerdas tiene que ser barras solidas que impidan una alteración en la longitud de estas.

El analisis de las energías, posiciones, velocidades, etc. sugiere un estudio mas especializado en dinamica no lineal y caos en el cual un péndulo doble siempre es un excelente ejemplo (Strogart 1994).

 

5. CONCLUSIONES

Las ecuaciones de Euler-Lagrange describen el movimiento de un pendulo doble correctamente y el metodo numérico Runge Kutta nos permite simularlo.

El coeficiente b (vease Tabla 1) calculado lleva mucha informacion dentro ya que esta constante puede depender directamente de la longitud, aceleracion de gravedad, radio, area y masa del sistema por lo cual una simulacion con diferentes datos de longitud y masa podrían ser alejados a la realidad. Se utilizo el sistema de unidades cegesimal para una mayor precision en el valor de 6.

 

REFERENCIAS

Neumann E. (2010), http://www.myphysicslab.com/rungekutta.html        [ Links ]

Strogart S. H. (1994), Nonlinear Dynamics and Chaos (Perseus Books)        [ Links ]

Wikipedia. (2014a), http://es.wikipedia.org/wiki/Mecánica_lagrangiana         [ Links ]

(2014b), http://es.wikipedia.org/wiki/Doblependulo        [ Links ]