Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
uBio 
Permalink
INTRODUCCIÓN
Los pesticidas son muy utilizados para el control de plagas y enfermedades en la agricultura. Sin embargo, el uso indiscriminado y la manipulación inadecuada pueden desencadenar problemas en la salud humana y el ambiente1. La toxicidad de los pesticidas constituye un peligro para las personas que se exponen a dichas sustancias debido a su volatividad, unos más que otros2),(3, y afecta directamente a la salud de las personas principalmente por inhalación. Es importante conocer la presión de vapor de los pesticidas, puesto que una sustancia con alta presión de vapor resulta altamente toxica4),(5),(6),(7.
Existen pesticidas cuyos valores de presión de vapor no han sido determinadas experimentalmente por varias razones, entre ellas, su alta toxicidad, el alto costo económico y las condiciones de operabilidad8. Sin embargo, ésta puede estimarse mediante la obtención de modelos matemáticos predictivos QSPR (relaciones cuantitativas estructura propiedad)9. Es necesario subclasificar los pesticidas por similitud estructural para obtener modelos más precisos, trabajar con grupos de pesticidas reduce la complejidad y la dimensionalidad del problema y contribuye a una comprensión más profunda de los factores que influyen en la presión de vapor y mejora la interpretación de los modelos10. Comprender las similitudes estructurales permite el diseño racional de nuevos pesticidas. La subclasificación ayuda a identificar patrones estructurales que están asociados con propiedades específicas e induce al desarrollo de compuestos más seguros y efectivos; además, mejora la comprensión de los riesgos asociados con la exposición a estos compuestos químicos.
En el presente trabajo se emplea un conjunto de datos de la presión de vapor de 1005 pesticidas estructuralmente diversos. Para la subclasificación en función de la similitud estructural y presión de vapor, se utilizan los datos de presión de vapor experimentales conocidos a 20°C de una base de datos de propiedades de pesticidas (PPDB) disponible en la literatura.
Una etapa crucial en el análisis de moléculas químicas, mediante técnicas de quemo-informática es el cálculo de descriptores moleculares. Estas metodologías permiten representar cada estructura molecular como un vector numérico en un espacio de descriptores. Existen distintos programas que permiten calcular descriptores moleculares.
Entre los más conocidos se tiene al PaDEL-Descriptor (v. 2.20) que es una herramienta de software de código abierto que proporciona una amplia gama de descriptores moleculares, incluyendo descriptores 1D, 2D y 3D; se utiliza ampliamente en el campo de la quemo-informática y es fácil de usar. ISIDA/Fragmentor es un descriptor que cuenta tipos de átomos y fragmentos de subestructuras lineales que van desde 1 a 5 átomos de longitud. RDKit es una colección de herramientas de código abierto para la quemo-informática y la minería de datos químicos. Dragon es un software comercial que ofrece una amplia gama de descriptores moleculares, incluyendo descriptores 1D, 2D y 3D, es conocido por su amplia variedad de descriptores y su capacidad para manejar grandes conjuntos de datos.
En el presente trabajo se utilizó el programa PaDEL-Descriptor por ser una herramienta versátil y accesible que permite a los investigadores calcular una amplia gama de descriptores moleculares para análisis químico y modelado predictivo11.
Las estructuras moleculares son elementos complejos, y los diferentes programas ya mencionados hacen uso de una gran cantidad de descriptores para poder caracterizar cada molécula de una manera más completa. Sin embargo, el análisis de datos descritos en espacios de múltiples dimensiones tiende a engendrar diferentes problemas que llevan el nombre de “maldición de la dimensión” (12),(13. En este contexto, uno de los problemas más importantes es el de la perdida de utilidad de diferentes medidas de distancia. En efecto, si uno desea caracterizar la estructura de un conjunto de datos mediante el cálculo de las distancias entre distintos pares de objetos, la tendencia general es que la diferencia entre dichas distancias tiende a disminuir cuando aumenta la dimensionalidad del espacio de descriptores. En este caso, la calidad de técnicas clásicas de análisis de datos, como el agrupamiento de objetos o clustering, tienden a disminuir, y diferentes métodos han sido propuestos para poder contrarrestar los efectos de la maldición de la dimensión.
El subspace clustering es una técnica de data-mining que tiene por finalidad agrupar objetos descritos numéricamente en un espacio de descriptores para formar grupos llamados clústeres de objetos similares, y para detectar simultáneamente los subespacios de descriptores que caracterizan cada clúster. Esta técnica permite analizar la estructura de un conjunto de datos examinando la similitud entre grupos de objetos descritos en diferentes subespacios14. Diferentes estudios han mostrado que el subspace clustering está particularmente adaptado al estudio de datos en altas dimensiones15, y por ende es un excelente candidato para analizar descriptores moleculares. En efecto, estas técnicas han sido empleadas con éxito para el análisis de moléculas químicas según propiedades fisicoquímicas como la adsorción16.
En este artículo aplicamos con éxito SubCMedians17, un algoritmo de subspace clustering que ha mostrado buenos resultados con respecto a otros algoritmos para agrupar descriptores de diferentes estructuras moleculares pesticidas y analizar la volatilidad de las moléculas contenidas en cada clúster. El resto del artículo se organiza de la siguiente manera: En la sección siguiente se describe el algoritmo SubCMedians así como el conjunto de datos analizados, su preprocesamiento y el protocolo experimental que hemos empleado. En la subsiguiente sección, se describen los resultados obtenidos. Finalmente, se concluye el trabajo resumiendo los puntos centrales del mismo.
EXPERIMENTAL
Materiales y Métodos
El trabajo se inició con 1509 moléculas de pesticidas en formato MDL mol (V2000), mismas que fueron cambiadas de formato de archivo con el programa Open Babel para Windows18. Del total de moléculas, 1005 pesticidas cuentan con valores de presión de vapor y son estructuralmente, diversos19. Los datos de presión de vapor se han obtenido de la base de datos PPDB, que muestra identidad química, fisicoquímica, de salud humana, ecotoxicológicos de plaguicidas y otros. Ha sido desarrollado por la Unidad de Investigación de Agricultura y Medio Ambiente (AERU) de la Universidad de Hertfordshire para una variedad de usuarios finales.
Se puede apreciar que las características del conjunto de datos involucran estructuras muy heterogéneas con composición química variada incluyendo una amplia variedad de elementos químicos en moléculas orgánicas y sales de diferente tamaño. Los compuestos no considerados en el presente análisis son: compuestos poliméricos, como, mancozeb, maneb, metiram. Para el caso de mezclas de isómeros que conducen a una misma estructura topológica, se considera solo uno de ellos, es decir, diclobutrazol.
Las estructuras de los pesticidas que no contaban con su canonical smile se dibujaron con el programa ACDLabs/ChemSketch20 en formato MDL mol (V2000). Los descriptores moleculares se calcularon utilizando PaDEL, un software de código abierto y disponible gratuitamente. El Laboratorio de Exploración de Datos Farmacéuticos (PaDEL-Descriptor (v. 2.20) (21 calcula 14464 descriptores moleculares 0D-2D y tipos de huellas dactilares. Se analizaron los 14464 descriptores moleculares para eliminar descriptores colineales con información redundante.
Pre-procesamiento de los datos
Antes de aplicar la técnica de subspace clustering al conjunto de datos presentado anteriormente, se procedió a aplicar diferentes técnicas de pre-procesamiento: En primer lugar, se procedió a filtrar los descriptores para los cuales la mayoría de las estructuras moleculares no tenían valores. El programa de descriptores moleculares empleado organiza en orden creciente, los descriptores en función del número de valores faltantes que poseen, como se puede evidenciar en la figura 1. En este trabajo se eliminaron todos aquellos descriptores para los cuales menos del 20% de moléculas tenían un valor. Después de esta etapa, solo se conservaron los primeros 126 descriptores.
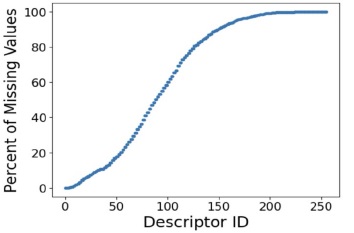
Figura 1: Porcentaje de valores faltantes en cada descriptor. Se filtraron todos los descriptores con más de 80% de valores faltantes.
Posteriormente se procedió a rellenar los valores faltantes con ceros, en este punto, es importante resaltar que las coordenadas de las diferentes estructuras moleculares en el espacio de descriptores corresponden únicamente a valores reales superiores o iguales a cero. Posteriormente se aplicó una transformación logarítmica a los datos, empleando la función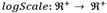 
tal que 
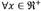, logScale(x) = log10(x + 1). Finalmente se aplicó una normalización Zscore a estos datos, con el fin de que en cada dimensión, las coordenadas de los datos tengan una media igual a cero y una dispersión estándar igual a uno:
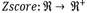tal que 
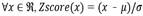, Donde µ y σ representan respectivamente la media y la desviación estándar en la dimensión considerada.
Subspace clustering
SubCMedians
SubCMedians17 tiene por objetivo elaborar un modelo de subspace clustering basado en medianas descritas en subespacios específicos. El uso de medianas provee a este método propiedades interesantes, como ser una intrínseca robustez al ruido y a valores anómalos. Por otra parte, la utilización de subespacios le permite hacer frente a los efectos de la maldición de la dimensión.
El algoritmo recibe como entrada un conjunto de objetos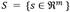 
descritos en un espacio de m dimensiones, y sea D = {d1,…,dm} el conjunto de dimensiones, y tiene por objetivo elaborar un modelo de subspace clustering, definido como un conjunto de medianas candidatas M, en el que cada mediana 
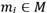está asociada a un subespacio 
. Cada objeto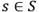 
es asociado al clúster Ci que posee la mediana candidata mi más cercana, es decir a la que minimiza la distancia 
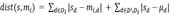, donde mi,d representa la coordenada de la mediana mi en la dimensión d, y µd es la media de las coordenadas de todos los objetos en S en la dimension d (en el caso de un conjunto de datos normalizado por la tecnica de z-score 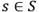). El Error Absoluto de un modelo M con respecto a un objeto 𝑠 se define como 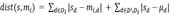la distancia entre el objeto y la mediana más cercana, y por consiguiente la Suma de Errores Absolutos de un conjunto de datos S con respecto a un modelo M se define como 
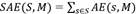. Por otra parte, el tamaño de un modelo M, denominado 
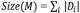es la suma de las dimensionalidades de todos los subespacios asociados a las medianas en M, y corresponde al nivel de detalle capturado por el modelo. SubCMedians tiene por objetivo construir el conjunto de medianas M que minimice la SAE y tal 
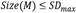, donde SDmax es un parámetro que caracteriza el maximo nivel de detalles que debe poseer el modelo M.
Con el fin de reducir los tiempos de cálculo SubCMedians emplea una muestra dinámica del conjunto de datos Ŝ, de tamaño N, para estimar la SAE del modelo M. El algoritmo inicializa Ŝ tomando N objetos aleatorios en S, y a cada iteracion, un objeto elegido al azar en Ŝ es substituido por otro elemento extraido uniformemente en S/Ŝ, con el fin de modificar la muestra. La SAE del modelo se actualiza de manera incremental substrayendo la AE del objeto eliminado y adicionando la AE del nuevo objeto. Si el error actualizado es superior al anterior, se procede a realizar un intento de optimización del modelo actual, en caso contrario, el algoritmo no realiza ninguna acción.
Con el fin de minimizar la SAE manteniendo la restricción 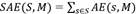, SubCMedians actualiza iterativamente un modelo M, combinando coordenadas de los objetos del conjunto de datos, mediante una tecnica de optimización estocástica de hill-climbing durante Nbiter iteraciones. SubCMedians comienza con un modelo inicial, el modelo vacío (sin medianas) 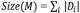cuyo error absoluto a un objeto 𝑠 es 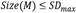. A cada iteración, a partir de un modelo M SubCMedians se produce una variante aleatoria M´, la cual reemplaza al modelo actual M en el caso en el que 
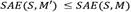. Con el fin de generar una variante M´, SubCMedians emplea una estrategia basada en ponderaciones para guiar su búsqueda local hacia subespacios prometedores. Sea Wi,d el peso asociado a la dimensión 𝑑 para la mediana mi, y sea 
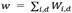el peso total del modelo actual. Si 
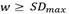el algoritmo procede a elegir al azar un par de índices (i,d) con una probabilidad proporcional a Wi.d , se reduce el peso correspondiente 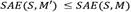y si Wi,d = 0 entonces se elimina la coordenada correspondiente en la mediana seleccionada 
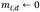. A continuación, SubCMedians selecciona aleatoriamente un objeto 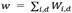y una dimensión 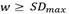, y selecciona una mediana c con una probabilidad proporcional a su suma de pesos correspondientes 
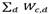, o genera una nueva mediana con una probabilidad igual a 1/w, finalmente se modifica la coordinada de la mediana en cuestión 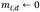y se incrementa el peso asociado 
.
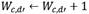Una vez que el algoritmo ha completado Nbiter iteraciones, se genera un modelo de subspace clustering asociando cada objeto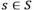 
al clúster Ci que posee la mediana candidata mi más cercana (la que minimiza la AE). Si varias medianas minimizan la AE, entonces se elige una de forma no determinista. Si una mediana no posee ningún objeto asociado, entonces no da lugar a un clúster.
Modelo de fusión
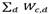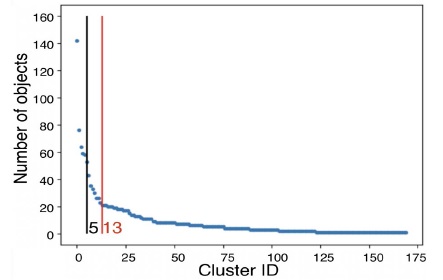
Con el fin de tener un modelo más robusto y de mejor calidad, se procedió a utilizar SubCMedians para producir un conjunto de 100 modelos de subspace clustering independientes {M1,M2,…,M100}. En cada ejecución se utilizaron los mismos parámetros SDmax = 300, N = |S|, y Nb = 10,000. Posteriormente se fusiónaron los diferentes modelos en uno solo , se procedió a formar clústeres agrupando los objetos en el conjunto de datos entorno a las medianas de M y se contabilizó el número de objetos |Ci| en cada clúster Ci asociado a cada mediana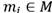 
. Finalmente se conservaron las k medianas con mayor número de objetos asociados para formar un nuevo modelo M* que se optimizo durante 10,000 nuevas iteraciones. Este procedimiento permite una mejor exploración del espacio de modelos posibles, seleccionando las k medianas que mejor describen los datos, esto es entre un conjunto de medianas generadas por 100 modelos independientes. Con el fin de determinar el número k de medianas que debían conservarse, representamos el número de objetos contenidos en cada clúster en orden decreciente, y utilizamos el método de codo para determinar el número de medianas a partir del cual la cantidad de objetos en los clústeres se estanca con valores más bajos. En la figura 1 podemos apreciar que a partir de 13 medianas los clústeres tienden a poseer menos objetos y a ser por ende menos representativos. Por consiguiente, decidimos conservar las k = 13 medianas con más objetos asociados para crear el modelo de fusión.
Visualización
Para visualizar la estructura del conjunto de datos analizados, empleamos el algoritmo T-distributed stochastic neighbor embedding (t-SNE) (22. Este algoritmo de reducción de dimensionalidad permite proyectar de manera no lineal, datos de alta dimensión a un plano bidimensional, de tal manera que objetos similares en el espacio de alta dimensionalidad tienden a ser representados mediante puntos cercanos en el plano bidimensional, mientras que objetos disímiles tienden a representarse distantes entre sí en el plano. Antes de aplicar este método, como lo sugieren sus autores, empleamos el método de reducción de dimensionalidad lineal llamado Análisis en Componentes Principales o ACP23 para proyectar primero el espacio de descriptores en un espacio con 50 dimensiones, y así facilitar el trabajo del algoritmo t-SNE. En la práctica utilizamos la implementación de dicho algoritmo presente en la librería de Python scikit-learn24, estableciendo una perplejidad igual a 70 y fijando los demás parámetros a sus valores por defecto
Clasificación y SHAP-values
Para poder analizar las dimensiones más importantes que caracterizan cada clúster, se procedió a entrenar un modelo de Random Forest25, que a partir de los objetos descritos en el espacio de descriptores químicos predice el clúster al cual el objeto pertenece. En la práctica se utilizó la implementación del algoritmo de Random Forest disponible en la librería scikit-learn de Python24, y se fijó a 1,000 el número de árboles de clasificación, con el fin de tener una mejor predicción y contrarrestar posibles problemas de sobre entrenamiento, mientras que los demás parámetros fueron establecidos a sus valores estándar. Se evaluó la calidad de este modelo por medio de una estrategia de validación cruzada estratificada y repetida, el conjunto de datos fue dividido en 10 subconjuntos de mismo tamaño y con la misma proporción de objetos de cada clúster, cada uno de ellos se empleó a su vez como conjunto de validación, mientras que los restantes subconjuntos se emplearon como conjunto de entrenamiento; este procedimiento se repitió un total de 5 veces, lo cual generó un total de 50 estimaciones de la calidad en diferentes subconjuntos de datos. En este trabajo utilizamos la medida 𝐴𝑐𝑐𝑢𝑟𝑎𝑐𝑦, que contabiliza la proporción de objetos correctamente, para evaluar la calidad del modelo.
Finalmente, para poder analizar la importancia de cada descripción en la clasificación de cada clúster, procedimos a calcular las llamadas SHAP-values26, que permiten cuantificar el grado de importancia de cada descriptor en la tarea predictiva de un modelo dado. En la práctica, dado que empleamos un modelo de Random Forest, basado en arboles de clasificación, empleamos el algoritmo TreeSHAP con el fin de estimar dichos valores, de manera más rápida.
RESULTADOS Y DISCUSIÓN
Como se puede observar en la figura 2, el número de iteraciones Nbiter = 10,000 fue suficiente para que los 100 modelos individuales llegaran a converger hacia niveles similares en términos de SAE, entorno a valores cercanos a 90,000. Por otra parte, en la misma figura podemos apreciar que la fusión de modelos produjo un modelo con una SAE muy inferior, por debajo de 80.000. Esto sugiere que el modelo fusión describe de manera más precisa los datos. Por otra parte, el modelo de fusión formado por las 13 medianas más importantes de los 100 modelos independientes, comenzó directamente con un valor muy bajo de SAE (dado que fue inicializado con las mejores medianas de los modelos independientes finales), y solo optimizo ligeramente su SAE. Después de 10,000 iteraciones, el modelo fusión conservó sus 13 medianas, y los clústeres asociados lograron capturar un número bastante variable de objetos que van de 22 objetos para el clúster más pequeño (clúster 12), a 318 objetos para el clúster más grande (clúster 3).
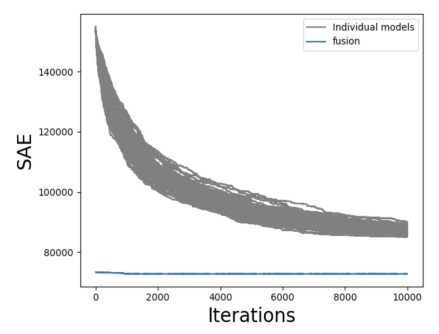
Figura 3: Evolución de la suma de errores absolutos (SAE) de 100 modelos independientes generados por SubCMedians (gris) y evolución del modelo de subspace clustering de fusión (azul).
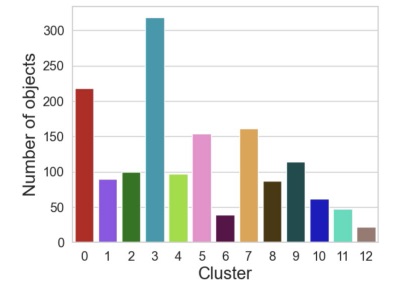
Figura 4: Cantidad de objetos pertenecientes a cada clúster en el modelo de subspace clustering de fusión. El número de objetos por clúster varía de manera importante (de cerca de 20 objetos para el clúster a más de 300 para el clúster más grande).
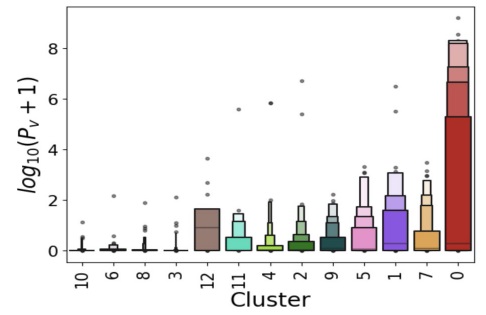
La representación en 2D generada por el algoritmo t-SNE muestra una clara cohesión de los clústeres formados por SubCMedians, como puede apreciarse en la figura 4. Por otra parte, en esta figura se evidencia que algunos clústeres (por ejemplo el clúster 0) poseen un mayor número de moléculas con volatilidad alta (log10 (Pv + 1) > 5), las cuales se ven representadas con círculos de mayor diámetro en la imagen 4. Esta observación se ve corroborada por el boxenplot representado en la figura 5 y la tabla ilustrada en la figura 6, que representa la distribución de la volatilidad en escala logarítmica (log10 (Pv + 1)) de las moleculas contenidas en cada clúster. Los clústeres 0, 7, 5 y 1 poseen claramente más estructuras moleculares con volatilidad elevada, mientras que los clústeres 3, 8, 6 y 10 están claramente poblados por moléculas con volatilidad baja.
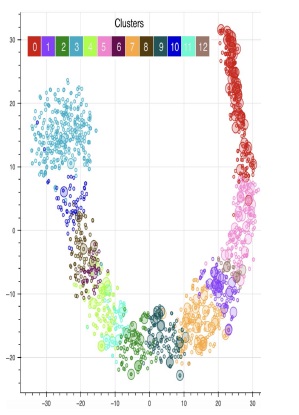
Figura 5: Proyección 2D generada por el método t-SNE de cada objeto. El color de cada punto evidencia el clúster de pertenencia del objeto representado. Los puntos grandes representan moléculas volátiles.
Figura 7: Cantidad de moléculas de cada clase de volatilidad, i.e., alta (high), baja (low) o sin datos (NaN), para cada uno de los cluster.
El modelo de Random Forest que fue entrenado para poder clasificar las moléculas en función de sus clústeres a partir de descriptores químicos, ha demostrado buenos valores de Accuracy (cuya media sobrepasa 0.93), como puede evidenciarse en el boxplot representado en la figura 8.
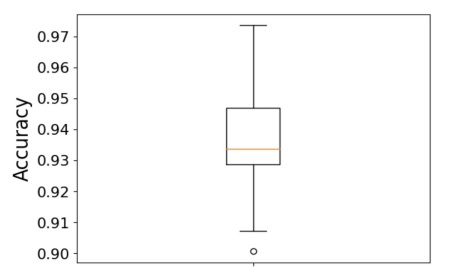
Figura 8: Distribución de la medida de calidad (Accuracy) del modelo Random Forest que tiene por objetivo clasificar las moléculas en función de su clúster de pertenencia
Esto demuestra una vez más la cohesión de los clústeres generados pro SubCMedians, lo cual hace que la tarea de clasificación asociada sea relativamente sencilla. Este modelo no se apoya solo en unos cuantos descriptores y tiene más bien tendencia a emplear los diferentes descriptores con una importancia similar como puede evidenciarse en el gráfico de barras representado en la figura 9, que ilustra la medida de importancia (Feature Importance) asociada a los 20 descriptores más importantes para el modelo de Random Forest en la tarea de clasificación. La suma de las medidas de Feature Importance atribuidas a cada descriptor es igual a uno, y por ende, de ser igualmente importantes, los 126 descriptores del conjunto de datos deberían exhibir un Feature Importance igual a 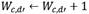. Sin embargo, es importante notar que la importancia de cada descriptor para clasificar las moléculas depende de cada clúster.
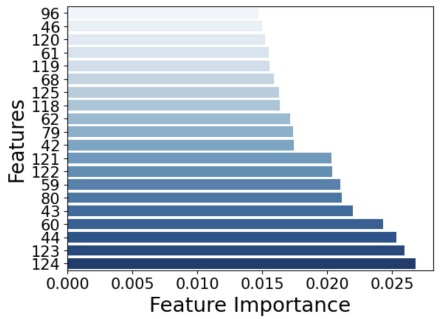
Figura 9: Veinte descriptores más importantes para el modelo de Random Forest y sus valores de Feature Importance correspondientes.
En efecto, por ejemplo, el clúster 0, enriquecido en moléculas con alta volatilidad (Tabla 1), están caracterizado por los descriptores 39, 40, 41, 42, 43, 44, 45, 46 y 60 (los valores bajos en estos descriptores tienen a caracterizar los objetos que pertenecen en este clúster). Mientras que el clúster 3, enriquecido en moléculas con baja o nula volatilidad, esta caracterizado por los descriptores 117, 118, 119, 120, 121, 122, 124 y 125 (los valores altos en estos descriptores tienden a caracterizar los objetos que pertenecen en este clúster).
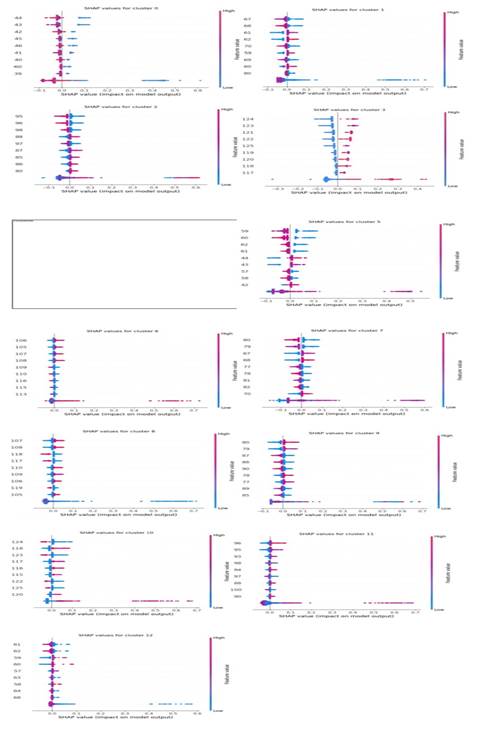
Figura 10: SHAP-values (importancia) de los nueve descriptores más importantes la predicción de cada uno de los clústeres por parte del modelo de Random Forest.
Dada la gran heterogeneidad de las estructuras moleculares (Tabla 1), los grupos clasificados tienen ciertas tendencias con características genéricas, por ejemplo, en el grupo 0, se encuentran compuestos de hidrocarburos halogenados, fenoles, ácidos y derivados carboxílicos, algunas sales orgánicas, alcoholes y algunos nitrogenados con pesos moleculares entre 70 y 400 g/mol. En el grupo 1, se encuentran compuestos orgánicos clorados, nitrogenados, herbicidas, ácidos, ésteres y otros compuestos, sus pesos moleculares varían entre 30 y 500 g/mol. En el grupo 2, se encuentran carbamatos, organofosforados, piretroides y otros, con pesos moleculares entre 170 y 500 g/mol. En el grupo tres, Piretroides, herbicidas, fungicidas con pesos moleculares entre 250 y 550 g/mol. Los otros grupos también son clasificados casi del mismo modo.
CONCLUSIONES
En este estudio se aplicó SubCMedians, un algoritmo de subspace clustering para analizar un conjunto de datos de estructuras moleculares aplicadas en sustancias utilizadas en la agricultura como pesticidas. El modelo de clustering obtenido consta de 13 clústeres (Tabla 1), cada uno de ellos posee diferentes tipos de moléculas con distintas propiedades. Por ejemplo, se ha podido evidenciar que algunos de estos clústeres contenían moléculas con volatilidad más elevada, mientras que otros solo contenían moléculas con baja volatilidad. Por otra parte, cada clúster está caracterizado por un subconjunto de descriptores químicos característicos. Se ha intentado dar una explicación de los clústers desde un punto de vista de la estructura molecular y su composición, sin embargo, dada la gran heterogeneidad de las mismas, los grupos clasificados muestran una cierta tendencia de carácter genérico a agruparse en tipos de compuestos y estructuras con características similares. Finalmente, los resultados del presente trabajo, abren la posibilidad de establecer modelos cuantitativos de relaciones estructura-propiedad a objeto de predecir el valor de la presión de vapor de los compuestos en cada grupo subclasificado mediante modelos matemático-estadísticos o de redes neuronales para todos aquellos compuestos que no cuentan con datos experimentales.
