Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Fides et Ratio - Revista de Difusión cultural y científica de la Universidad La Salle en Bolivia
versión On-line ISSN 2071-081X
Fides Et Ratio v.7 n.7 La Paz mar. 2014
ARTICULOS ORIGINALES
TÓPICOS DE INFERENCIA ESTADÍSTICA: EL MÉTODO INDUCTIVO Y EL PROBLEMA DEL TAMAÑO DE LA MUESTRA
TOPICS OF STATISTICAL INFERENCE: INDUCTIVE METHOD AND THE PROBLEM OF SAMPLE SIZE
Bruno E. Vargas Biesuz
Instituto de Investigación en Ciencias Económicas y Financieras Universidad La Salle - Bolivia
bruvarbi@gmail.com
Recibido: 10/08/2013
Aceptado: 03/02/2014
RESUMEN
El artículo explica lo que se debe entender como "Método Inductivo" de investigación y cómo se debe calcular el tamaño de una muestra, cuando se usa este método.
PALABRAS CLAVE Inferencia, Promedio, Población, muestra aleatoria, muestra, Varinaza.
ABSTRACT
This paper deals about the meaning of the "Inference" in science and the way to calcúlate the size of the sample.
KEYWORDS Inference, Mean, Populations, Random Sampling, Sample, Variance.
I. INTRODUCCIÓN
La estadística moderna se aplica actualmente en una muy grande gama de ciencias como "un método científico de análisis" [1] Posiblemente sea el método preferido para la comprobación de la validez de los nuevos conocimientos, dado su rigor metodológico y su sustento matemático. Esta ciencia, puede ser muy compleja en su marco teórico que está basado principalmente en modelos matemáticos, sin embargo puede ser bastante accesible en su aplicación práctica. En este contexto, uno de los problemas que tienen quienes tratan de aplicar la estadística inferencial en las investigaciones, es la determinación del tamaño de la muestra. Este trabajo aborda este problema y trata precisamente de ser una guía para quienes utilizan este método de análisis científico para sus indagaciones y deben resolver el asunto concerniente al tamaño de la muestra que se debe tomar, a partir de la cual se realizarán las inferencias y las pruebas de hipótesis planteadas. Sin embargo antes de analizar el problema planteado, considero necesario explicar en qué consiste el método inductivo o inferencial que usa la estadística.
II. OBJETIVOS
El objetivo del presente artículo, es la revisión del tema específico que se presenta a quienes realizan investigación científica, usando el método inductivo o inferencial y presentar respuestas prácticas, en términos de expresiones matemáticas o fórmulas, para calcular el tamaño de una muestra aleatoria.
III. POBLACIÓN, MUESTRA Y ERROR
La esencia de la estadística tiene que ver con el hecho de que los investigadores tratan de conocer las características de una determinada población o colectivo. La población "es el conjunto total de objetos o personas que van a estudiarse" [2] y, puede ser de cualquier tamaño. Por ejemplo un ingeniero industrial estará interesado en estudiar las fábricas de textiles de todo el país y, obtener ciertas características de este colectivo como ser: cuántos trabajadores en promedio están contratados por fábrica, el monto promedio de inversiones en bienes de capital por trabajador, la proporción de hombres o mujeres que trabajan en la industria, etc. A un psicólogo le interesaría estudiar el comportamiento de los adolecentes de una ciudad y, analizar ciertas variables como: el número de horas promedio que miran televisión, el número de libros que en promedio leen por año o cualquier otra característica.
Lo sorprendente del caso es que, la técnica estadística permite obtener las características buscadas (p.e. promedios), sin necesidad de estudiar a toda la población. ¡Será suficiente obtener y estudiar una pequeña parte de la población y a partir del estudio de esa pequeña parte, la cual se llama muestra, se obtienen aproximadamente los mismos resultados;
Esta técnica estadística se usa por varias razones, entre las más importantes:
o Es menos costoso estudiar una muestra que a toda la población.
o Lleva menos tiempo estudiar una muestra que a toda la población.
Debe quedar claro sin embargo que los resultados o características que se obtengan de la muestra, pueden ser iguales a los de la población o bastante aproximados.
Esto nos lleva al concepto de "error" estadístico. Es decir esta técnica científica, admite que la característica de la muestra (p.e. promedio muestral X), es igual o se aproxima bastante a la característica de la población (p.e. promedio poblacional ![]() ). En otras palabras: el promedio de la población (
). En otras palabras: el promedio de la población (![]() ), es igual al promedio de la muestra (X), más o menos cierto error:
), es igual al promedio de la muestra (X), más o menos cierto error: ![]()
![]()
El asunto fundamental aquí es, ¿qué tan pequeño es ese error?, ¿Qué certeza se tiene de estar cerca del dato correcto? Las respuestas a estas preguntas dependen de que la muestra haya sido obtenida de forma aleatoria, es decir por sorteo, donde todos los elementos o componentes de la población hayan tenido la misma posibilidad de haber sido elegidos y de un tamaño adecuado de muestra, problema que trata de resolver este artículo.
III. 1 INDUCCIÓN Y DEDUCCIÓN
Una vez explicados los conceptos de población, muestra y error, pasamos a explicar el significado y esencia del método inductivo o inferencial que usa la estadística en su análisis.
El método o razonamiento inductivo implica la determinación de las características generales de toda una población, a partir del estudio de lo específico, es decir de la muestra. Muchas veces se explica esto diciendo que el método inductivo va de lo particular a lo general, definición poco clara si no se analizan antes los conceptos de población, muestra y error.
III.2 CALCULO DEL TAMAÑO DE MUESTRA
DE AQUI PA DELANTE FALTA
Generalmente, los motivos que llevan a usar el método inductivo o inferencial en las investigaciones y por lo yanto a la obtención de una muestra, son estimar la media o promedio poblacional (![]() ), la deviación estándar poblacional (
), la deviación estándar poblacional (![]() ) o la proporción poblacional (
) o la proporción poblacional (![]() ) . En toda estimación de estos parámetros poblacionales, el investigador se permite o tolera un error máximo "
) . En toda estimación de estos parámetros poblacionales, el investigador se permite o tolera un error máximo " ![]() " que es previamente estipulado. Además se debe establecer la confianza de que el error no supere esa cantidad "
" que es previamente estipulado. Además se debe establecer la confianza de que el error no supere esa cantidad "![]() ", lo cual será denotado por (1 -
", lo cual será denotado por (1 -![]() ), diferencia que llamaremos "coeficiente de confianza".
), diferencia que llamaremos "coeficiente de confianza".
m.2.1 TAMAÑO DE MUESTRA PARA ESTIMAR LA MEDIA POBLACIONAL (![]() ), CUANDO SE CONOCE LA DESVIACIÓN ESTÁNDAR (
), CUANDO SE CONOCE LA DESVIACIÓN ESTÁNDAR (![]() ).
).
Lo que se busca es que el tamaño de la muestra "n", sea tal que:
![]()
Según la desigualdad de Shebyshev:

Según el Teorema Central del Límite:
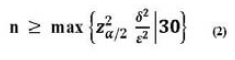
Ejemplo: Se quiere estimar (![]() ), promedio poblacional mediante el promedio muestral (X), con un error
), promedio poblacional mediante el promedio muestral (X), con un error ![]() = 0,01 y un coeficiente de confianza (1 -
= 0,01 y un coeficiente de confianza (1 -![]() ) = 0,9. Se conoce que
) = 0,9. Se conoce que ![]() 2
2
De aquí: ![]()
Z 0,05 = 1,64 según tabla de probabilidad normal estándar
Según la relación (1):
![]()
Según la relación (2):

Nótese una significativa diferencia entre los resultados de las relaciones (1) y (2), por lo que es más recomendable la última fórmula.
III.2.2 TAMAÑO DE LA MUESTRA PARA ESTIMAR LA MEDIA POBLACIONAL Oí), CUANDO NO SE CONOCE LA DESVIACIÓN ESTÁNDAR (![]() )
)
En este caso existen dos posibilidades de cálculo.
4.2.1 Se estima la Desviación Estándar (![]() ) con la fórmula empírica :
) con la fórmula empírica :
![]()
Por(l):
Donde el "Rango" o recorrido de la variable estudiada es la diferencia entre el valor máximo y el valor mínimo.
Rango = (X max - X min)
Luego se emplean las relaciones (1) o (2)
Ejemplo: En una fábrica de jabón en polvo, se quiere estimar la producción semanal media (u), mediante la media muestral (X), deseándose que | X - ![]() | < 4 Ton. Hay razones para creer que la producción semanal oscila entre 340 y 420 Ton. Calcule el tamaño de la muestra para un coeficiente de confianza (1 -
| < 4 Ton. Hay razones para creer que la producción semanal oscila entre 340 y 420 Ton. Calcule el tamaño de la muestra para un coeficiente de confianza (1 -![]() ) = 0,95 Datos:
) = 0,95 Datos:
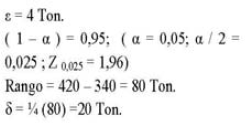
Por (1):
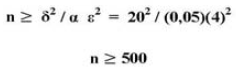
Por (2):
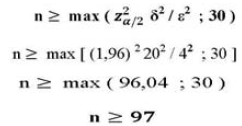
En el segundo caso, se sustituye " ![]() " (desviación estándar poblacional), por "s" (desviación standar muestral o error standar), en las fórmulas (1) y (2).
" (desviación estándar poblacional), por "s" (desviación standar muestral o error standar), en las fórmulas (1) y (2).
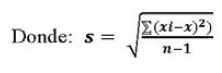
Por tanto, las nuevas relaciones son:
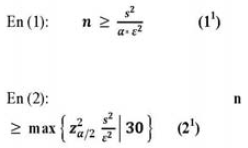
Sin embargo, las fórmulas (I1) y (21) contienen una contradicción, ya que para el cálculo de de "s2", se necesita saber el valor de "n", es decir, se necesita haber tomado una muestra, cuyo valor aún no se sabe y es precisamente lo que se trata de calcular.
Esta contradicción se salva calculando "S2" a partir de una "muestra piloto", cuyo tamaño podría ser treinta (n = 30). Luego se sigue el siguiente criterio de decisión:
a) Se calcula el valor de ni, si n1 ![]() 30 se acepta el valor de n=30
30 se acepta el valor de n=30
b) Si ni > 30 se amplía el tamaño de la muestra, se calcula el nuevo valor de "s" y con este se determina n2, si n2![]() n1 se acepta n1
n1 se acepta n1
c) Si n2 > ni se amplía la muestra, calculando nuevamente "s", y así sucesivamente.+
III.2.3 TAMAÑO DE LA MUESTRA PARA ESTIMAR LA VARIANZA POBLACIONAL ( ![]() 2) Se pretende calcular el tamaño de la muestra "n" de modo que:
2) Se pretende calcular el tamaño de la muestra "n" de modo que:
![]()
Usando la desigualdad de Chebyshev se obtiene:
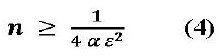
Empleando el Teorema Central del Límite, se obtiene:

La primera fórmula (4), da generalmente un valor demasiado grande, en cambio la formula (5). gracias a la aproximación del teorema Central del Límite, da generalmente un valor de "n" bastante menor, por lo que es preferida.
Ejemplo: Se quiere estimar "![]() " mediante "P" con
" mediante "P" con ![]() = 0,02 y (1 -
= 0,02 y (1 - ![]() )= 0,95, de donde
)= 0,95, de donde ![]() =0,05;
=0,05; ![]() /2 = 0,025. Z 0,025 = 1,96
/2 = 0,025. Z 0,025 = 1,96

III.2.5 FORMULA DE MUNCH Y ANGELES.
[3] Otra posibilidad para estimar el tamaño de muestra para proporciones o porcentajes de población, cuando la población (N) es muy grande y la variable aleatoria estudiada es binomial o dicotómica, es la fórmula de Lourdes Munch y Ernesto Angeles:
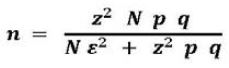
Donde:
Z = valor estándar de la distribución probabilística normal para el nivel de confianza establecido (si 95 % ? z = 1,96)
![]() = error probable
= error probable
p = probabilidad de éxito
q = probabilidad de fracaso
N = Población o universo
n = tamaño de la muestra
Si no se cuenta con información sobre la probabilidad de éxito o fracaso, se recomienda usar p = q = 0,5 Por otra parte, el error (![]() ) máximo recomendable debe ser 0.1
) máximo recomendable debe ser 0.1
Si la población es finita, se recomienda usar el Muestreo Aleatorio Simple y la siguiente fórmula:
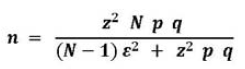
BIBLIOGRAFÍA
[1] Thomas H. Wonnacott & Ronald J. Wonnacott. (1979). Fundamentos de Estadística Para Administración y Economía. Editorial Limusa México [ Links ]
[2] Thomas H. Wonnacott & Ronald J. Wonnacott. (1991). Estadística Básica Práctica. Editorial Limusa México [ Links ]
[3] www.monografias.com [ Links ]
VI AGRADECIMIENTO:
El autor agradece las explicaciones, aclaraciones y cooperación brindadas en su momento, por el Ingeniero Luís Crespo Ostria, destacado académico, a quien tuvimos el privilegio de contar en la planta docente de la Universidad La Salle, por lo que el presente artículo está dedicado a su memoria.
Asimismo, se agradece al Licenciado Dindo Valdez en la atención recibida en la revisión del artículo.













